Dynamic Causal Model for Steady State Responses Rosalyn

Dynamic Causal Model for Steady State Responses Rosalyn Moran Wellcome Trust Centre for Neuroimaging

DCM for Steady State Responses A dynamic causal model (DCM) of steady-state responses in electrophysiological data is summarised in terms of their cross-spectral density. Where These spectral data-features are generated by a biologically plausible, neural-mass model of coupled electromagnetic sources; where each source comprises three sub-populations. Under linearity and stationarity assumptions, the model’s biophysical parameters (e. g. , post-synaptic receptor density and time constants) prescribe the cross-spectral density of responses measured directly (e. g. , local field potentials) or indirectly through some lead-field (e. g. , electroencephalographic and magnetoencephalographic data). Inversion of the ensuing DCM provides conditional probabilities on the synaptic parameters of intrinsic and extrinsic connections in the underlying neuronal network

Overview 1. Data Features 2. The Generative Model in DCMs for Steady-State Responses - neural mass model 3. Bayesian Inversion: Parameter Estimates and Model Comparison 4. Example. DCM for Steady State Responses: § Glutamate with Microdialysis validation § Predicting Anaesthetic Depth

Overview 1. Data Features 2. The Generative Model in DCMs for Steady-State Responses - neural mass model 3. Bayesian Inversion: Parameter Estimates and Model Comparison 4. Example. DCM for Steady State Responses: § Glutamate with Microdialysis validation § Predicting Anaesthetic Depth

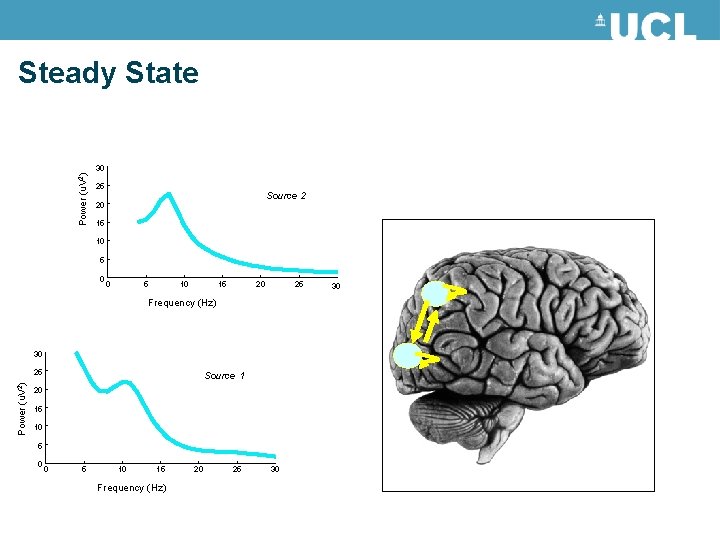
Steady State Statistically: A “Wide Sense Stationary” signal has 1 st and 2 nd moments that do not vary with respect to time Dynamically: A system in steady state has settled to some equilibrium after a transient Data Feature: Quasi-stationary signals that underlie: Spectral Densities in the Frequency Domain

Steady State Power (u. V 2) 30 25 Source 2 20 15 10 5 0 0 5 10 15 20 25 Frequency (Hz) 30 Power (u. V 2) 25 Source 1 20 15 10 5 0 0 5 10 15 Frequency (Hz) 20 25 30 30

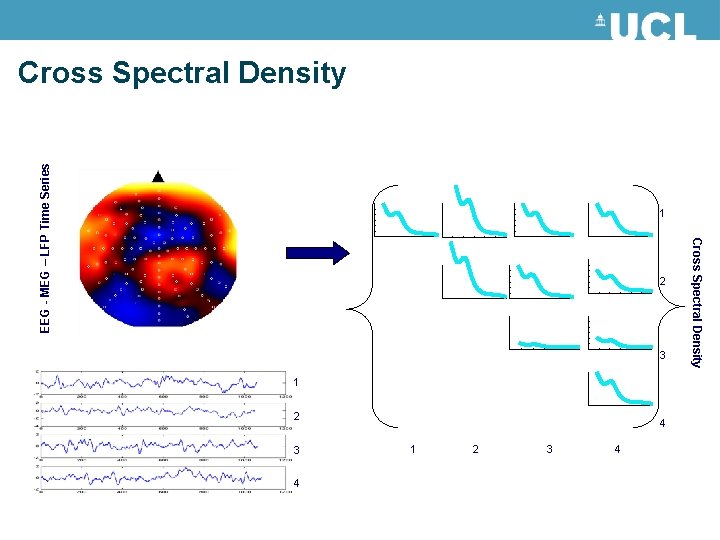
EEG - MEG – LFP Time Series Cross Spectral Density 1 3 1 2 3 4 4 1 2 3 4 Cross Spectral Density 2

Cross Spectral Density Vector Auto-regression a p-order model: Linear prediction formulas that attempt to predict an output y[n] of a system based on the previous outputs Resulting in a matrices for c Channels Cross Spectral Density for channels i, j at frequencies

Overview 1. Data Features 2. The Generative Model in DCMs for Steady-State Responses - neural mass model 3. Bayesian Inversion: Parameter Estimates and Model Comparison 4. Example. DCM for Steady State Responses: § Glutamate with Microdialysis validation § Predicting Anaesthetic Depth

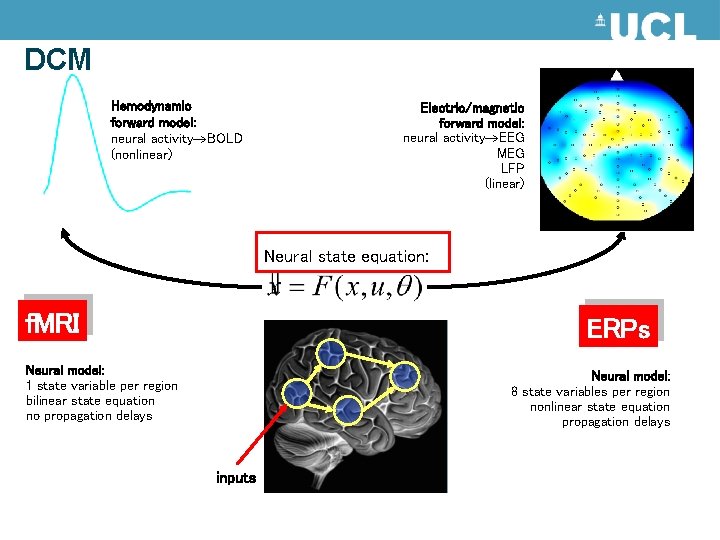
DCM Hemodynamic forward model: neural activity BOLD (nonlinear) Electric/magnetic forward model: neural activity EEG MEG LFP (linear) Neural state equation: f. MRI ERPs Neural model: 1 state variable per region bilinear state equation no propagation delays Neural model: 8 state variables per region nonlinear state equation propagation delays inputs

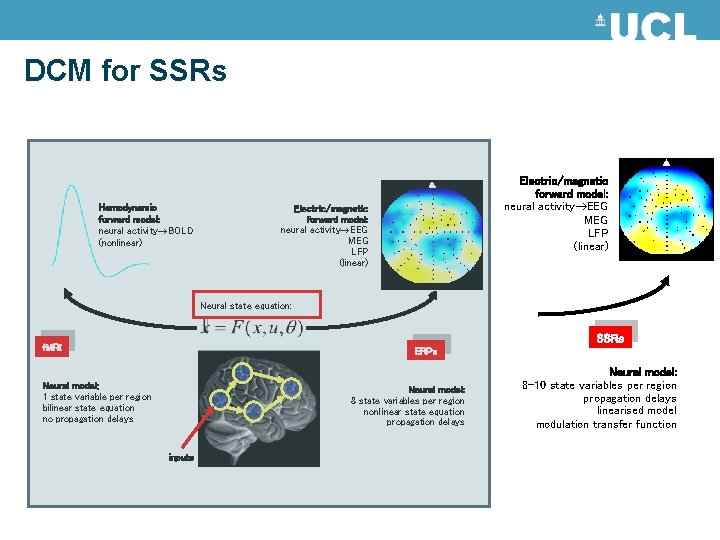
DCM for SSRs Hemodynamic forward model: neural activity BOLD (nonlinear) Electric/magnetic forward model: neural activity EEG MEG LFP (linear) Neural state equation: SSRs f. MRI ERPs Neural model: 1 state variable per region bilinear state equation no propagation delays Neural model: 8 state variables per region nonlinear state equation propagation delays inputs Neural model: 8 -10 state variables per region propagation delays linearised model modulation transfer function

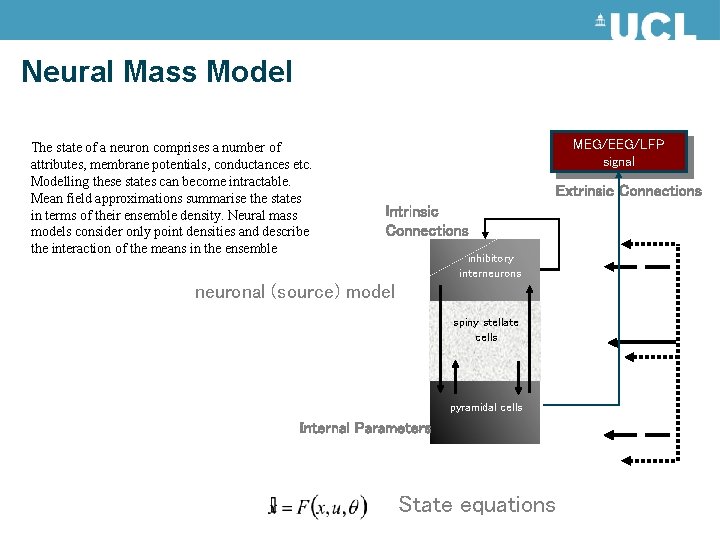
Neural Mass Model The state of a neuron comprises a number of attributes, membrane potentials, conductances etc. Modelling these states can become intractable. Mean field approximations summarise the states in terms of their ensemble density. Neural mass models consider only point densities and describe the interaction of the means in the ensemble MEG/EEG/LFP signal Extrinsic Connections Intrinsic Connections inhibitory interneurons neuronal (source) model spiny stellate cells pyramidal cells Internal Parameters State equations

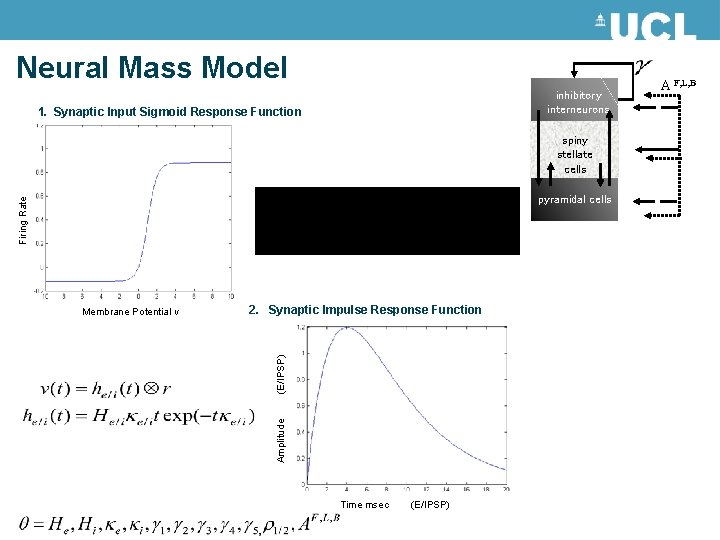
Neural Mass Model inhibitory interneurons 1. Synaptic Input Sigmoid Response Function spiny stellate cells Firing Rate pyramidal cells (E/IPSP) 2. Synaptic Impulse Response Function Amplitude Membrane Potential v Time msec (E/IPSP) A F, L, B

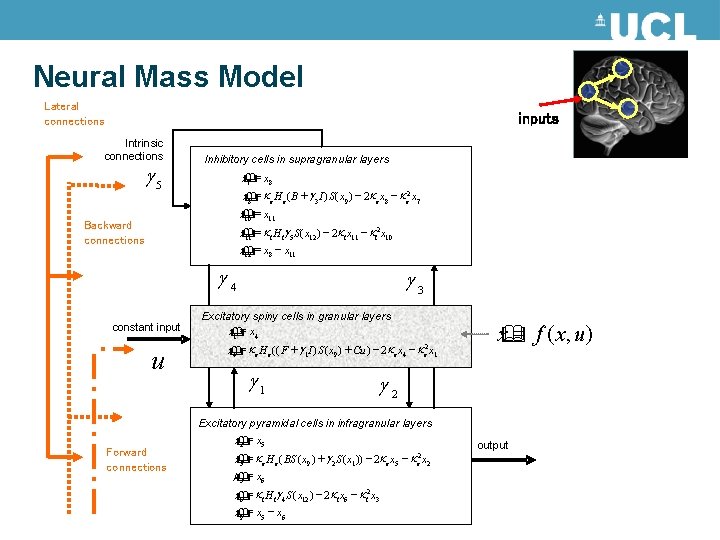
Neural Mass Model Lateral connections inputs Intrinsic connections g 5 Inhibitory cells in supragranular layers = x 8 x& 7 = k e H e ( B + g 3 I ) S ( x 9 ) - 2 k e x 8 - k e 2 x 7 x& 8 = x 11 x& 10 Backward connections = k i H ig 5 S ( x 12 ) - 2 k i x 11 - k i 2 x 10 x& 11 = x 8 - x 11 x& 12 g 4 constant input u Forward connections g 3 Excitatory spiny cells in granular layers == x& x& 11 xx 44 =k x& x& 44 = k g kk He e((( F 1 s+( x 91 I-) Sa() x+9 )u + ) -Cu 2 ) e-x 42 -e xe 42 x-1 ee. H g 1 g k k 2 e x 1 = f ( x, u ) x& g 2 Excitatory pyramidal cells in infragranular layers = x 5 x& 2 = k e H e ( BS ( x 9 ) + g 2 S ( x 1 )) - 2 k e x 5 - k e 2 x& 5 m& = x 6 3 = k i H ig 4 S ( x 12 ) - 2 k i x 6 - k i 2 x 3 x& 6 = x 5 - x 6 x& 9 output

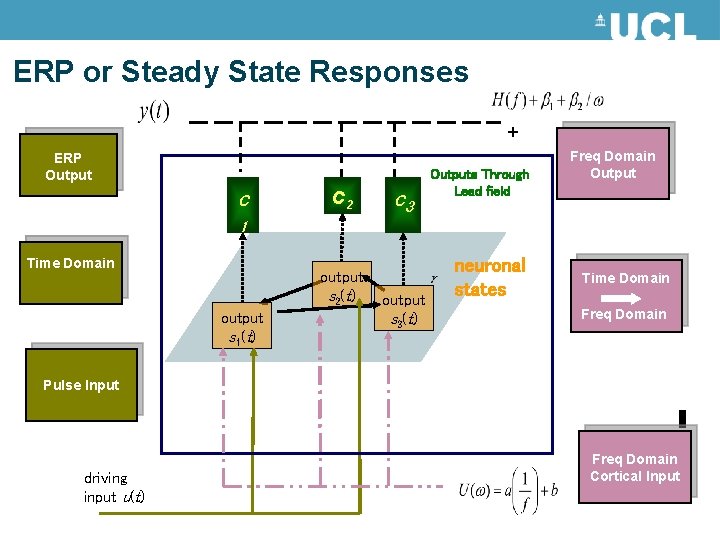
ERP or Steady State Responses + ERP Output c c 2 c 3 Outputs Through Lead field Freq Domain Output 1 Time Domain output s 2(t) output s 1(t) output s 3(t) neuronal states Time Domain Freq Domain Pulse Input driving input u(t) Freq Domain Cortical Input

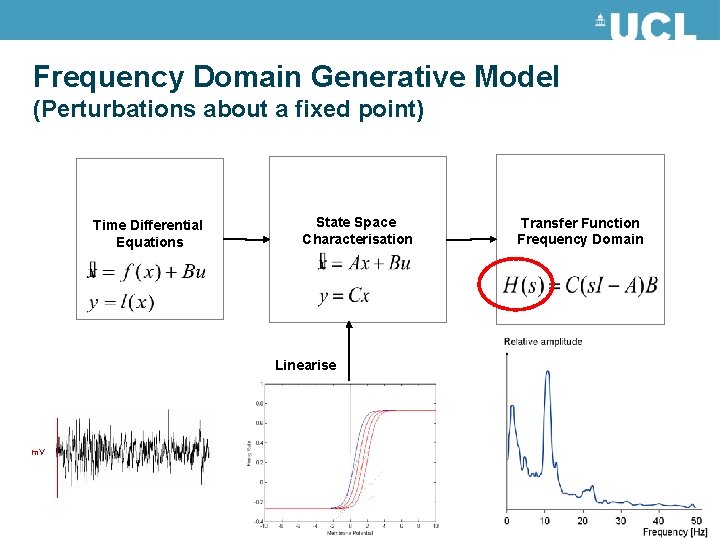
Frequency Domain Generative Model (Perturbations about a fixed point) Time Differential Equations State Space Characterisation Linearise m. V Transfer Function Frequency Domain

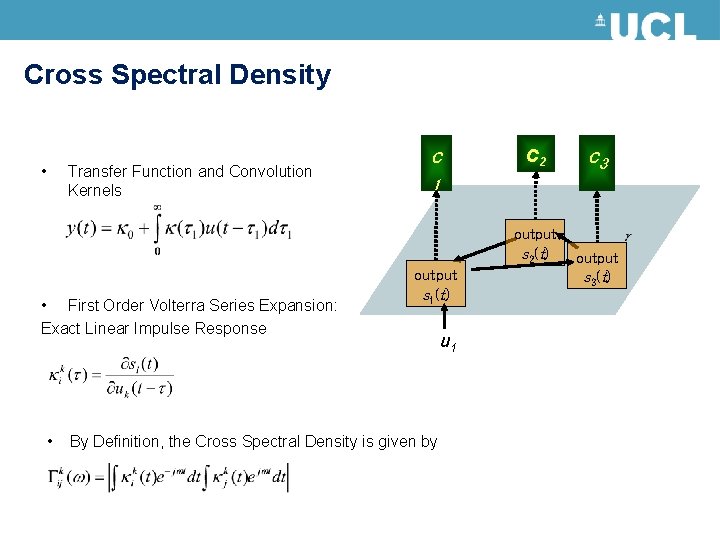
Cross Spectral Density • Transfer Function and Convolution Kernels c c 2 1 output s 2(t) • First Order Volterra Series Expansion: Exact Linear Impulse Response • c 3 output s 1(t) By Definition, the Cross Spectral Density is given by u 1 output s 3(t)

Overview 1. Data Features 2. The Generative Model in DCMs for Steady-State Responses - a family of neural mass model 3. Bayesian Inversion: Parameter Estimates and Model Comparison 4. Example. DCM for Steady State Responses: § Glutamate with Microdialysis validation § Predicting Anaesthetic Depth

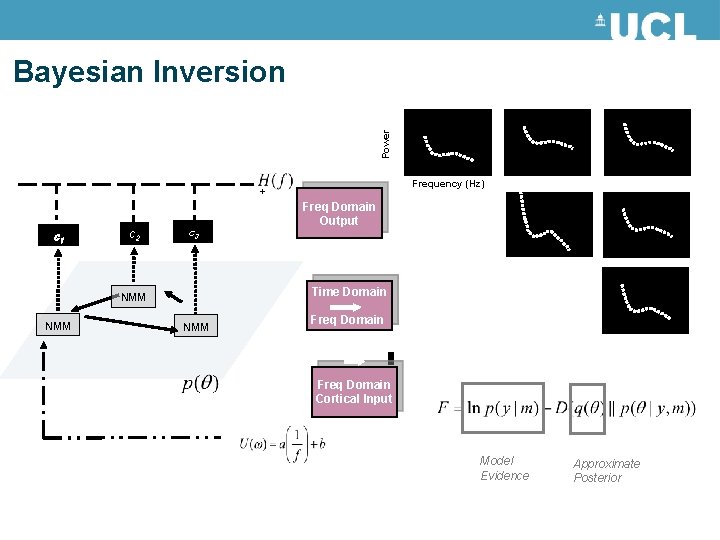
Power Bayesian Inversion Frequency (Hz) + c 1 c 2 c 3 Time Domain NMM Freq Domain Output NMM Freq Domain Cortical Input Model Evidence Approximate Posterior

Inversion Neural Parameters Observer function Define likelihood model Specify priors Inference on models Invert model Inference on parameters Make inferences

Overview 1. Data Features 2. The Generative Model in DCMs for Steady-State Responses - a family of neural mass model 3. Bayesian Inversion: Parameter Estimates and Model Comparison 4. Example. DCM for Steady State Responses: § Glutamate with Microdialysis validation § Predicting Anaesthetic Depth

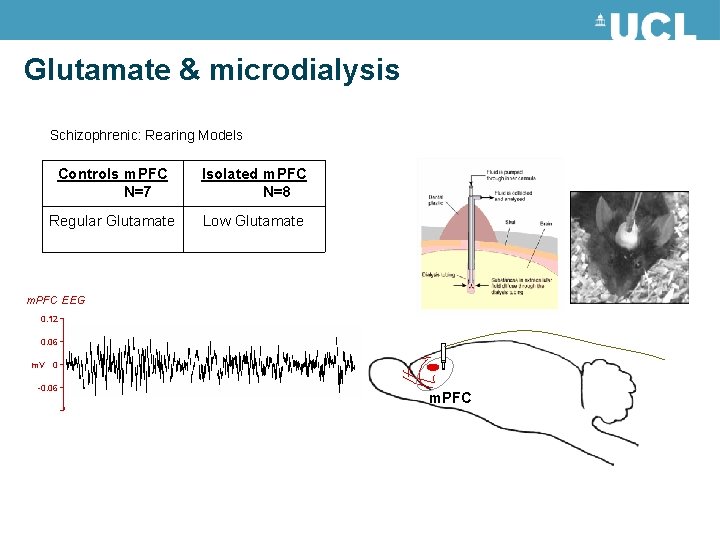
Glutamate & microdialysis Schizophrenic: Rearing Models Controls m. PFC N=7 Isolated m. PFC N=8 Regular Glutamate Low Glutamate m. PFC EEG 0. 12 0. 06 m. V 0 -0. 06 m. PFC

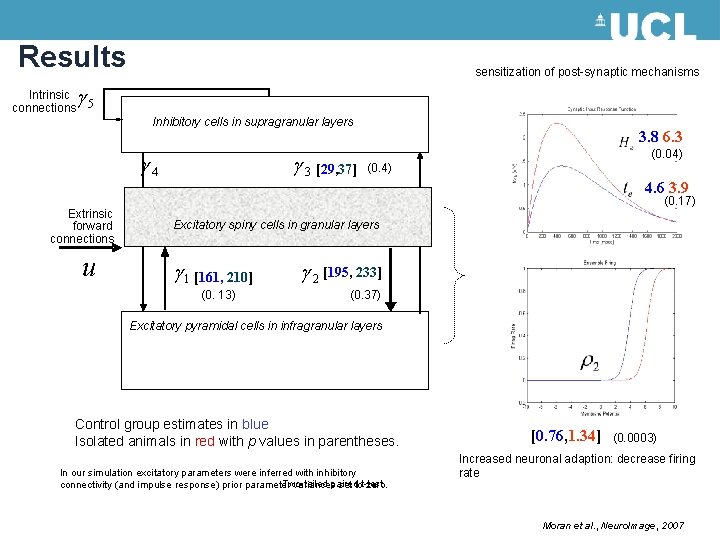
Hypotheses • Main findings from microdialysis: – reduction in prefrontal glutamate levels of isolated group → sensitization of post-synaptic mechanisms (e. g. upregulation) • Model parameters should reflect – amplitude of synaptic kernels – coupling parameters of glutamatergic connections – neuronal adaptation (i. e. , 2)

Results sensitization of post-synaptic mechanisms g Intrinsic connections 5 Inhibitory cells in supragranular layers g 3 [29, 37] g 4 Extrinsic forward connections u [3. 8, 6. 3] (0. 04) (0. 4) [4. 6, 3. 9] (0. 17) Excitatory spiny cells in granular layers g 1 [161, 210] (0. 13) g 2 [195, 233] (0. 37) Excitatory pyramidal cells in infragranular layers Control group estimates in blue Isolated animals in red with p values in parentheses. In our simulation excitatory parameters were inferred with inhibitory Two-tailed paired connectivity (and impulse response) prior parameter variances set tot-test zero. [0. 76, 1. 34] (0. 0003) Increased neuronal adaption: decrease firing rate Moran et al. , Neuro. Image, 2007

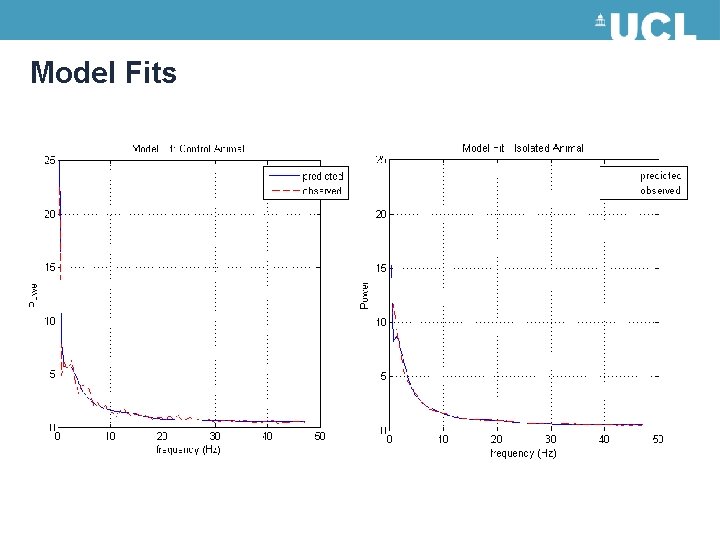
Model Fits

Overview 1. Data Features 2. The Generative Model in DCMs for Steady-State Responses - a family of neural mass model 3. Bayesian Inversion: Parameter Estimates and Model Comparison 4. Example. DCM for Steady State Responses: § Glutamate with Microdialysis validation § Predicting Anaesthetic Depth

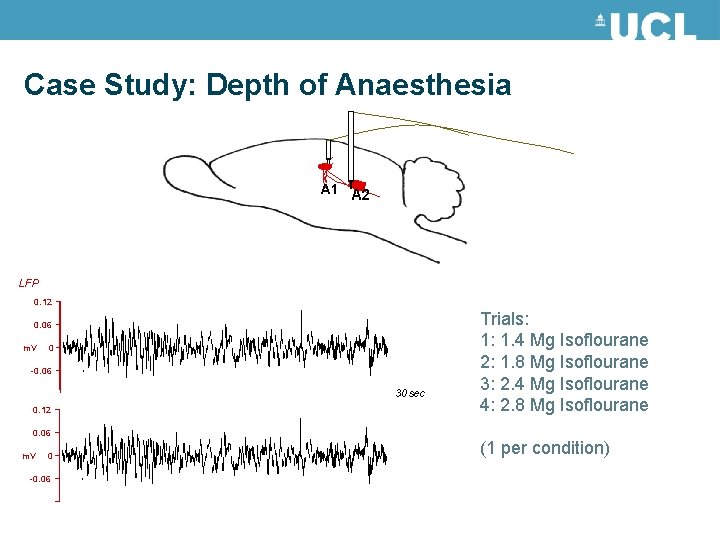
Case Study: Depth of Anaesthesia A 1 A 2 LFP 0. 12 0. 06 m. V 0 -0. 06 30 sec 0. 12 Trials: 1: 1. 4 Mg Isoflourane 2: 1. 8 Mg Isoflourane 3: 2. 4 Mg Isoflourane 4: 2. 8 Mg Isoflourane 0. 06 m. V 0 -0. 06 (1 per condition)

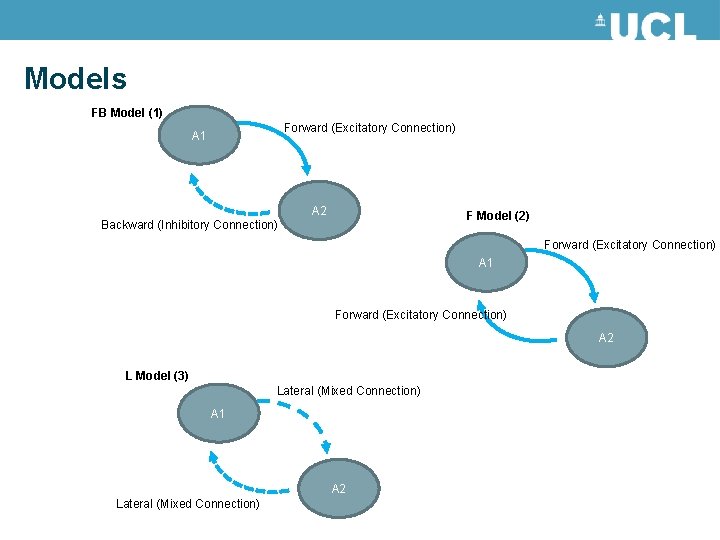
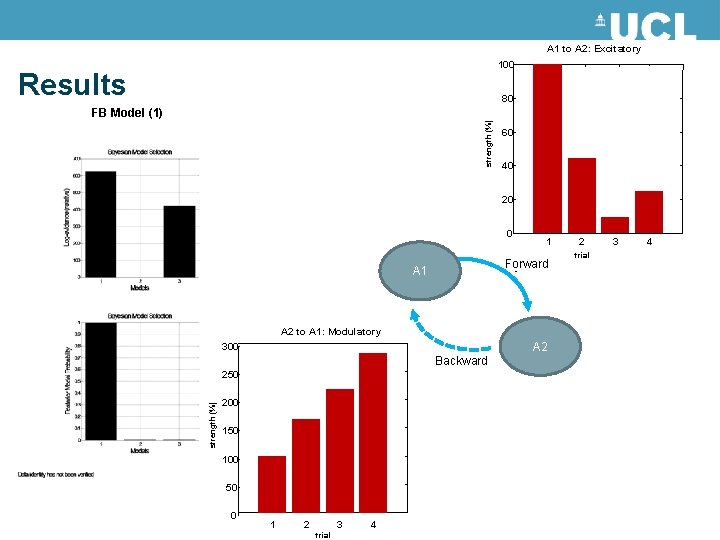
Models FB Model (1) Forward (Excitatory Connection) A 1 A 2 F Model (2) Backward (Inhibitory Connection) Forward (Excitatory Connection) A 1 Forward (Excitatory Connection) A 2 L Model (3) Lateral (Mixed Connection) A 1 A 2 Lateral (Mixed Connection)

A 1 to A 2: Excitatory 100 Results 80 strength (%) FB Model (1) 60 40 20 0 1 Forward A 1 A 2 to A 1: Modulatory A 2 300 Backward strength (%) 250 200 150 100 50 0 1 2 3 trial 4 2 trial 3 4

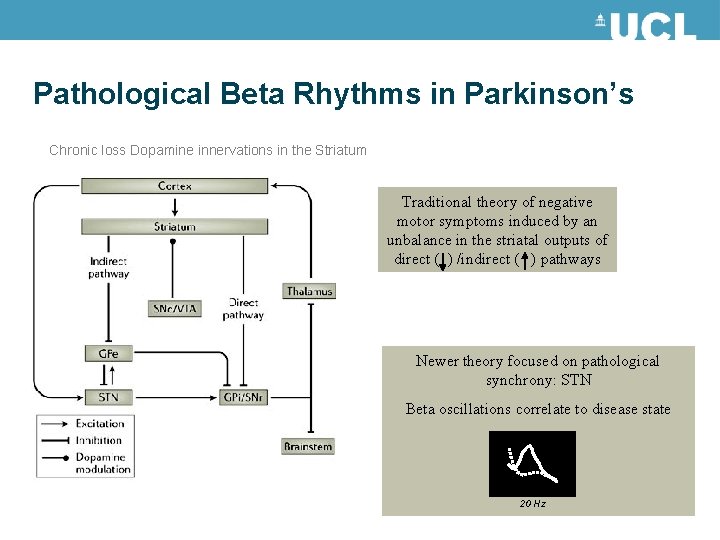
Pathological Beta Rhythms in Parkinson’s Chronic loss Dopamine innervations in the Striatum Traditional theory of negative motor symptoms induced by an unbalance in the striatal outputs of direct ( ) /indirect ( ) pathways Newer theory focused on pathological synchrony: STN Beta oscillations correlate to disease state 20 Hz

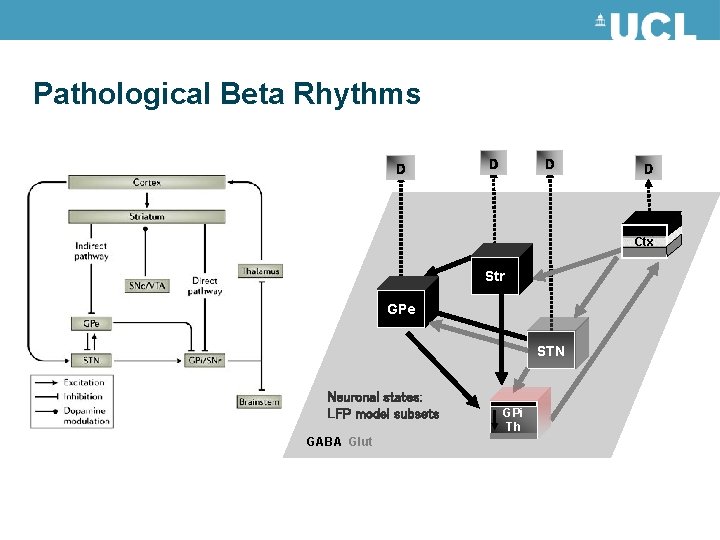
Pathological Beta Rhythms D D Ctx Str GPe STN Neuronal states: LFP model subsets GABA Glut GPi Th

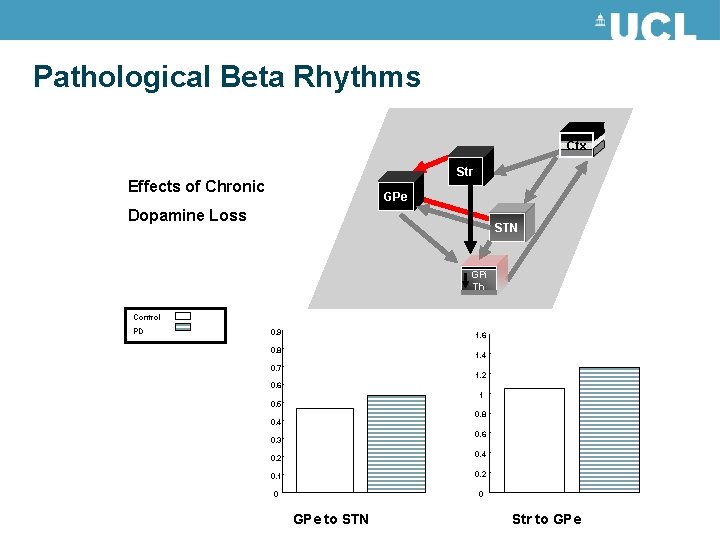
Pathological Beta Rhythms Ctx Str Effects of Chronic GPe Dopamine Loss STN GPi Th Control PD 0. 9 1. 6 0. 8 1. 4 0. 7 1. 2 0. 6 1 0. 5 0. 8 0. 4 0. 6 0. 3 0. 2 0. 4 0. 1 0. 2 0 0 GPe to STN Str to GPe

Summary • DCM is a generic framework for asking mechanistic questions of neuroimaging data • Neural mass models parameterise intrinsic and extrinsic ensemble connections and synaptic measures • DCM for SSR is a compact characterisation of multi- channel LFP or EEG data in the Frequency Domain • Bayesian inversion provides parameter estimates and allows model comparison for competing hypothesised architectures • Empirical results suggest valid physiological predictions