Dyadic designs to model relations in social interaction

Dyadic designs to model relations in social interaction data Todd D. Little Yale University

Outline • Why have such a symposium • Dyadic Designs and Analyses • Thoughts on Future Directions

Some Bad Methods • Dyad-level Setups (Ignore individuals) • Target-Partner Setups • Arbitrary assignment of target vs partner • Loss of power • Often underestimates relations • Ignores dyadic impact • Target with multiple-Partner • Take average of partners to reduce dyadlevel influences • Doesn't really do it • Ignores dyadic impact

Intraclass Setups • Represents target with partner & partner with target in same data structure • Exchangeable case (target/partner arbitrary) • Distinguishable case (something systematic) • Keeps dyadic influence • Contains dependencies • Requires adjustments for accurate statistical inferences (see e. g. , Gonzalez & Griffin)

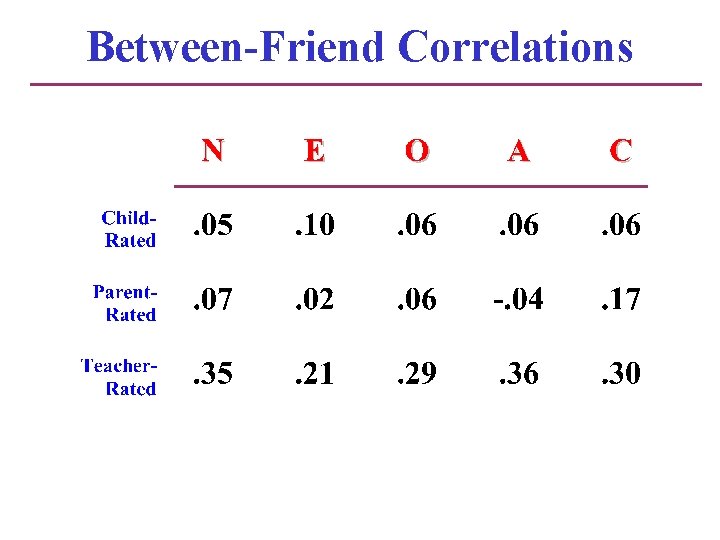
Between-Friend Correlations

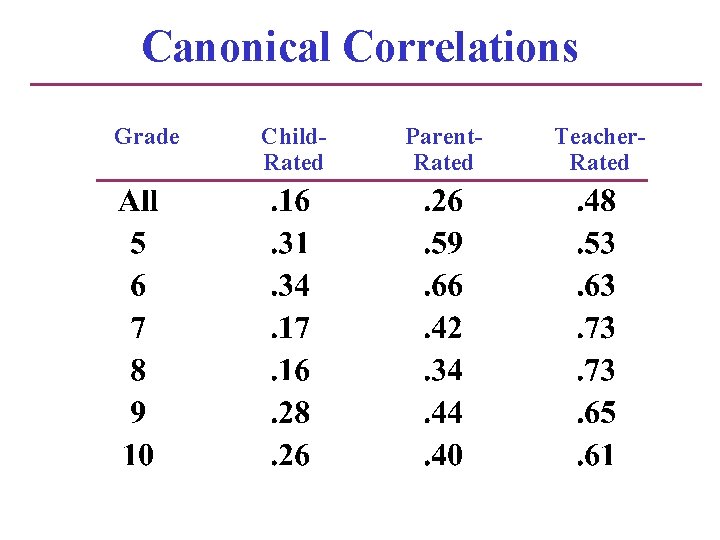
Canonical Correlations Grade Child. Rated Parent. Rated Teacher. Rated

Social Relations Model (Kenny et al. ) • Xijk = mk + ai + bj + gij + eijk Where Xijk is the actor i's behavior with partner j at occasion k mk is a grand mean or intercept ai is variance unique to the actor i bj is variance unique to the partner j gij is variance unique to the ij-dyad eijk is error variance • Round-Robin designs: (n * (n-1) / 2) • Sample from all possible interactions • Block designs: p persons interact with q persons • Checker-board: multiple p's and q's of 2 or more

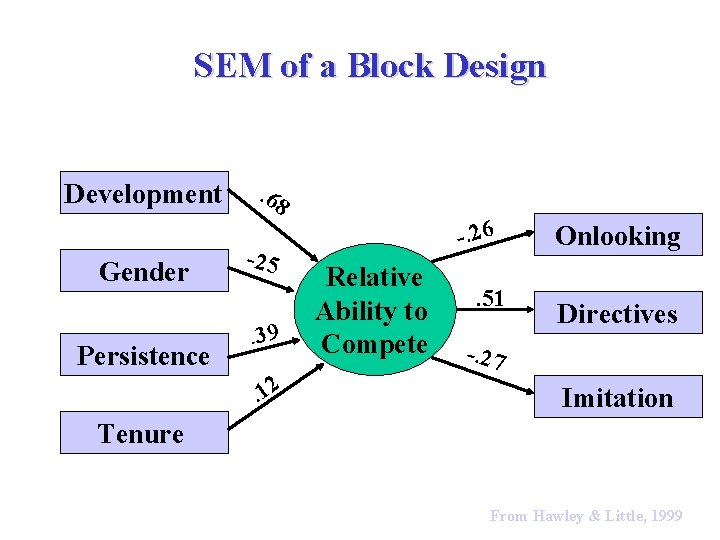
SEM of a Block Design Development Gender Persistence . 68 -25 . 39 . 12 -. 26 Relative Ability to Compete . 51 Onlooking Directives -. 27 Imitation Tenure From Hawley & Little, 1999

Multilevel Approaches • Distinguish HLM (a specific program) from hierarchical linear modeling, the technique – A generic term for a type of analysis • Probably best to discuss MRC(M) Modeling – Multilevel Random Coefficient Modeling • Different program implementations – HLM, MLn, SAS, BMDP, LISREL, and others

"Once you know that hierarchies exist, you see them everywhere. " -Kreft and de Leeuw (1998)

Logic of MRCM • Coefficients describing level 1 phenomena are estimated within each level 2 unit (e. g. , individuallevel effects) – Intercepts—means – Slopes—covariance/regression coefficients • Level 1 coefficients are also analyzed at level 2 (e. g. , dyad-level effects) – Intercepts: mean effect of dyad – Slopes: effects of dyad-level predictors

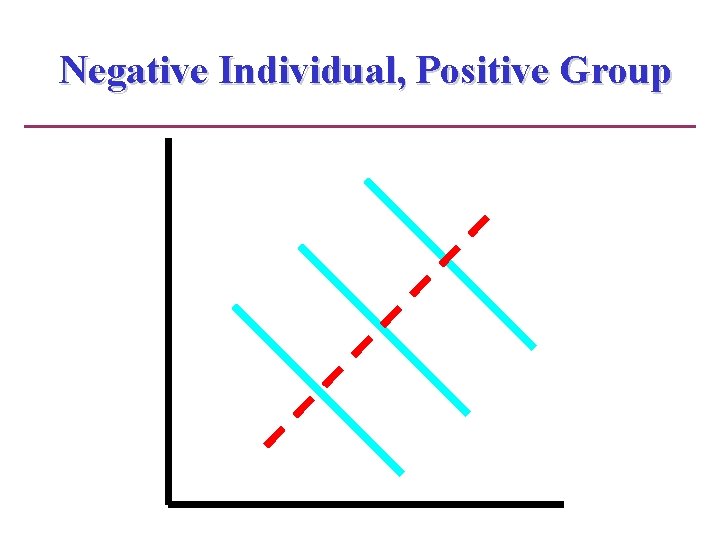
Negative Individual, Positive Group

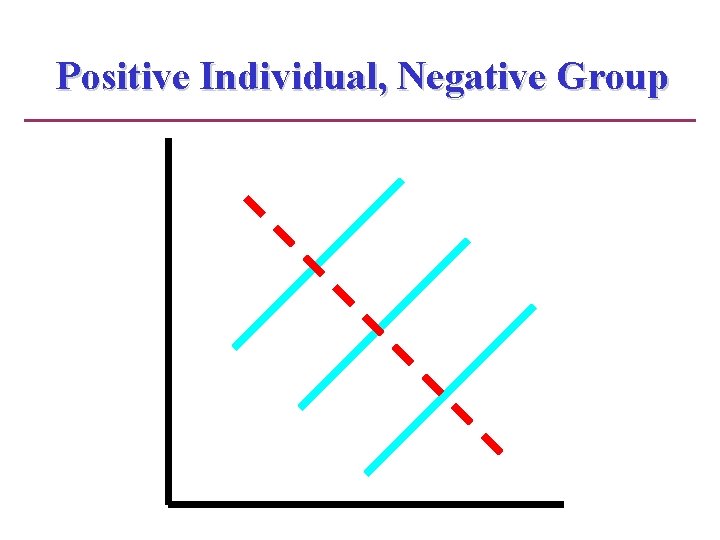
Positive Individual, Negative Group

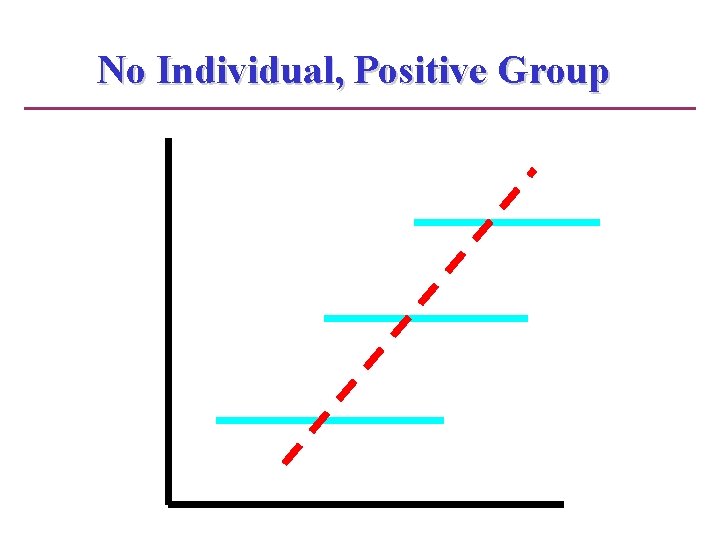
No Individual, Positive Group

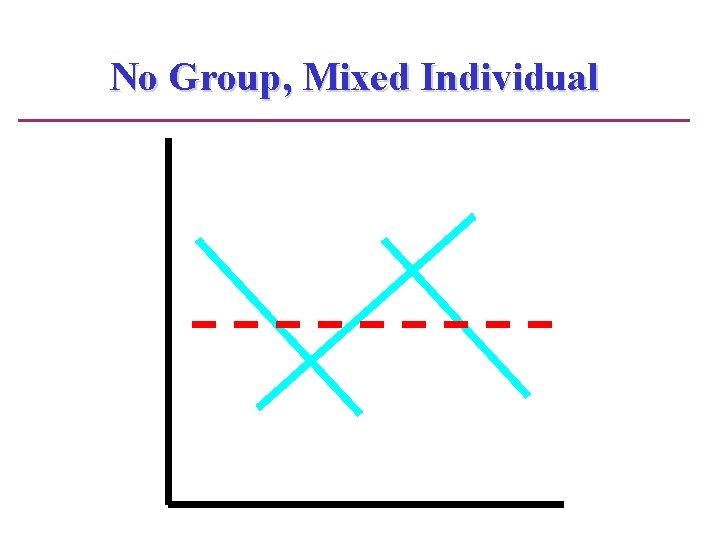
No Group, Mixed Individual

A Contrived Example • Yij = Friendship Closeness ratings of each individual i within each dyad j. • Level 1 Measures: Age & Social Skill of the individual participants • Level 2 Measures: Length of Friendship & Gender Composition of Friendship

The Equations The Level 1 Equation: yij = 0 j + 1 j. Age + 2 j. Soc. Skill + 3 j. Age*Skill + rij The Level 2 Equations: 0 j = 00 + 01(Time) + 02(Gnd) + 03(Time*Gnd) + u 0 j 1 j = 10 + 11(Time) + 12(Gnd) + 13(Time*Gnd) + u 1 j 2 j = 20 + 21(Time) + 22(Gnd) + 23(Time*Gnd) + u 2 j 3 j = 30 + 31(Time) + 32(Gnd) + 33(Time*Gnd) + u 3 j

Future Directions • OLS vs. ML estimator and bias • Individual-oriented data vs. dyad-oriented data • Thoughts on Future Directions

Level 1 Equations: Meaning of Intercepts • Y = Friendship Closeness Ratings – i individuals – across j dyads – rij individual level error • Intercept (Dyad-mean Closeness) – Yij = 0 j + rij

Level 2 Equations: Meaning of Intercepts • Do Dyad Means Differ? • Mean Closeness across Dyads – 0 j = 00 + u 0 j • Mean Closeness and dyad-level variables (time together and gender composition) – 0 j = 00 + 01 (TIME) + 02 (Gen) + u 0 j

Level 1 Equations: Meaning of Slope • E. g. , Relationship between Closeness and Social Skill within each dyad – Yij = 0 j + 2 j (Soc. Skil) + rij • Intercept for each dyad: 0 j • Social Skill slope for each dyad: 2 j

Level 2 Equations: Meaning of Slopes • Mean Social Skill-Closeness relationship across all dyads – 1 j = 10 + u 1 j • Does Soc. Skill-Closeness relationship vary as a function of how long the dyad has been together? – 1 j = 10 + 11(TIME) + u 1 j