Dvourozmrn geometrick tvary Dvojice hl 2 Souhlasn a

Dvourozměrné geometrické útvary Dvojice úhlů - 2 Souhlasné a střídavé úhly. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

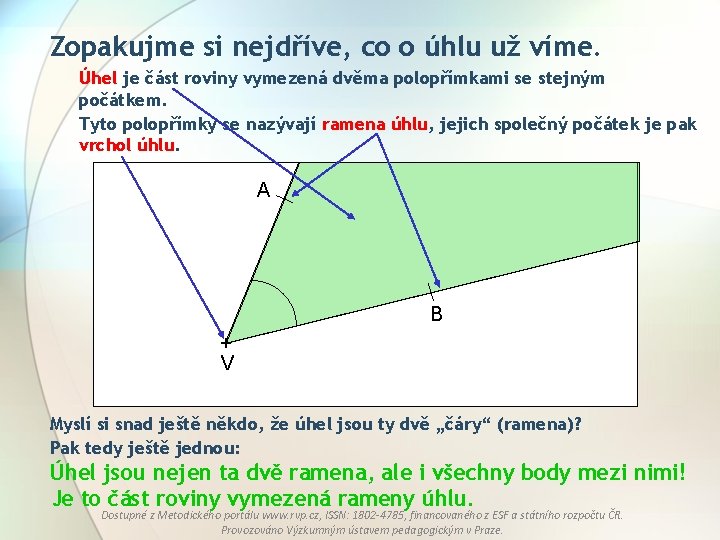
Zopakujme si nejdříve, co o úhlu už víme. Úhel je část roviny vymezená dvěma polopřímkami se stejným počátkem. Tyto polopřímky se nazývají ramena úhlu, jejich společný počátek je pak vrchol úhlu. A B + V Myslí si snad ještě někdo, že úhel jsou ty dvě „čáry“ (ramena)? Pak tedy ještě jednou: Úhel jsou nejen ta dvě ramena, ale i všechny body mezi nimi! Je to část roviny vymezená rameny úhlu. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

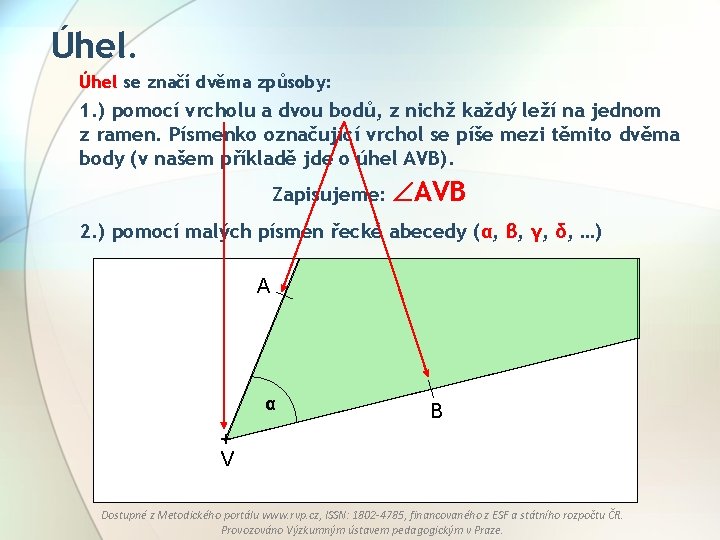
Úhel se značí dvěma způsoby: 1. ) pomocí vrcholu a dvou bodů, z nichž každý leží na jednom z ramen. Písmenko označující vrchol se píše mezi těmito dvěma body (v našem příkladě jde o úhel AVB). Zapisujeme: AVB 2. ) pomocí malých písmen řecké abecedy (α, β, γ, δ, …) A α B + V Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

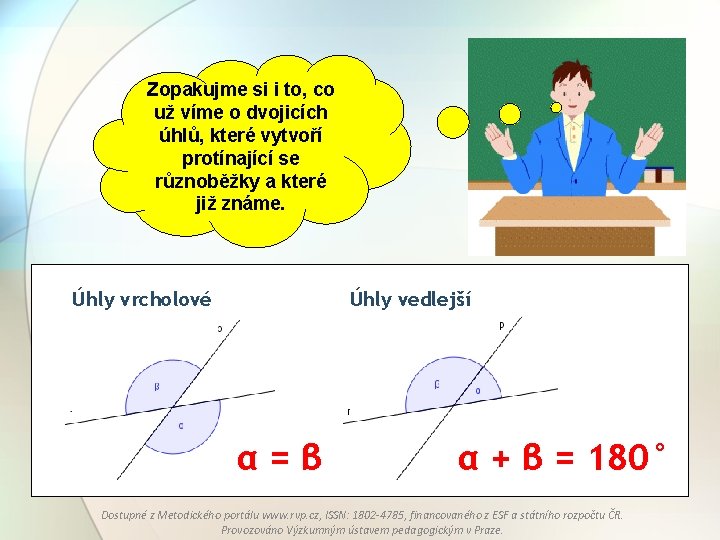
Zopakujme si i to, co už víme o dvojicích úhlů, které vytvoří protínající se různoběžky a které již známe. Úhly vrcholové Úhly vedlejší α=β α + β = 180° Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

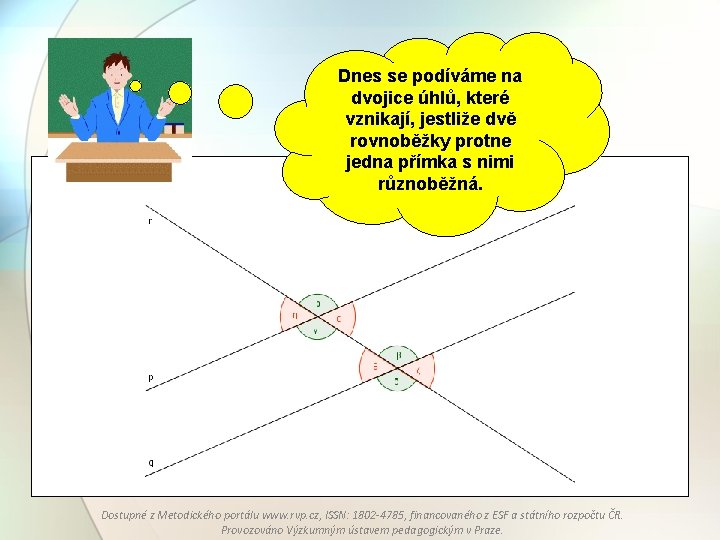
Dnes se podíváme na dvojice úhlů, které vznikají, jestliže dvě rovnoběžky protne jedna přímka s nimi různoběžná. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

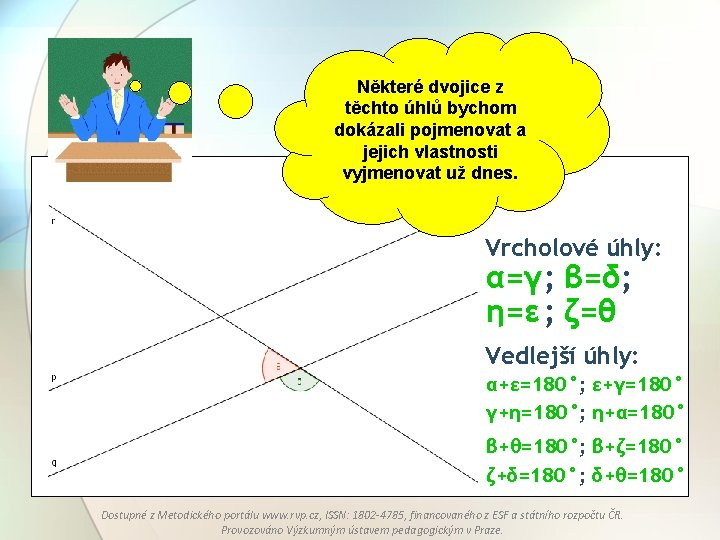
Některé dvojice z těchto úhlů bychom dokázali pojmenovat a jejich vlastnosti vyjmenovat už dnes. Vrcholové úhly: α=γ; β=δ; η=ε; ζ=θ Vedlejší úhly: α+ε=180°; ε+γ=180° γ+η=180°; η+α=180° β+θ=180°; β+ζ=180° ζ+δ=180°; δ+θ=180° Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

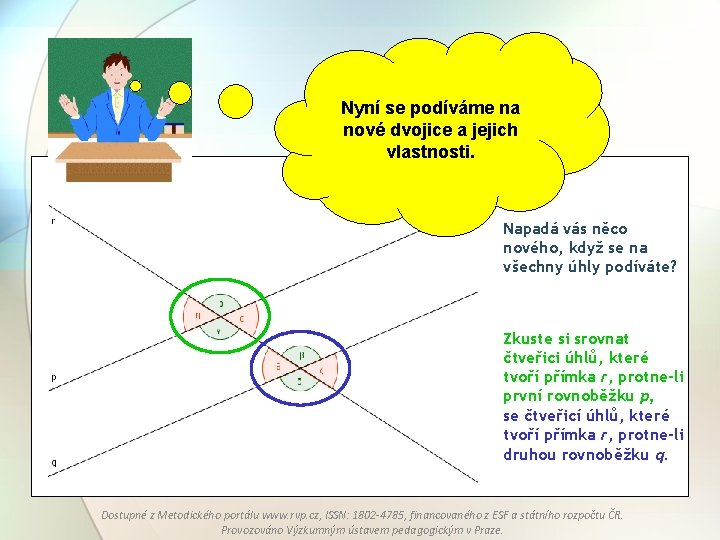
Nyní se podíváme na nové dvojice a jejich vlastnosti. Napadá vás něco nového, když se na všechny úhly podíváte? Zkuste si srovnat čtveřici úhlů, které tvoří přímka r, protne-li první rovnoběžku p, se čtveřicí úhlů, které tvoří přímka r, protne-li druhou rovnoběžku q. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

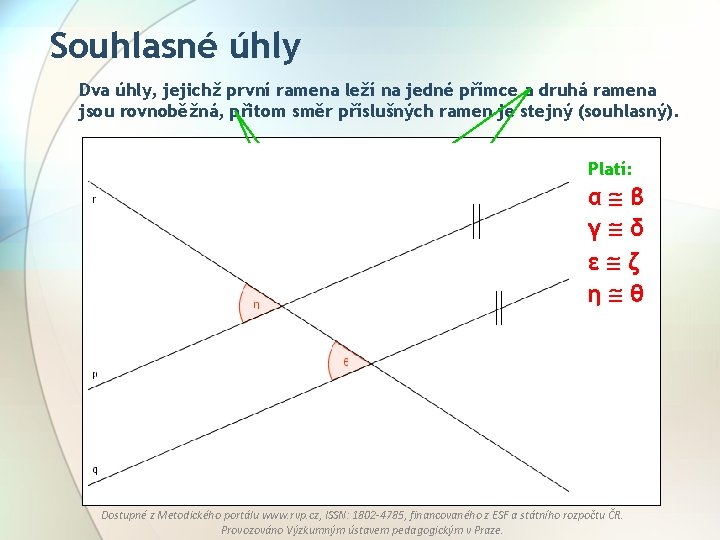
Souhlasné úhly Dva úhly, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je stejný (souhlasný). Platí: α β γ δ ε ζ η θ Souhlasné úhly jsou shodné. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

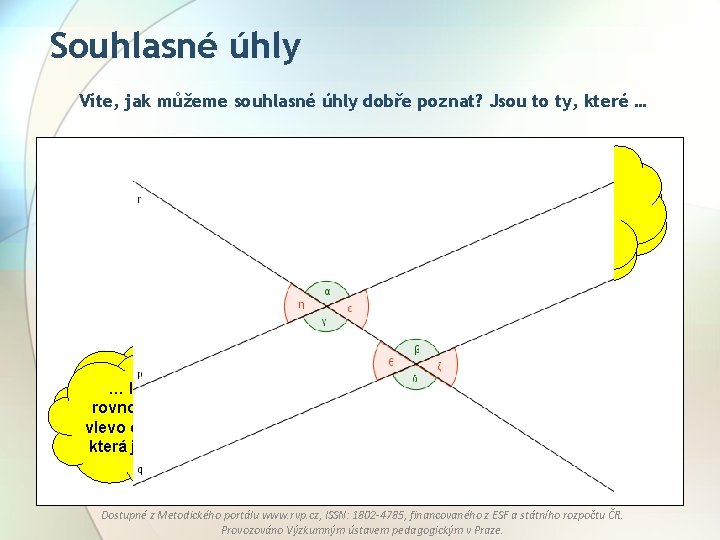
Souhlasné úhly Víte, jak můžeme souhlasné úhly dobře poznat? Jsou to ty, které … … leží pod … leží nad rovnoběžkami, vpravo od je přímky, která je protíná. … leží pod … leží nad rovnoběžkami, vlevo od přímky, vlevo od která je přímky, protíná. která je protíná. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

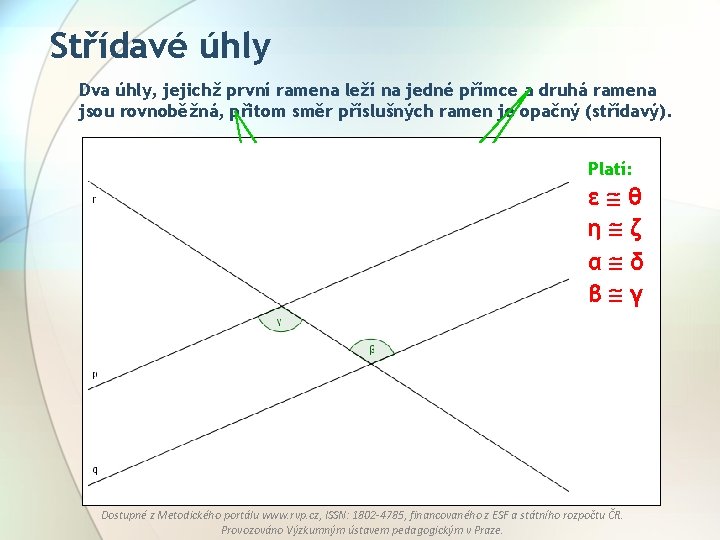
Střídavé úhly Dva úhly, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je opačný (střídavý). Platí: ε θ η ζ α δ β γ Střídavé úhly jsou shodné. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

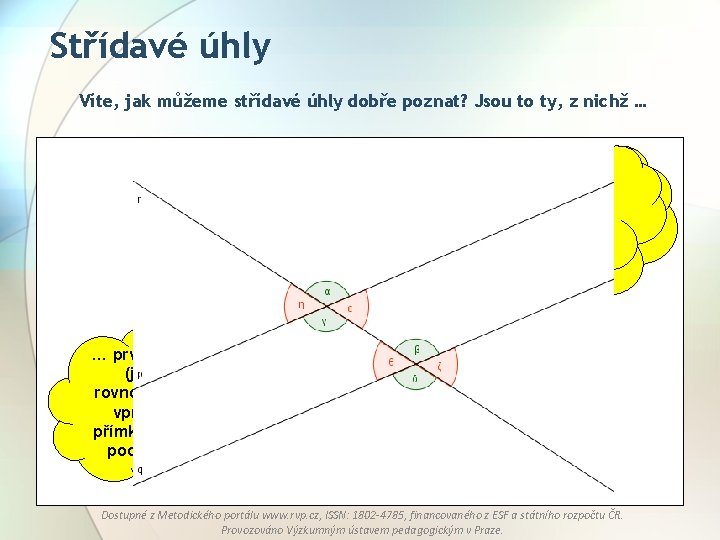
Střídavé úhly Víte, jak můžeme střídavé úhly dobře poznat? Jsou to ty, z nichž … … první leží pod (první rovnoběžkou) a vpravo … první leží nad (od ji a přímky, vpravo, která druhý protíná) leží podaadruhý vlevo. nad (druhou rovnoběžkou) a vlevo (od přímky). … první leží nad (jednou … první leží nad rovnoběžkou) a a vlevo a druhý vpravo (od pod a vpravo. přímky) a druhý pod a vlevo. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

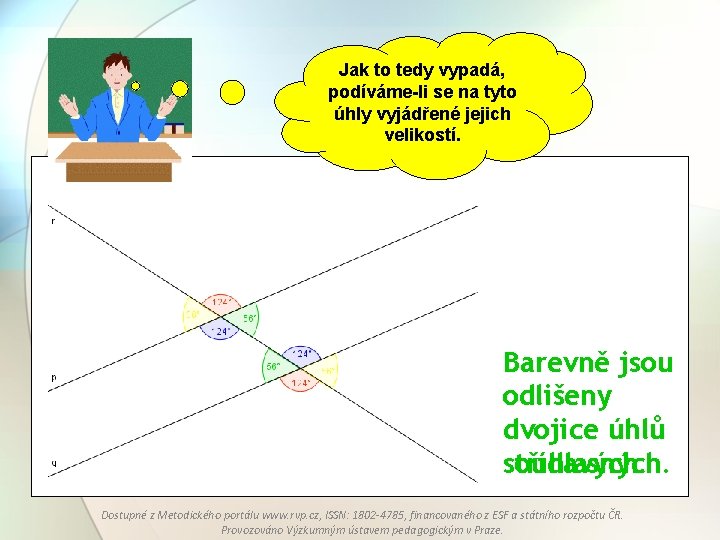
Jak to tedy vypadá, podíváme-li se na tyto úhly vyjádřené jejich velikostí. Barevně jsou odlišeny dvojice úhlů souhlasných. střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

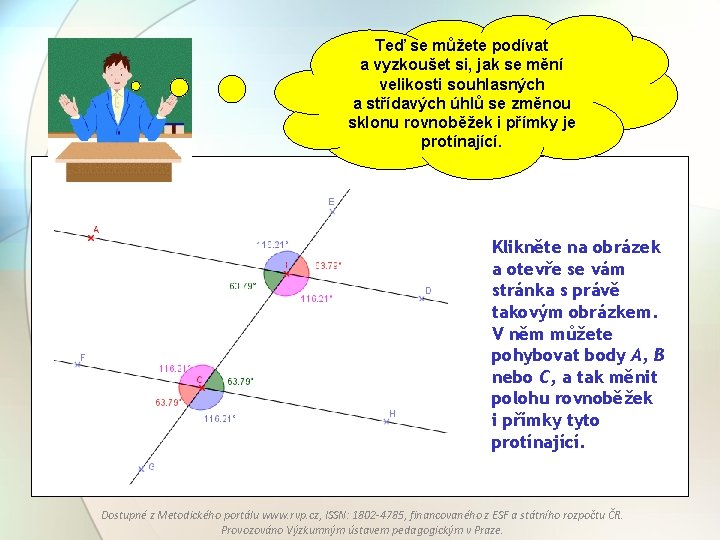
Teď se můžete podívat a vyzkoušet si, jak se mění velikosti souhlasných a střídavých úhlů se změnou sklonu rovnoběžek i přímky je protínající. Klikněte na obrázek a otevře se vám stránka s právě takovým obrázkem. V něm můžete pohybovat body A, B nebo C, a tak měnit polohu rovnoběžek i přímky tyto protínající. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

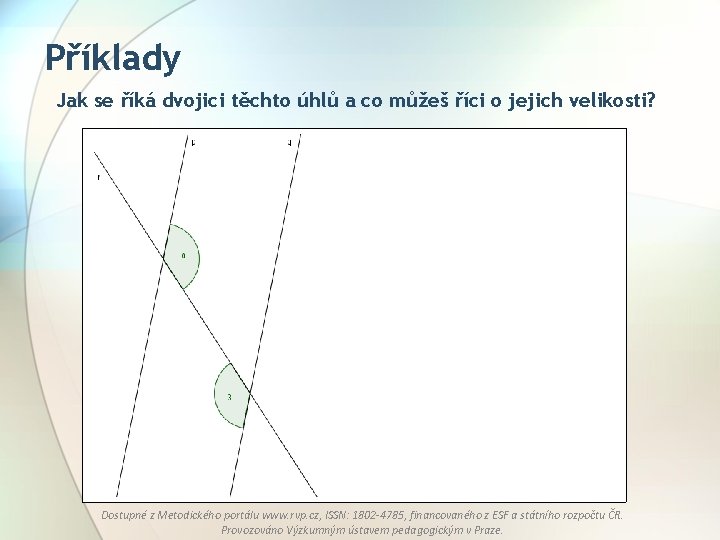
Příklady Jak se říká dvojici těchto úhlů a co můžeš říci o jejich velikosti? Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

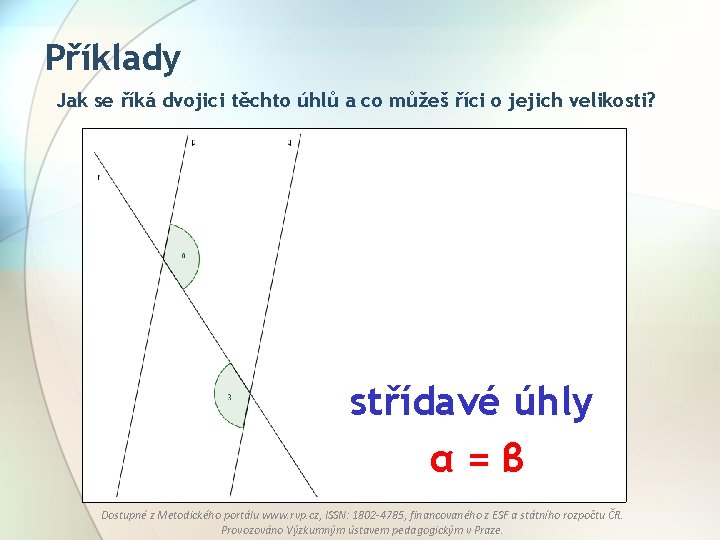
Příklady Jak se říká dvojici těchto úhlů a co můžeš říci o jejich velikosti? střídavé úhly α=β Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

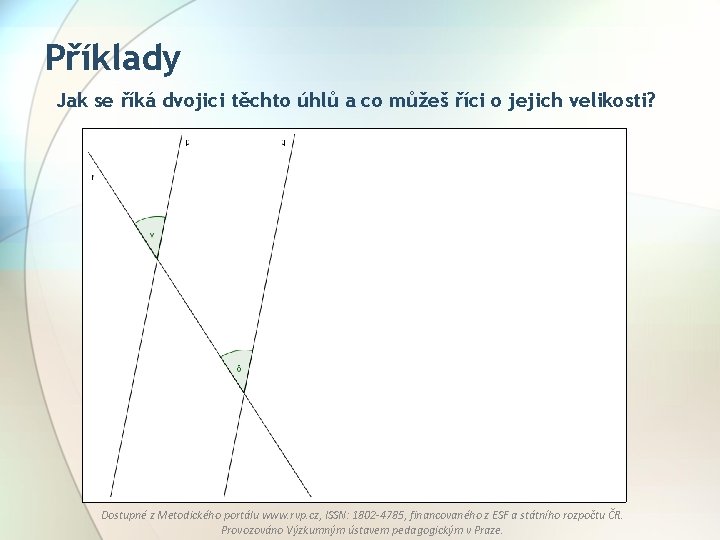
Příklady Jak se říká dvojici těchto úhlů a co můžeš říci o jejich velikosti? Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Příklady Jak se říká dvojici těchto úhlů a co můžeš říci o jejich velikosti? souhlasné úhly γ=δ Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

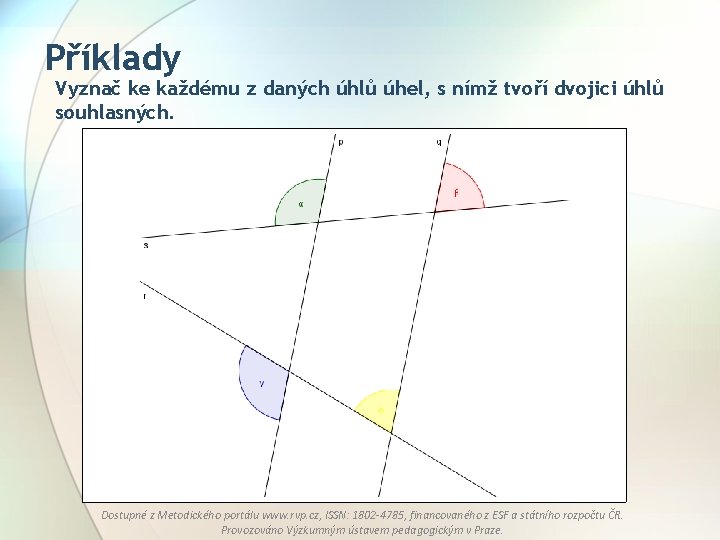
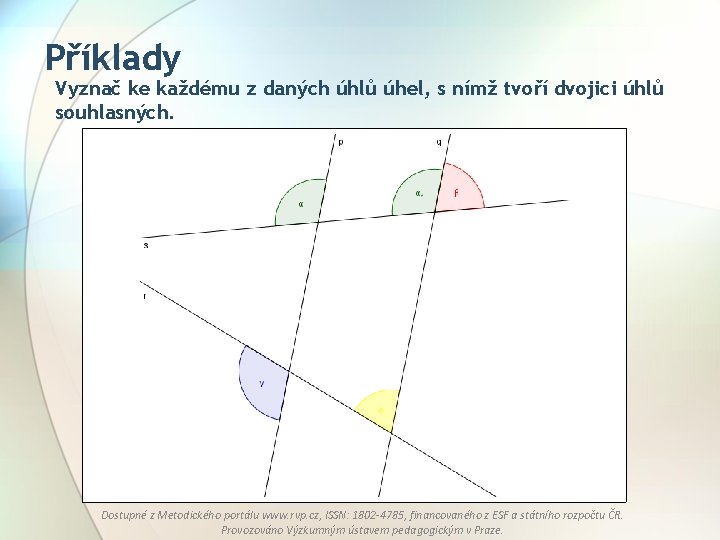
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů souhlasných. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

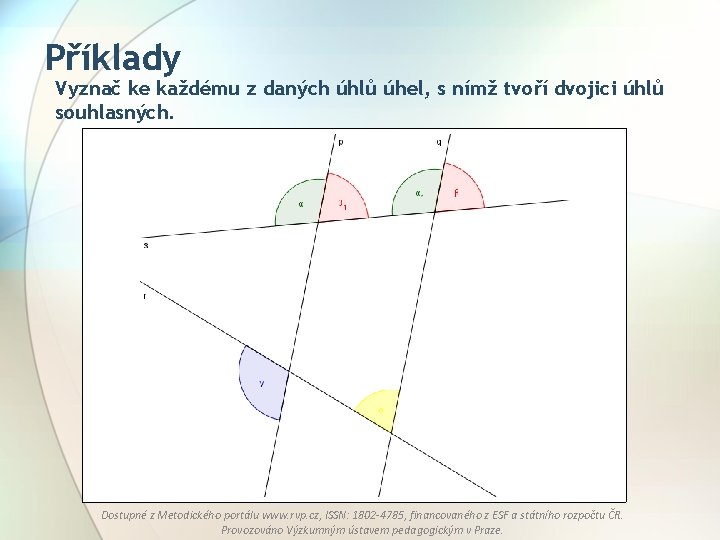
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů souhlasných. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

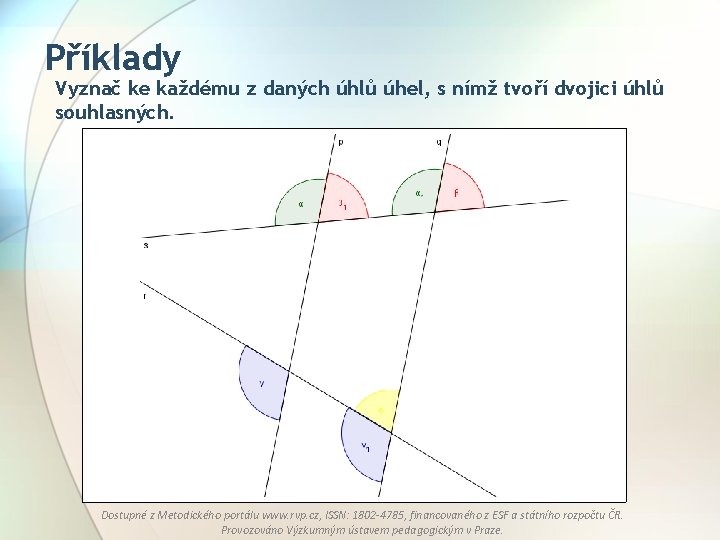
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů souhlasných. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

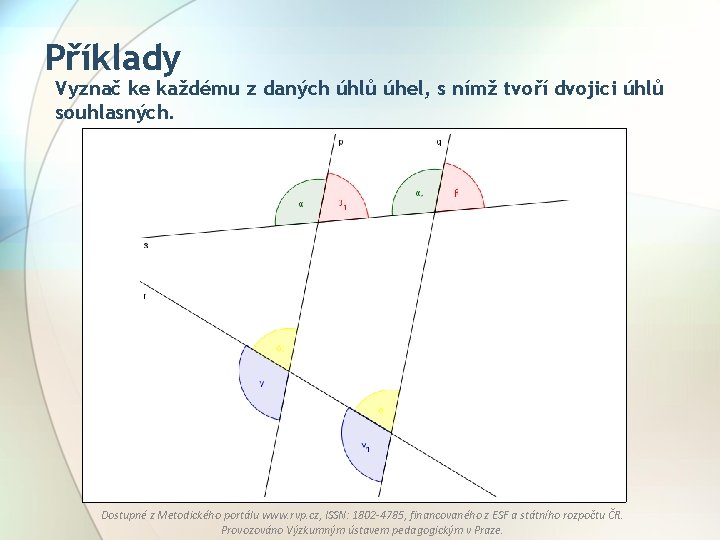
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů souhlasných. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů souhlasných. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

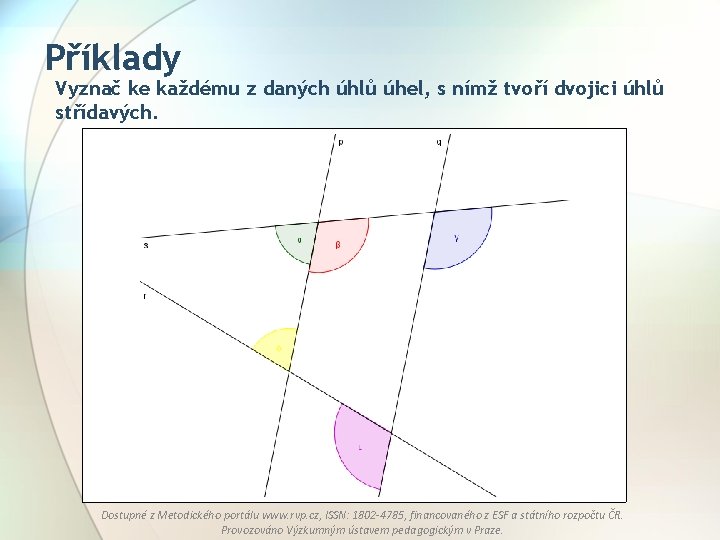
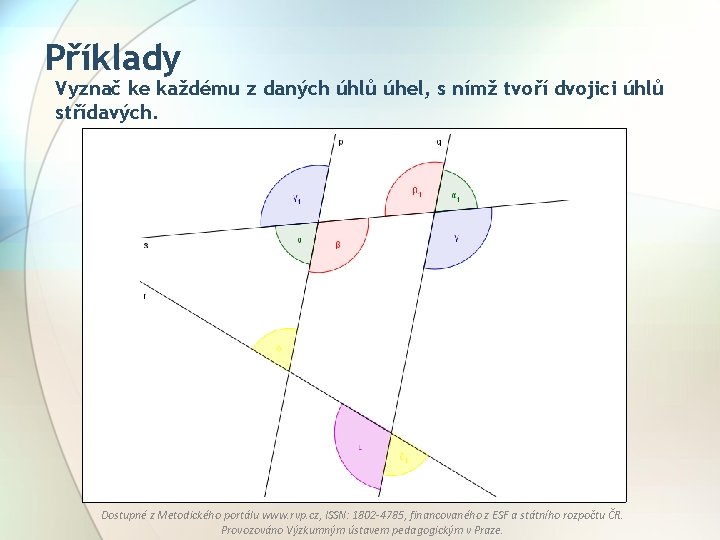
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

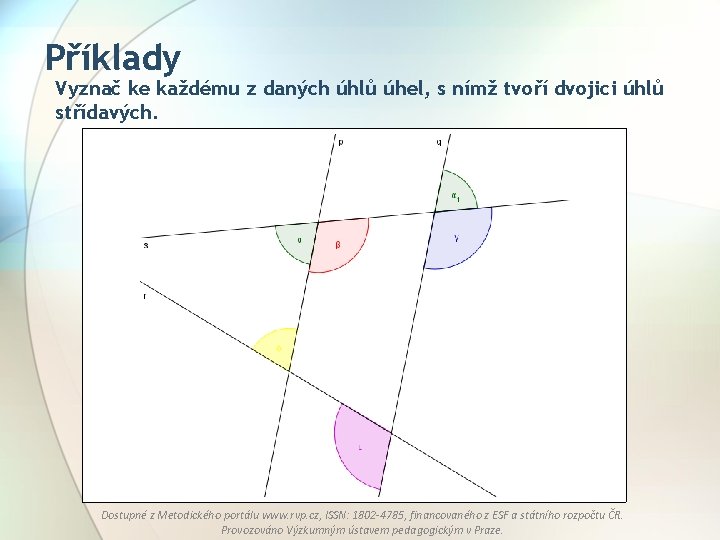
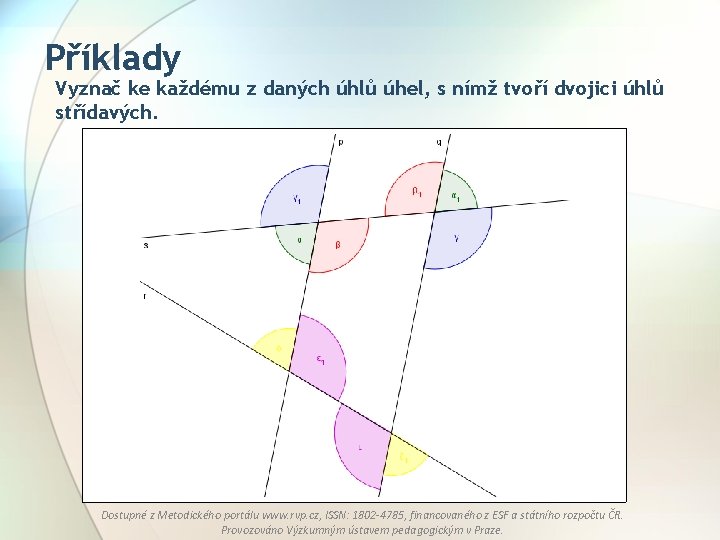
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

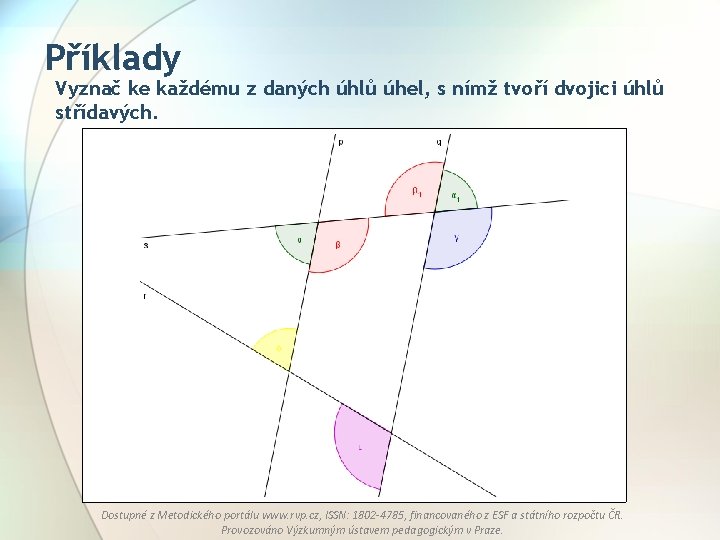
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

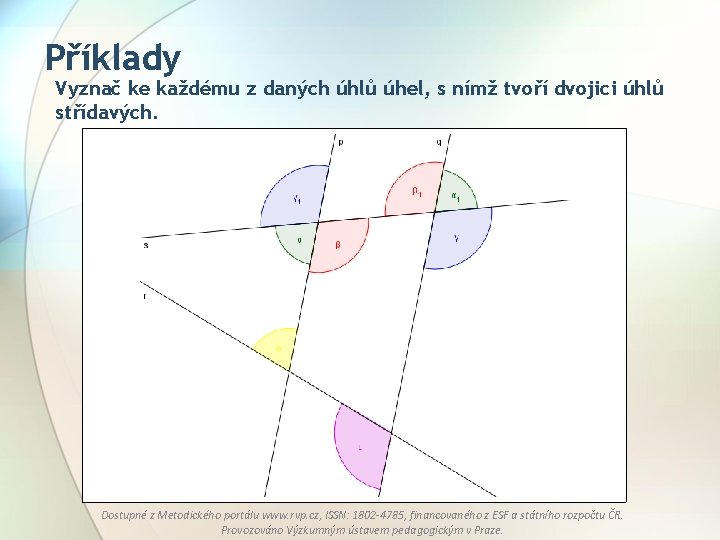
Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Příklady Vyznač ke každému z daných úhlů úhel, s nímž tvoří dvojici úhlů střídavých. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

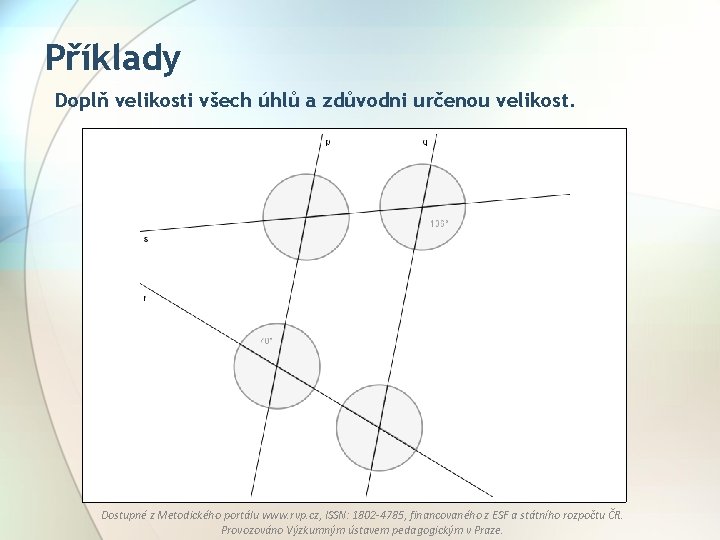
Příklady Doplň velikosti všech úhlů a zdůvodni určenou velikost. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

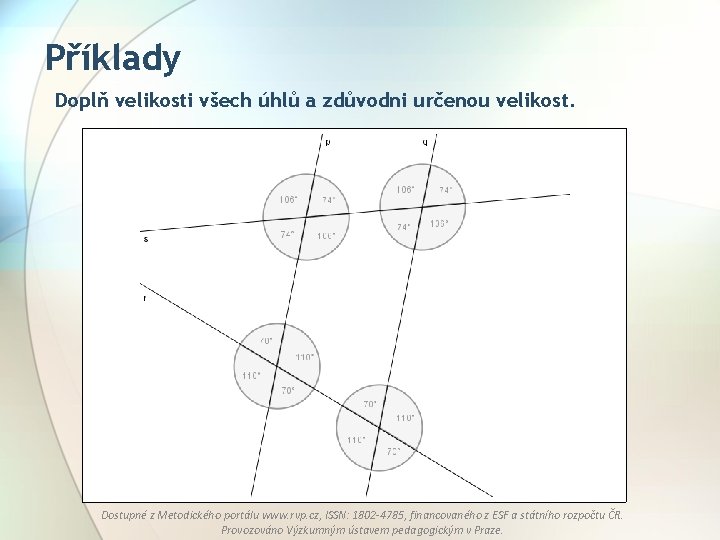
Příklady Doplň velikosti všech úhlů a zdůvodni určenou velikost. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

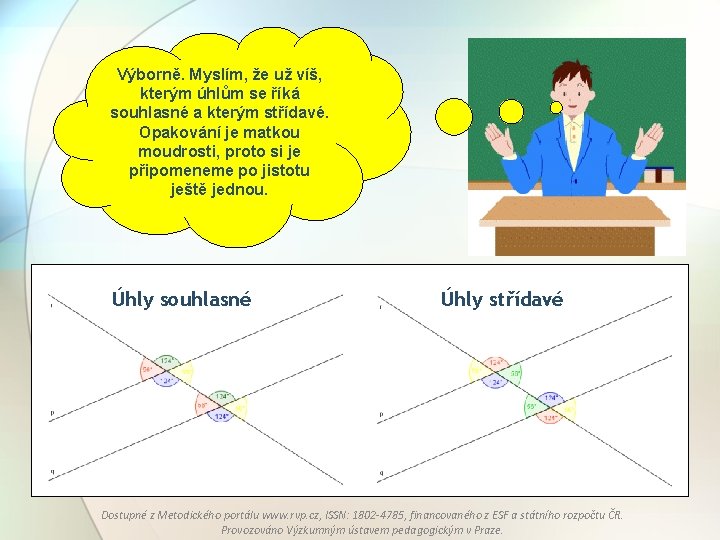
Výborně. Myslím, že už víš, kterým úhlům se říká souhlasné a kterým střídavé. Opakování je matkou moudrosti, proto si je připomeneme po jistotu ještě jednou. Úhly souhlasné Úhly střídavé Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.