Dvodimenzionalni nizovi matrice Do sada smo imali prilike

Dvodimenzionalni nizovi - matrice

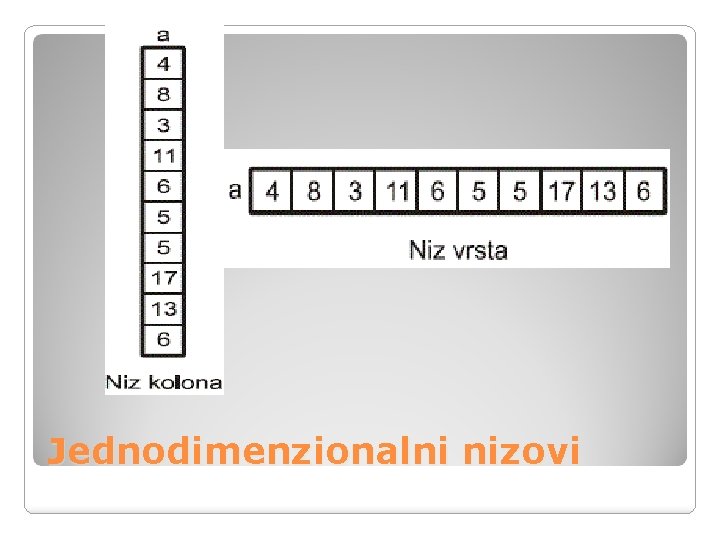
Do sada smo imali prilike da se upoznamo sa JEDNODIMENZIONALNIM nizovima čiji su elementi skalarne veličine – celi i realni brojevi, znakovi. . . Svakom elementu niza smo pristupali pomoću jedne indeksne promenljive(i, j ili k) Ovakvi nizovi se šematski mogu prikazati kao horizontalna ili vertikalna lista podataka

Jednodimenzionalni nizovi

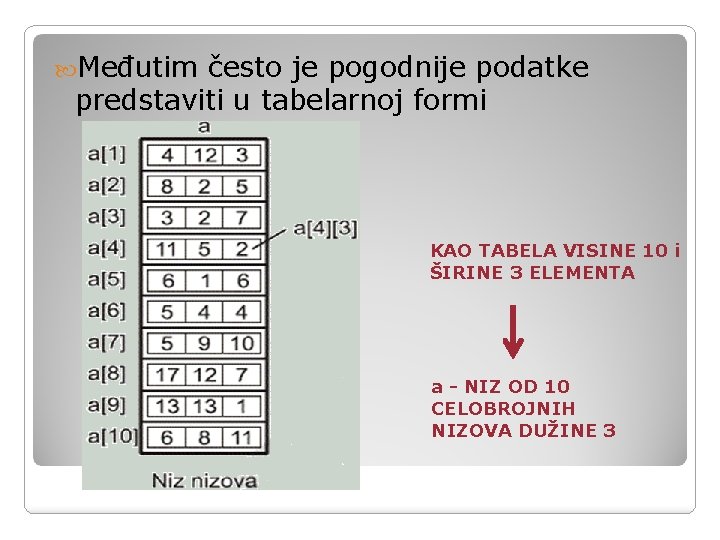
Međutim često je pogodnije podatke predstaviti u tabelarnoj formi KAO TABELA VISINE 10 i ŠIRINE 3 ELEMENTA a - NIZ OD 10 CELOBROJNIH NIZOVA DUŽINE 3

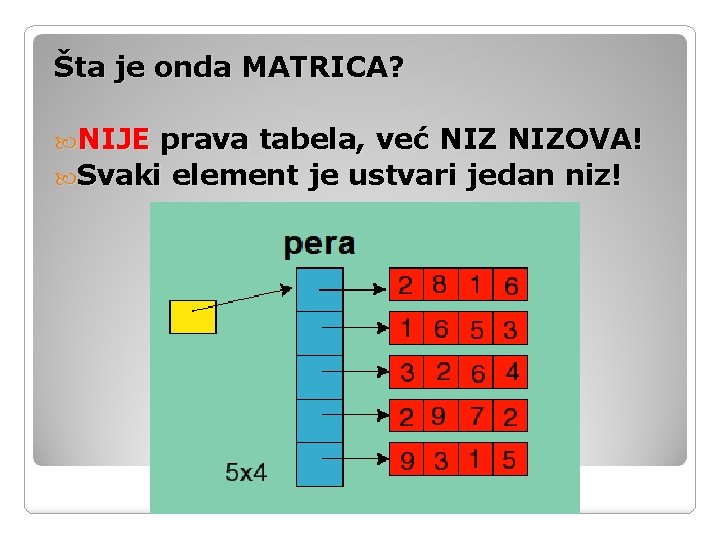
Šta je onda MATRICA? NIJE prava tabela, već NIZOVA! Svaki element je ustvari jedan niz!

pera je matrica čiji su elementi NIZOVI od po 4 broja – tipa integer! pera[1] je prvi element koji je NIZ! Svaki element ima SVOJE ELEMENTE! pera[1][1] pera[1][2] pera[1][3] pera[1][4] = = 2 8 1 6 Prvo odaberemo podniz pa onda element u njemu!

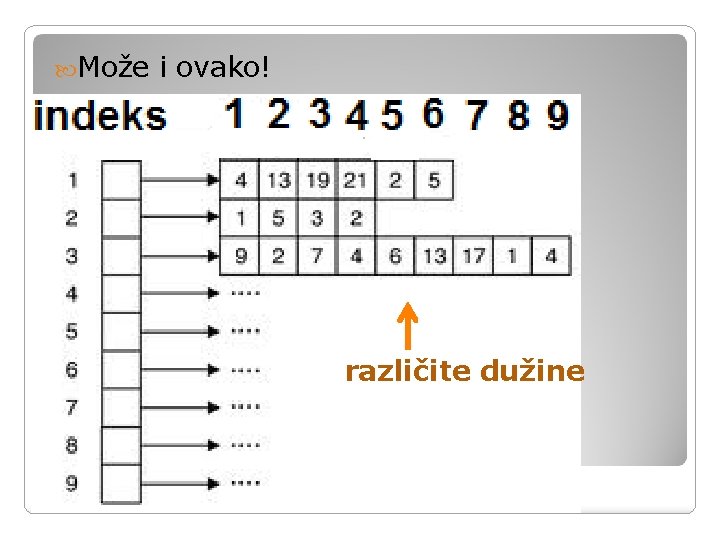
Može i ovako! različite dužine

Pri zadavanju matrice koriste se prirodni brojevi n i m koji definišu dimenziju(n*m) matrice – ukazuju da se matrica sastoji od n vrsta i m kolona. Svaki element aij matrice se karakteriše sa dva indeksa: ◦ PRVI određuje VRSTU ◦ DRUGI određuje KOLONU Npr. matrica a od najviše 10 vrsta i 3 kolone se definiše na sledeći način: var a: array[1. . 10, 1. . 3] of real; ovoliko mesta se izdvoji u memoriji

Ovde se zadaju dva indeksa! Elementu u i-toj vrsti i j-toj koloni se može pristupiti korišćenjem zapisa a[i][j] ili a[i, j] i – redni broj vrste j – redni broj kolone Npr. elementu druge vrste i treće kolone moguće je pristupiti kao a[2, 3] Pojedinačnoj vrsti se može pristupiti korišćenjem zapisa a[i], gde je i redni broj vrste.

Elementi jedne vrste se mogu kopirati u elemente druge vrste … Npr. a[5] = a[1] – elementi prve vrste se kopiraju u odgovarajuće elemente pete vrste

Unos elemenata u matricu writeln(‘Učitaj vrednosti elemenata matrice: ’); for i: =1 to n do for j: =1 to m do read(a[i, j]); Ispis elemenata matrice for i: =1 to n do begin for j: =1 to m do write(a[i, j]); ispisujemo red po red writeln prelazimo u novi red end;

ZADACI: 1. Učitati realnu matricu dimenzija n*m. Ispisati novu matricu koja se sastoji od recipročnih vrednosti elemenata unete matrice. 2. Napisati program koji za odeljenje od najviše 25 učenika i najviše 15 predmeta izračunava: a) prosečne ocene učenika b) prosečne ocene po predmetima na osnovu tabele ocena iz dnevnika. 3. Kovanice od 1, 2, 5, 10 i 20 dinara formiraju kvadratnu matricu para dimenzija n*n. Pronaći: zbir kovanica na glavnoj dijagonali, najmanji element iznad glavne dijagonale.

4. Od unetih elemenata realne matrice n*m formirati i ispisati niz čiji su elementi zbirovi vrsta (redova) matrice. 5. Za unetu dimenziju n kvadratne matrice i uneti broj k ispisati sledeću matricu: 6. Učitati realnu matricu dimenzija n*m. Razmeniti vrednosti elemenata vrste koja sadrži max element sa vrstom u kojoj se nalazi min element.

7. Za unetu kvadratnu matricu a[n*n] pronaći: Zbir elemenata sporedne dijagonale Najveći element iznad sporedne dijagonale Napomena: Za sve zadatke nacrtati algoritamsku šemu i napisati program.