Duality Theory Duality plays an important role in








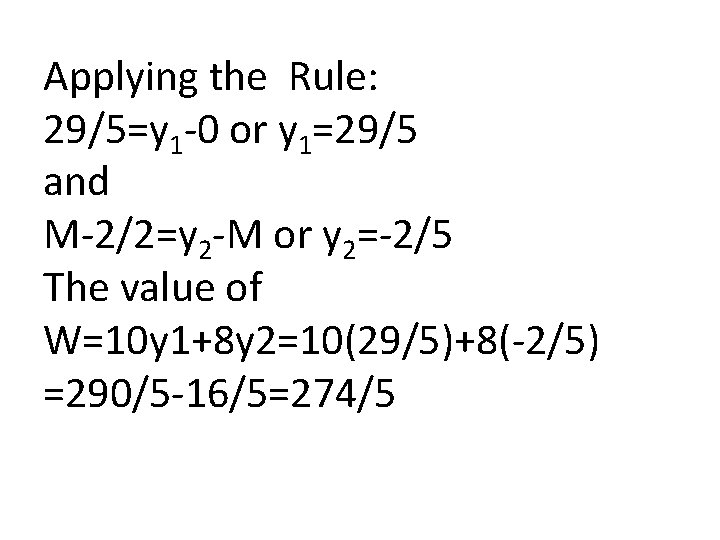
- Slides: 11

Duality Theory: Duality plays an important role in linear as well as non linear programming. When we solve a linear programming problem, unknowingly, we are solving two linear programs, called as Primal and Dual problems. Interestingly, there exist very good relationship between the two programs. In fact, from the solution of one, we can find the solution another problem and vice versa. We investigate this relationship below:

We consider the following Primal and dual problems: Primal: Max Z=5 x 1+12 x 2+4 x 3 Sub to x 1+2 x 2+x 3≤ 10 2 x 1 -x 2+3 x 3=8 x 1, x 2, x 3 ≥ 0 Writing the above LPP as Max Z=5 x 1+12 x 2+4 x 3 Sub to x 1+2 x 2+x 3 ≤ 10 2 x 1 -x 2+3 x 3 ≥ 8, 2 x 1 -x 2+3 x 3 ≤ 8, x 1, x 2, x 3 ≥ 0

We consider the following Primal and dual problems: Primal: Max Z=5 x 1+12 x 2+4 x 3 Sub to x 1+2 x 2+x 3≤ 10 2 x 1 -x 2+3 x 3=8 x 1, x 2, x 3 ≥ 0 Writing the above LPP as Max Z=5 x 1+12 x 2+4 x 3 Sub to x 1+2 x 2+x 3 ≤ 10 2 x 1 -x 2+3 x 3 ≥ 8, 2 x 1 -x 2+3 x 3 ≤ 8, x 1, x 2, x 3 ≥ 0 (We can write the second equality constraint of the primal in the form of two inequalities i. e. , second and third constraint of the Dual)

Now we write the LPP in the symmetric form Max Z=5 x 1+12 x 2+4 x 3 Sub to x 1+2 x 2+x 3≤ 10 2 x 1 -x 2+3 x 3 ≥ 8 -2 x 1+x 2 -3 x 3 ≥ -8 x 1, x 2, x 3 ≥ 0 We write the dual of the above problem as

Min W=10 y 1+8 y 2 -8 y 3 Sub to y 1+2 y 2 -2 y 3 ≥ 5 2 y 1 -y 2 +y 3≥ 12 y 1+3 y 2 -3 y 3 ≥ 4 y 1, y 2, y 3 ≥ 0 we can replace y 2’=y 2 -y 3 and our LPP becomes

Min W=10 y 1+8 y 2’ Sub to y 1+2 y 2’ ≥ 5 2 y 1 -y 2’≥ 12 y 1+3 y 2’≥ 4 y 1≥ 0 and y 2’ becomes unrestricted variable. Therefore, for every equation in Primal problem, there will be a corresponding variable which is unrestricted in sign.

Now, we standardize the Primal, bring it into the canonical form and solve it by using a Big M Method. Max Z=5 x 1+12 x 2+4 x 3+0·x 4+Ma 1 Sub to x 1+2 x 2+x 3+x 4=10 2 x 1 -x 2+3 x 3+a 1=8 x 1, x 2, x 3, x 4≥ 0 and a 1 is an artificial variable.

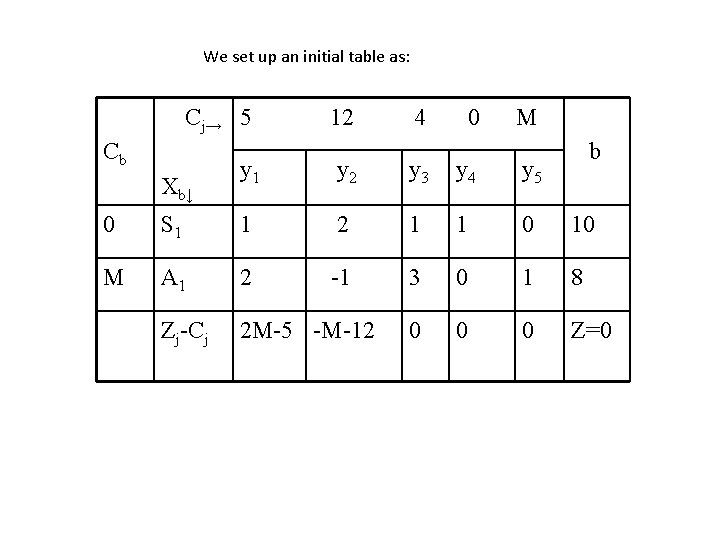
We set up an initial table as: Cj→ 5 Cb Xb↓ 12 4 0 M y 1 y 2 y 3 y 4 y 5 b 0 S 1 1 2 1 1 0 10 M A 1 2 -1 3 0 1 8 Zj-Cj 2 M-5 -M-12 0 0 0 Z=0

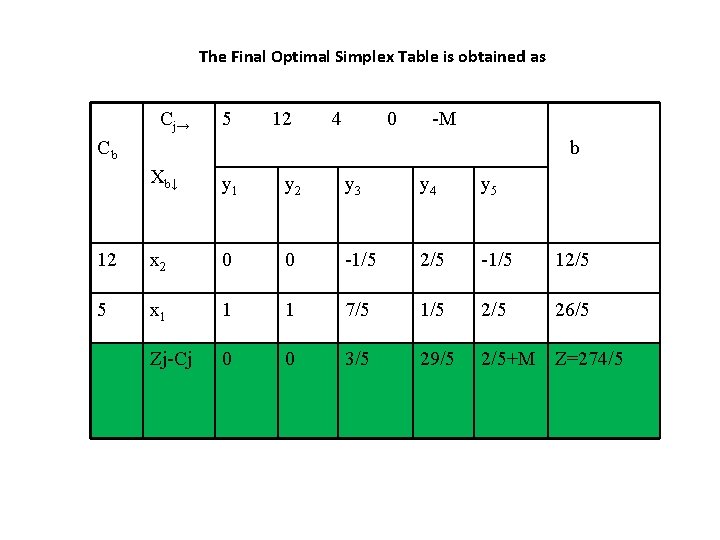
The Final Optimal Simplex Table is obtained as Cj→ 5 12 4 0 -M Cb b Xb↓ y 1 y 2 y 3 y 4 y 5 12 x 2 0 0 -1/5 2/5 -1/5 12/5 5 x 1 1 1 7/5 1/5 26/5 Zj-Cj 0 0 3/5 29/5 2/5+M Z=274/5

In the above table we use the Rule: The Optimal Z-equation coefficients of a starting variables in the Primal = Difference between the left and right sides of the dual constraint associated with the starting variables i. e. , Starting Variables are x 4 a 1 Optimal Z-equation coefficients are 29/5 M-2/5 The dual constraints associated with x 4 and a 1 are y 1 ≥ 0 and y 2 ≥ - M
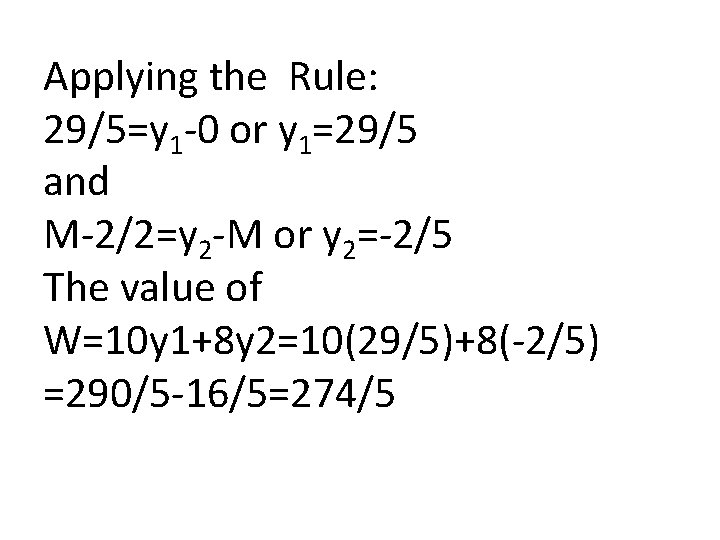
Applying the Rule: 29/5=y 1 -0 or y 1=29/5 and M-2/2=y 2 -M or y 2=-2/5 The value of W=10 y 1+8 y 2=10(29/5)+8(-2/5) =290/5 -16/5=274/5