Dual Sphere Detectors by Krishna Venkateswara Contents Introduction

Dual Sphere Detectors by Krishna Venkateswara

Contents ¡ ¡ ¡ ¡ Introduction Review of noise sources in bar detectors Spherical detectors Dual sphere configuration Sensitivity in SQL Advantages/Drawbacks Dual cylinders and sensitivity Summary

Introduction • Proposed by M. Cerdonio, L. Conti et. al. in 2001 • Two nested spheres • Fabry-Perot cavity as motion sensor Main advantages • Wide bandwidth • Spherical detector

Bar detectors with resonant transducers Noise energy=Thermal + Amplifier + Back-action β = energy coupling factor τ = integration time A large β is needed to reduce thermal noise.

Spherical Detectors ¡ ¡ A sphere has a spherical symmetry and 5 degenerate quadrupole modes. Uniform cross-section to GWs. Can determine both source direction ( , ) and wave polarization (h+, h ). Mount 6 radial transducers on truncated icosahedral configuration. “Spherically symmetric” detection of the sphere (Johnson & Merkowitz, 1993)

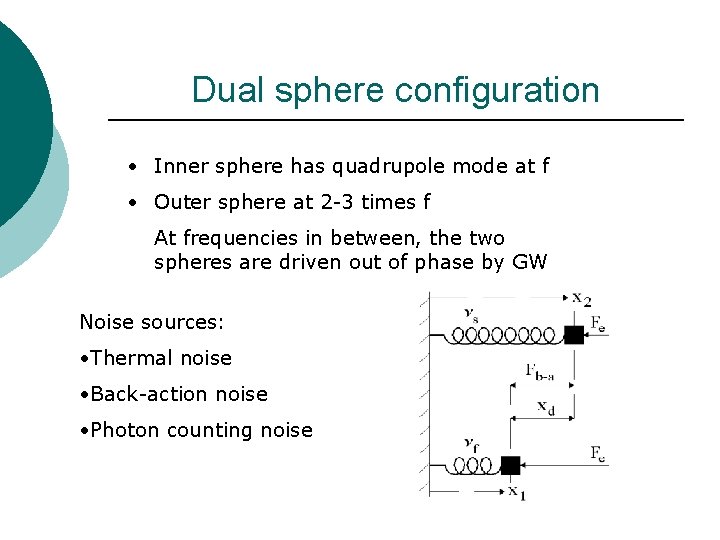
Dual sphere configuration • Inner sphere has quadrupole mode at f • Outer sphere at 2 -3 times f At frequencies in between, the two spheres are driven out of phase by GW Noise sources: • Thermal noise • Back-action noise • Photon counting noise

Response of the surface of a sphere to GW Noise spectral density for each sensor

Total strain noise density

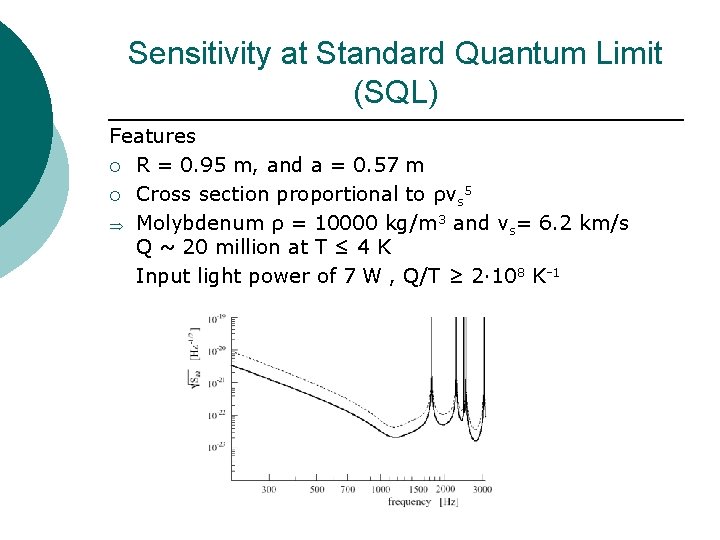
Sensitivity at Standard Quantum Limit (SQL) Features ¡ R = 0. 95 m, and a = 0. 57 m ¡ Cross section proportional to ρvs 5 Molybdenum ρ = 10000 kg/m 3 and vs= 6. 2 km/s Q ~ 20 million at T ≤ 4 K Input light power of 7 W , Q/T ≥ 2· 108 K-1

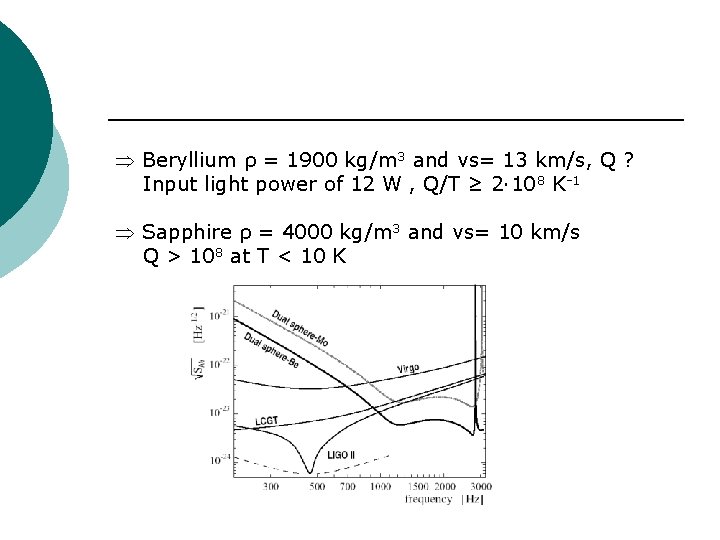
Beryllium ρ = 1900 kg/m 3 and vs= 13 km/s, Q ? Input light power of 12 W , Q/T ≥ 2· 108 K-1 Sapphire ρ = 4000 kg/m 3 and vs= 10 km/s Q > 108 at T < 10 K

Advantages/Drawbacks ¡ ¡ Wideband Spherical detector High sensitivity (at SQL) Different frequency band ¡ ¡ Complicated design Sensor sensitivity difficult to realize

Dual Cylinders ¡ ¡ ¡ Simpler design Each mode contributes to noise while signal is mainly from Quadrupole mode selective readout Low thermal noise from high frequency modes Xd = x 1 – x 2 + x 3 – x 4

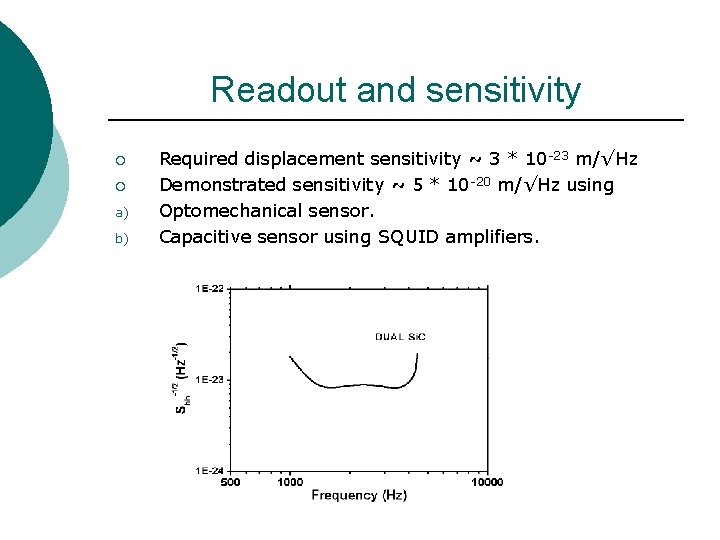
Readout and sensitivity ¡ ¡ a) b) Required displacement sensitivity ~ 3 * 10 -23 m/√Hz Demonstrated sensitivity ~ 5 * 10 -20 m/√Hz using Optomechanical sensor. Capacitive sensor using SQUID amplifiers.

Summary ¡ ¡ Offers advantage of spherical detection and wide bandwidth in an uncovered frequency band Requires advanced suspension and complicated construction Dual cylinder design gives up isotropic sensitivity but naturally supports ‘selective readout’ and simpler design Both require advances in optical transducers.

thank you!