Dual data driven SIMCA as a oneclassifier Alexey

Dual data driven SIMCA as a one-classifier Alexey Pomerantsev ICP RAS 20. 02. 14 WSC-9 1

One-classifier, e. g. SIMCA Target Alternative 20. 02. 14 WSC-9 2

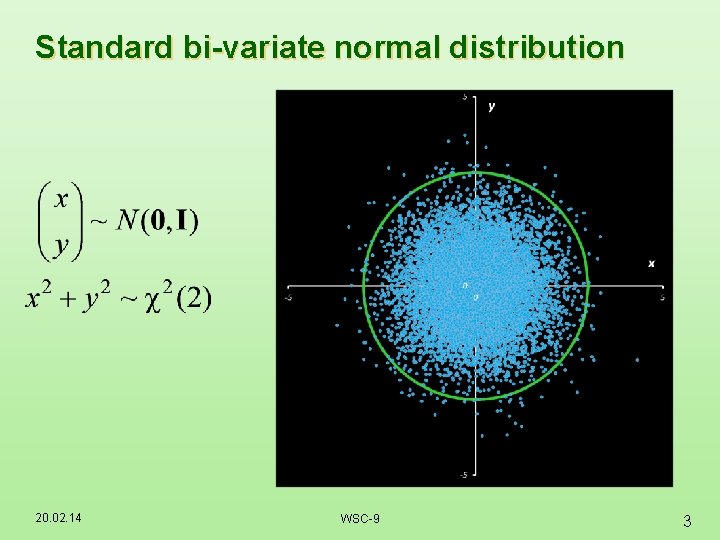
Standard bi-variate normal distribution 20. 02. 14 WSC-9 3

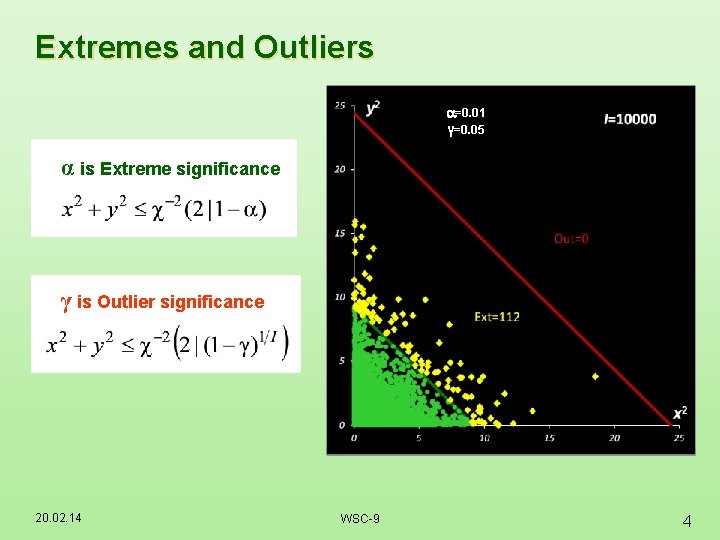
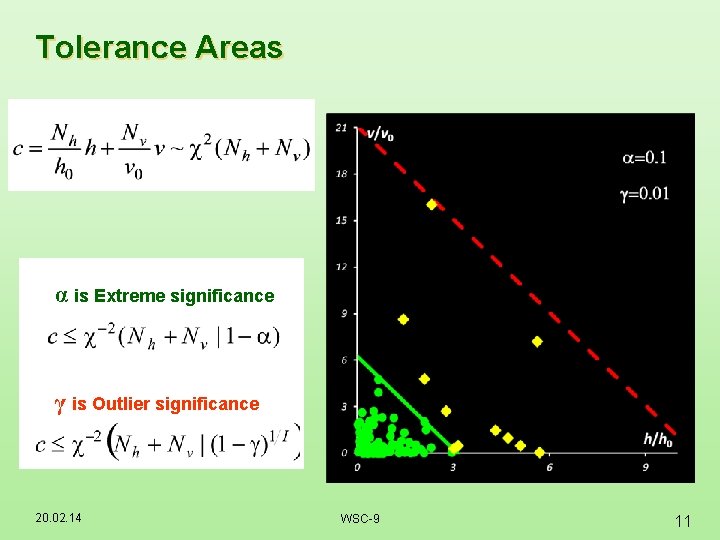
Extremes and Outliers =0. 01 γ=0. 05 α is Extreme significance γ is Outlier significance 20. 02. 14 WSC-9 4

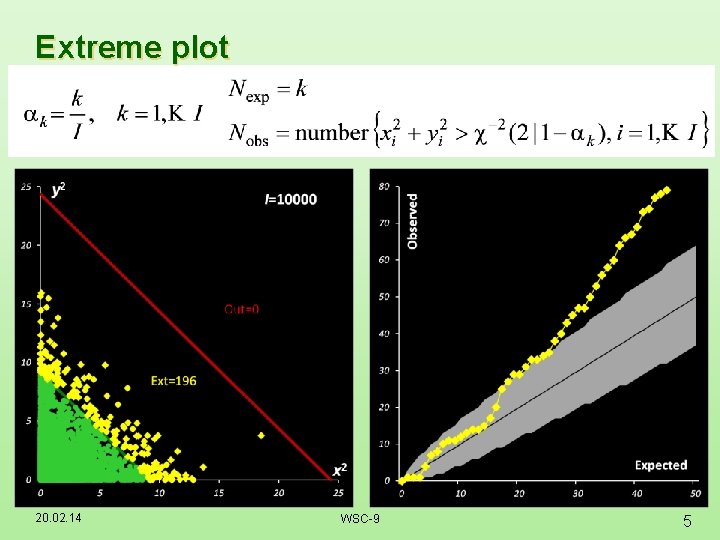
Extreme plot 20. 02. 14 WSC-9 5

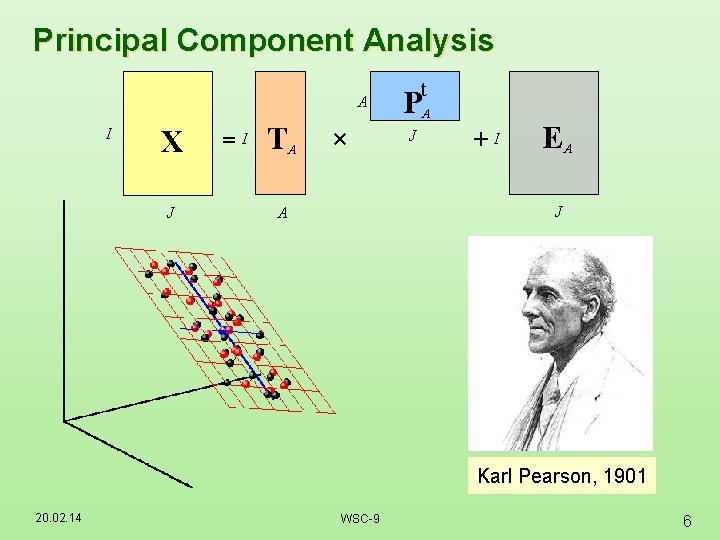
Principal Component Analysis A I X J =I TA × t PA J +I EA J A Karl Pearson, 1901 20. 02. 14 WSC-9 6

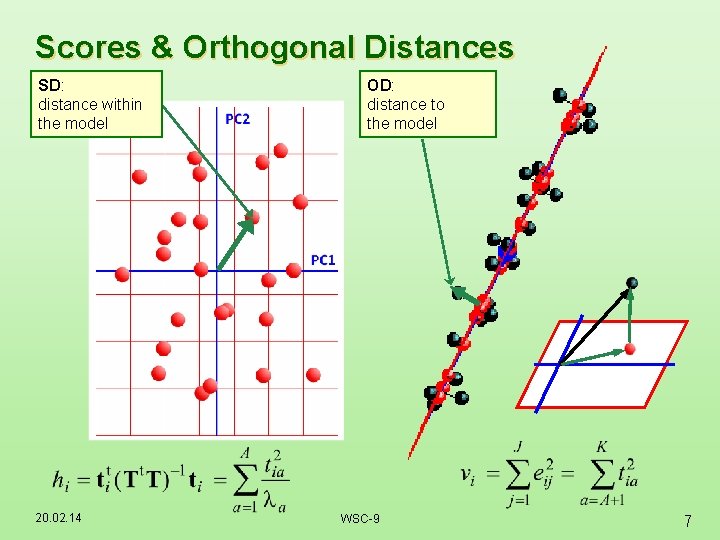
Scores & Orthogonal Distances SD: distance within the model 20. 02. 14 OD: distance to the model WSC-9 7

SD & OD distributions SD OD Westerhuis JA, Gurden SP, Smilde AK. Chemom. Intell. Lab. Syst. 2000; 51: 95– 114 De Braekeleer K, et al. Chemom. Intell. Lab. Syst. 1999; 46: 103– 116. Nomikos P, Mac. Gregor JF. Technometrics 1995; 37: 41– 59. 20. 02. 14 Pomerantsev A. J. Chemometrics, 2008, 22 : 601 -609 WSC-9 8

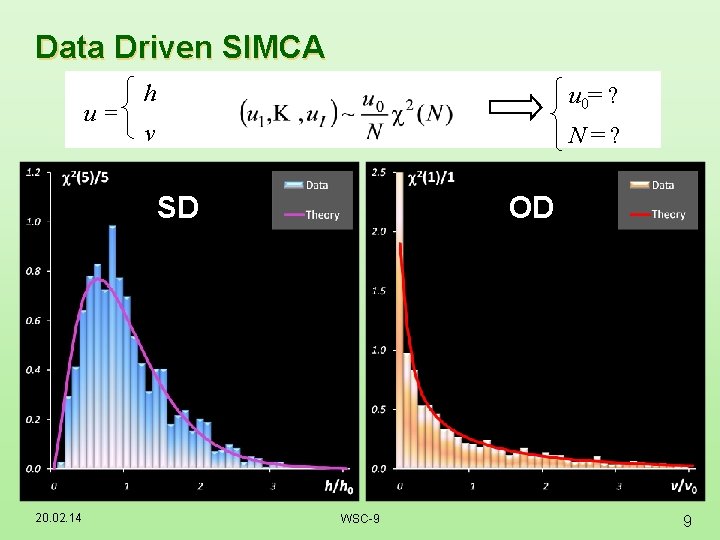
Data Driven SIMCA u= h u 0= ? v N=? SD 20. 02. 14 OD WSC-9 9

Total Distance Scores distance (SD) Orthogonal distance (OD) Total distance (TD) 20. 02. 14 WSC-9 10

Tolerance Areas α is Extreme significance γ is Outlier significance 20. 02. 14 WSC-9 11

Classical Data Driven (CDD) SIMCA Classical Method of Moments Given Then Where 20. 02. 14 WSC-9 12

Robust Data Driven (RDD) SIMCA Robust Method of Moments Given Then Where M=median(u) R=interquartile(u) ¼ ¼ u(1) ≤ u(2 )≤. . ≤ u(I-1) ≤ u(I) ½ 20. 02. 14 WSC-9 ½ 13

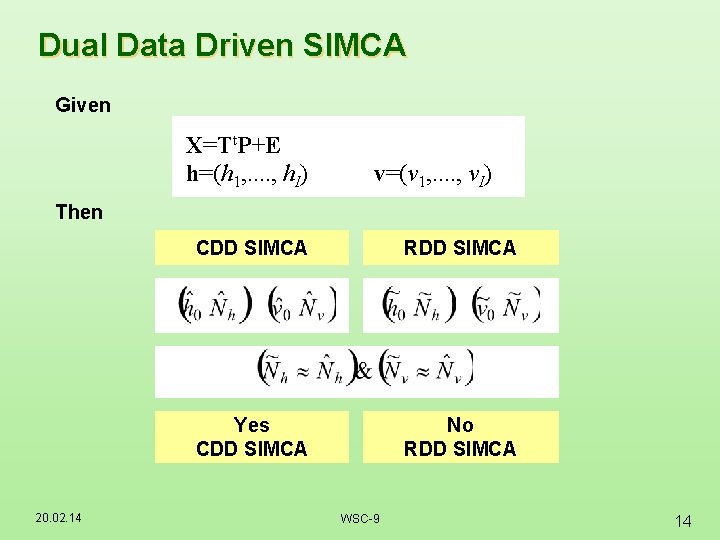
Dual Data Driven SIMCA Given X=Tt. P+E h=(h 1, . . , h. I) v=(v 1, . . , v. I) Then 20. 02. 14 CDD SIMCA RDD SIMCA Yes CDD SIMCA No RDD SIMCA WSC-9 14

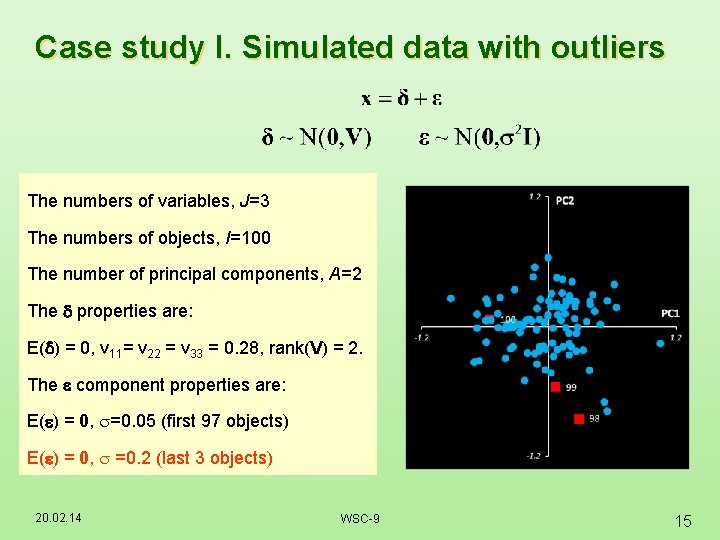
Case study I. Simulated data with outliers The numbers of variables, J=3 The numbers of objects, I=100 The number of principal components, A=2 The properties are: E( ) = 0, v 11= v 22 = v 33 = 0. 28, rank(V) = 2. The component properties are: E( ) = 0, =0. 05 (first 97 objects) E( ) = 0, =0. 2 (last 3 objects) 20. 02. 14 WSC-9 15

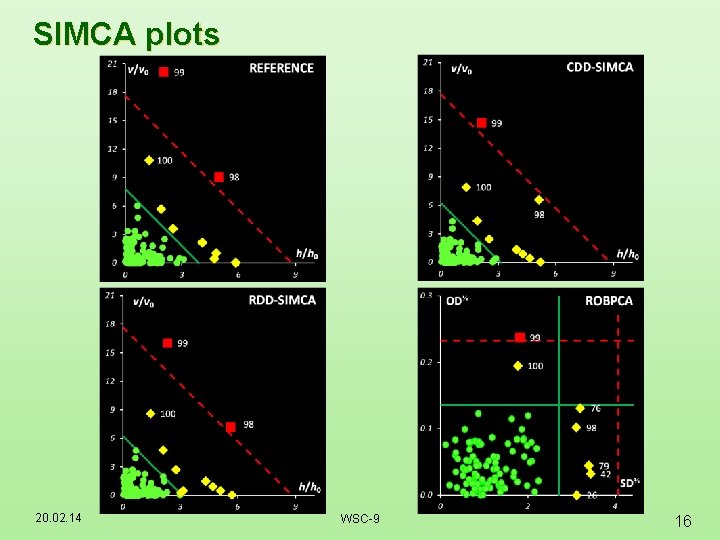
SIMCA plots 20. 02. 14 WSC-9 16

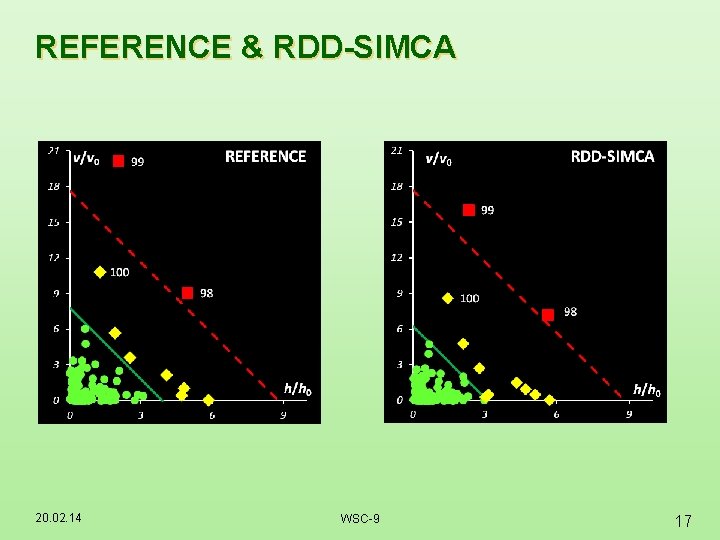
REFERENCE & RDD-SIMCA 20. 02. 14 WSC-9 17

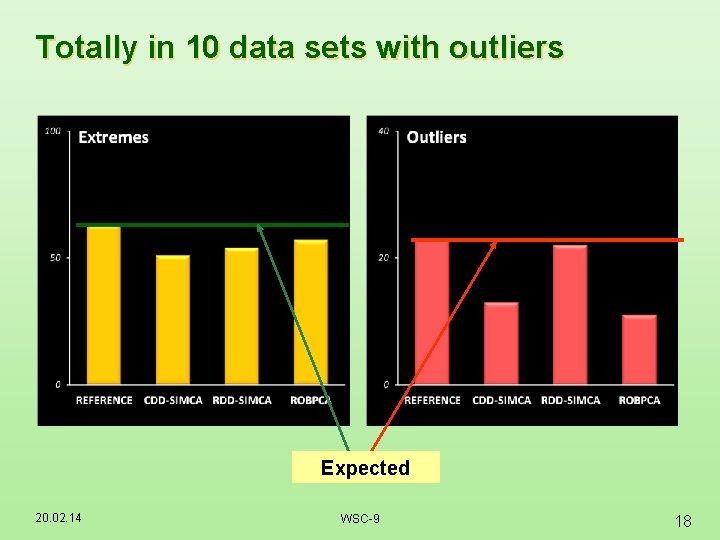
Totally in 10 data sets with outliers Expected 20. 02. 14 WSC-9 18

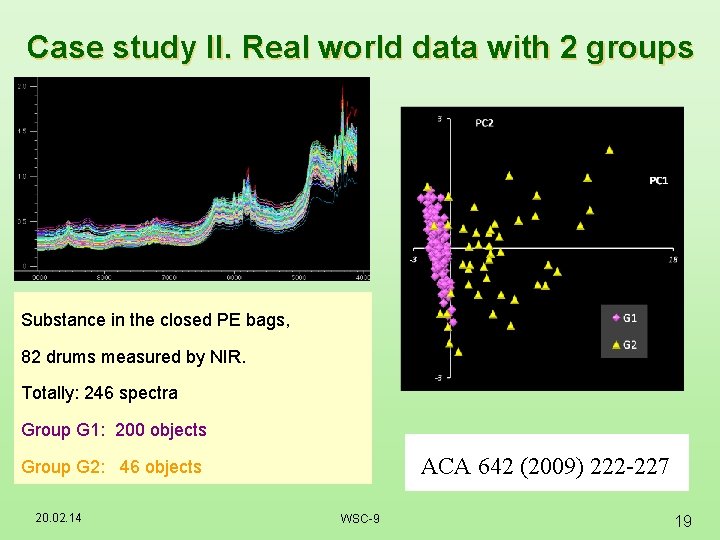
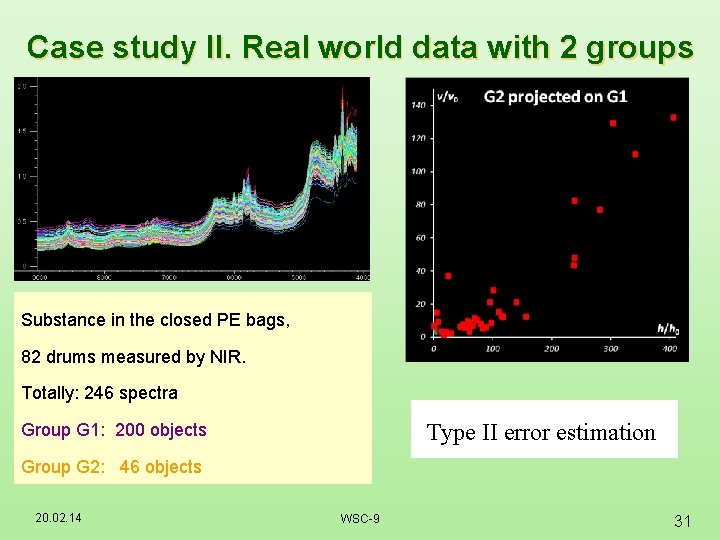
Case study II. Real world data with 2 groups Substance in the closed PE bags, 82 drums measured by NIR. Totally: 246 spectra Group G 1: 200 objects ACA 642 (2009) 222 -227 Group G 2: 46 objects 20. 02. 14 WSC-9 19

Probe position effect 20. 02. 14 WSC-9 20

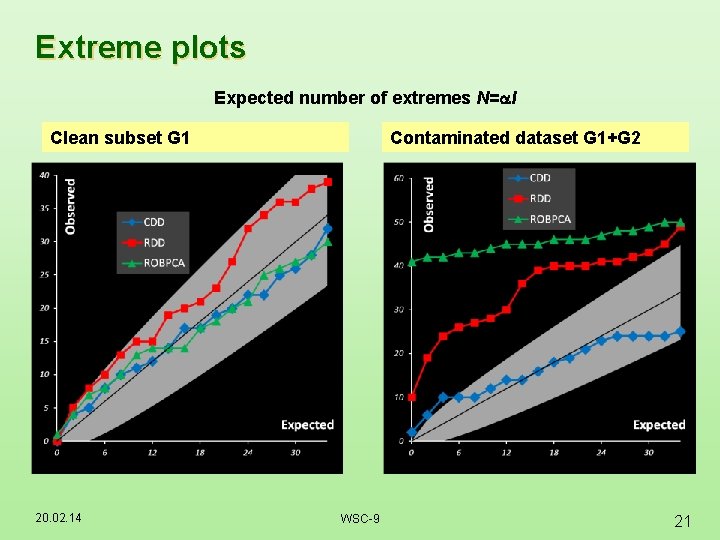
Extreme plots Expected number of extremes N= I Clean subset G 1 20. 02. 14 Contaminated dataset G 1+G 2 WSC-9 21

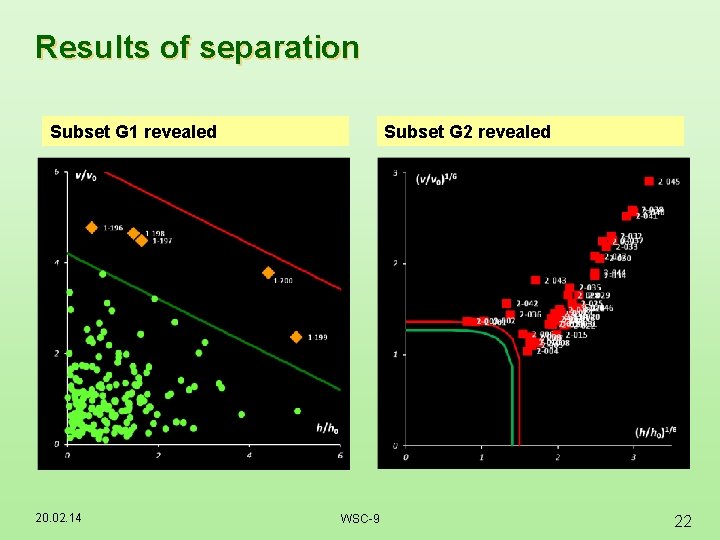
Results of separation Subset G 1 revealed 20. 02. 14 Subset G 2 revealed WSC-9 22

Reference 20. 02. 14 WSC-9 23

One-classification Type II error =1− Type I error Alternatives 20. 02. 14 WSC-9 24

How to find β in case AC is known Target Alternative 20. 02. 14 WSC-9 25

Two-classes discrimination: plums & apples mesh size ? 20. 02. 14 WSC-9 26

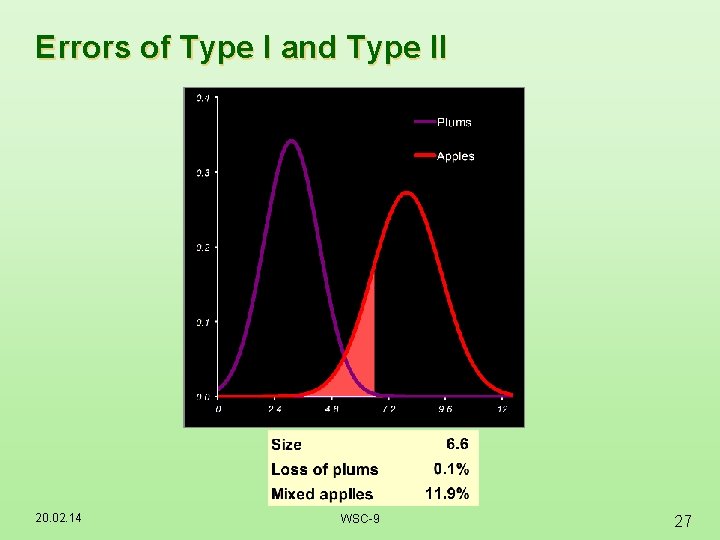
Errors of Type I and Type II 20. 02. 14 WSC-9 27

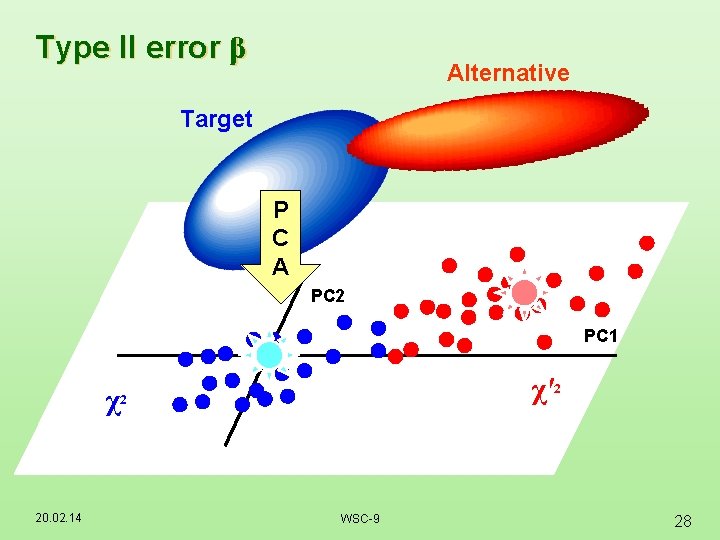
Type II error β Alternative Target P C A PC 2 PC 1 χ 20. 02. 14 χ'2 2 WSC-9 28

Non-central chi-squared distribution non-central chi-squared distribution the noncentrality parameter 20. 02. 14 WSC-9 29

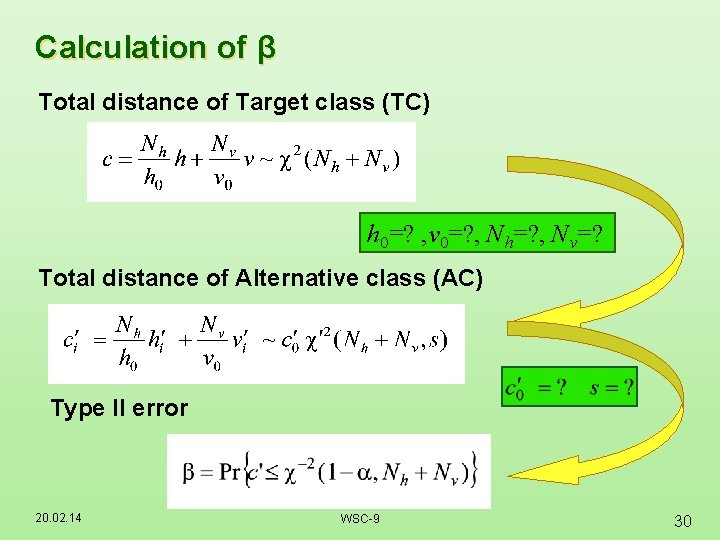
Calculation of β Total distance of Target class (TC) h 0=? , v 0=? , Nh=? , Nv=? Total distance of Alternative class (AC) Type II error 20. 02. 14 WSC-9 30

Case study II. Real world data with 2 groups Substance in the closed PE bags, 82 drums measured by NIR. Totally: 246 spectra Type II error estimation Group G 1: 200 objects Group G 2: 46 objects 20. 02. 14 WSC-9 31

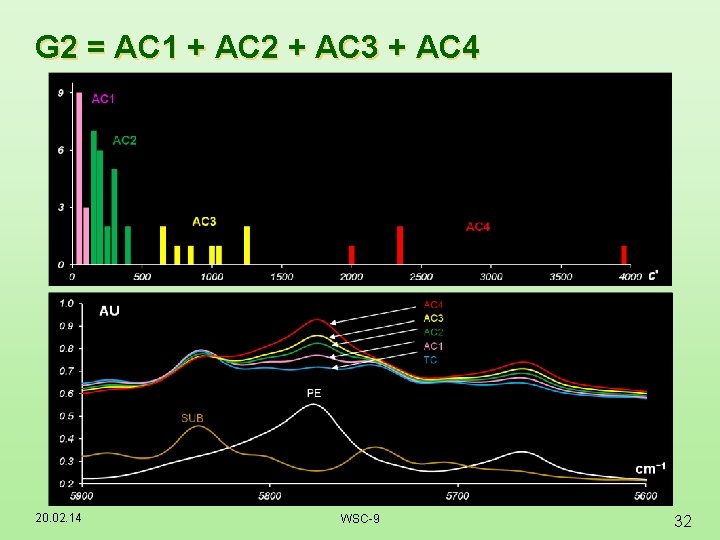
G 2 = AC 1 + AC 2 + AC 3 + AC 4 20. 02. 14 WSC-9 32

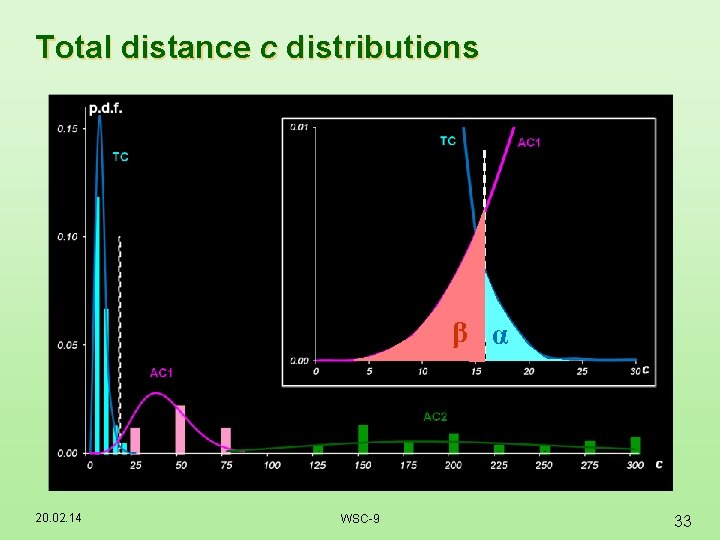
Total distance c distributions β α 20. 02. 14 WSC-9 33

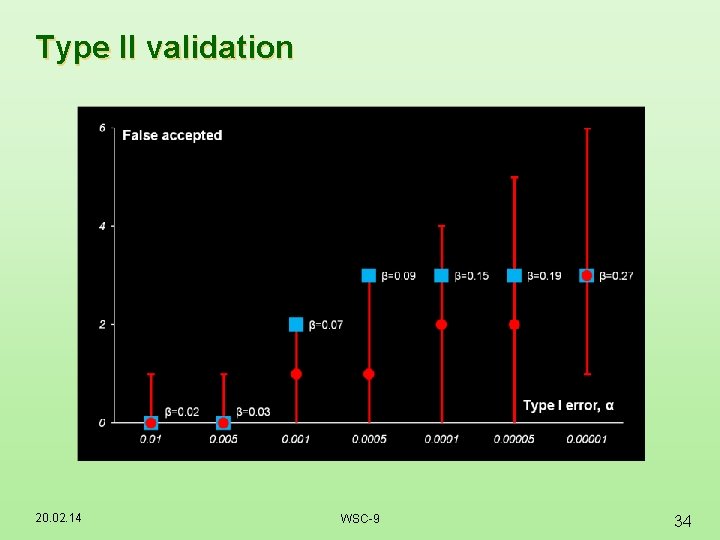
Type II validation 20. 02. 14 WSC-9 34

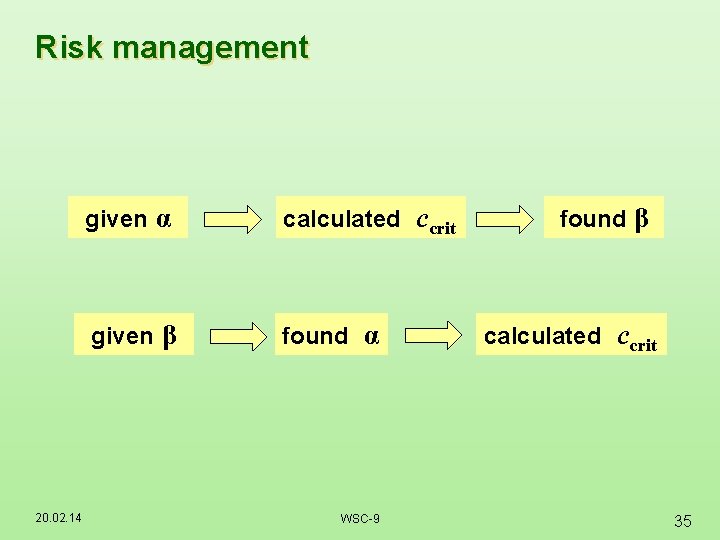
Risk management 20. 02. 14 given α calculated ccrit given β found α WSC-9 found β calculated ccrit 35

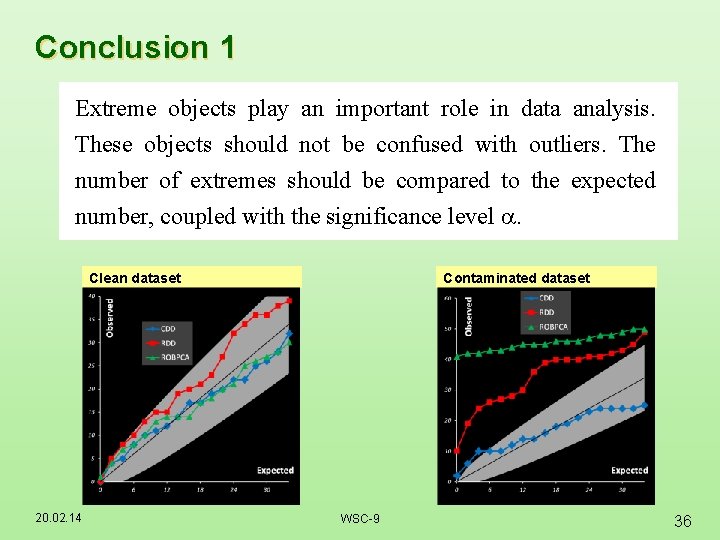
Conclusion 1 Extreme objects play an important role in data analysis. These objects should not be confused with outliers. The number of extremes should be compared to the expected number, coupled with the significance level . Clean dataset 20. 02. 14 Contaminated dataset WSC-9 36

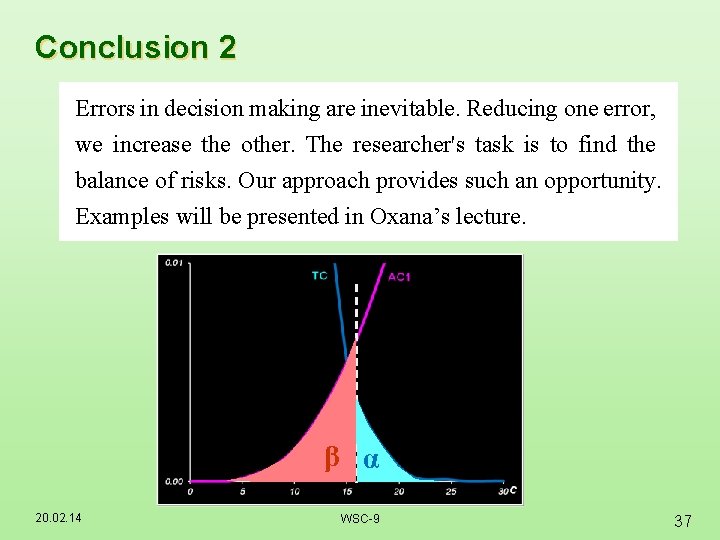
Conclusion 2 Errors in decision making are inevitable. Reducing one error, we increase the other. The researcher's task is to find the balance of risks. Our approach provides such an opportunity. Examples will be presented in Oxana’s lecture. β α 20. 02. 14 WSC-9 37

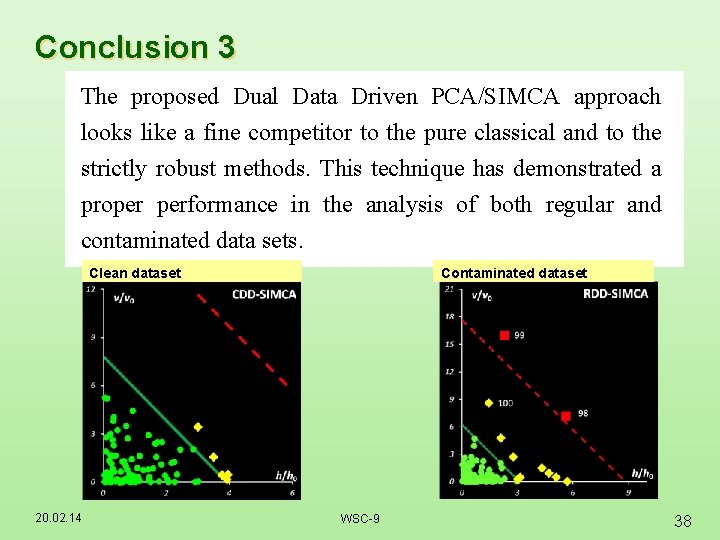
Conclusion 3 The proposed Dual Data Driven PCA/SIMCA approach looks like a fine competitor to the pure classical and to the strictly robust methods. This technique has demonstrated a proper performance in the analysis of both regular and contaminated data sets. Clean dataset 20. 02. 14 Contaminated dataset WSC-9 38

Thank you for your attention A Lawyer’s Mistake 20. 02. 14 WSC-9 39