DTC Quantitative Methods Regression I Correlation and Linear

DTC Quantitative Methods Regression I: (Correlation and) Linear Regression Thursday 7 th March 2013

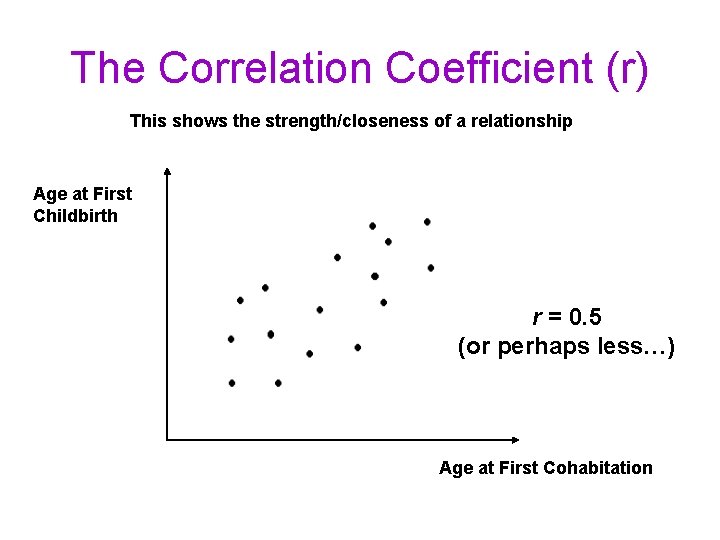
The Correlation Coefficient (r) This shows the strength/closeness of a relationship Age at First Childbirth r = 0. 5 (or perhaps less…) Age at First Cohabitation

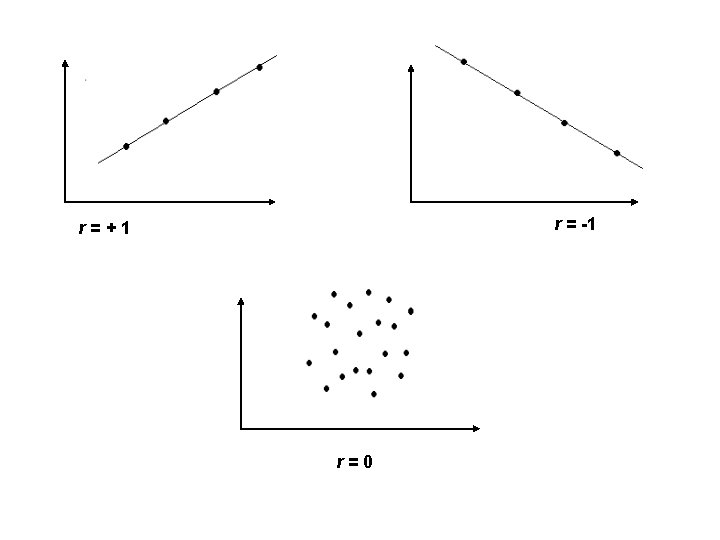
Correlation… and Regression • r measures correlation in a linear way • … and is connected to linear regression • More precisely, it is r 2 (r-squared) that is of relevance • It is the ‘variation explained’ by the regression line • … and is sometimes referred to as the ‘coefficient of determination’

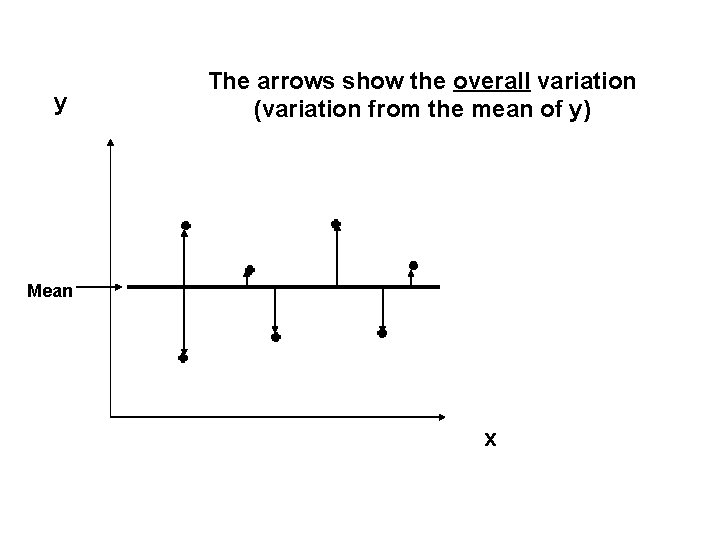
y The arrows show the overall variation (variation from the mean of y) Mean x

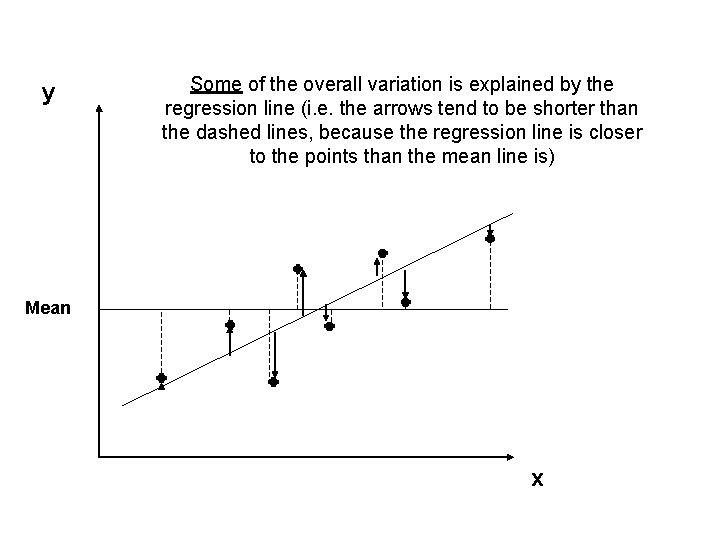
y Some of the overall variation is explained by the regression line (i. e. the arrows tend to be shorter than the dashed lines, because the regression line is closer to the points than the mean line is) Mean x

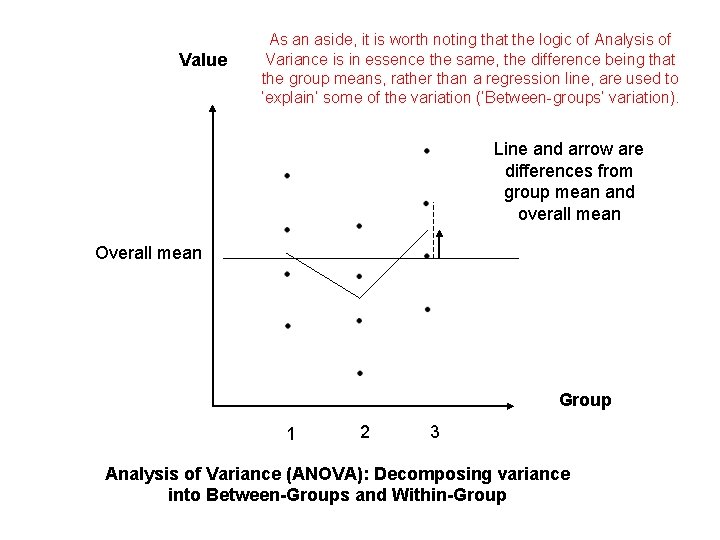
Value As an aside, it is worth noting that the logic of Analysis of Variance is in essence the same, the difference being that the group means, rather than a regression line, are used to ‘explain’ some of the variation (‘Between-groups’ variation). Line and arrow are differences from group mean and overall mean Overall mean Group 1 2 3 Analysis of Variance (ANOVA): Decomposing variance into Between-Groups and Within-Group

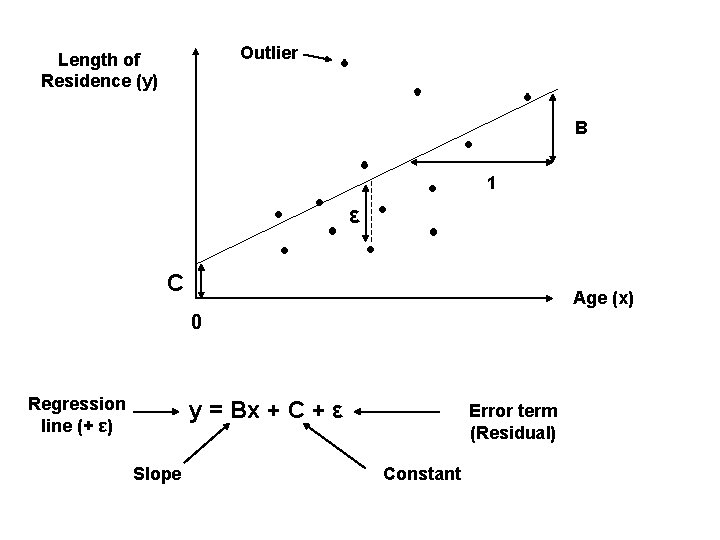
Outlier Length of Residence (y) B 1 ε C Age (x) 0 Regression line (+ ε) y = Bx + C + ε Slope Error term (Residual) Constant

Choosing the line that best explains the data • Some variation is explained by the regression line • The residuals constitute the unexplained variation • The regression line is chosen so as to minimise the sum of the squared residuals • i. e. to minimise Σε 2 (Σ means ‘sum of’) • The full/specific name for this technique is Ordinary Least Squares (OLS) linear regression

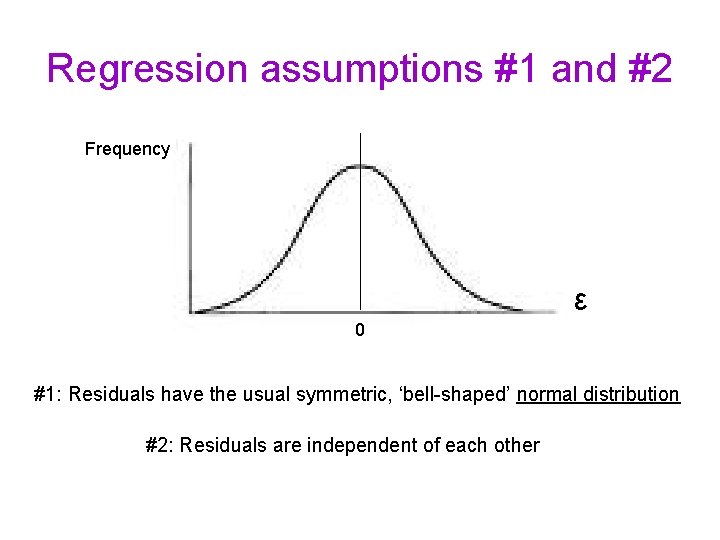
Regression assumptions #1 and #2 Frequency ε 0 #1: Residuals have the usual symmetric, ‘bell-shaped’ normal distribution #2: Residuals are independent of each other

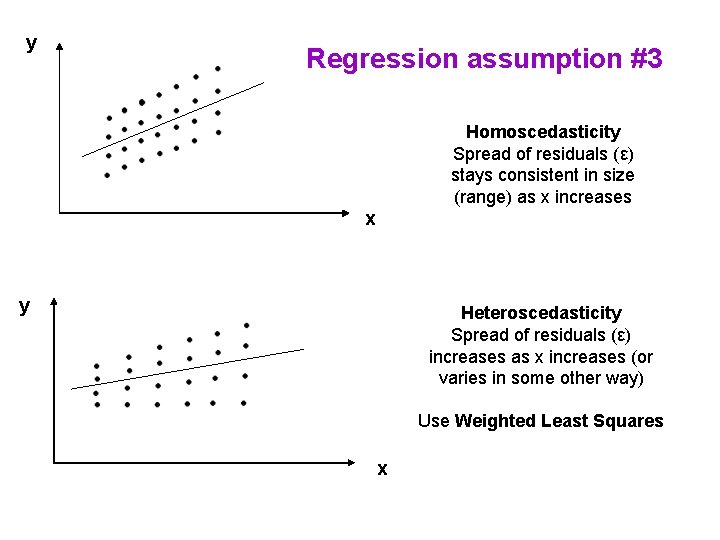
y Regression assumption #3 Homoscedasticity Spread of residuals (ε) stays consistent in size (range) as x increases x y Heteroscedasticity Spread of residuals (ε) increases as x increases (or varies in some other way) Use Weighted Least Squares x

Regression assumption #4 • Linearity! (We’ve already assumed this…) • In the case of a nonlinear relationship, one may be able to use a non-linear regression equation, such as: y = B 1 x + B 2 x 2 + c

Another problem: Multicollinearity • If two ‘independent variables’, x and z, are perfectly correlated (i. e. identical), it is impossible to tell what the B values corresponding to each should be • e. g. if y = 2 x + c, and we add z, should we get: • y = 1. 0 x + 1. 0 z + c, or • y = 0. 5 x + 1. 5 z + c, or • y = -5001. 0 x + 5003. 0 z + c ? • The problem applies if two variables are highly (but not perfectly) correlated too…

Example of Regression (from Pole and Lampard, 2002, Ch. 9) • GHQ = (-0. 69 x INCOME) + 4. 94 • Is -0. 69 significantly different from 0 (zero)? • A test statistic that takes account of the ‘accuracy’ of the B of -0. 69 (by dividing it by its standard error) is t = -2. 142 • For this value of t in this example, the significance value is p = 0. 038 < 0. 05 • r-squared here is (-0. 321)2 = 0. 103 = 10. 3%

B’s and Multivariate Regression Analysis • The impact of an independent variable on a dependent variable is B • But how and why does the value of B change when we introduce another independent variable? • If the effects of the two independent are inter-related in the sense that they interact (i. e. the effect of one depends on the value of the other), how does B vary?

Multiple Regression • GHQ = (-0. 47 x INCOME) + (-1. 95 x HOUSING) + 5. 74 • For B = 0. 47, t = -1. 51 (& p = 0. 139 > 0. 05) • For B = -1. 95, t = -2. 60 (& p = 0. 013 < 0. 05) • The r-squared value for this regression is 0. 236 (23. 6%)

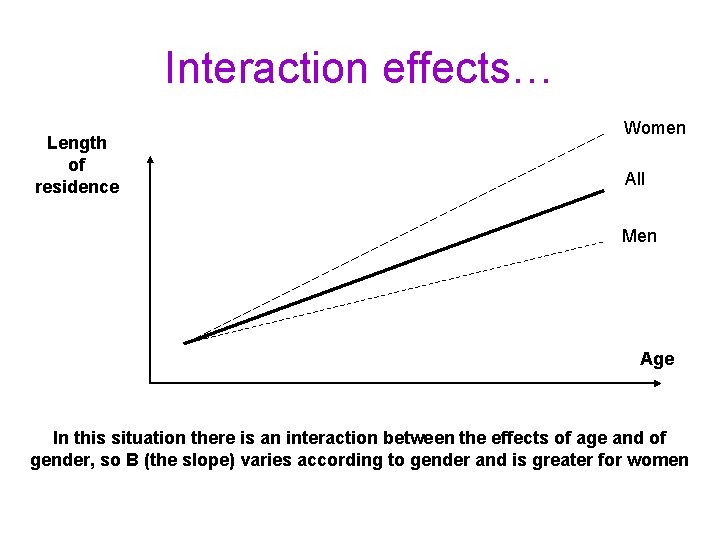
Interaction effects… Length of residence Women All Men Age In this situation there is an interaction between the effects of age and of gender, so B (the slope) varies according to gender and is greater for women

Dummy variables • Categorical variables can be included in regression analyses via the use of one or more dummy variables (two-category variables with values of 0 and 1). • In the case of a comparison of men and women, a dummy variable could compare men (coded 1) with women (coded 0).

Creating a variable to check for an interaction effect • We may want to see whether an effect varies according to the level of another variable. • Multiplying the values of two independent variables together, and including this third variable alongside the other two allows us to do this.

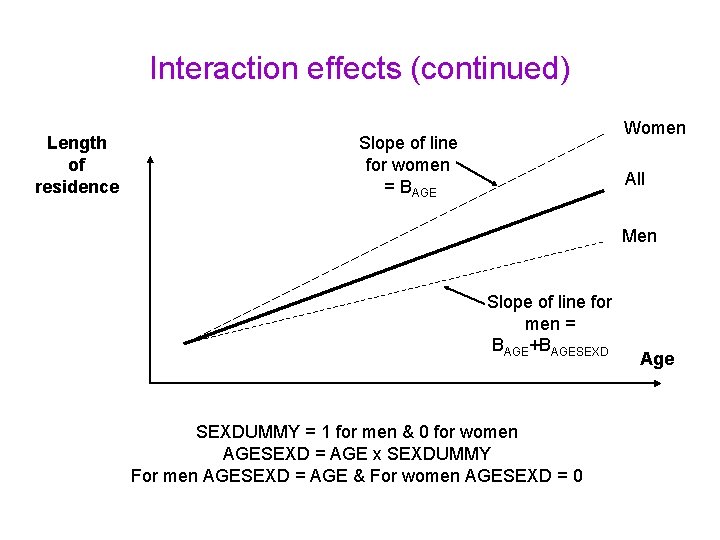
Interaction effects (continued) Length of residence Women Slope of line for women = BAGE All Men Slope of line for men = BAGE+BAGESEXDUMMY = 1 for men & 0 for women AGESEXD = AGE x SEXDUMMY For men AGESEXD = AGE & For women AGESEXD = 0 Age