DSS for Integrated Water Resources Management IWRM IWRM

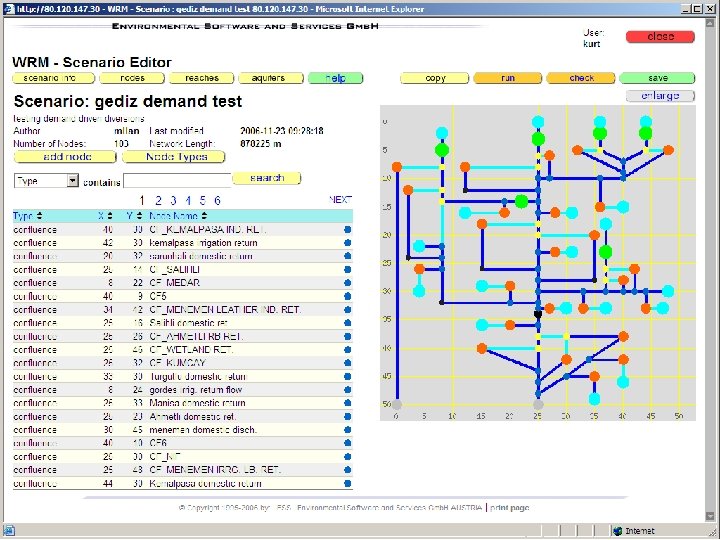
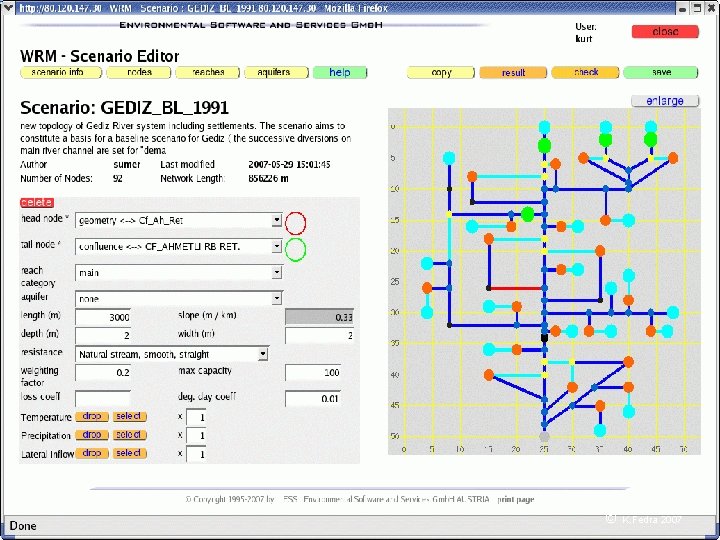
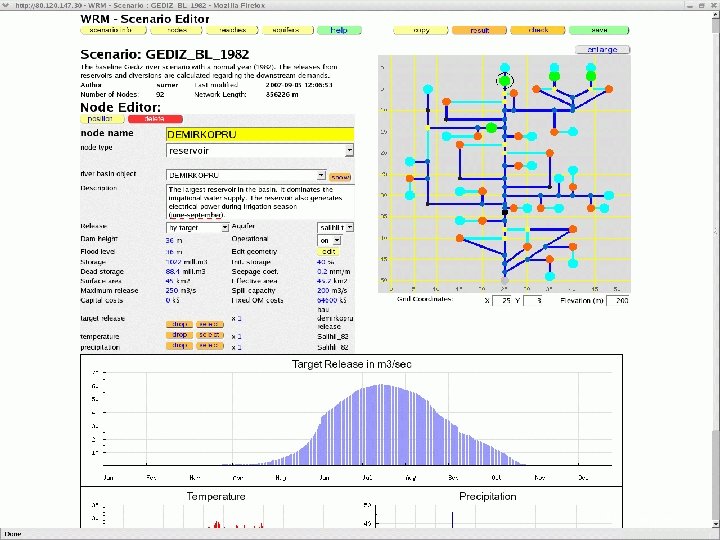
DSS for Integrated Water Resources Management (IWRM) IWRM model representation, scenarios, optimization DDr. Kurt Fedra ESS Gmb. H, Austria kurt@ess. co. at http: //www. ess. co. at Environmental Software & Services A-2352 Gumpoldskirchen 1 © K. Fedra 2007

Main topics: model representation of river basin and water resources: • conservation laws, • hydrological cycle, precipitation, EVT, • Basin topology: cascading reservoirs, routing, GW • water quality; 2 © K. Fedra 2007

IWRM: what to decide ? • Water allocation (sectoral: agriculture, domestic, industrial, recreational, environmental (dilution ? ), hydropower, shipping, or geographic: upstream/downstream) • Waste allocation: permitting, emission standards, treatment • Development projects (investment) • Strategic planning: regional/national development, security, sustainability (climate change) 3 © K. Fedra 2007

Decision support paradigms • Information systems (menu of options) • Scenario analysis (and comparison) WHAT IF • Rational maximization HOW TO (reach objectives), optimization 4 © K. Fedra 2007

DSS structure: Analytical core: • • Design of alternatives Assessment and evaluation, alternatives WHY Model based analysis: • Impossible to experiment in the real world (costs) • Impossible to try enough alternatives (time) 5 © K. Fedra 2007

Model representation Conservation laws: Mass conservation, mass budget inputs - output - storage change = 0 Water is neither generated nor lost within the system, but can change state (evaporation, ice) or be incorporated into products (crops, beverages). 6 © K. Fedra 2007

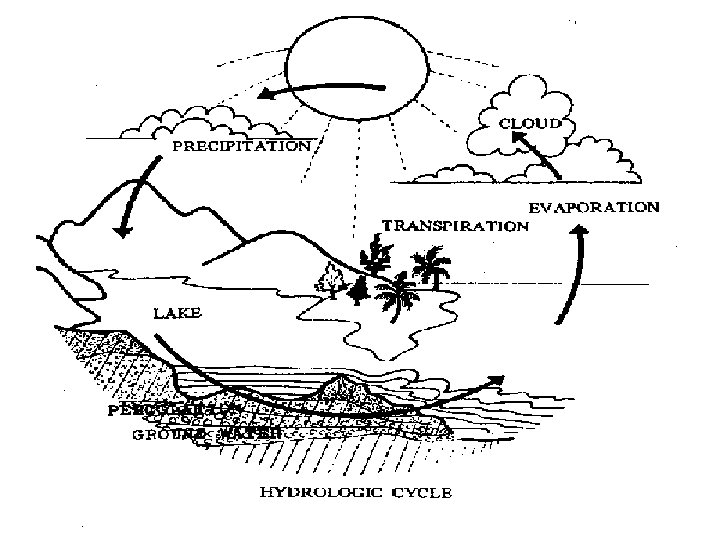
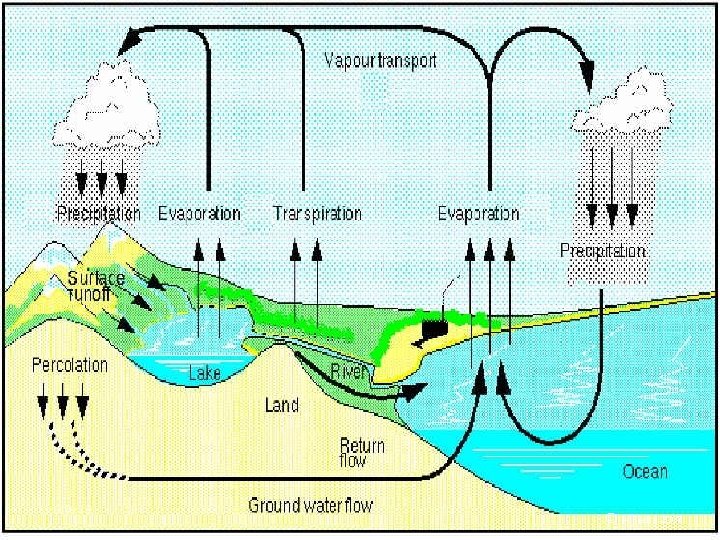
Model representation Hydrological Cycle: Water evaporates from land sea, precipitates, evaporates, forms runoff, gets stored, diverted and/or used (consumptive use), percolates into groundwater. 7 © K. Fedra 2007

8 © K. Fedra 2007

9 © K. Fedra 2007

10 © K. Fedra 2007

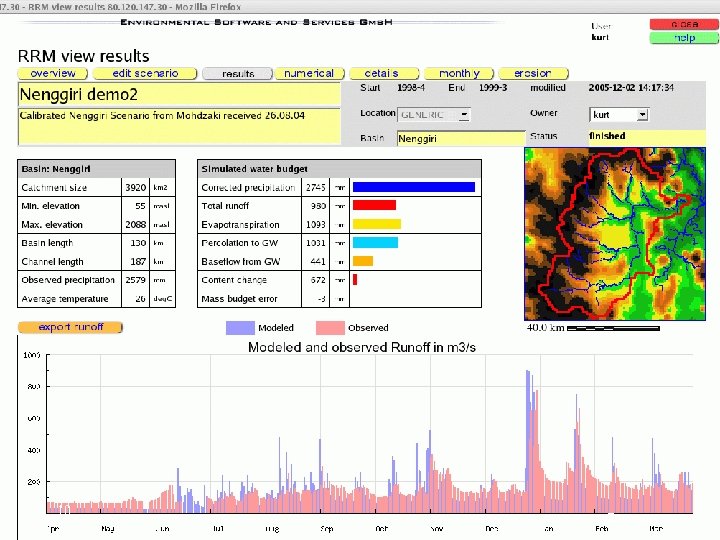
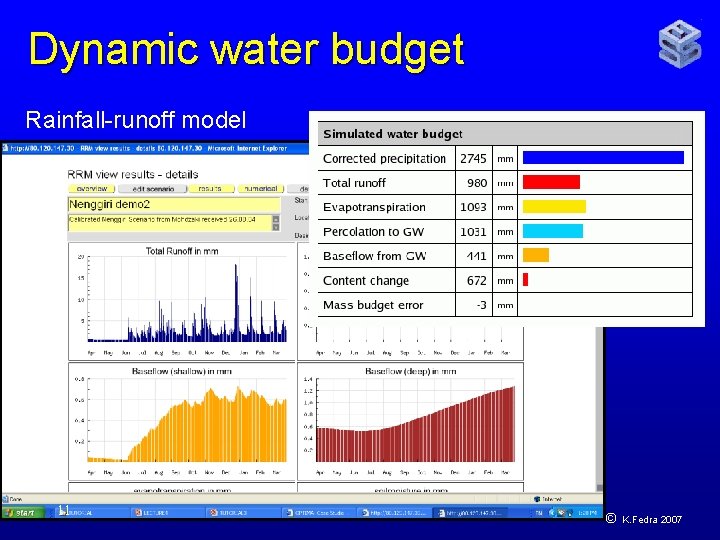
Dynamic water budget Rainfall-runoff model 11 © K. Fedra 2007

Model representation Precipitation: • THE key variable == input • High variability in time and space (synoptic observation: weather radar) • High measurement error large uncertainties 12 © K. Fedra 2007

Model representation Evapotranspiration • Evaporation: phase change from liquid to gaseous, function of temperature and vapour pressure • Transpiration: physiological vapour production by plants (evaporation from stomata, and animals in respiration ) 13 © K. Fedra 2007

Model representation Evaporation: Penman-Monteith 14 © K. Fedra 2007

Penman-Monteith where: Rn is the net radiation, G is the soil heat flux, (es - ea) represents the vapour pressure deficit of the air, ra is the mean air density at constant pressure, cp is the specific heat of the air, Δ represents the slope of the saturation vapour pressure temperature relationship, γ is the psychrometric constant, rs and ra are the (bulk) surface and aerodynamic resistances. 15 © K. Fedra 2007

Evapotranspiration Simple practical method: • Degree day method: EVTP = a * avg. air Temperature a is in the order of 0. 1 mm/o. K varies with land cover/vegetation and humidity, wind exposure 16 © K. Fedra 2007

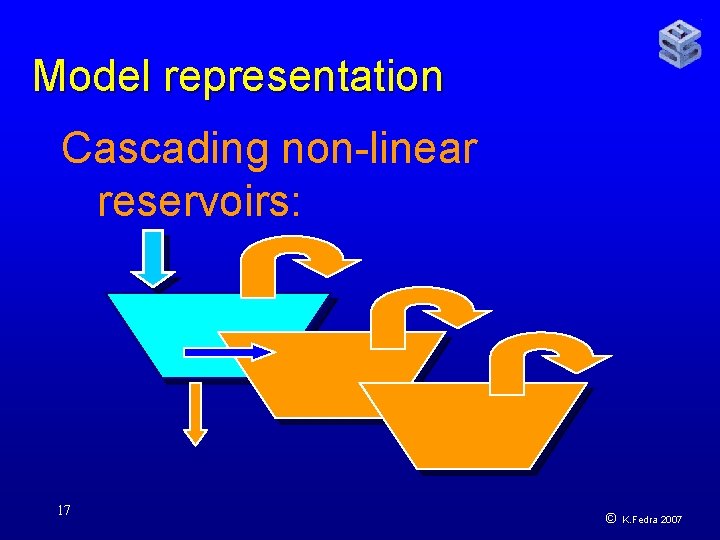
Model representation Cascading non-linear reservoirs: 17 © K. Fedra 2007

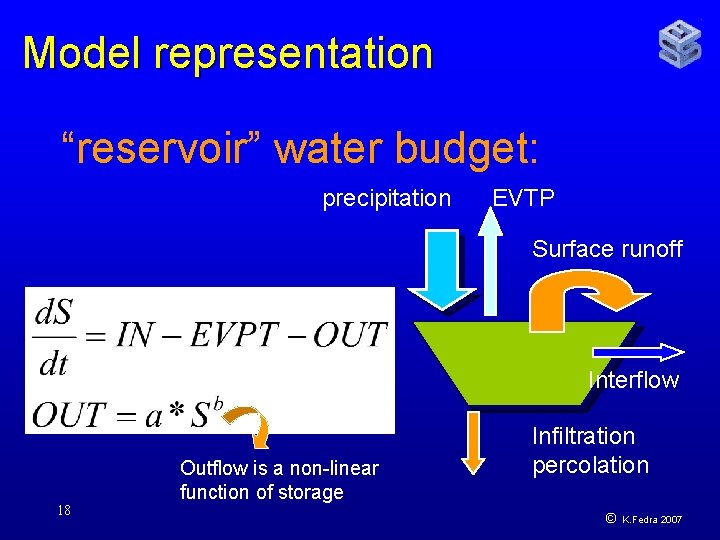
Model representation “reservoir” water budget: precipitation EVTP Surface runoff Interflow 18 Outflow is a non-linear function of storage Infiltration percolation © K. Fedra 2007

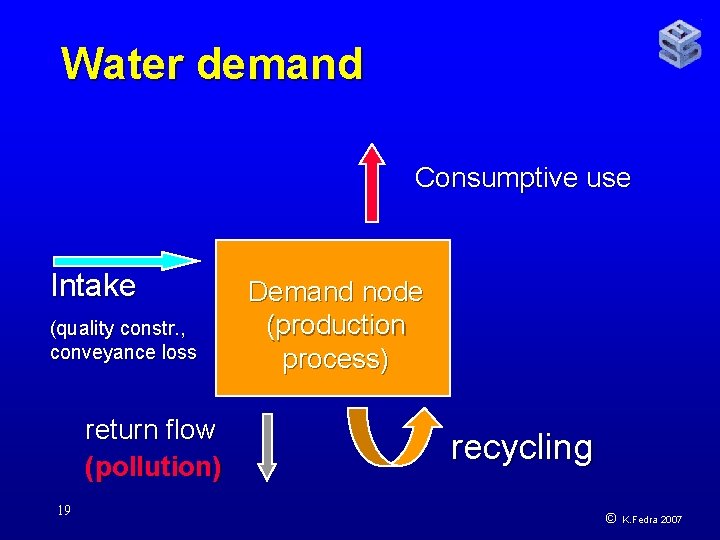
Water demand Consumptive use Intake (quality constr. , conveyance loss return flow (pollution) 19 Demand node (production process) recycling © K. Fedra 2007

Model representation Runoff of excess storage that exceeds the “reservoir” capacity: • from canopy (interception storage) • soil surface (exceeding infiltration capacity Hortonian sheet flow, flash floods) • Unsaturated zone: – horizontal interflow – vertical percolation (> field capacity) • Saturated zone: Darcy flow of groundwater, f of head difference and conductivity 20 © K. Fedra 2007

Model representation Navier-Stokes equations: 21 © K. Fedra 2007

Navier-Stokes Equations Divergence: 22 Kronecker Delta © K. Fedra 2007

Model representation Open channel flow: The empirical Manning formula states: where: – – 23 V is the cross-sectional average velocity (m/s) n is the Manning coefficient of roughness (0. 01 – 0. 075) Rh is the hydraulic radius (m) S is the slope of the water surface or the linear hydraulic head loss (m/m) (S = hf / L) © K. Fedra 2007

Model representation Hydraulic radius: Rh part of the channels resistance that controls speed of flow: A: cross section P: wetted perimeter P=b+c+d 24 © K. Fedra 2007

Reaches 25 © K. Fedra 2007

Channel Flow Routing Muskingum routing: S = K [ x. I + ( 1 - x ) O ] where S I O K X 26 = reach storage = inflow rate = outflow rate = storage parameter (~ travel time) = storage parameter (0 - 0. 5, describes attenuation) © K. Fedra 2007

Model representation Groundwater Laminar flow (Darcy) depends on • elevation difference (gravity) • conductivity (resistance) • cross-sectional area 27 © K. Fedra 2007

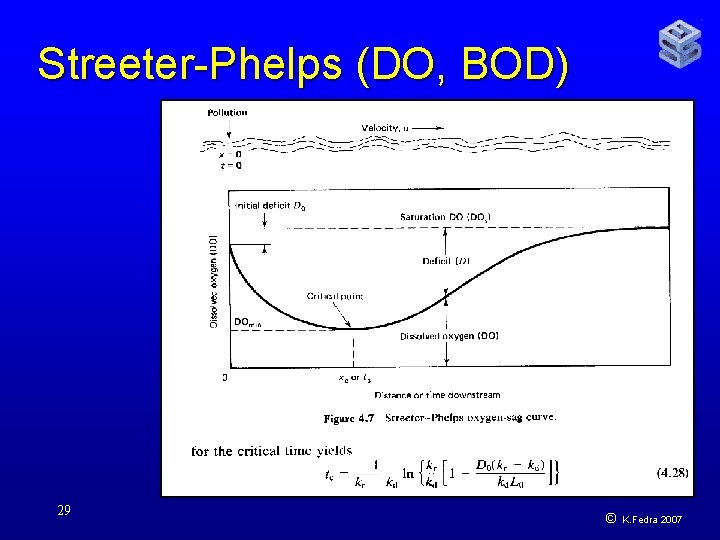
Model representation Water quality: • BOD/DO (Streeter-Phelps) • Nutrients (fertilizer, NO 3 in GW) • Agrochemicals (toxic, persistent, bioaccumulating) • Heavy metals (industrial waste) • Turbidity, sediments, erosion, siltation • Water borne diseases 28 © K. Fedra 2007

Streeter-Phelps (DO, BOD) 29 © K. Fedra 2007

Streeter-Phelps (DO, BOD) 30 © K. Fedra 2007

Streeter-Phelps (DO, BOD) 31 © K. Fedra 2007

Streeter-Phelps (DO, BOD) 32 © K. Fedra 2007

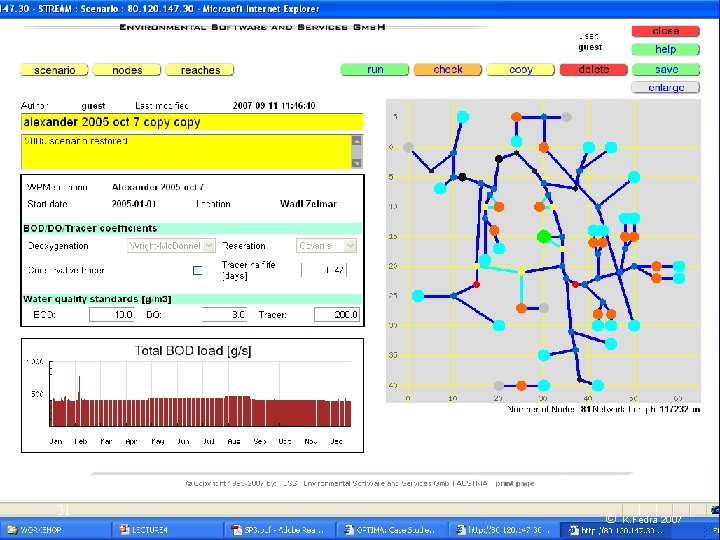
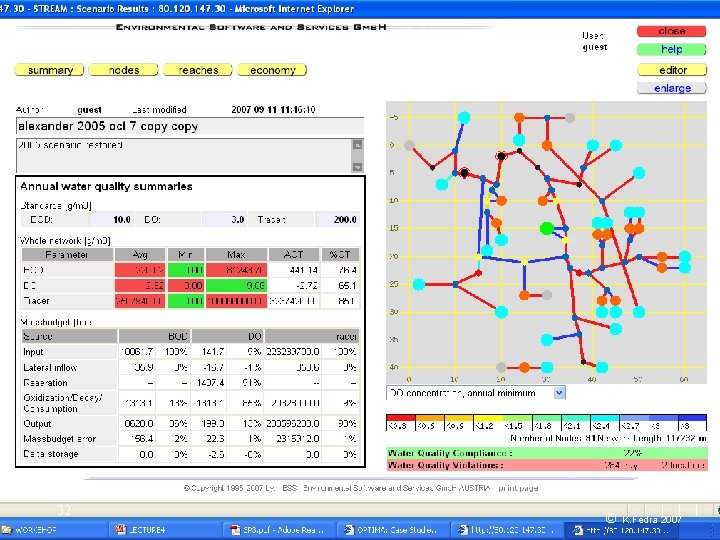
Model representation Data requirements • Physiography • Hydro-meteorology • Drainage network, structures • Demand areas (nodes) • Pollution sources • Techno-economics 33 © K. Fedra 2007

Multi criteria optimization 34 © K. Fedra 2007

35 © K. Fedra 2007

Reaches 36 © K. Fedra 2007

37 © K. Fedra 2007

Model purpose Structure the problem: • WHAT FOR (purpose) Questions to be answered ? Identify gaps in understanding Define data requirements Define validation strategy 38 © K. Fedra 2007

Model purpose WHAT FOR, WHY (not how) • Model is a TOOL for purpose • No BEST model (or hammer …) • Choice of model and data requirements depend on the QUESTION to be answered 39 © K. Fedra 2007

Modeling and DSS MOST IMPORTANT: ask good questions (that can be answered to support decisions) Model application is an experiment, hypothesis testing: does it make sense, does it add up ? Multiple models (agreement ? ) 40 © K. Fedra 2007