DSM Design Structure Matrix Prof Yoram Reich Arie

DSM Design Structure Matrix Prof. Yoram Reich & Arie Karniel School of Mechanical Engineering Faculty of Engineering Tel Aviv University Copyright © 2005 Reich This presentation includes material copyrighted by others. Please do not distribute. Copyright © 2003 -2005 Yoram Reich

Complexity of systems Copyright © 2003 -2005 Yoram Reich 2

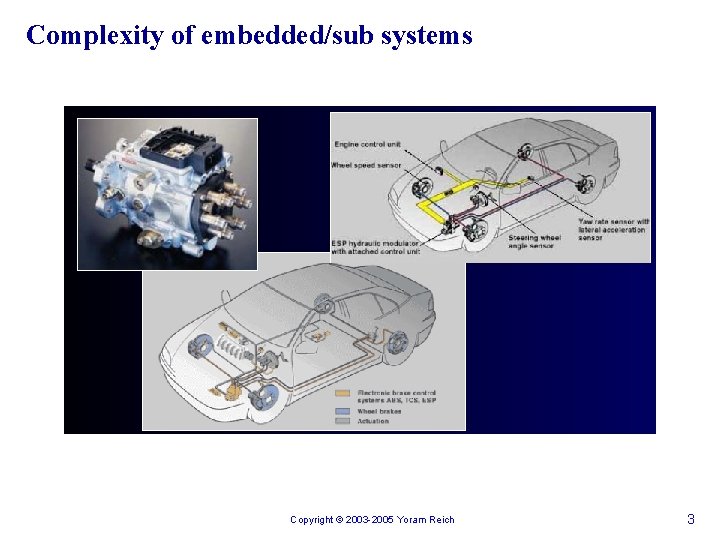
Complexity of embedded/sub systems Copyright © 2003 -2005 Yoram Reich 3

Complexity of an engine n n n n n n Engine block Pistons Connecting rods Crankshaft Flywheel Lubrication Heads Camshaft/Valve Train Cooling Intake manifold Fuel system Accessory drive Air cleaner A. I. R. Throttle body Exhaust BGR EVAP Ignition PCM Engine electrical Engine assembly Copyright © 2003 -2005 Yoram Reich 4

More Complexity … n n Complexity of teams/organizations required to design complex products Complexity of processes Complexity of the details of decisions that need to be coordinated to complete design … Copyright © 2003 -2005 Yoram Reich 5

Managing complexity n n n We need a tool for modeling the complexity , analyzing it, and using the results to improve practice Copyright © 2003 -2005 Yoram Reich 6

DSM – Design Structure Matrix n Next generation of PM Tools u u u 1900 s gave us Gantt 1960 s gave us CPM/PERT 1990 s gives us DSM n Early work be Steward and Warfield n Focuses on information flow rather than on activity flow! n n Incorporates loops and feedback Visually appealing Mathematical structure: binary matrices Methodology for different algorithms: u Partitioning, clustering, banding Copyright © 2003 -2005 Yoram Reich 7

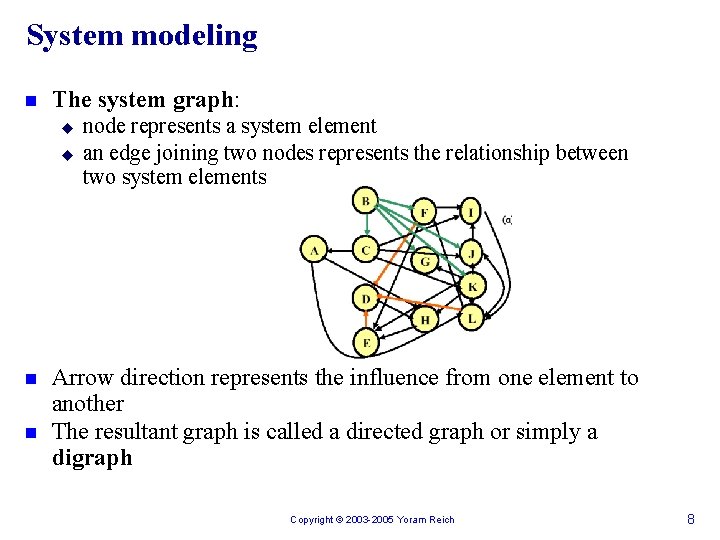
System modeling n The system graph: u u n n node represents a system element an edge joining two nodes represents the relationship between two system elements Arrow direction represents the influence from one element to another The resultant graph is called a directed graph or simply a digraph Copyright © 2003 -2005 Yoram Reich 8

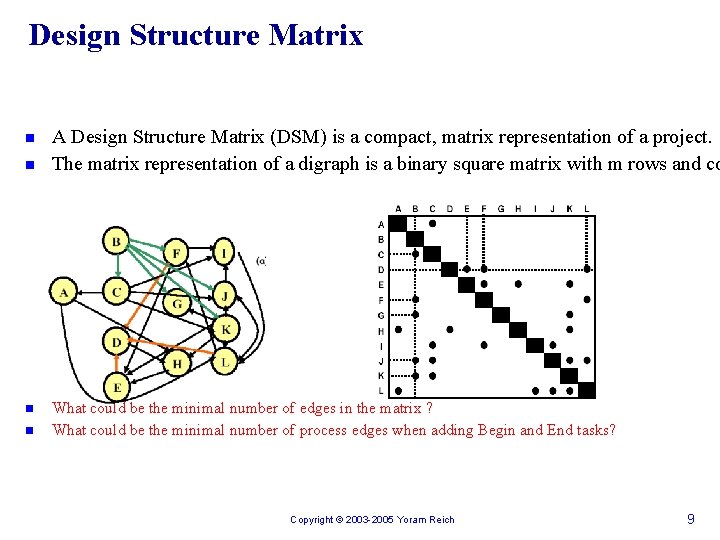
Design Structure Matrix n n A Design Structure Matrix (DSM) is a compact, matrix representation of a project. The matrix representation of a digraph is a binary square matrix with m rows and co What could be the minimal number of edges in the matrix ? What could be the minimal number of process edges when adding Begin and End tasks? Copyright © 2003 -2005 Yoram Reich 9

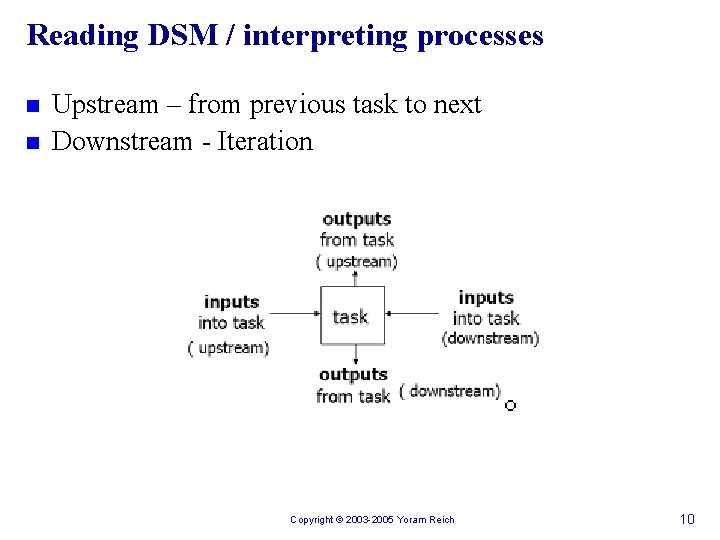
Reading DSM / interpreting processes n n Upstream – from previous task to next Downstream - Iteration Copyright © 2003 -2005 Yoram Reich 10

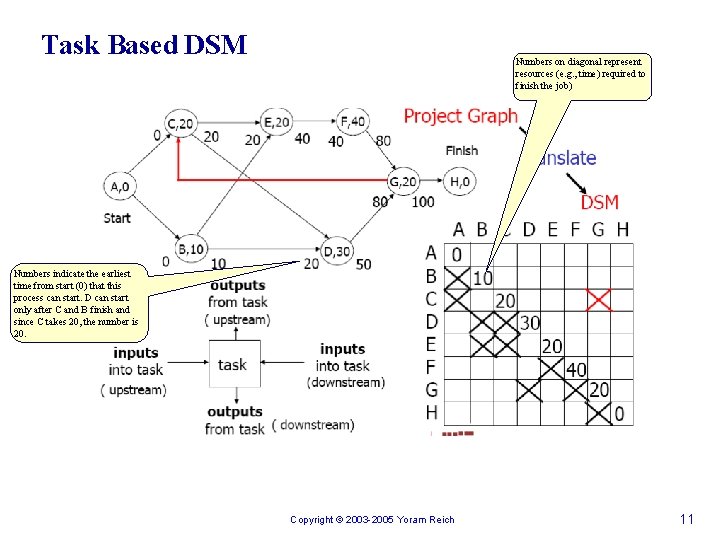
Task Based DSM Numbers on diagonal represent resources (e. g. , time) required to finish the job) Numbers indicate the earliest time from start (0) that this process can start. D can start only after C and B finish and since C takes 20, the number is 20. Copyright © 2003 -2005 Yoram Reich 11

Design Iteration Copyright © 2003 -2005 Yoram Reich 12

Observations Copyright © 2003 -2005 Yoram Reich 13

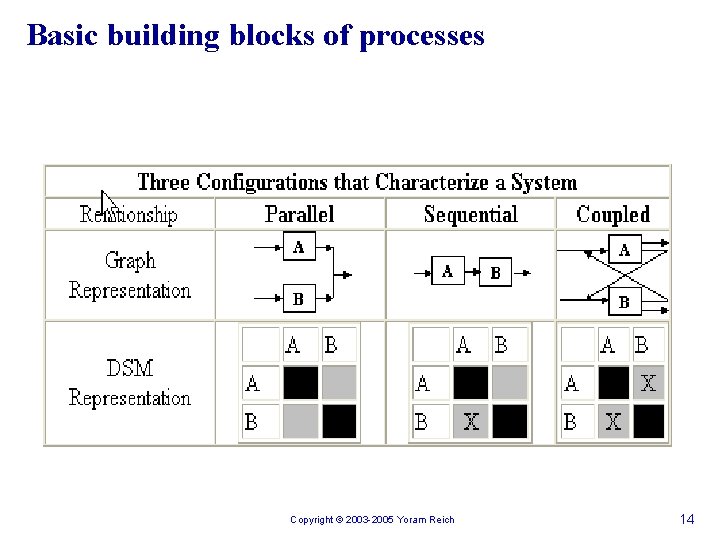
Basic building blocks of processes Copyright © 2003 -2005 Yoram Reich 14

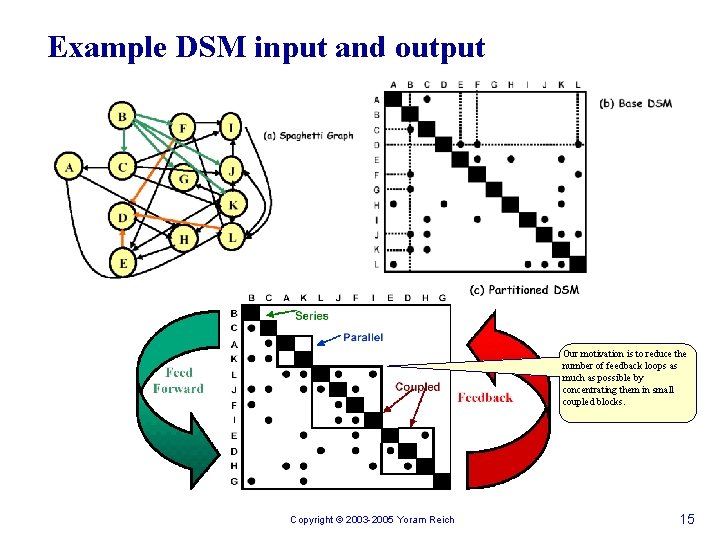
Example DSM input and output Our motivation is to reduce the number of feedback loops as much as possible by concentrating them in small coupled blocks. Copyright © 2003 -2005 Yoram Reich 15

DSM Partitioning The process of reordering the DSM rows and columns: n minimize the feedback marks and n moving them as close as possible to the diagonal (this form of the matrix is known as block triangular). Copyright © 2003 -2005 Yoram Reich 16

Partitioning algorithm n Simple algorithm (there are more) 1. Identify element(s) without input from other elements. (empty row). Place in top of the DSM § Remove the element (row, column) and Repeat 1 2. Identify element(s) without output to other elements. (empty column). Place in end top of the DSM § Remove the element (row, column) and Repeat 2 3. If no elements remain, then the matrix is partitioned; otherwise, the remaining elements contain circuits 4. Determine circuits (Powers of the Adjacency Matrix; Path search) § when a circuit found Collapse circuit – i. e. create one element and assign the inputs / outputs of circuit elements to this new element 5. Go to 1 When you go to 1, the “new” element might go to top (in step 1), bottom (in step 2), or stay. If another circuit is found and collapsed, then upon going to 1 again, they will be handles similarly or wait till another circuit is found. Copyright © 2003 -2005 Yoram Reich 17

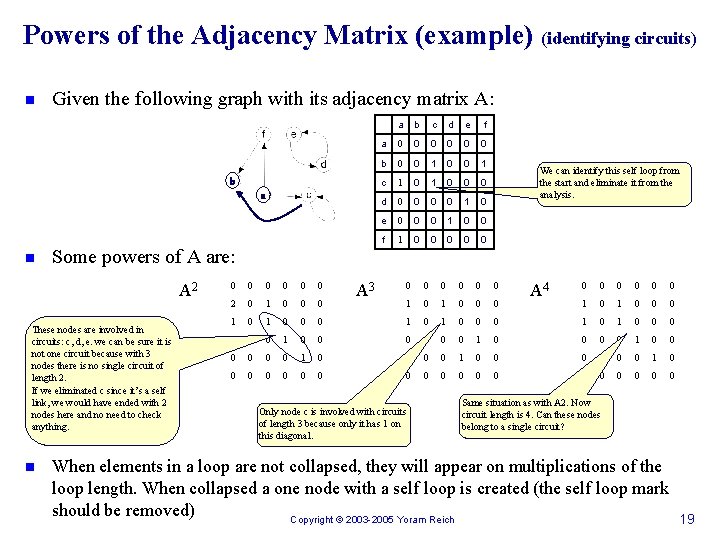
Powers of the Adjacency Matrix (identifying circuits) 1. 2. 3. 4. Replace a link marks with 1 All other with 0 (including the main diagonal) Raise the DSM to power p (starting at p = 2 ) If on the main diagonal there are markings, they belong to circuit(s) of size p. n 5. Stop Increase p until N (N –number of elements), go to 3 Notes: n on raising to power p there might be p elements indicating a circuit (loop) with size p, or K*p elements indicating K circuits of size p. n In the latter case a Path Searching or Breadth-First Search is required, but only between the indicated elements. n Self links could be easily identified from the original matrix and eliminated from the analysis. Copyright © 2003 -2005 Yoram Reich 18

Powers of the Adjacency Matrix (example) (identifying circuits) n Given the following graph with its adjacency matrix A: b a n a b c d e f a 0 0 0 b 0 0 1 c 1 0 0 0 d 0 0 1 0 e 0 0 0 1 0 0 f 1 0 0 0 We can identify this self loop from the start and eliminate it from the analysis. Some powers of A are: A 2 These nodes are involved in circuits: c, d, e. we can be sure it is not one circuit because with 3 nodes there is no single circuit of length 2. If we eliminated c since it’s a self link, we would have ended with 2 nodes here and no need to check anything. n 0 0 0 2 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 A 3 Only node c is involved with circuits of length 3 because only it has 1 on this diagonal. 0 0 0 1 0 0 0 1 0 0 0 0 A 4 Same situation as with A 2. Now circuit length is 4. Can these nodes belong to a single circuit? When elements in a loop are not collapsed, they will appear on multiplications of the loop length. When collapsed a one node with a self loop is created (the self loop mark should be removed) Copyright © 2003 -2005 Yoram Reich 19

Collapse a circuit (loop) n n n Sum all rows of the elements in the circuit to one representative row (any of the elements( Sum all columns of the elements in the circuit to a representative column (any of the elements( Delete all rows and columns of the other elements in the circuit Each number, which is greater than 1, turn to 1 Replace the number on the diagonal to zero Copyright © 2003 -2005 Yoram Reich 20

Path Searching (identifying circuits) n n n Path search is done on the DSM (not on DSM^k) Starting from any element, follow the dependencies (on row) until at some point an element is reached again. Stop The result circuit (loop) is from the first appearance of the element to its second appearance (not the first element which was checked) Notes n Path searching can be used on its own starting from any element (after completing steps 1 2). Or, can be complementary item to Powers of Matrix n In the general case minimal circuit (loops) are not guarantied n Searching only within the results of Power of matrix (at each step) does result in minimal circuits. Copyright © 2003 -2005 Yoram Reich 21

Breadth-First Search (BFS) (identifying circuits) n This is a graph algorithm since DSM represents a directed graph, it can be used for finding DSM circuits (loops) as well Algorithm (On the original DSM) 1. 2. 3. 4. Starting from any element, add it to a buffer (or queue, i. e. first in first out) If current element (first in the buffer) is reached again (current element already in history list) there is a loop, Stop. For current element (first in the buffer) go to all the next elements (on the row) add them to the buffer, then remove the current element from the beginning of the buffer and keep in history list. Go to 2 Copyright © 2003 -2005 Yoram Reich 22

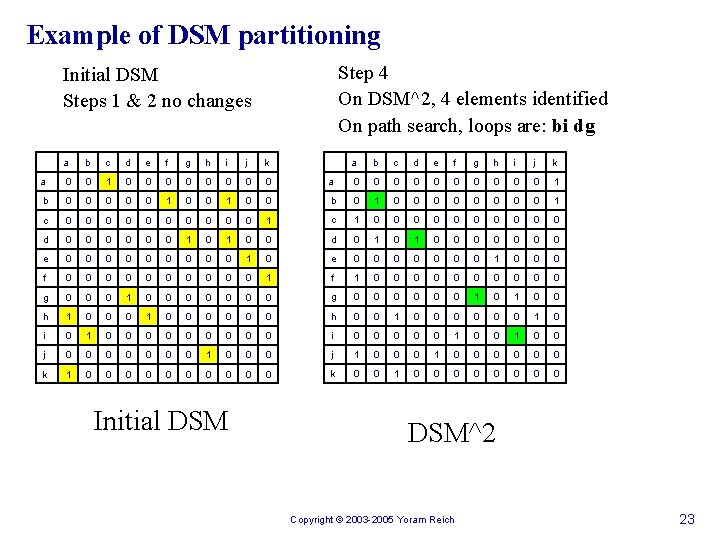
Example of DSM partitioning Step 4 On DSM^2, 4 elements identified On path search, loops are: bi dg Initial DSM Steps 1 & 2 no changes a b c d e f g h i j k a 0 0 0 0 0 1 0 b 0 1 0 0 0 0 1 0 1 c 1 0 0 0 0 0 1 0 0 d 0 1 0 0 0 0 0 1 0 e 0 0 0 0 1 f 1 0 0 0 0 g 0 0 0 1 0 0 0 h 0 0 1 0 0 0 0 i 0 0 0 1 0 0 0 j 1 0 0 0 0 0 k 0 0 1 0 0 0 0 a b c d e f g h i j k a 0 0 1 0 0 0 0 b 0 0 0 1 0 c 0 0 0 0 0 d 0 0 0 1 0 e 0 0 0 0 f 0 0 0 g 0 0 0 1 0 h 1 0 0 0 i 0 1 0 j 0 0 k 1 0 Initial DSM^2 Copyright © 2003 -2005 Yoram Reich 23

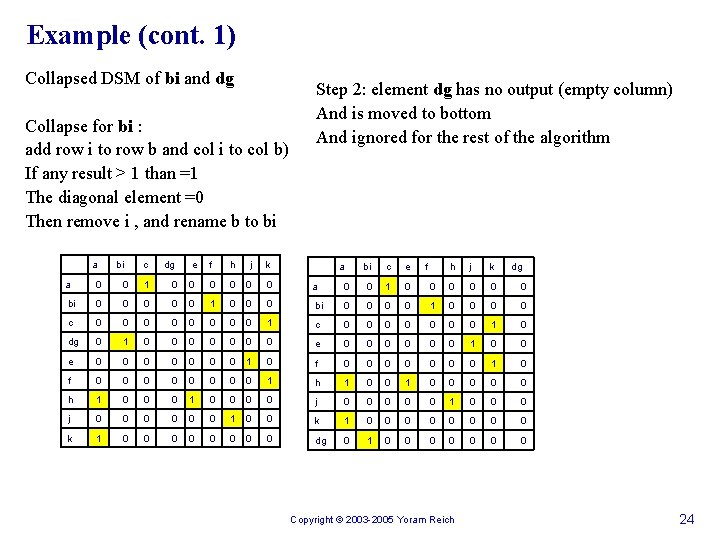
Example (cont. 1) Collapsed DSM of bi and dg Collapse for bi : add row i to row b and col i to col b) If any result > 1 than =1 The diagonal element =0 Then remove i , and rename b to bi a bi c dg e f h j k Step 2: element dg has no output (empty column) And is moved to bottom And ignored for the rest of the algorithm a bi c e f h j k dg a 0 0 1 0 0 0 bi 0 0 0 1 0 0 0 bi 0 0 1 0 0 c 0 0 0 0 1 0 dg 0 1 0 0 0 0 e 0 0 0 1 0 0 e 0 0 0 0 1 0 f 0 0 0 0 1 h 1 0 0 0 0 0 h 1 0 0 0 0 j 0 0 0 1 0 0 k 1 0 0 0 0 dg 0 1 0 0 0 0 Copyright © 2003 -2005 Yoram Reich 24

Example (cont. 2) The new DSM^2 – no diagonal ‘ 1’ DSM^3 reveals 2 loops of 3 elements On path search, loops are: akc and ehj a b i c e f h j k d g a 1 0 0 0 0 bi 1 0 0 0 0 c 0 0 1 0 0 0 e 1 0 0 0 0 0 f 0 0 1 0 0 0 h 0 0 0 1 0 j 0 0 1 0 0 k 0 0 0 0 1 0 dg 0 0 0 0 1 0 Collapsed DSM of akc and ehj Step 1 akc – to top Step 1 f – to top Step 2 bi, ehi – to bottom That is the algorithm end f d g a k c 0 0 0 akc 0 0 0 0 1 0 f 1 0 0 0 0 bi 0 1 0 0 0 f 1 0 0 eh j 1 0 0 dg 0 1 0 0 0 dg 0 0 1 0 0 a kc b i e h j akc 0 0 bi 0 eh j Copyright © 2003 -2005 Yoram Reich f b i e h j d g 25

Example (Cont 3) Final result After expansion of collapsed elements a k c f b i e h j d g a 0 0 1 0 0 0 0 k 1 0 0 0 0 0 c 0 1 0 0 0 0 0 f 0 1 0 0 0 0 0 b 0 0 0 1 0 0 0 i 0 0 1 0 0 0 e 0 0 0 0 1 0 0 h 1 0 0 0 1 0 0 j 0 0 0 0 1 0 0 0 d 0 0 0 1 g 0 0 0 0 0 1 0 Compare this DSM to the initial DSM How will the result change if a link ‘e’ to ‘a’ is added ? How will the result change if a link ‘d’ to ‘b’ is added? Copyright © 2003 -2005 Yoram Reich 26

Optimal partitioning n Complex optimization problem: u u u n Solutions are discrete (optimization methods based on derivatives are not applicable) Multiple local minima Large solution space n!*2^(n-1) N! is the number of ways to order the n tasks and 2(n-1) is the number of ways to create subsets from each such ordering. Search algorithms are typically used u Main concept 1. 2. 3. Create potential solution(s) Choose best solution(s) to continue with , according to a cost function Until an exit decision criteria, Go to 1 Copyright © 2003 -2005 Yoram Reich 27

Optimal partitioning (cont. ) n Algorithm concept examples: F Genetic Algorithms (GA) • Create gene population (solution) • Choose best genes • Create new generation out of previous one F Simulated Annealing (SA) • allow “jumps” to a solution which is worse than current as a new search start, • The probability of such an occasion, decreases with search ”time”, as search continues. n Cost function examples for partitioning u u Distance from diagonal (being close to main diagonal) Distance from lower left point Copyright © 2003 -2005 Yoram Reich 28

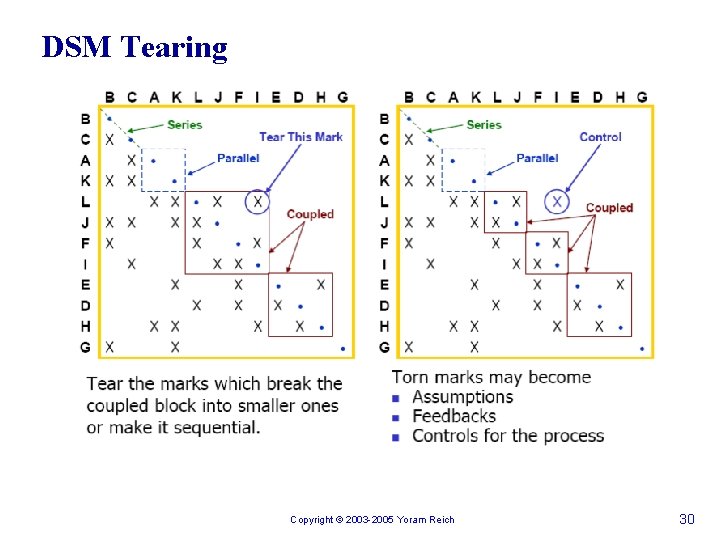
DSM Tearing n n Removing feedback marks that result in lower triangular matrix. The marks that we remove from the matrix are called "tears". Means: identifying the set of assumptions to be made in order to start design process iterations. u n n Having made these assumptions, no additional estimates need to be made. No optimal method exist for tearing Recommendations: u u u Minimal number of tears (reduces estimates) Seek small diagonal blocks, (fewer iterations) Choose easiest activity estimates Copyright © 2003 -2005 Yoram Reich 29

DSM Tearing Copyright © 2003 -2005 Yoram Reich 30

DSM Banding n n Addition of alternating light/dark bands to show independent activities (ignoring feedback) The collection of bands or levels within a DSM constitute the critical path of the system/project. One element/activity within each band is the critical/bottleneck activity. Thus, fewer bands are preferred since they improve the concurrency of the system/project Copyright © 2003 -2005 Yoram Reich 31

DSM Banding n Identification of serial/parallel activities u u u Do not consider feedback links Example 4 & 5 are independent (parallel) Also 7 & 8, 9 & 10 Copyright © 2003 -2005 Yoram Reich 32

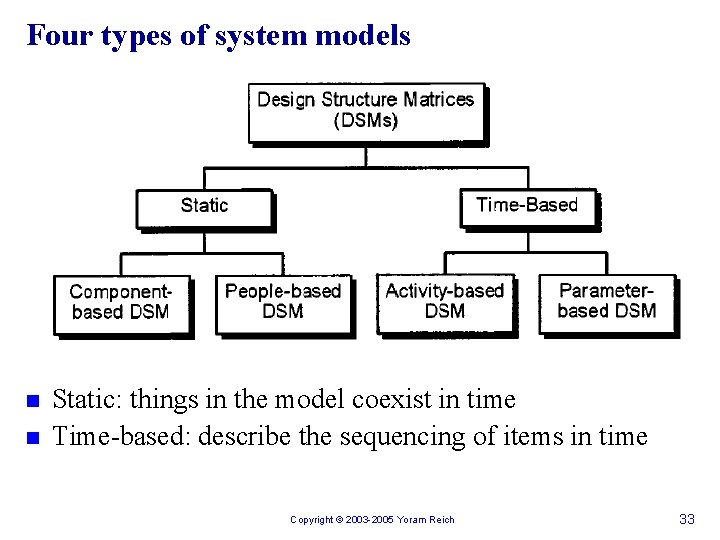
Four types of system models n n Static: things in the model coexist in time Time-based: describe the sequencing of items in time Copyright © 2003 -2005 Yoram Reich 33

Four types of system models n Static: u Component-based Relationships between multiple components of the project F System architecting F u People-based Relationships between people/teams involved in the project F Organizational/project design, team integration F n Time-based: u Activity-based Relationships between output and input of activities F Project scheduling F u Parameter-based Influences between decisions on the values of parameters F Low level activity sequencing F Copyright © 2003 -2005 Yoram Reich 34

Four types of system models n Analysis method u Static F clustering u Time-based F Partitioning/sequencing Copyright © 2003 -2005 Yoram Reich 35

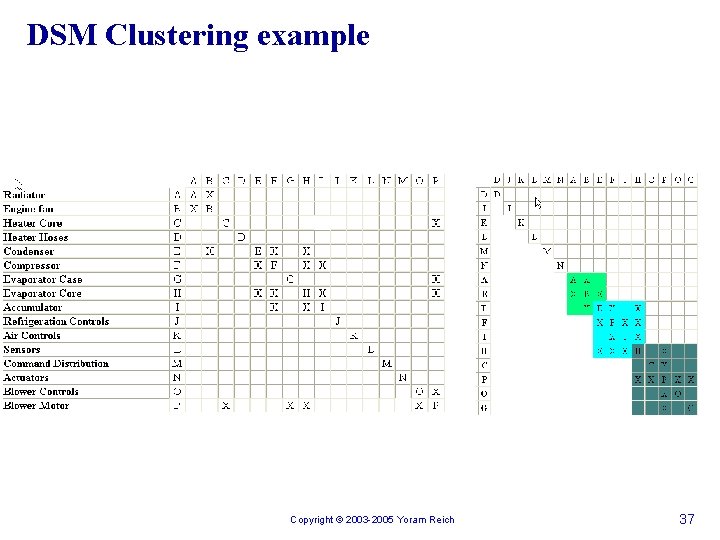
DSM Clustering n n Goal: finding subsets of DSM elements (i. e. clusters or modules) that are mutually exclusive or minimally interacting subsets Used when the DSM elements represent design components or teams within a development project Copyright © 2003 -2005 Yoram Reich 36

DSM Clustering example Copyright © 2003 -2005 Yoram Reich 37

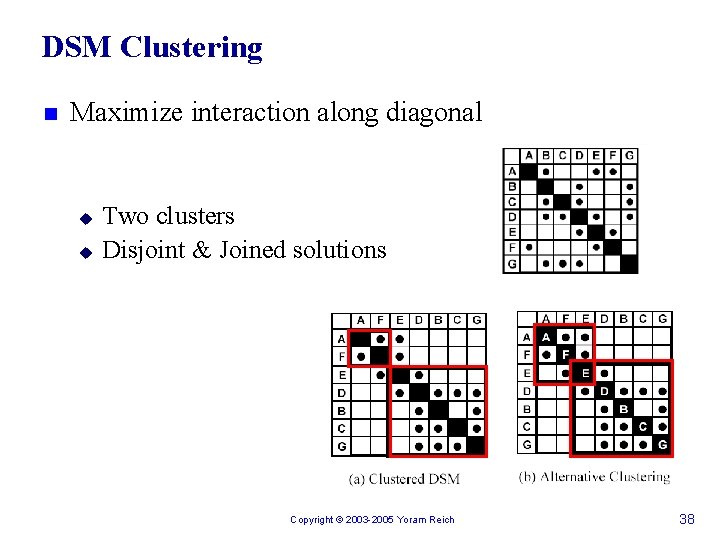
DSM Clustering n Maximize interaction along diagonal u u Two clusters Disjoint & Joined solutions Copyright © 2003 -2005 Yoram Reich 38

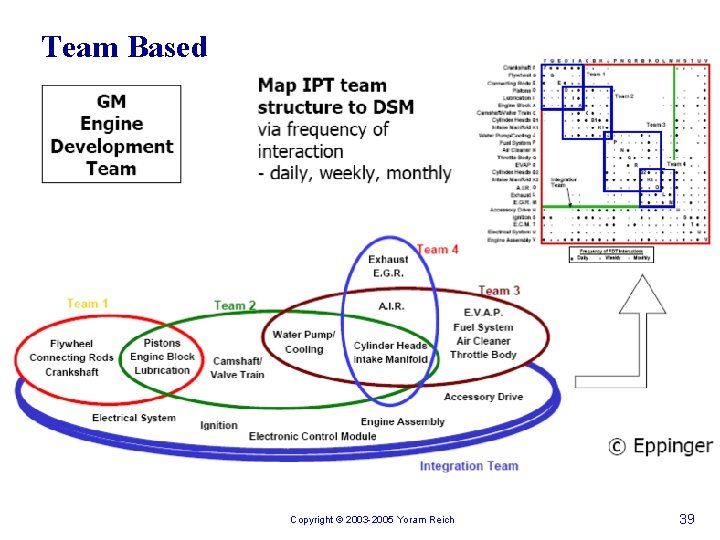
Team Based Copyright © 2003 -2005 Yoram Reich 39

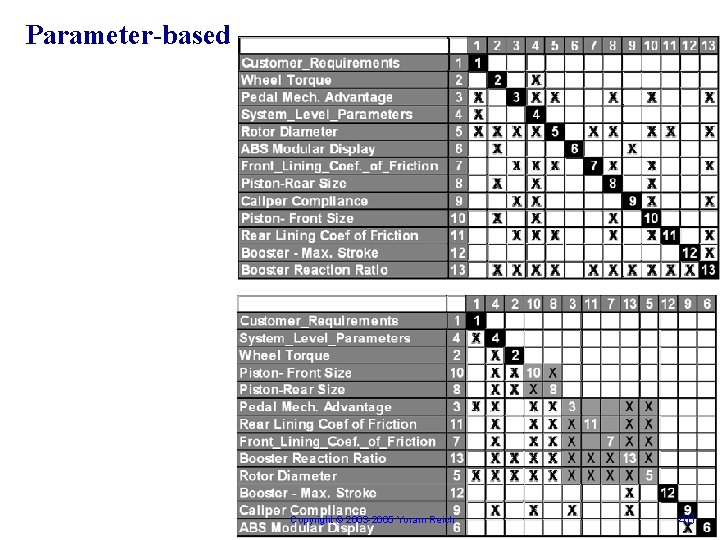
Parameter-based Copyright © 2003 -2005 Yoram Reich 40

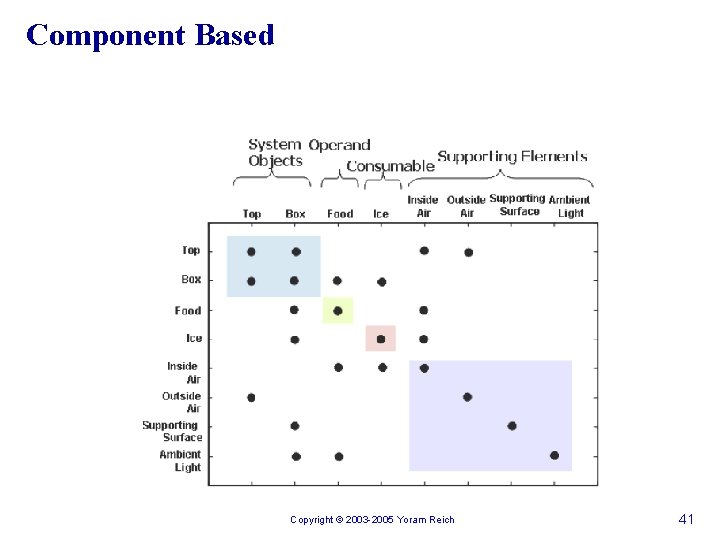
Component Based Copyright © 2003 -2005 Yoram Reich 41

Building a DSM n n n Interview engineers and managers Determine list of tasks or parameters Ask about inputs, outputs, strengths of interaction, etc Enter marks in matrix (we have Excel macros to help ( Check with engineers and managers to verify/comment on DSM Copyright © 2003 -2005 Yoram Reich 42

Bibliography n n n The DSM site http: //www. dsmweb. org/ Tutorial : http: //www. dsmweb. org/Tutorial/tutorial. htm Other presentations www. gerc. eng. ufl. edu/Faculty%20 pages/ Pfister/Fall 05/Class 14. ppt Copyright © 2003 -2005 Yoram Reich 43