DSHEP 2017 Deep Learning and Structures Kyunghyun Cho

DS@HEP 2017 Deep Learning and Structures Kyunghyun Cho Courant Institute (Computer Science) http: //cs. nyu. edu/ Center for Data Science http: //cds. nyu. edu/ New York University

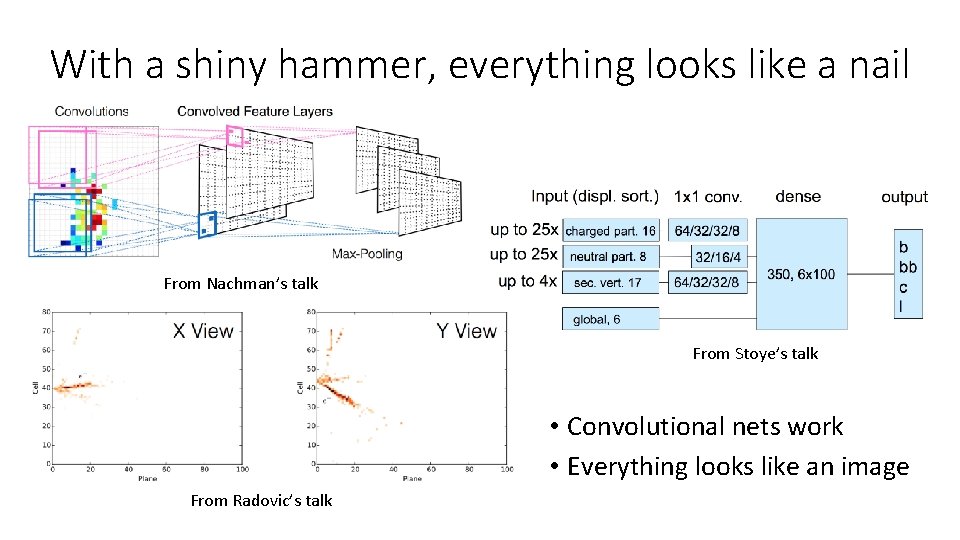
With a shiny hammer, everything looks like a nail From Nachman’s talk From Stoye’s talk • Convolutional nets work • Everything looks like an image From Radovic’s talk

Fully connected network, recurrent network, convolutional network to recursive network From mid-80’s to 2016

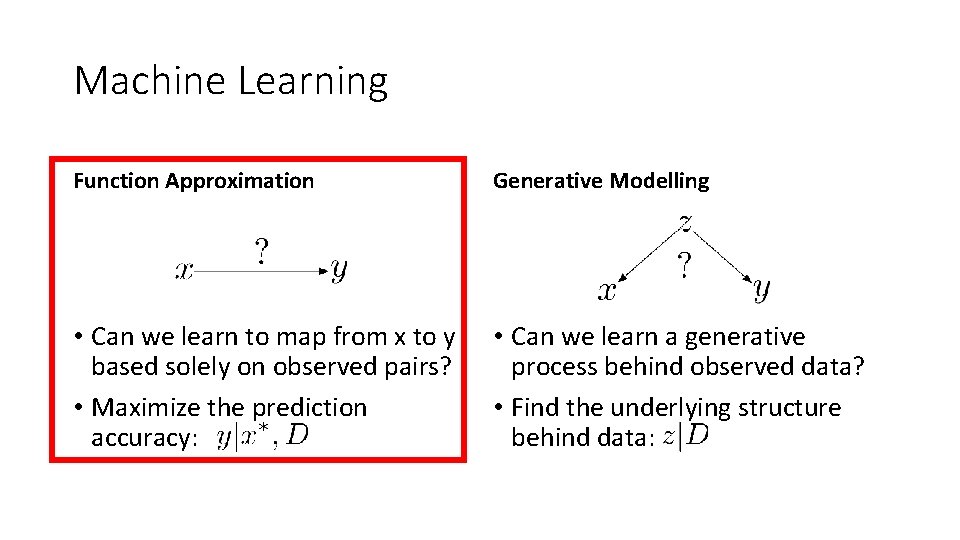
Machine Learning Function Approximation Generative Modelling • Can we learn to map from x to y based solely on observed pairs? • Maximize the prediction accuracy: • Can we learn a generative process behind observed data? • Find the underlying structure behind data:

Multilayer Perceptron • Function approximation: • Potentially nonlinear mapping from x to y • Multi-layer perceptron • Nonlinear transformation layer • Stack of them allows us to learn an arbitrary, highly nonlinear mapping • and are fixed-dimensional real-valued vectors

Multilayer Perceptron - Learning • Learning by optimization • Cost function: • Backpropagation • Chain rule of derivative for efficient computation • Reverse mode automatic differentiation • Implemented for many frameworks: Stan, autograd, Theano, TF, Py. Torch, … • Stochastic gradient descent optimization

Multilayer Perceptron - Regularization • Large # of parameters (tens or hundreds of millions of weight values) • Heavy overfitting: MLP easily remembers every training example • Dropout • Set each dimension of h to 0 randomly • Often with a probability p=0. 5 • Multiply each dimension with p after training • Weight decay • Not used too often these days • Ensemble of multilayer perceptrons • Very effective when the output is a distribution, such as a classifier •

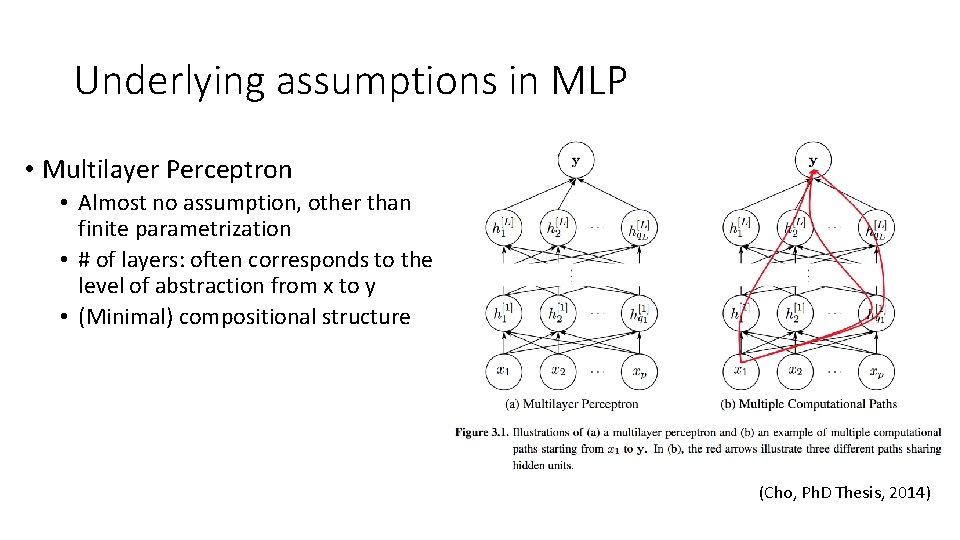
Underlying assumptions in MLP • Multilayer Perceptron • Almost no assumption, other than finite parametrization • # of layers: often corresponds to the level of abstraction from x to y • (Minimal) compositional structure (Cho, Ph. D Thesis, 2014)

Multilayer Perceptron – In practice Building MLP Training MLP with SGD

Recurrent nets for sequence input • Sequence input: • Vector output: • Necessary to compress/summarize the input sequence x • MLP with shared weights • Most of techniques from MLP learning all apply: SGD, dropout, … • The length of each training input may vary

Recurrent nets for sequence input • Sequence input: , Vector output: • Most of techniques from MLP learning all apply: SGD, dropout, … • But, we couldn’t train them in 90’s [Bengio et al. , 1994; Hochreiter, 1992] • Why?

Recurrent nets for sequence input • Sequence input: , Vector output: • But, we couldn’t train them in 90’s [Bengio et al. , 1994; Hochreiter, 1992] • Why? • Learning a recurrent net = detecting long-term dependencies • The repeated product of a squared matrix multiplied with a vector either • Vanishes, if the largest eigenvalue < 1 • Explodes, if the largest eigenvalue > 1

Recurrent nets for sequence input • Sequence input: , Vector output: • But, we couldn’t train them in 90’s [Bengio et al. , 1994; Hochreiter, 1992] • Addressing the issue of exploding gradient: gradient clipping [Pascanu et al. , 2011] • Useful for a deep MLP as well • Related to trust region methods

Recurrent nets for sequence input • Sequence input: , Vector output: • But, we couldn’t train them in 90’s [Bengio et al. , 1994; Hochreiter, 1992] • Vanishing gradient happened! What caused it? 1. The network’s not configured correctly 2. There’s no long-term dependency in data • We cannot tell…

Recurrent nets for sequence input • Sequence input: , Vector output: • Instead, let us make a better recurrent activation function 1. Build a shortcut connection across time, if necessary. 2. Disconnect a connection, if unnecessary. • These decision are made adaptively: 1. Update gate: 2. Reset gate: [Cho et al. , 2014; Hochreiter & Schmidhuber, 1999]

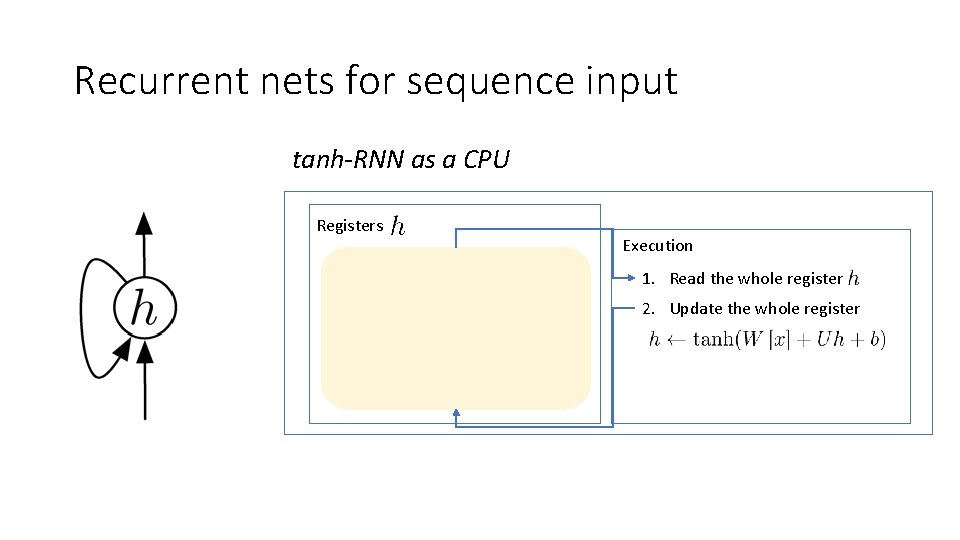
Recurrent nets for sequence input tanh-RNN as a CPU Registers Execution 1. Read the whole register 2. Update the whole register

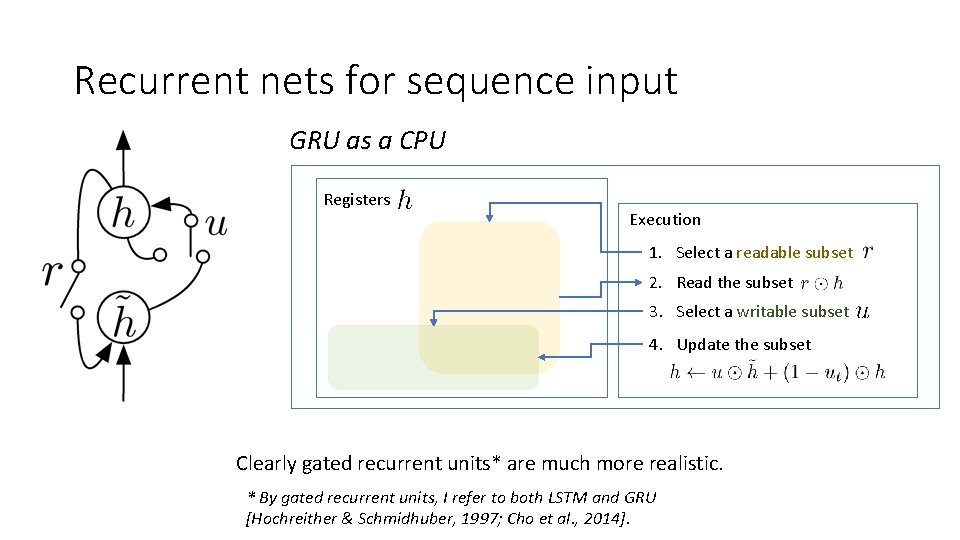
Recurrent nets for sequence input GRU as a CPU Registers Execution 1. Select a readable subset 2. Read the subset 3. Select a writable subset 4. Update the subset Clearly gated recurrent units* are much more realistic. * By gated recurrent units, I refer to both LSTM and GRU [Hochreither & Schmidhuber, 1997; Cho et al. , 2014].

Recurrent nets for sequence input • In practice, GRU or LSTM RNN’s are so much easier to train and work well with a wider range of hyperparameters

Recurrent Network – In practice Building MLP No change in training Building RNN

Underlying assumptions in RNN • Recurrent Network • An input sequence x is best summarized reading it in a given order. • Immediate neighboring symbols are likely more important. • Reasonable when reading a natural language sentence • Think of listening to a speaker: words arrive in a sequence

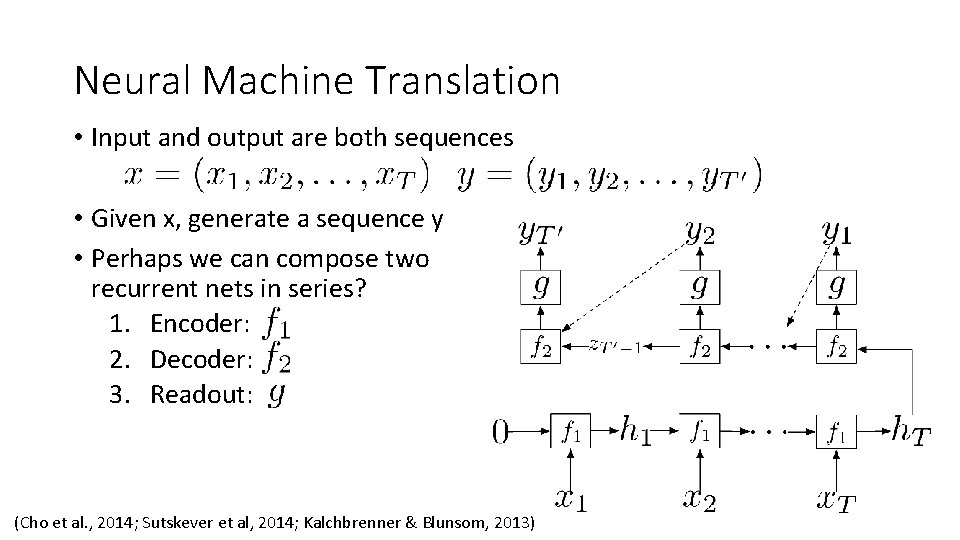
Neural Machine Translation • Input and output are both sequences • Given x, generate a sequence y • Perhaps we can compose two recurrent nets in series? 1. Encoder: 2. Decoder: 3. Readout: (Cho et al. , 2014; Sutskever et al, 2014; Kalchbrenner & Blunsom, 2013)

Neural Machine Translation • Straightforward idea: 1. Let the encoder summarize the source sentence 2. the decoder updates its own state/memory 3. outputs the distribution over the next target symbol 4. Repeat 2 -3 • Surprisingly successful! • State-of-the-art method for En-Fr in 2014 • [Sutskever et al. , 2014 NIPS]

Attention-based Neural Machine Translation • What do we know about translation? • A sentence must be considered as a whole rather than pieces. • A source sentence can be looked into more than once • For each target symbol, different parts of a source sentence matters • Can we encode these domain knowledge into a recurrent network?

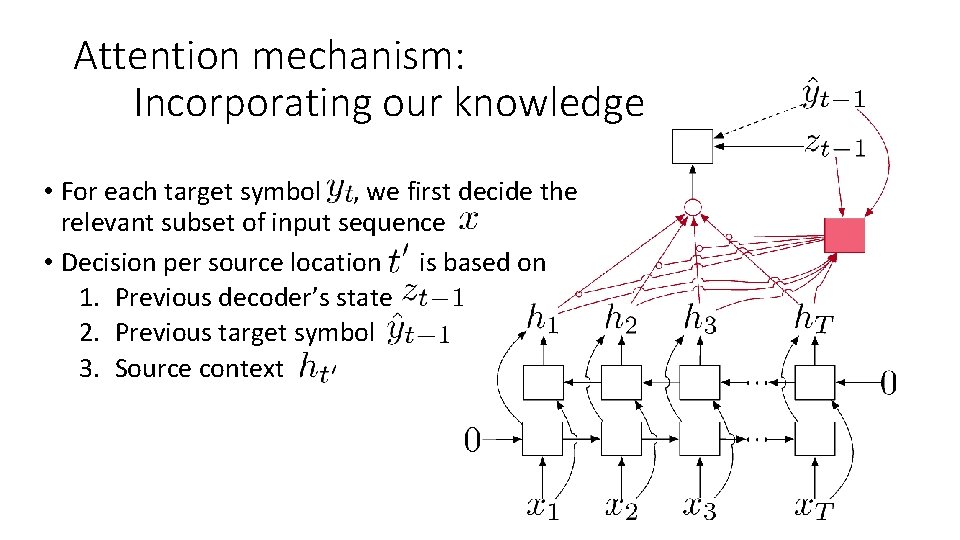
Attention mechanism: Incorporating our knowledge • For each target symbol , we first decide the relevant subset of input sequence • Decision per source location is based on 1. Previous decoder’s state 2. Previous target symbol 3. Source context

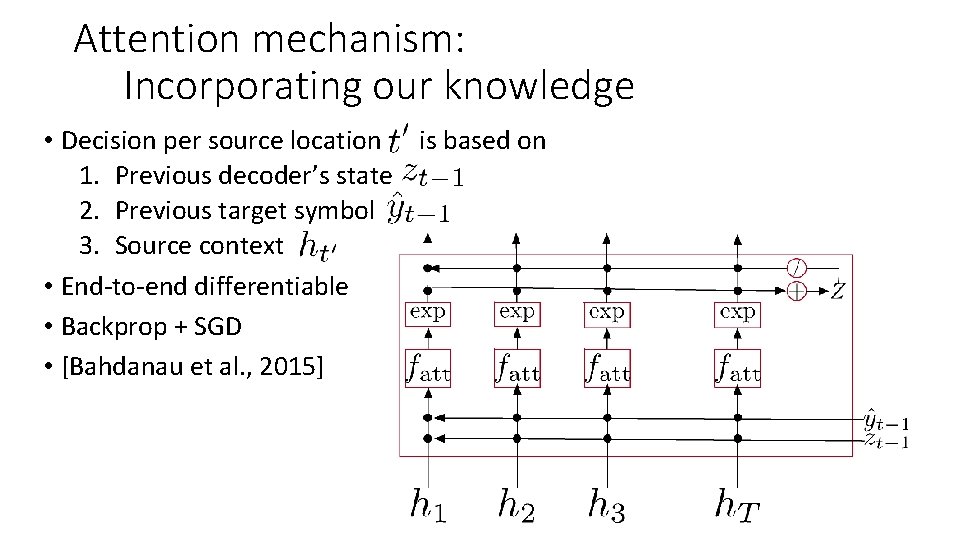
Attention mechanism: Incorporating our knowledge • Decision per source location is based on 1. Previous decoder’s state 2. Previous target symbol 3. Source context • End-to-end differentiable • Backprop + SGD • [Bahdanau et al. , 2015]

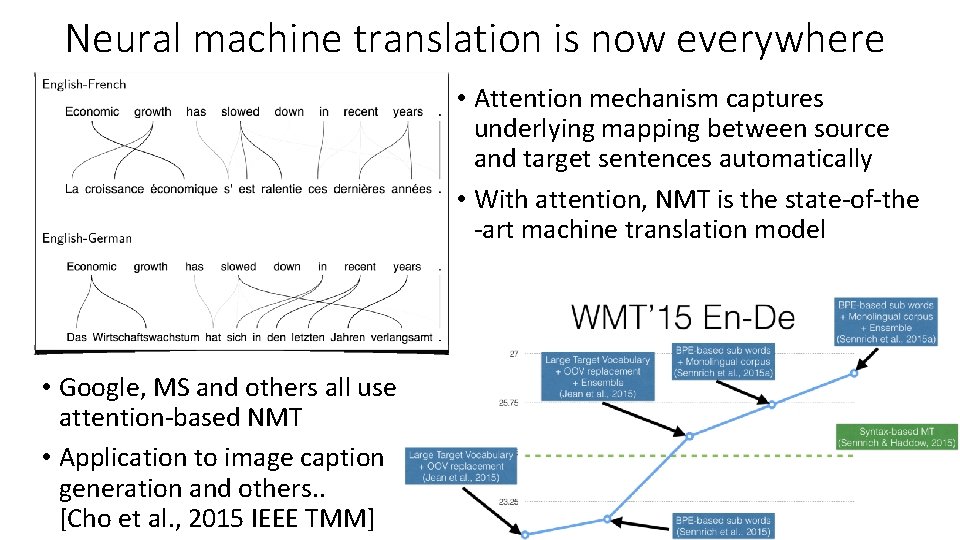
Neural machine translation is now everywhere • Attention mechanism captures underlying mapping between source and target sentences automatically • With attention, NMT is the state-of-the -art machine translation model • Google, MS and others all use attention-based NMT • Application to image caption generation and others. . [Cho et al. , 2015 IEEE TMM]

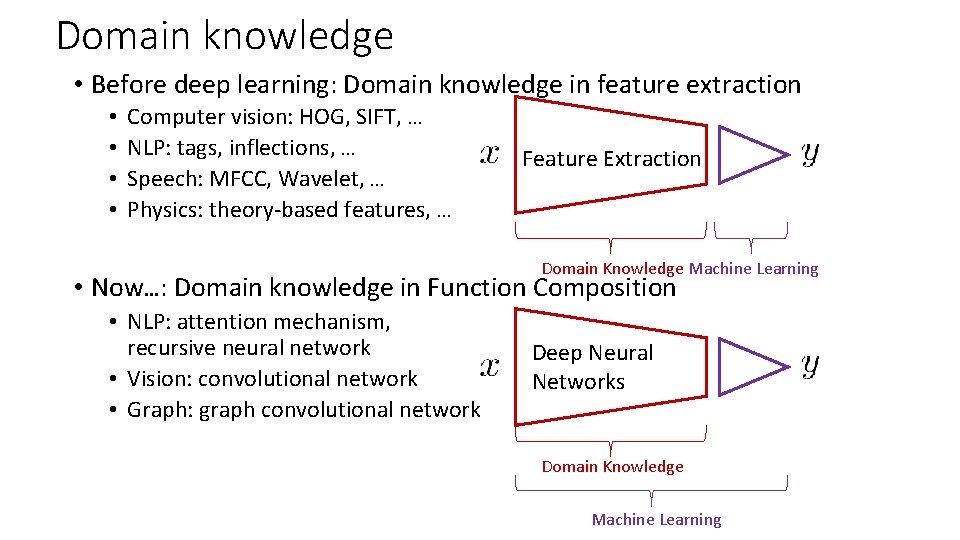
Domain knowledge • Before deep learning: Domain knowledge in feature extraction • • Computer vision: HOG, SIFT, … NLP: tags, inflections, … Speech: MFCC, Wavelet, … Physics: theory-based features, … Feature Extraction Domain Knowledge Machine Learning • Now…: Domain knowledge in Function Composition • NLP: attention mechanism, recursive neural network • Vision: convolutional network • Graph: graph convolutional network Deep Neural Networks Domain Knowledge Machine Learning

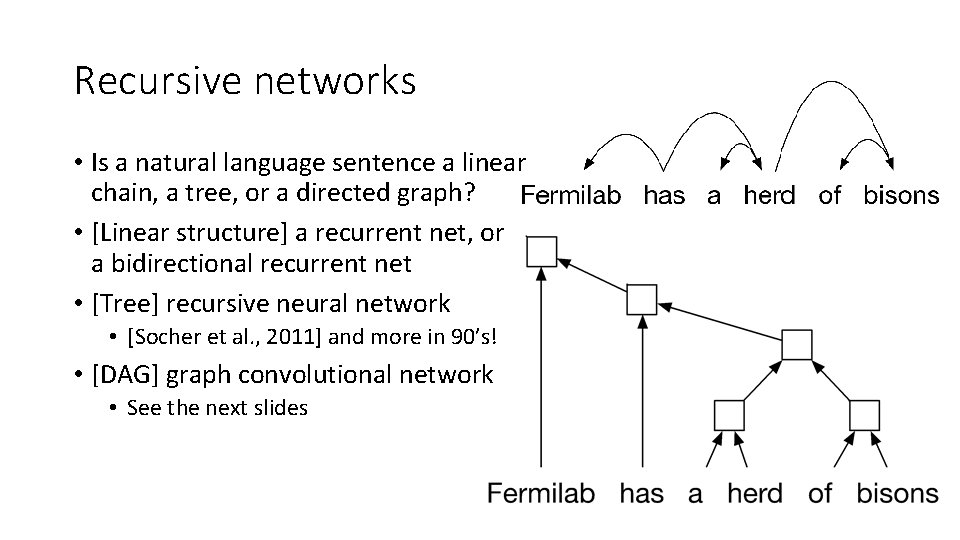
Recursive networks • Is a natural language sentence a linear chain, a tree, or a directed graph? • [Linear structure] a recurrent net, or a bidirectional recurrent net • [Tree] recursive neural network • [Socher et al. , 2011] and more in 90’s! • [DAG] graph convolutional network • See the next slides

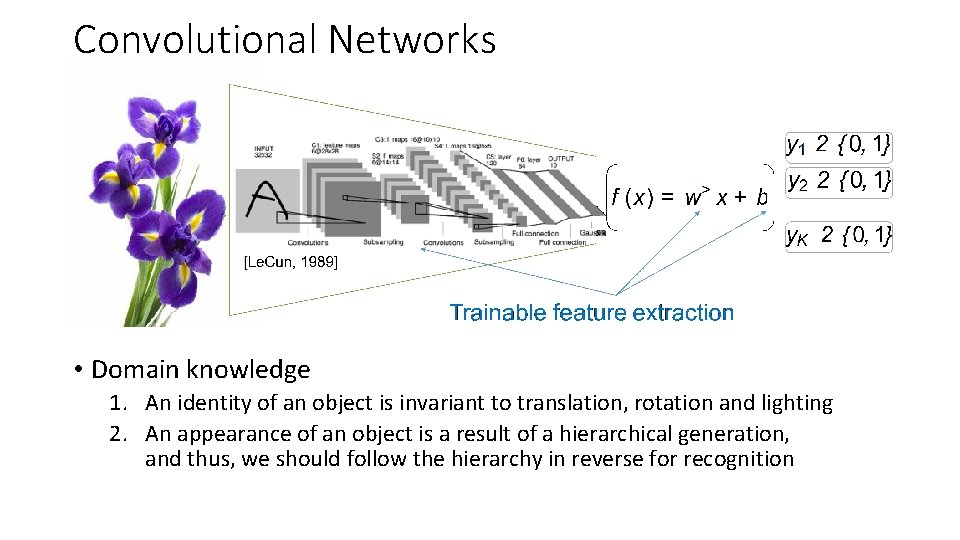
Convolutional Networks • Domain knowledge 1. An identity of an object is invariant to translation, rotation and lighting 2. An appearance of an object is a result of a hierarchical generation, and thus, we should follow the hierarchy in reverse for recognition

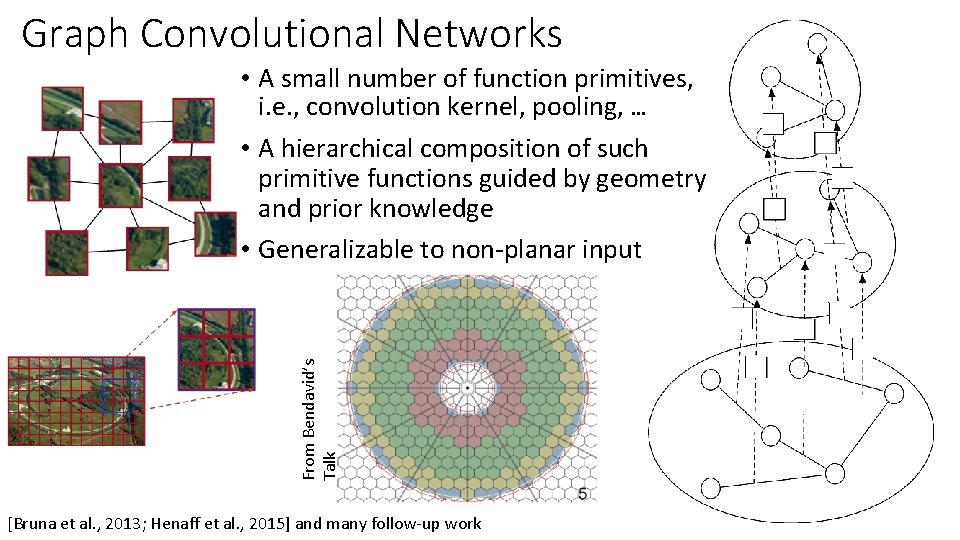
Graph Convolutional Networks From Bendavid’s Talk • A small number of function primitives, i. e. , convolution kernel, pooling, … • A hierarchical composition of such primitive functions guided by geometry and prior knowledge • Generalizable to non-planar input [Bruna et al. , 2013; Henaff et al. , 2015] and many follow-up work

Neural net approximation of a partially-known compositional function Balancing prior knowledge and trainable function approximation

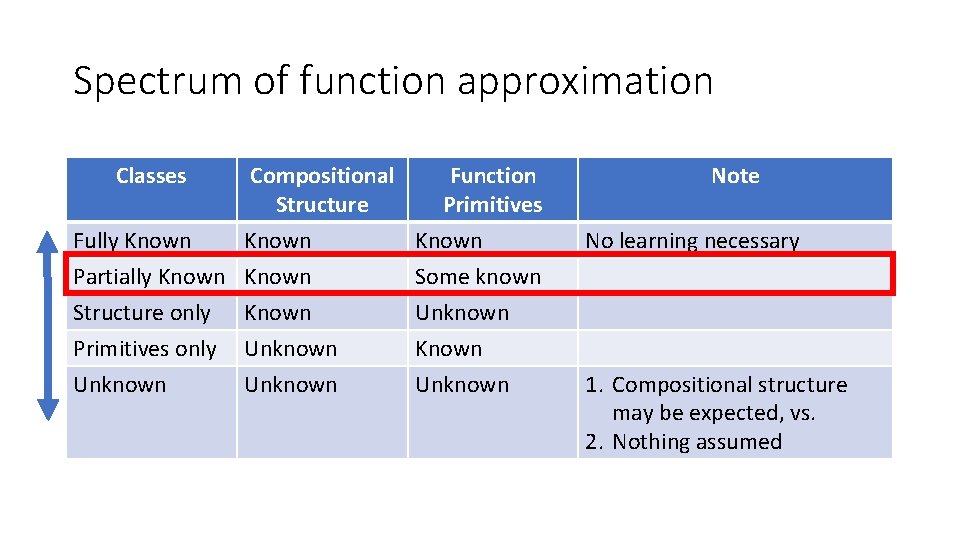
Spectrum of function approximation Classes Compositional Structure Function Primitives Fully Known Partially Known Some known Structure only Primitives only Unknown Known Unknown Note No learning necessary 1. Compositional structure may be expected, vs. 2. Nothing assumed

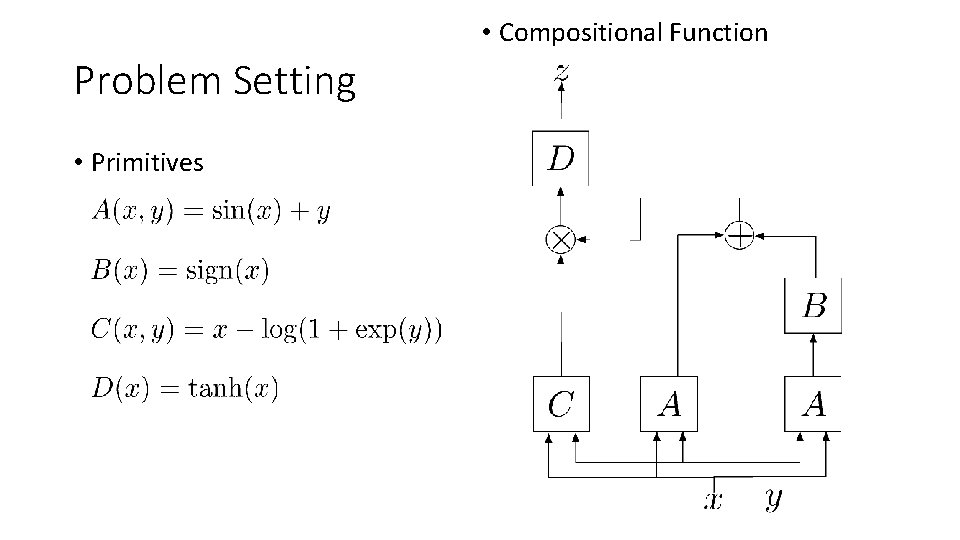
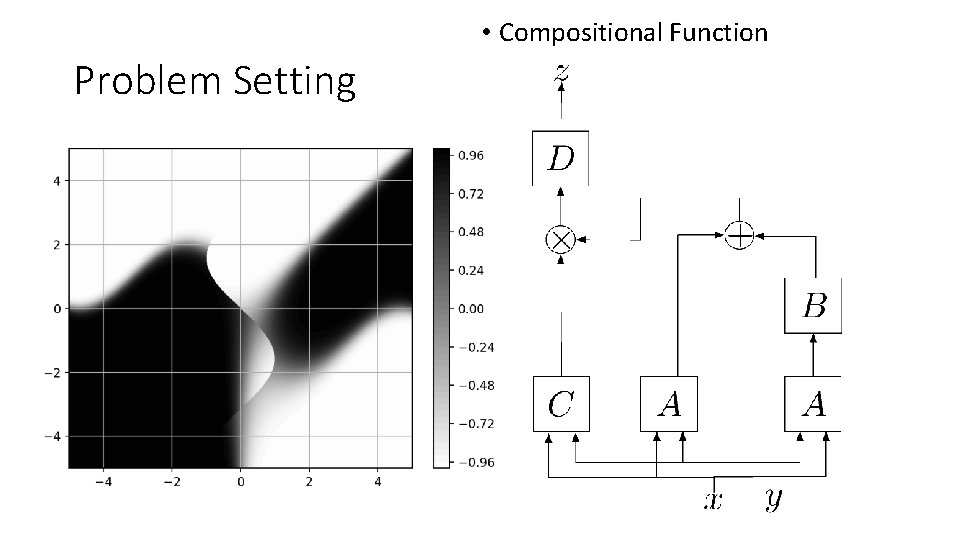
• Compositional Function Problem Setting • Primitives

• Compositional Function Problem Setting

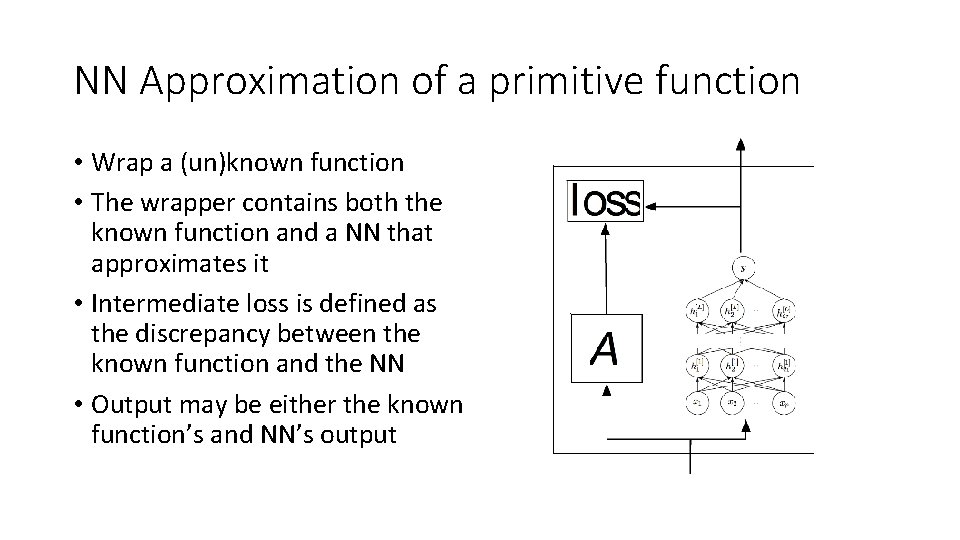
NN Approximation of a primitive function • Wrap a (un)known function • The wrapper contains both the known function and a NN that approximates it • Intermediate loss is defined as the discrepancy between the known function and the NN • Output may be either the known function’s and NN’s output

NN Approximation of a primitive function • Simple wrapper written in Py. Torch • Write a python function • Input: a list of numpy. ndarray • Ouput: numpy. ndarray • Wrap it with Function • Specify input and output dims • Pass a known function, if exists

NN Approximation of a primitive function • Write a compositional function • Supports most of python operators • Supports any control flow (for, if, while, …) • Enabled by dynamic computation of Py. Torch

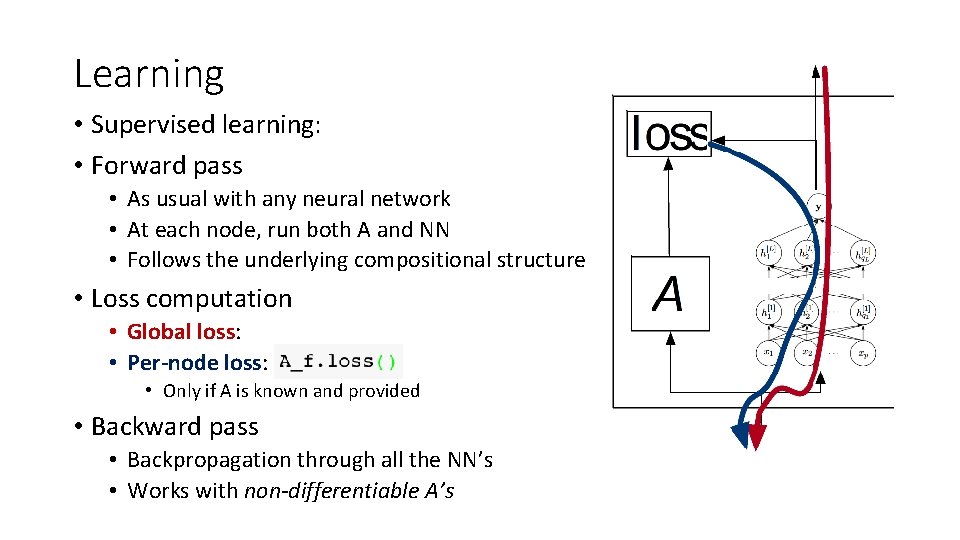
Learning • Supervised learning: • Forward pass • As usual with any neural network • At each node, run both A and NN • Follows the underlying compositional structure • Loss computation • Global loss: • Per-node loss: • Only if A is known and provided • Backward pass • Backpropagation through all the NN’s • Works with non-differentiable A’s

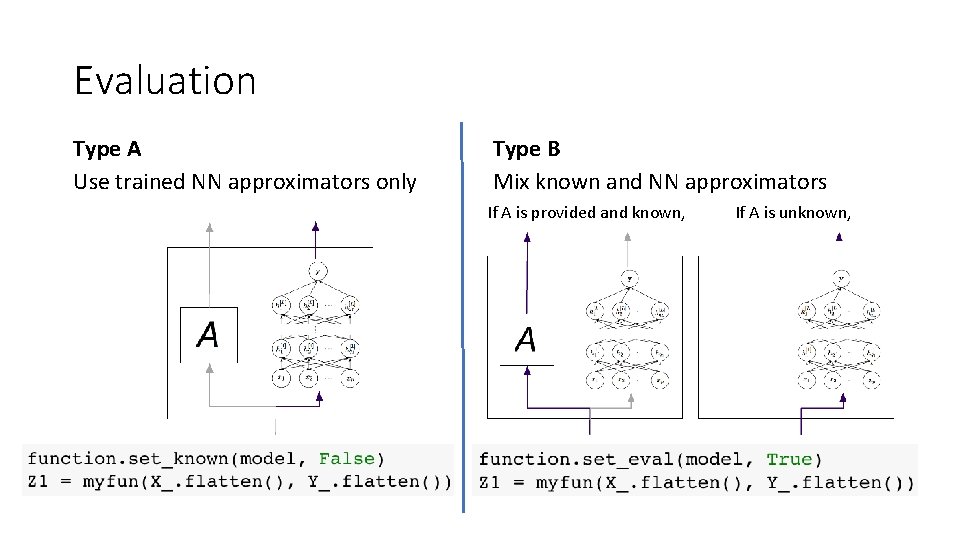
Evaluation Type A Use trained NN approximators only Type B Mix known and NN approximators If A is provided and known, If A is unknown,

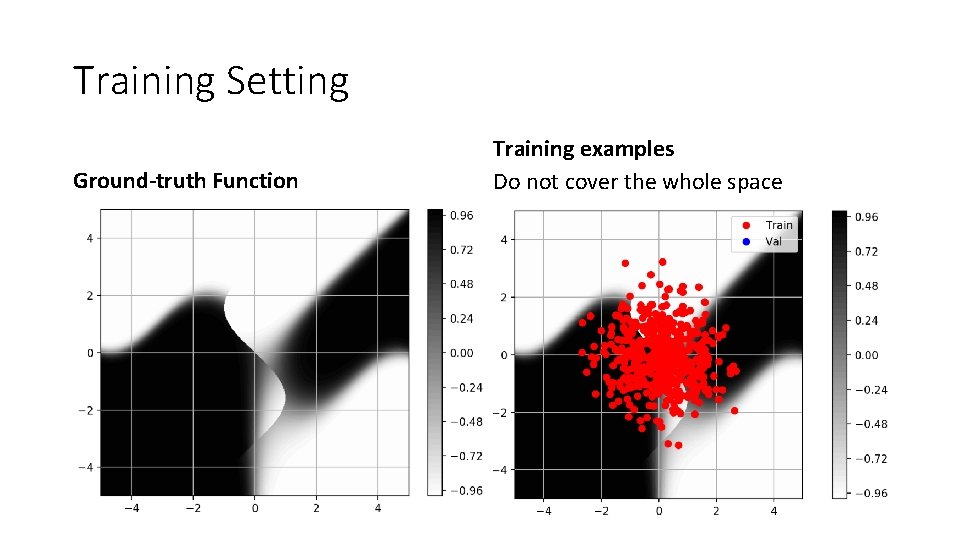
Training Setting Ground-truth Function Training examples Do not cover the whole space

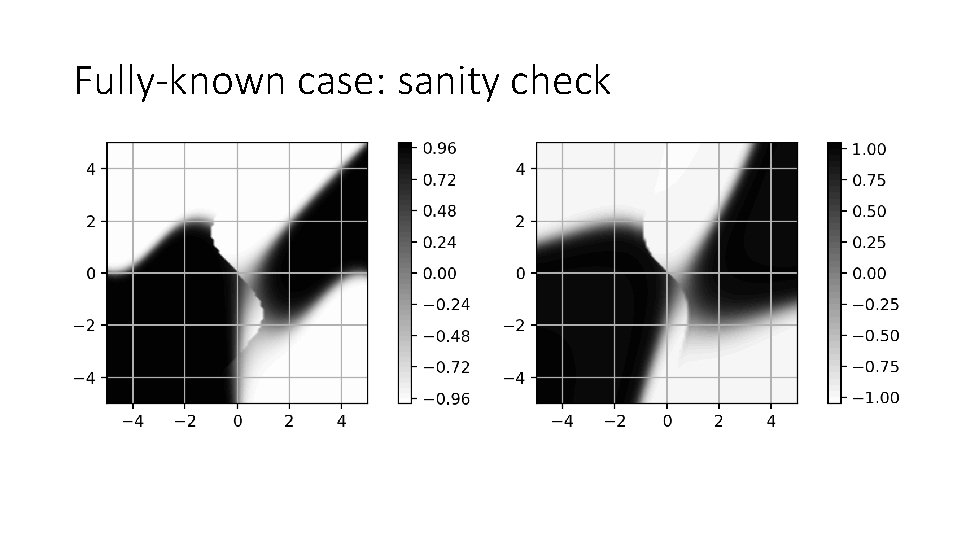
Fully-known case: sanity check

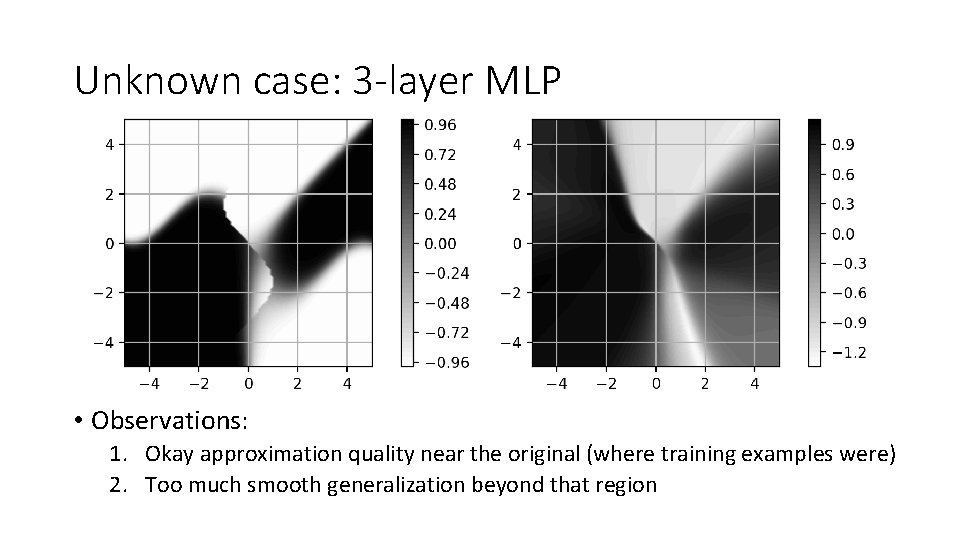
Unknown case: 3 -layer MLP • Observations: 1. Okay approximation quality near the original (where training examples were) 2. Too much smooth generalization beyond that region

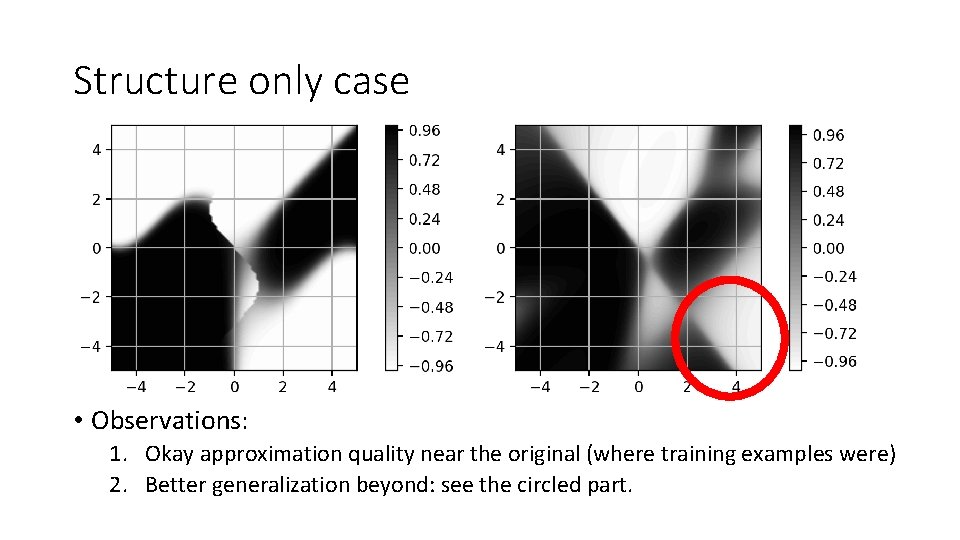
Structure only case • Observations: 1. Okay approximation quality near the original (where training examples were) 2. Better generalization beyond: see the circled part.

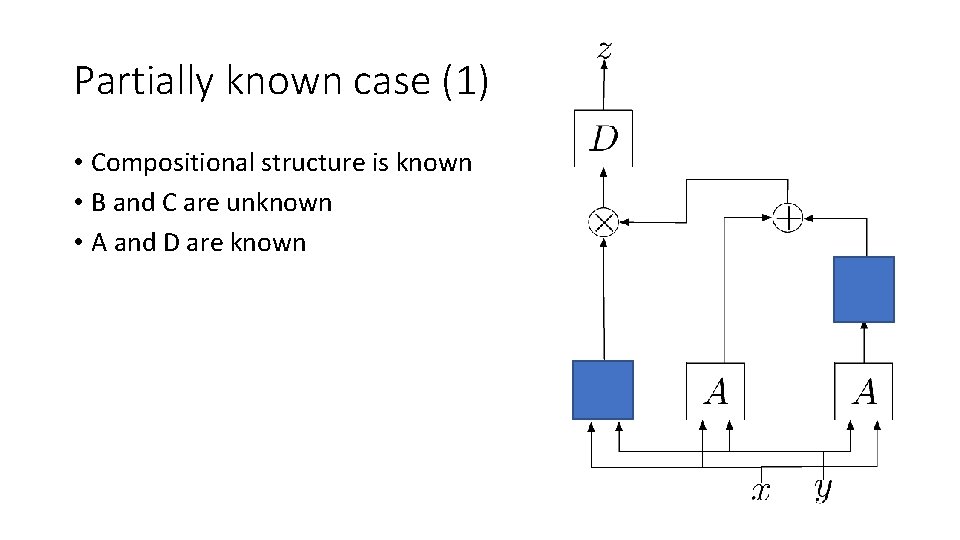
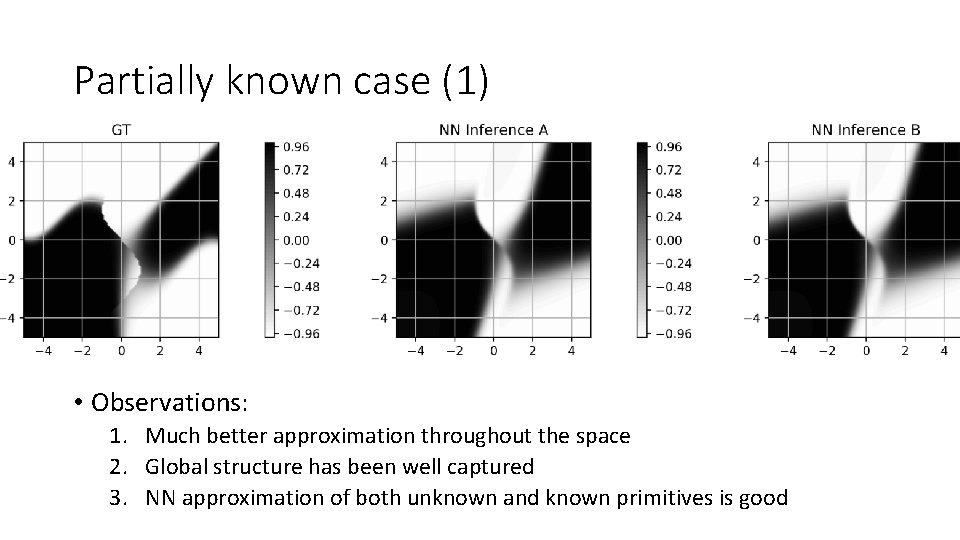
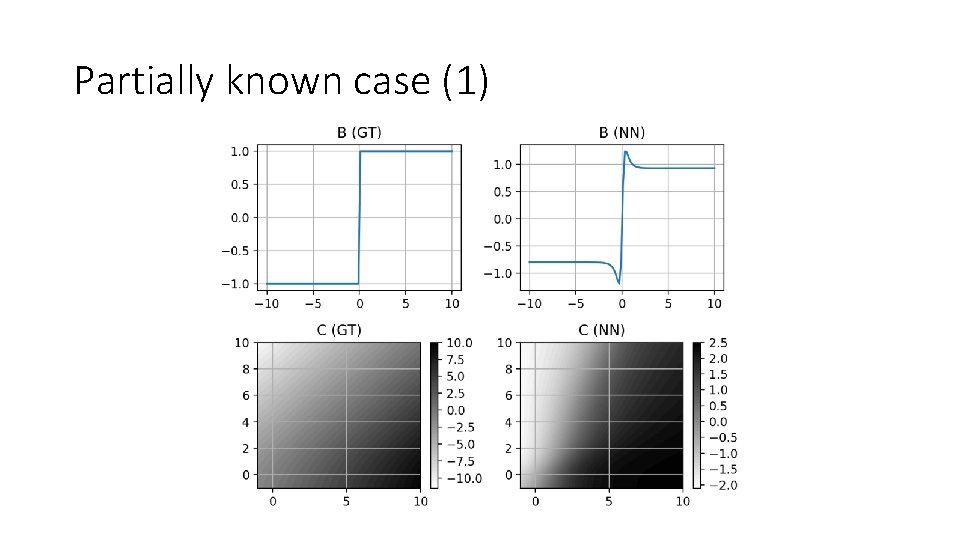
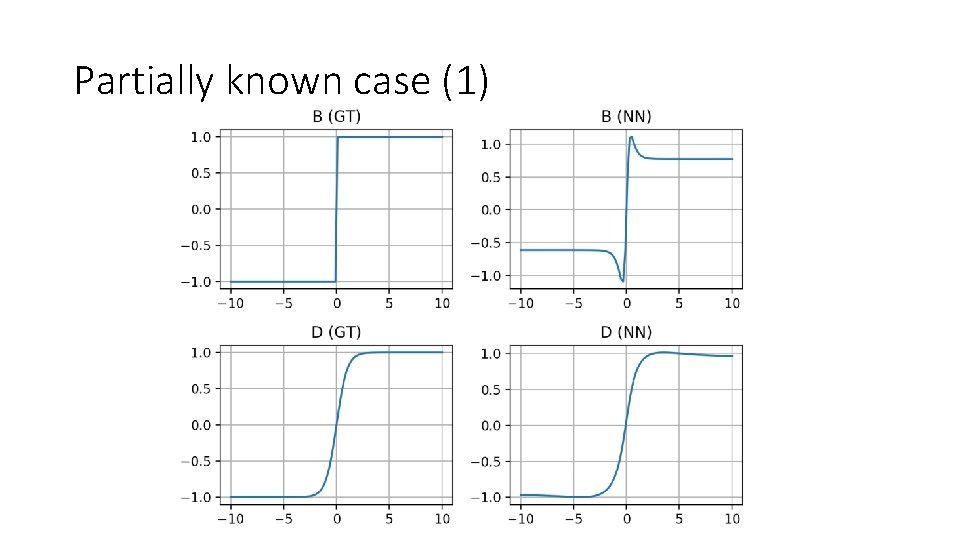
Partially known case (1) • Compositional structure is known • B and C are unknown • A and D are known

Partially known case (1) • Observations: 1. Much better approximation throughout the space 2. Global structure has been well captured 3. NN approximation of both unknown and known primitives is good

Partially known case (1)

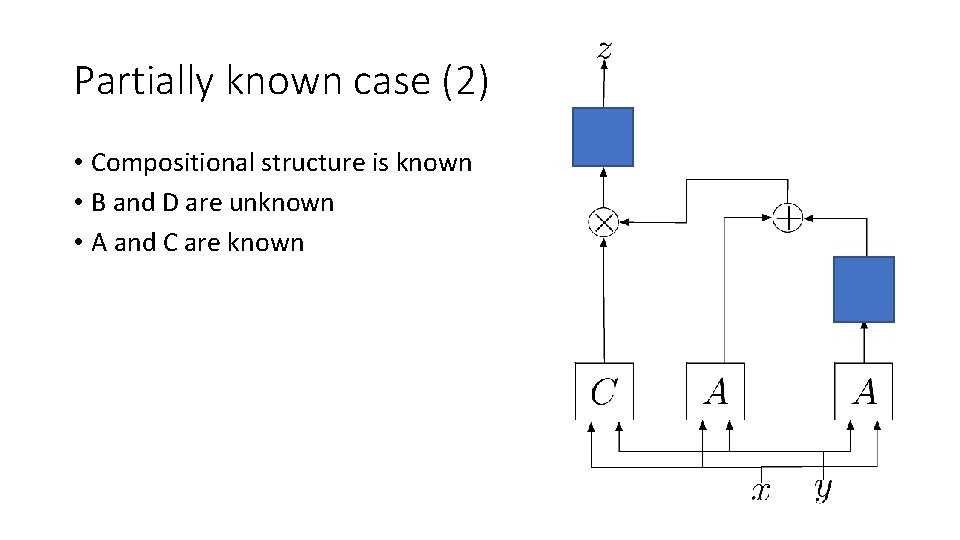
Partially known case (2) • Compositional structure is known • B and D are unknown • A and C are known

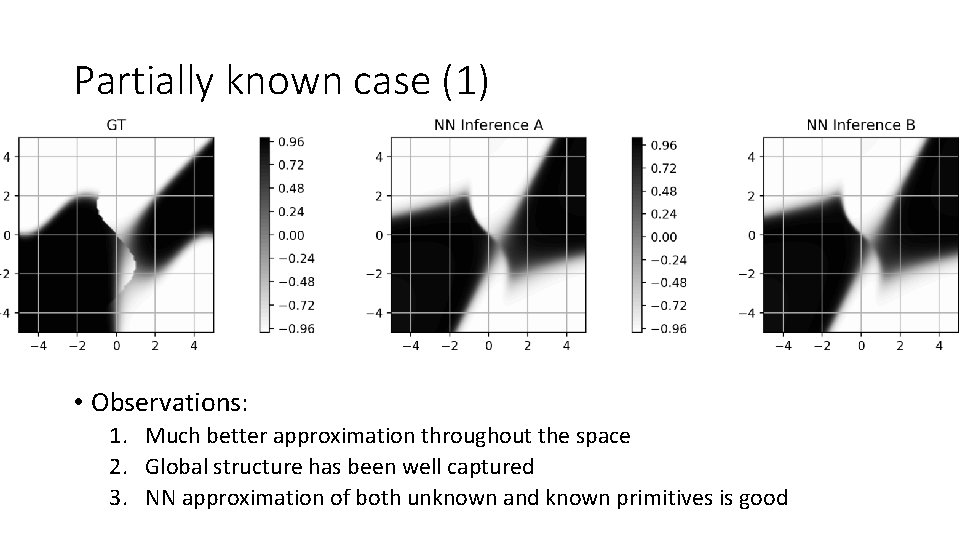
Partially known case (1) • Observations: 1. Much better approximation throughout the space 2. Global structure has been well captured 3. NN approximation of both unknown and known primitives is good

Partially known case (1)

Conclusion • Neural networks are flexible function approximators • Allows us to follow a known, underlying compositional structure • Allows us to fill in the gaps of an arbitrary generating process • With latest DL toolkits, much of this process can be automated • Py. Torch, Dy. Net, Min. Py (Mx. Net), Theano, Tensor. Flow, …

Future Direction • Stochastic generating process: beyond unimodal posterior • NN approximation of a primitive function by VAE [Kingma & Welling, 2014] or GAN [Goodfellow et al. , 2015] • Uncertainty propagation • Bayes-by-Backprop [Blundell et al. , 2016], Dropout as Bayes Approx [Gal & Ghahramani, 2016] and many earlier and recent work • Explicit bias removal • Domain-adversarial training of neural networks [Ganin et al. , 2016] • Learn to pivot with adversarial networks [Louppe et al. , 2016] • When the underlying compositional structure is unknown… • Black-box, combinatorial optimization for finding a structure: Hyper. Opt [Bergstra et al. , 2013], … • Softer, differentiable approximation to structure optimization: Attention model, DNC [Graves et al. , 2016], …