DSC 3120 Generalized Modeling Techniques with Applications Part

DSC 3120 Generalized Modeling Techniques with Applications Part III. Decision Analysis 1

Decision Analysis u A Rational and Systematic Approach to Decision Making u Decision Making: choose the “best” from several available alternative courses of action u Key Element is Uncertainty of the outcome • We, as decision maker, control the decision • Outcome of the decision is uncertain to and uncontrolled by decision maker (controlled by nature) Decision Analysis 2

Example of Decision Analysis You have $10, 000 for investing in one of the three options: Stock, Mutual Fund, and CD. What is the best choice? Question: Do you know the choices? Do you know the best choice? What is the uncertainty? How do you make your choice? Decision Analysis 3

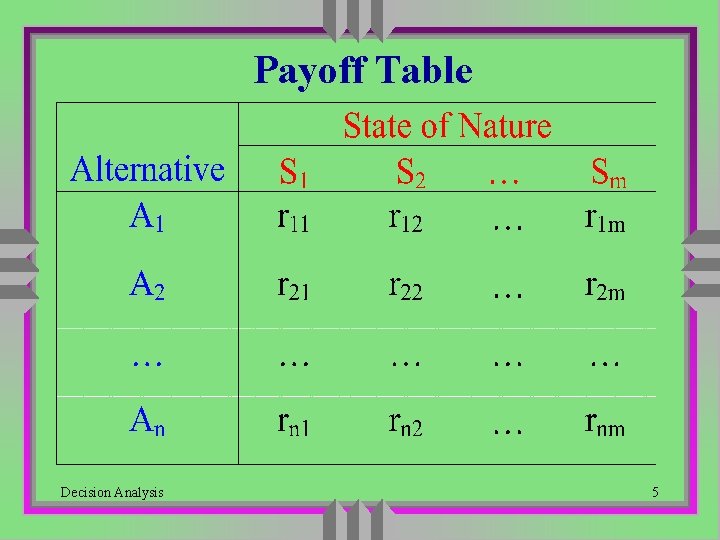
Components of Decision Problem u Alternative Actions -- Decisions • There are several alternatives from which we want to choose the best u States of Nature -- Outcomes • There are several possible outcomes but which one will occur is uncertain to us u Payoffs • Numerical (monetary) value representing the consequence of a particular alternative action we choose and a state of nature that occurs later on Decision Analysis 4

Payoff Table Decision Analysis 5

An Example Alternative State of Nature Decision Analysis 6

Three Classes of Decision Models u Decision Making Under Certainty • Only one state of nature (or we know with 100% sure what will happen) u Decision Making Under Uncertainty (ignorance) • Several possible states of nature, but we have no idea about the likelihood of each possible state u Decision Making Under Risk • Several possible states of nature, and we have an estimate of the probability for each state Decision Analysis 7

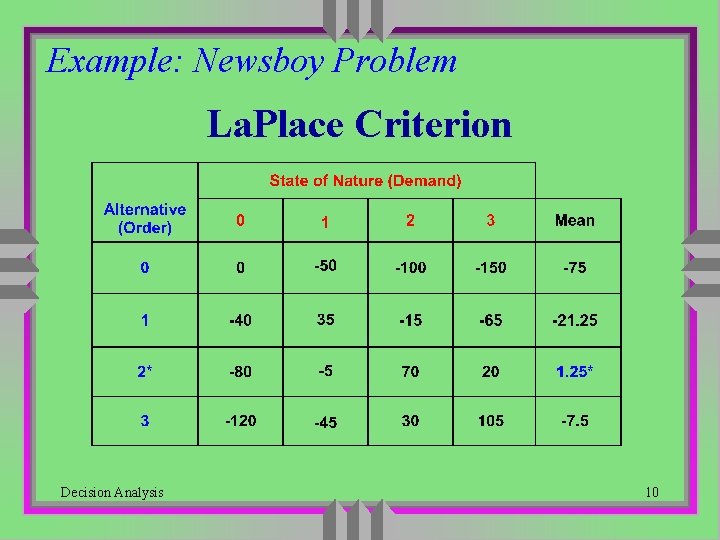
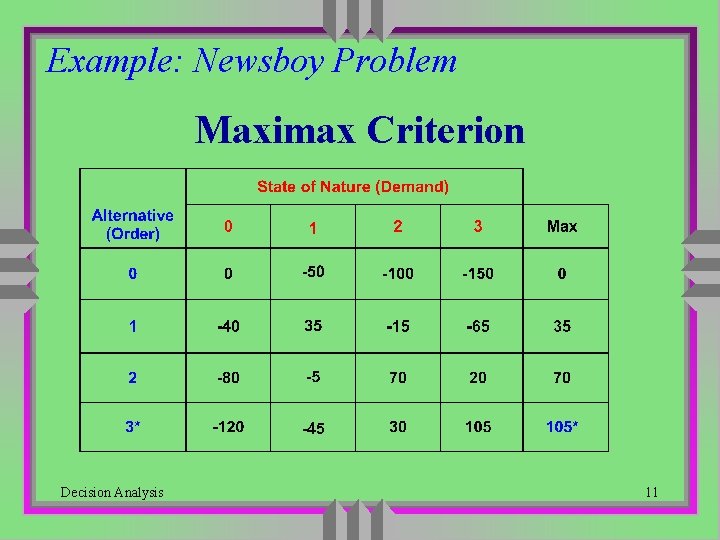
Decision Making Under Uncertainty u La. Place (Assume Equal Likely States of Nature) • Select alternative with best average payoff u Maximax (Assume The Best State of Nature) • Select alternative that will maximize the maximum payoff (expect the best outcome--optimistic) u Maximin (Assume The Worst State of Nature) • Select alternative that will maximize the minimum payoff (expect the worst situation--pessimistic) u Minimax Regret (Don’t Want to Regret Too Much) • Select alternative that will minimize the maximum regret Decision Analysis 8

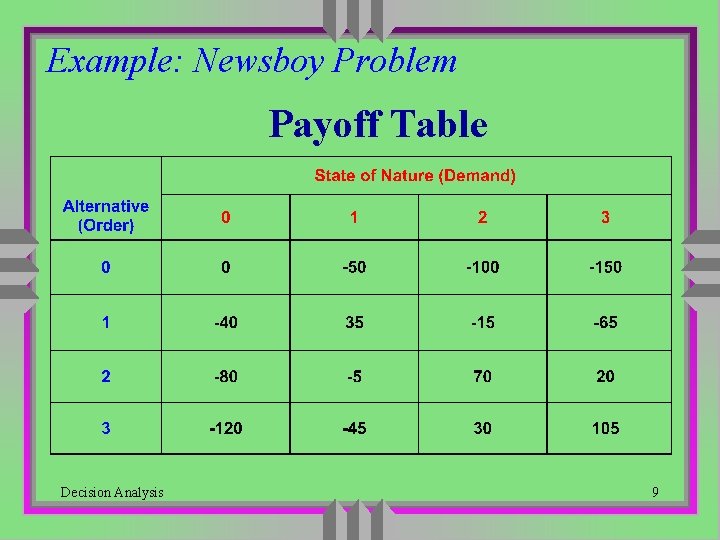
Example: Newsboy Problem Payoff Table Decision Analysis 9

Example: Newsboy Problem La. Place Criterion Decision Analysis 10

Example: Newsboy Problem Maximax Criterion Decision Analysis 11

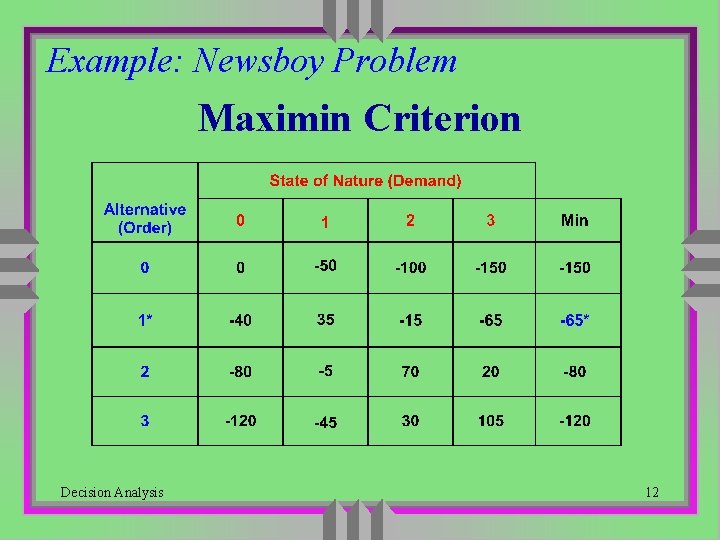
Example: Newsboy Problem Maximin Criterion Decision Analysis 12

Example: Newsboy Problem Minimax Regret Criterion: Step 1 Decision Analysis 13

Example: Newsboy Problem Minimax Regret: Step 2 (Regret or Opportunity Loss Table) Decision Analysis 14

Decision Making Under Risk • In this situation, we have more information about the uncertainty--probability Decision Analysis 15

Decision Making Under Risk u. Maximize Expected Return (ER) ERi = (pj rij) = p 1 ri 1 + p 2 ri 2 +…+ pmrim Where ERi = Expected return if choosing the ith alternative (Ai), (i = 1, 2, …, n) pj = The probability of state j (Sj) rij = The payoff if we choose alternative Ai and Sj state of nature occurs Decision Analysis 16

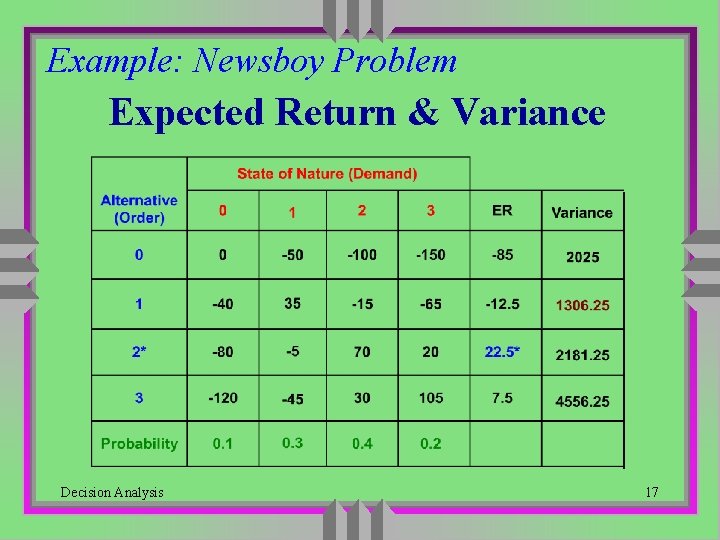
Example: Newsboy Problem Expected Return & Variance Decision Analysis 17

Decision Making Under Risk u. High return is good, but on the other hand, low risk is also important u. Variance -- a measure of the risk Variancei = pj (rij - ERi)2 Where pj = The probability of state j (Sj) rij = The payoff if choose Ai and Sj occurs ERi= Expected return for alternative Ai Decision Analysis 18

Expected Value of Perfect Information u EVPI measures the maximum worth (value) of the “Perfect Information” that we should pay for in order to improve our decisions EVPI = ER w/ perfect info. - ER w/o perfect info. • ER w/ perfect info. = pj max(rij) • ER w/o perfect info. = max(ERi) = max( pj rij) Decision Analysis 19

Example: Newsboy Problem Calculate EVPI ER w/o PI ER w/ PI EVPI Decision Analysis 20

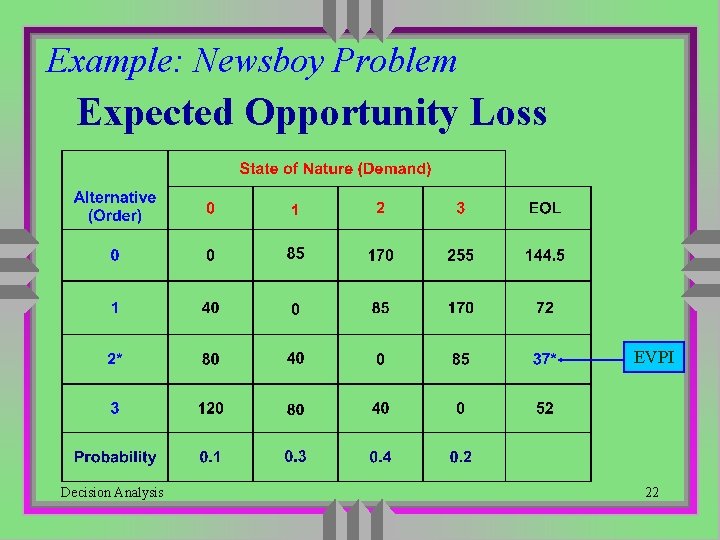
Expected Opportunity Loss (EOL) u We can also use EOL to choose the best alternative u Minimizing EOL = Maximizing ER • both criteria yield the same best alternative EOLi = pj OLij where pj = The probability of state j (Sj) OLij = The opportunity loss if choose Ai and Sj occurs s min(EOLi) = EVPI Decision Analysis 21

Example: Newsboy Problem Expected Opportunity Loss EVPI Decision Analysis 22

Decision Making with Utilities u Problem with Monetary Payoffs • People do not always just look at the highest expected monetary return to make decisions; they often evaluate the risk • Example: A company wants to decide to develop a new product or not Decision Analysis 23

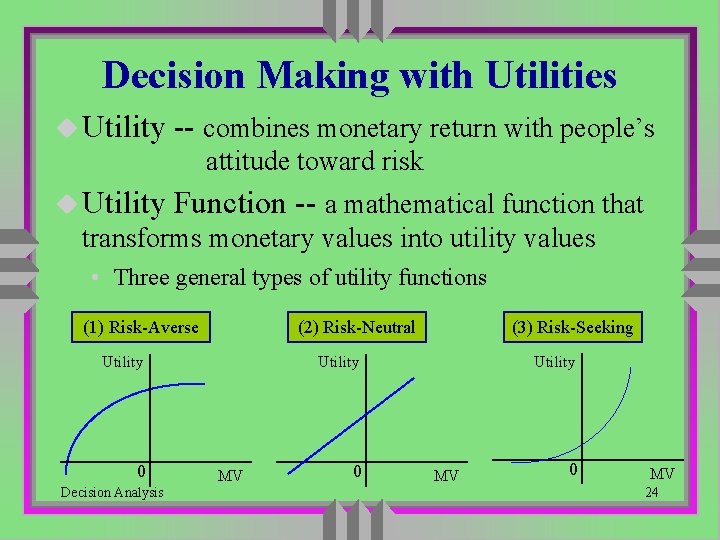
Decision Making with Utilities u Utility -- combines monetary return with people’s attitude toward risk u Utility Function -- a mathematical function that transforms monetary values into utility values • Three general types of utility functions (1) Risk-Averse (2) Risk-Neutral Utility 0 Decision Analysis (3) Risk-Seeking Utility MV 0 MV 24

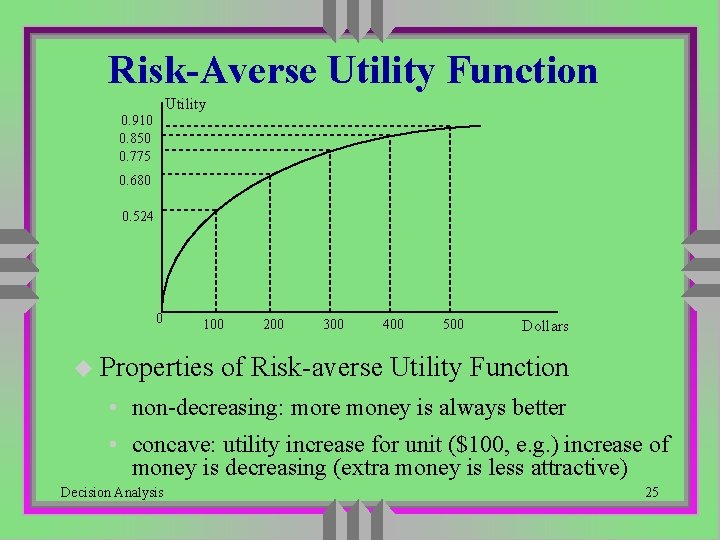
Risk-Averse Utility Function Utility 0. 910 0. 850 0. 775 0. 680 0. 524 0 100 u Properties 200 300 400 500 Dollars of Risk-averse Utility Function • non-decreasing: more money is always better • concave: utility increase for unit ($100, e. g. ) increase of money is decreasing (extra money is less attractive) Decision Analysis 25

How to Create Utility Function u Method I. Equivalent Lottery þ Start with two endpoints A (the worst possible payoff) and B (the best possible payoff) and assign U(A) = 0 and U(B) = 1 þ Then to find the utility for a possible payoff z between A and B, select the probability p (=U(z)) such that you are indifferent between the following two alternatives – receive a payoff of z for sure – receive a payoff of B with probability p or a payoff of A with probability 1 - p Decision Analysis 26

How to Create Utility Function u Method II. Exponential Utility Function where x is the monetary value, r>0 is an adjustable parameter called risk tolerance þ First, the value of r can be estimated such that we are indifferent between the following choices a payoff of zero þ a payoff of r dollars or a loss of r/2 dollars with 50 -50 chance þ þ Then the utility for a particular monetary value x can be found using the above assumed exponential utility function Decision Analysis 27

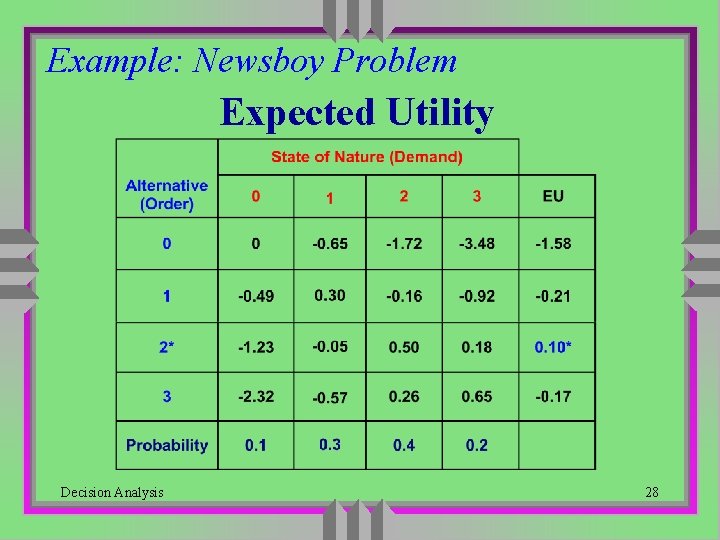
Example: Newsboy Problem Expected Utility Decision Analysis 28