Droites et plans I Dtermination dun plan 1

Droites et plans

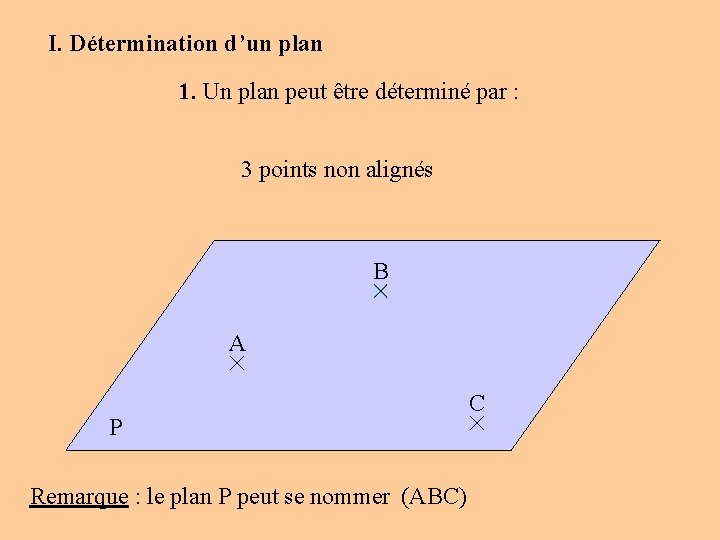
I. Détermination d’un plan 1. Un plan peut être déterminé par : 3 points non alignés B A P Remarque : le plan P peut se nommer (ABC) C

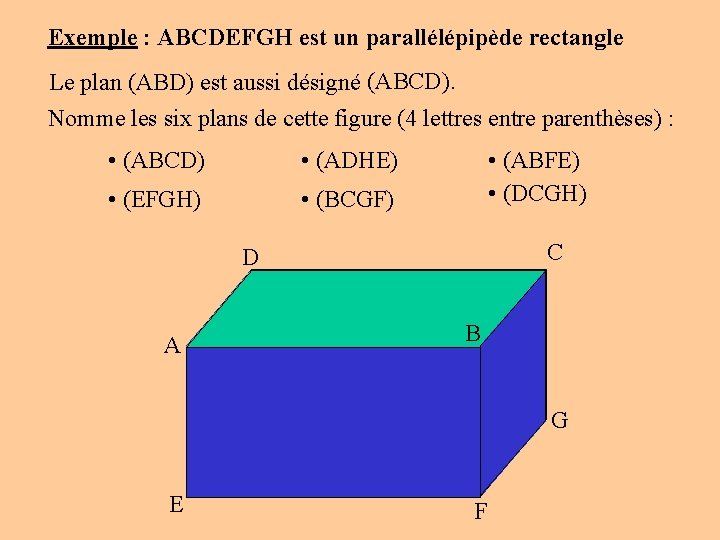
Exemple : ABCDEFGH est un parallélépipède rectangle Le plan (ABD) est aussi désigné (ABCD). Nomme les six plans de cette figure (4 lettres entre parenthèses) : • (ABCD) • (ADHE) • (EFGH) • (BCGF) • (ABFE) • (DCGH) C D B A H E G F

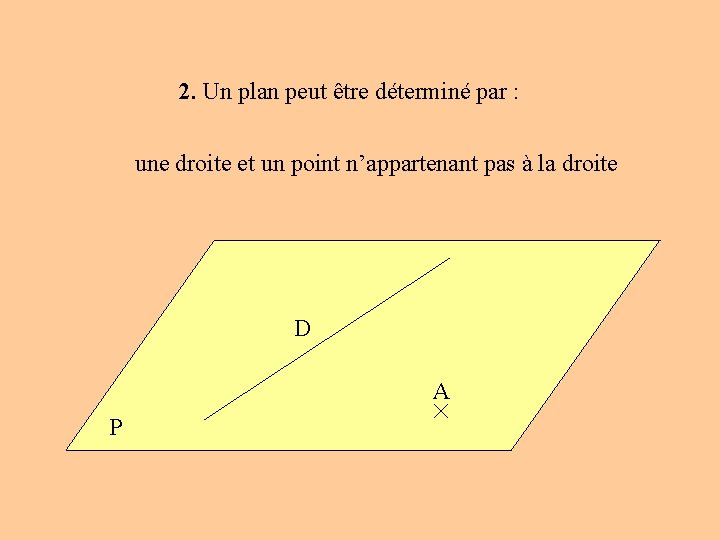
2. Un plan peut être déterminé par : une droite et un point n’appartenant pas à la droite D A P

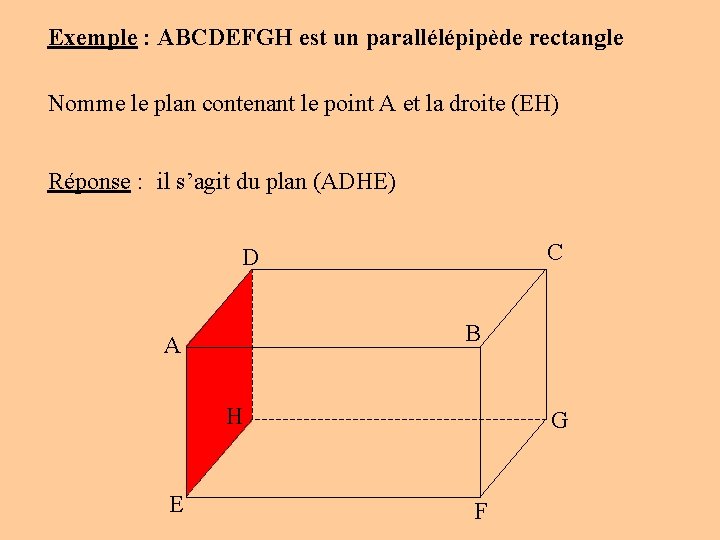
Exemple : ABCDEFGH est un parallélépipède rectangle Nomme le plan contenant le point A et la droite (EH) Réponse : il s’agit du plan (ADHE) C D B A H E G F

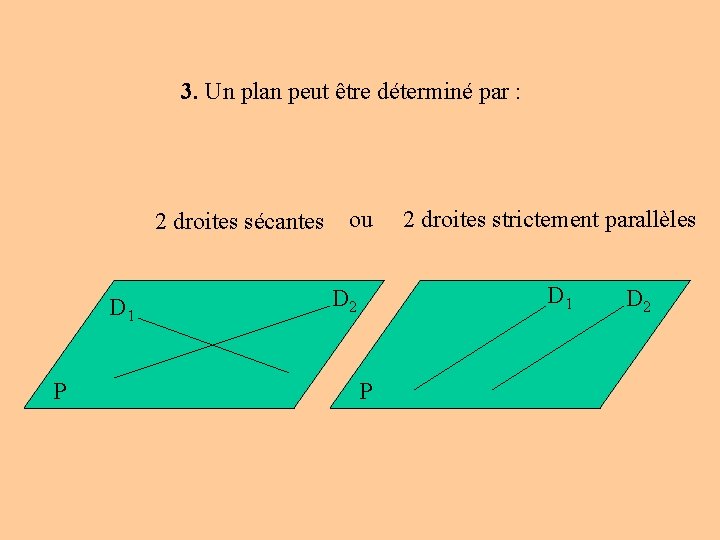
3. Un plan peut être déterminé par : 2 droites sécantes D 1 P ou 2 droites strictement parallèles D 1 D 2 P D 2

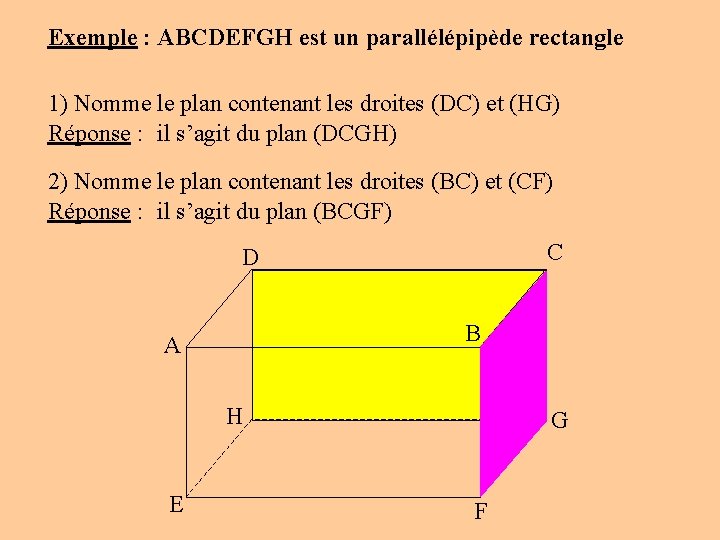
Exemple : ABCDEFGH est un parallélépipède rectangle 1) Nomme le plan contenant les droites (DC) et (HG) Réponse : il s’agit du plan (DCGH) 2) Nomme le plan contenant les droites (BC) et (CF) Réponse : il s’agit du plan (BCGF) C D B A H E G F

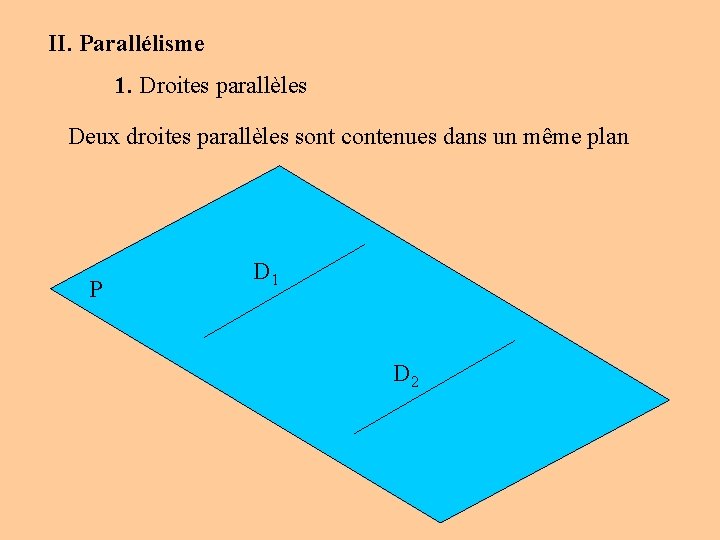
II. Parallélisme 1. Droites parallèles Deux droites parallèles sont contenues dans un même plan P D 1 D 2

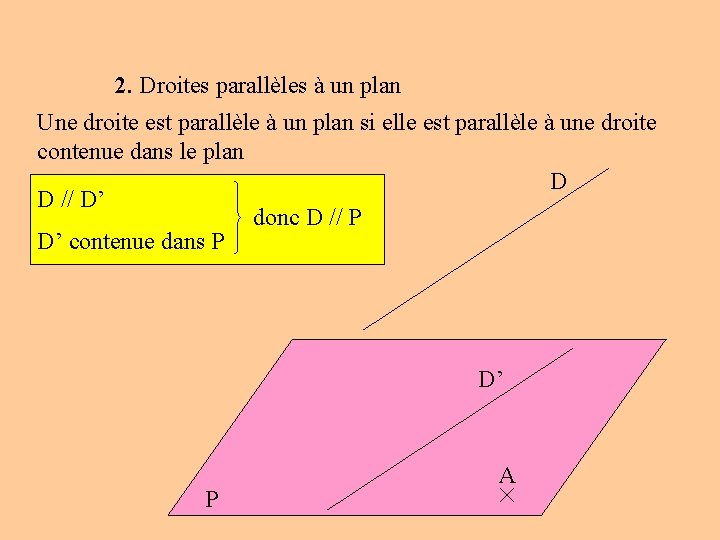
2. Droites parallèles à un plan Une droite est parallèle à un plan si elle est parallèle à une droite contenue dans le plan D D // D’ donc D // P D’ contenue dans P D’ P A

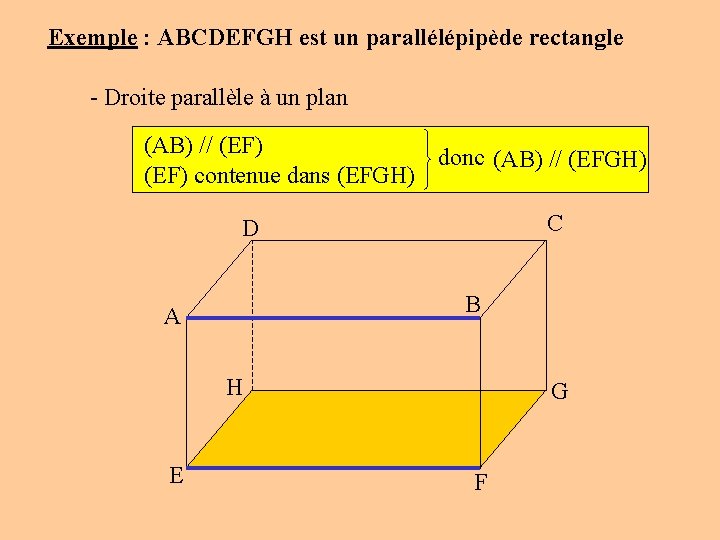
Exemple : ABCDEFGH est un parallélépipède rectangle - Droite parallèle à un plan (AB) // (EF) donc (AB) // (EFGH) (EF) contenue dans (EFGH) C D B A H E G F

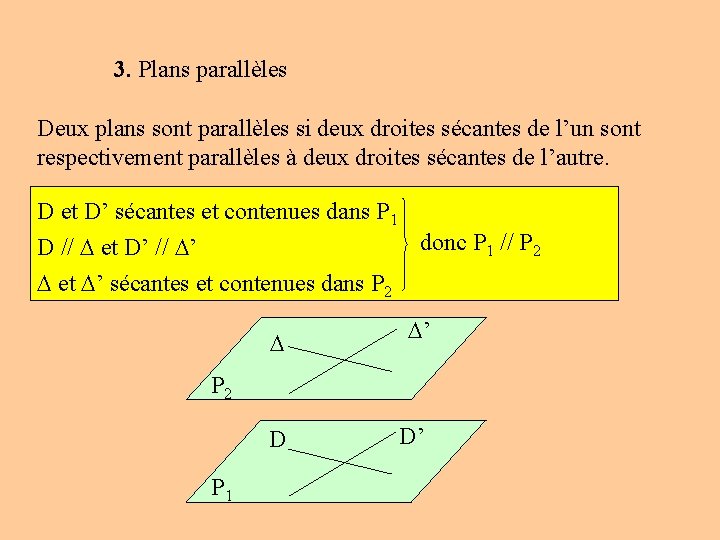
3. Plans parallèles Deux plans sont parallèles si deux droites sécantes de l’un sont respectivement parallèles à deux droites sécantes de l’autre. D et D’ sécantes et contenues dans P 1 donc P 1 // P 2 D // et D’ // ’ et ’ sécantes et contenues dans P 2 ’ P 2 D P 1 D’

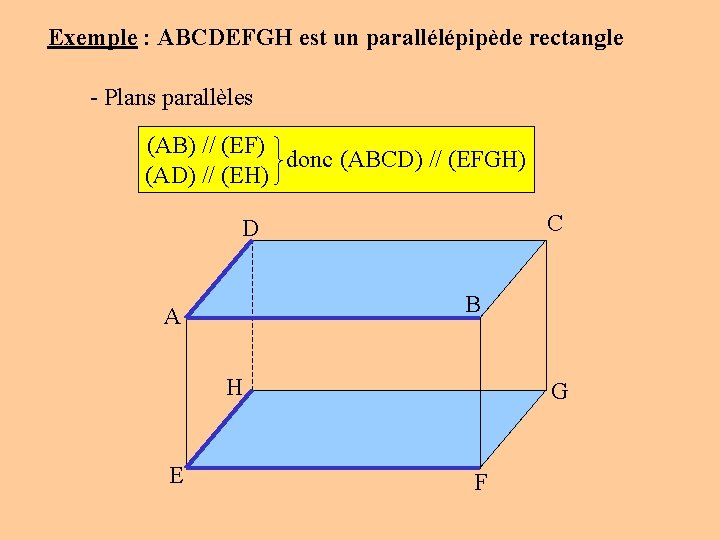
Exemple : ABCDEFGH est un parallélépipède rectangle - Plans parallèles (AB) // (EF) donc (ABCD) // (EFGH) (AD) // (EH) C D B A H E G F

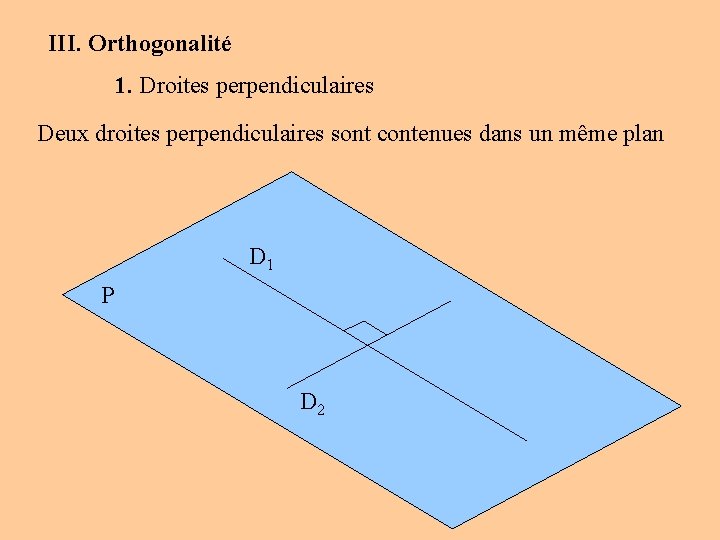
III. Orthogonalité 1. Droites perpendiculaires Deux droites perpendiculaires sont contenues dans un même plan D 1 P D 2

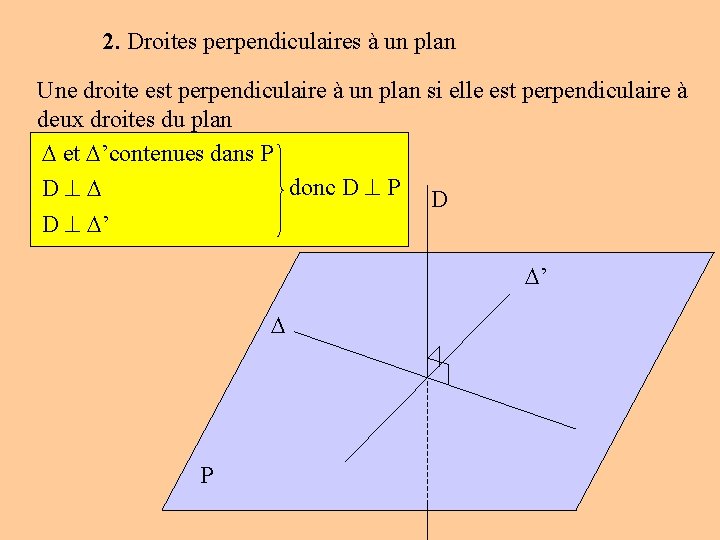
2. Droites perpendiculaires à un plan Une droite est perpendiculaire à un plan si elle est perpendiculaire à deux droites du plan et ’contenues dans P donc D P D D D ’ ’ P

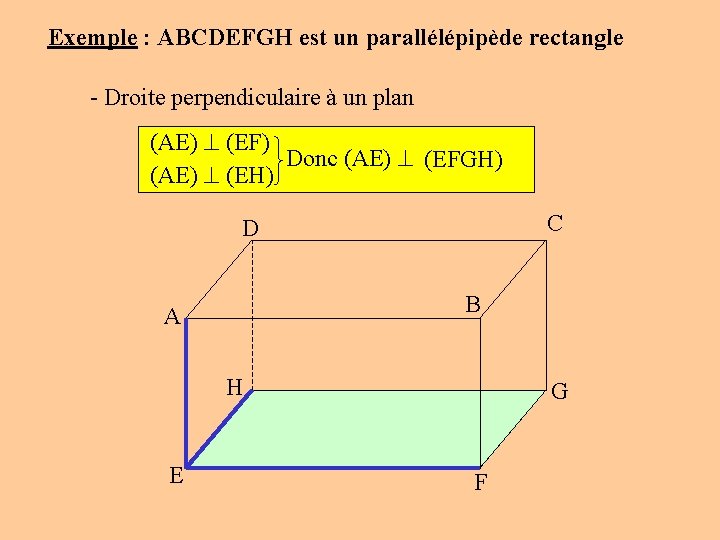
Exemple : ABCDEFGH est un parallélépipède rectangle - Droite perpendiculaire à un plan (AE) (EF) Donc (AE) (EFGH) (AE) (EH) C D B A H E G F

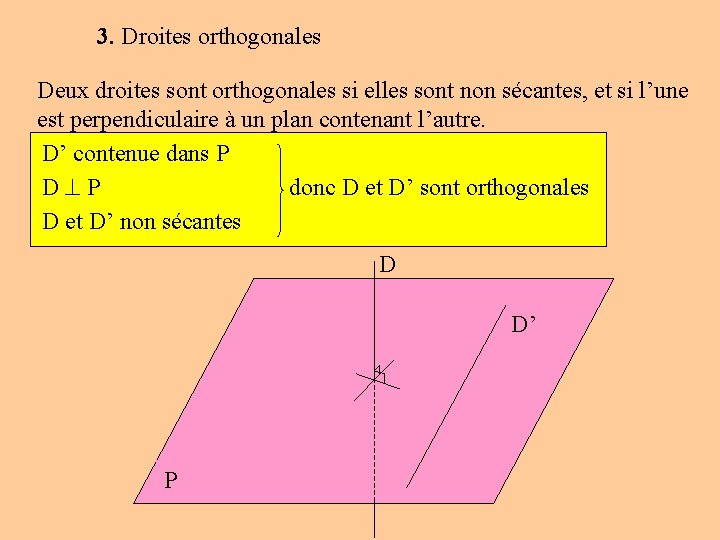
3. Droites orthogonales Deux droites sont orthogonales si elles sont non sécantes, et si l’une est perpendiculaire à un plan contenant l’autre. D’ contenue dans P D P donc D et D’ sont orthogonales D et D’ non sécantes D D’ P

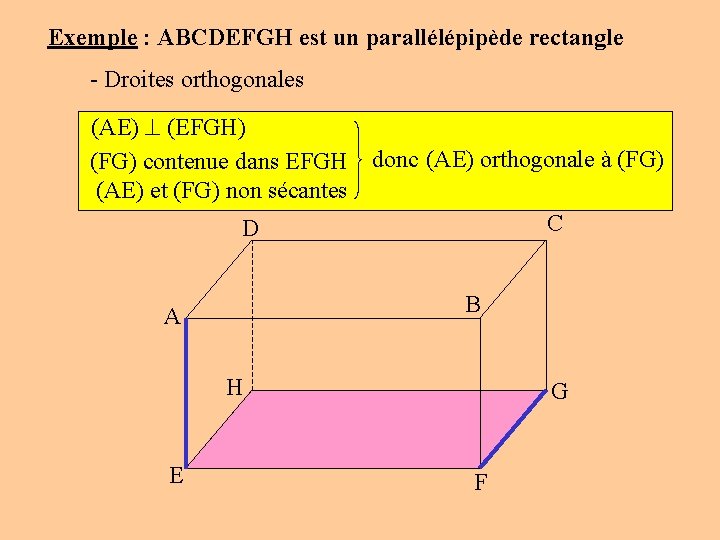
Exemple : ABCDEFGH est un parallélépipède rectangle - Droites orthogonales (AE) (EFGH) (FG) contenue dans EFGH (AE) et (FG) non sécantes donc (AE) orthogonale à (FG) C D B A H E G F

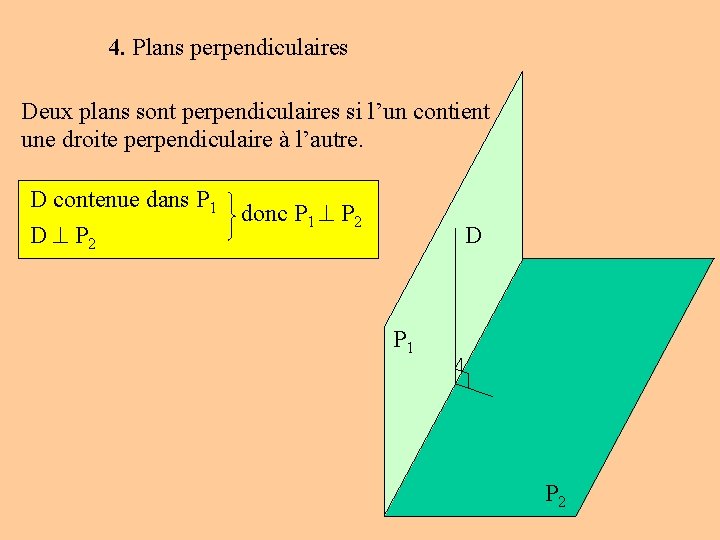
4. Plans perpendiculaires Deux plans sont perpendiculaires si l’un contient une droite perpendiculaire à l’autre. D contenue dans P 1 D P 2 donc P 1 P 2 D P 1 P 2

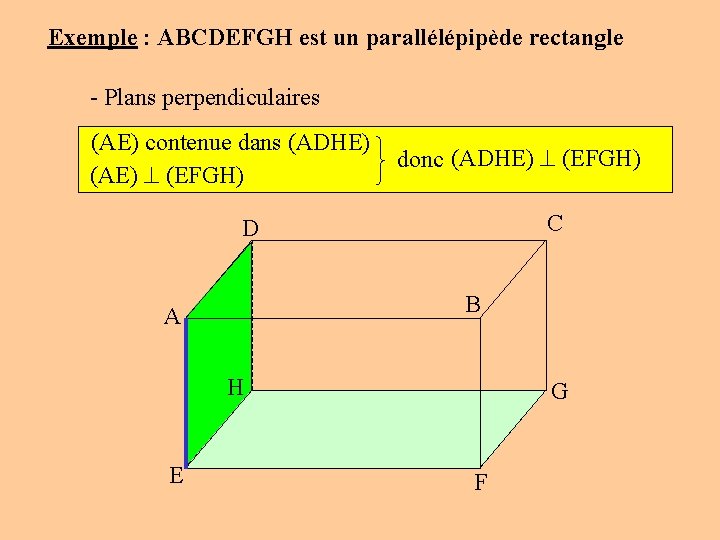
Exemple : ABCDEFGH est un parallélépipède rectangle - Plans perpendiculaires (AE) contenue dans (ADHE) (AE) (EFGH) donc (ADHE) (EFGH) C D B A H E G F

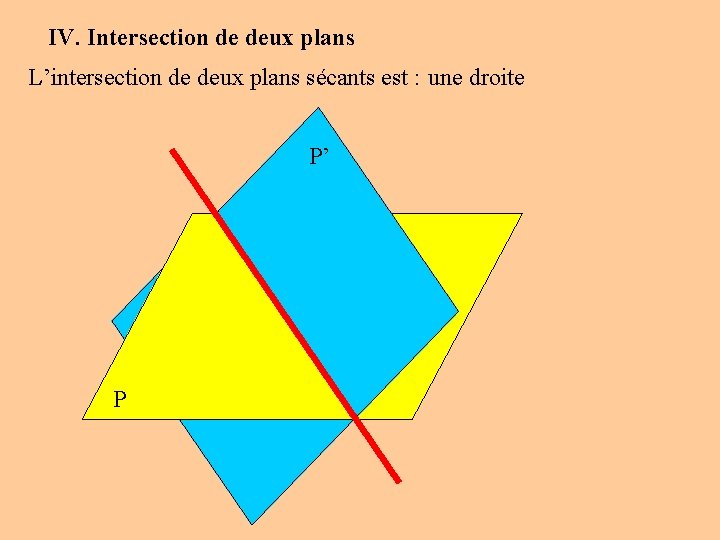
IV. Intersection de deux plans L’intersection de deux plans sécants est : une droite P’ P

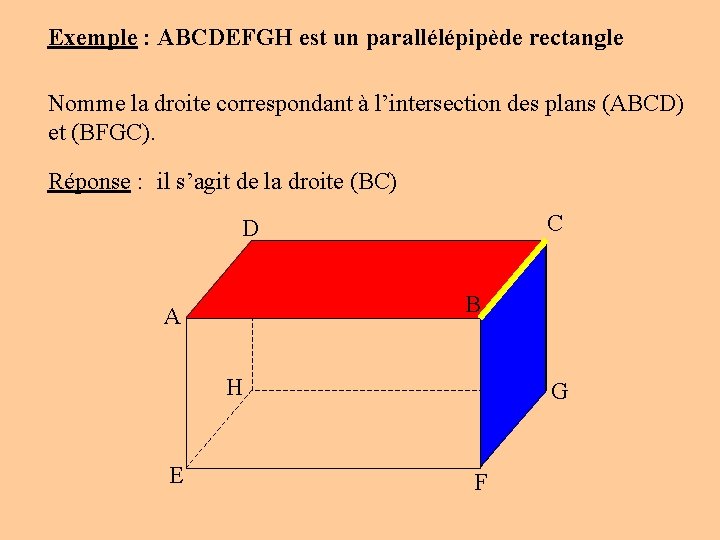
Exemple : ABCDEFGH est un parallélépipède rectangle Nomme la droite correspondant à l’intersection des plans (ABCD) et (BFGC). Réponse : il s’agit de la droite (BC) C D B A H E G F