DRILL 1 The graph below shows the cost

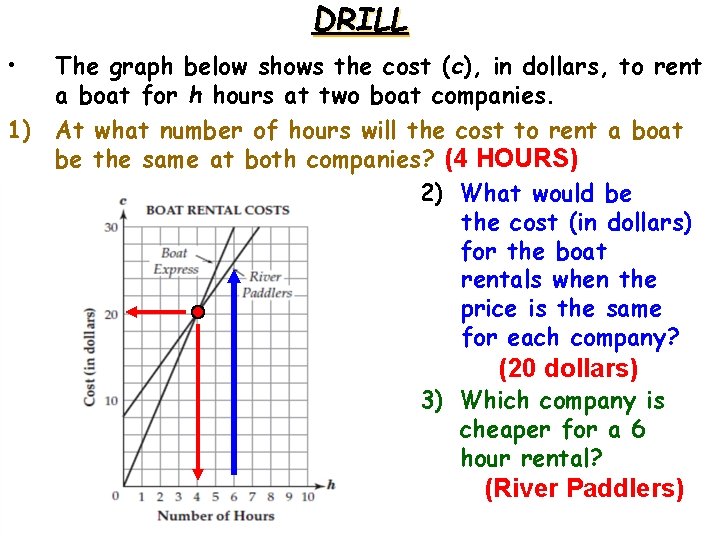
DRILL • 1) The graph below shows the cost (c), in dollars, to rent a boat for h hours at two boat companies. At what number of hours will the cost to rent a boat be the same at both companies? (4 HOURS) 2) What would be the cost (in dollars) for the boat rentals when the price is the same for each company? (20 dollars) 3) Which company is cheaper for a 6 hour rental? (River Paddlers)

Relations and Functions Objectives: • State the domain and range of a relation, and tell whether it is a function • Write a function in function notation and evaluate it

Textbook Definitions Into Our Definitions A Relation is a set of ordered pairs. The set of the first coordinates is called the domain of the relation. The set of the second coordinates is called the range of the relation. A Function is a relation in which each element of the domain is paired with exactly one element in the range.

Definitions • Relation: A relation is any set of ordered pairs. Ex: {(-2, 3) (3, -8) (5, 7) (5, 10)} • Function: A function is a relation where each x-value (input) corresponds to exactly one y-value (output). Ex: {(-2, 3) (3, -8) (5, 7) (8, 10)}

Definitions Domain: set of all possible values of the first variable (x-values) Range: set of all possible values of the second variable (y-values)

Examples 1) {(2, 4) (3, 5) (3, 6) (7, 9)} Not a Function 2) {(2, 4) (4, 5) (6, 8) (7, 9)} Function 3) {(1, 2) (3, 5) (7, 6) (8, 9)} Function 4) {(2, 4) (8, 5) (8, 6) (11, 9)} Not a Function 5) {(0, 1) (1, 1) (2, 1) (3, 1)} Function

Example 1 State the domain and range of the relation, and state whether it is a function. { (– 7, 5), (4, 12), (8, 23), (16, 8) } domain: { – 7, 4, 8, 16} range: { 5, 8, 12, 23 } This is a function because each x-coordinate is paired with only one y-coordinate.

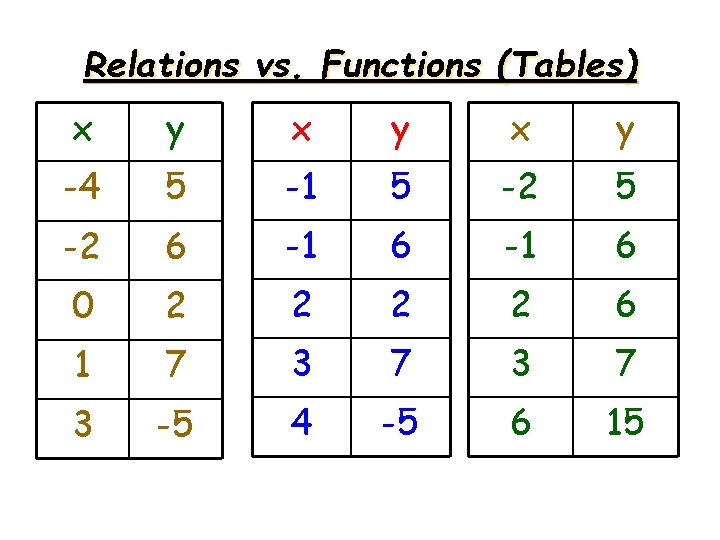
Relations vs. Functions (Tables) x y x y -4 5 -1 5 -2 6 -1 6 0 2 2 6 1 7 3 7 3 -5 4 -5 6 15

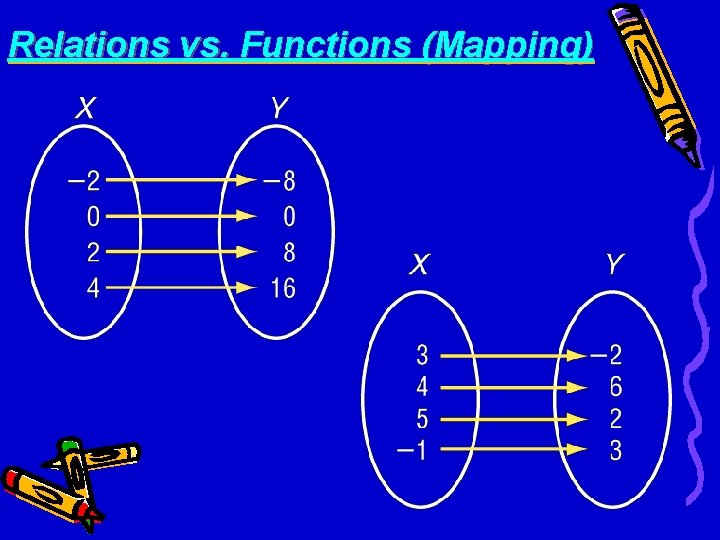
Relations vs. Functions (Mapping)

Example 2 State whether the data in each table represents y as a function of x. Explain. x y 2 2 3 4 4 3 3 5 6 4 5 -4 8 5 6 3 function not a function

Vertical Line Test • What type of lines would pass through the x-axis every time? (Horizontal or Vertical) • The vertical line test says: if you can draw a vertical line through more than one point on a graph, then it is NOT a function.

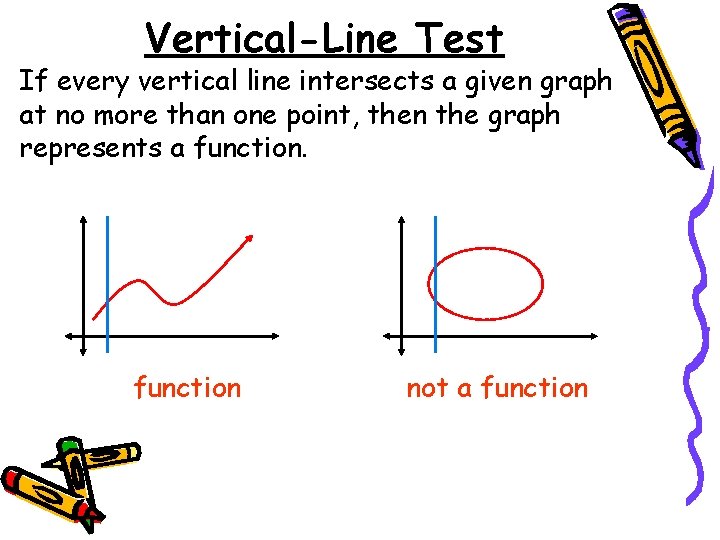
Vertical-Line Test If every vertical line intersects a given graph at no more than one point, then the graph represents a function not a function

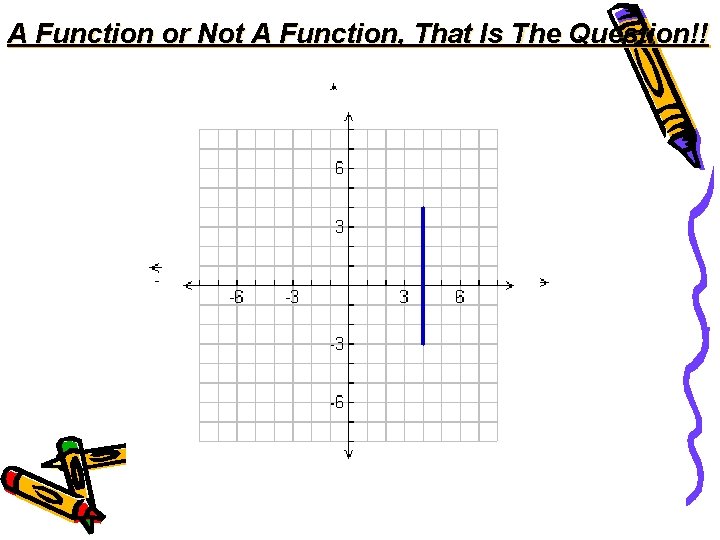
A Function or Not A Function, That Is The Question!!

Function Notation If there is a correspondence between values of the domain, x, and values of the range, y, that is a function, then y = f(x), and (x, y) can be written as (x, f(x)). The variable x is called the independent variable. The variable y, or f(x) is called the dependent variable.

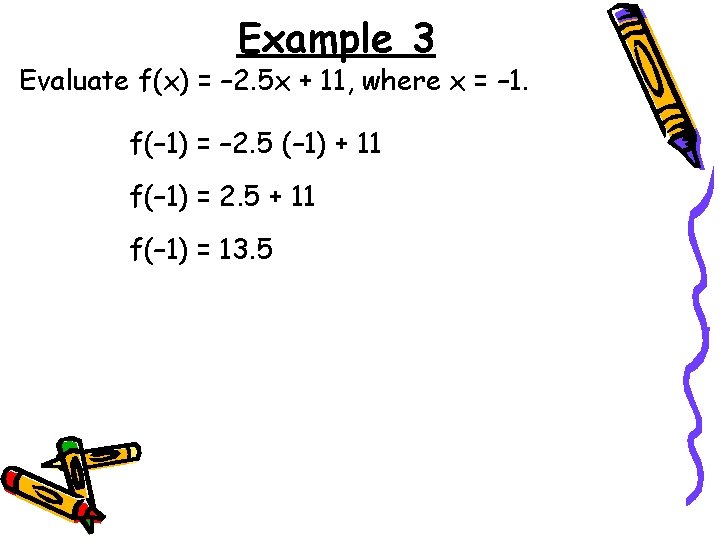
Example 3 Evaluate f(x) = – 2. 5 x + 11, where x = – 1. f(– 1) = – 2. 5 (– 1) + 11 f(– 1) = 2. 5 + 11 f(– 1) = 13. 5

Practice Find the indicated outputs. 1) f(x) = x + 3; find f(5), f(-8), and f(-2). 2) g(x) = 3 x – x 2; find g(0), g(-2), and g(1). 3) p(x) = 2 x 2 + x - 1; find p(0), p(-2), and p(3).

Example 4 A gift shop sells a specialty fruit and nut mix at a cost of $2. 99 per pound. During the holiday season, you can buy as much of the mix as you like and have it packaged in a decorative tin that costs $4. 95. a) Write a linear function to model the total cost in dollars, c, of the tin containing the fruit and nut mix as a function of the number of pounds of the mix, n. c(n) = 4. 95 + 2. 99 n b) Find the total cost of a tin that contains 1. 5 pounds of the mix. c(n) = 4. 95 + 2. 99 n c(1. 5) = 4. 95 + 2. 99(1. 5) c(1. 5) = 9. 44 $9. 44

Functions Domain and Range

Functions vs. Relations • A "relation" is just a relationship between sets of information. • A “function” is a well-behaved relation, that is, given a starting point we know exactly where to go.

Example • People and their heights, i. e. the pairing of names and heights. • We can think of this relation as ordered pair: • (height, name) • Or • (name, height)

Example (continued) Name Height Joe=1 6’=6 Mike=2 5’ 9”=5. 75 Rose=3 5’=5 Kiki=4 5’=5 Jim=5 6’ 6”=6. 5

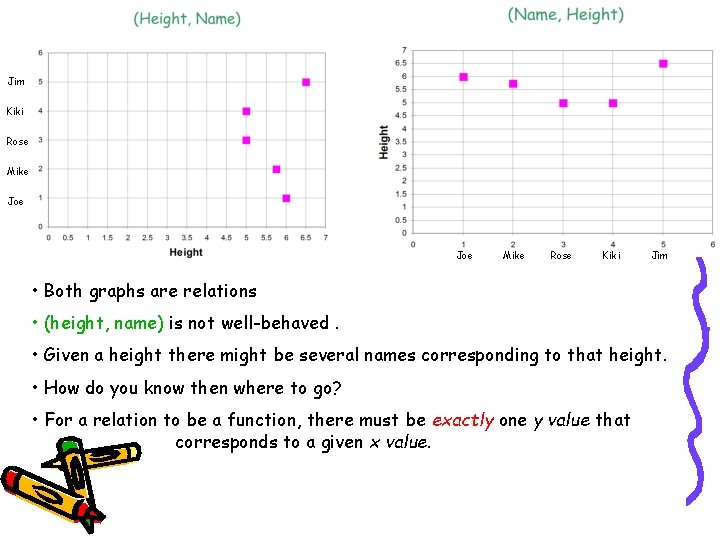
Jim Kiki Rose Mike Joe Mike Rose Kiki Jim • Both graphs are relations • (height, name) is not well-behaved. • Given a height there might be several names corresponding to that height. • How do you know then where to go? • For a relation to be a function, there must be exactly one y value that corresponds to a given x value.

Conclusion and Definition • Not every relation is a function. • Every function is a relation. • Definition: Let X and Y be two nonempty sets. A function from X into Y is a relation that associates with each element of X exactly one element of Y.

• Recall, the graph of (height, name): What happens at the height = 5?

Vertical-Line Test • A set of points in the xy-plane is the graph of a function if and only if every vertical line intersects the graph in at most one point.

Representations of Functions • • Verbally Numerically, i. e. by a table Visually, i. e. by a graph Algebraically, i. e. by an explicit formula

• Ones we have decided on the representation of a function, we ask the following question: • What are the possible x-values (names of people from our example) and y-values (their corresponding heights) for our function we can have?

• Recall, our example: the pairing of names and heights. • x=name and y=height • We can have many names for our x-value, but what about heights? • For our y-values we should not have 0 feet or 11 feet, since both are impossible. • Thus, our collection of heights will be greater than 0 and less that 11.

• We should give a name to the collection of possible x-values (names in our example) • And • To the collection of their corresponding y-values (heights). • Everything must have a name

• Variable x is called independent variable • Variable y is called dependent variable • For convenience, we use f(x) instead of y. • The ordered pair in new notation becomes: • (x, y) = (x, f(x)) Y=f(x) x

Domain and Range • Suppose, we are given a function from X into Y. • Recall, for each element x in X there is exactly one corresponding element y=f(x) in Y. • This element y=f(x) in Y we call the image of x. • The domain of a function is the set X. That is a collection of all possible x-values. • The range of a function is the set of all images as x varies throughout the domain.

Our Example • Domain = {Joe, Mike, Rose, Kiki, Jim} • Range = {6, 5. 75, 5, 6. 5}

More Examples • Consider the following relation: • Is this a function? • What is domain and range?

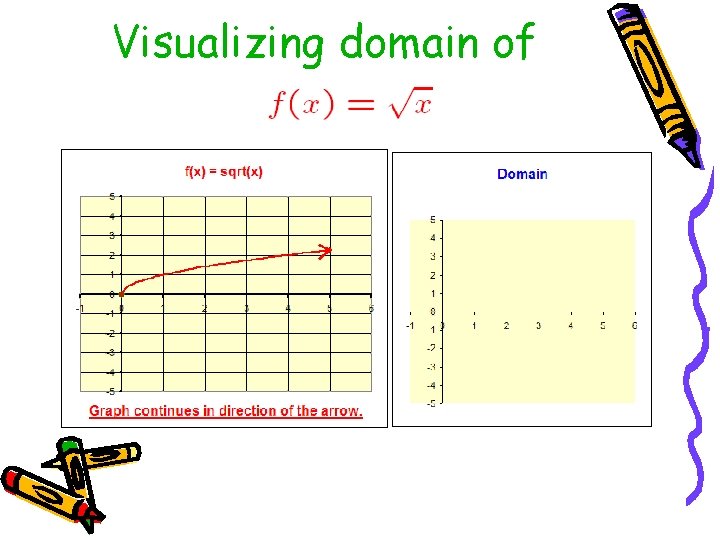
Visualizing domain of

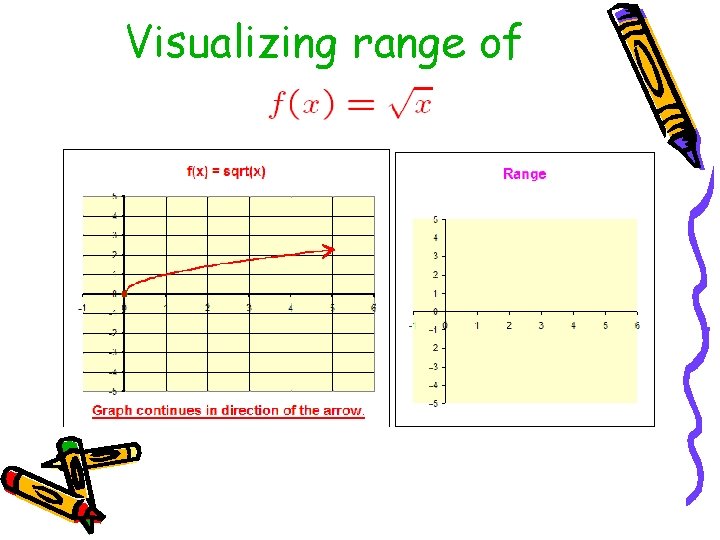
Visualizing range of

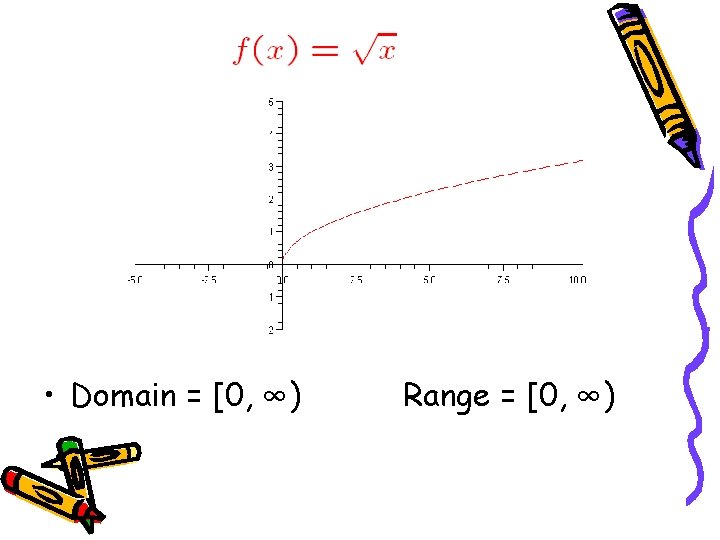
• Domain = [0, ∞) Range = [0, ∞)

More Functions • Consider a familiar function. • Area of a circle: • A(r) = r 2 • What kind of function is this? • Let’s see what happens if we graph A(r).

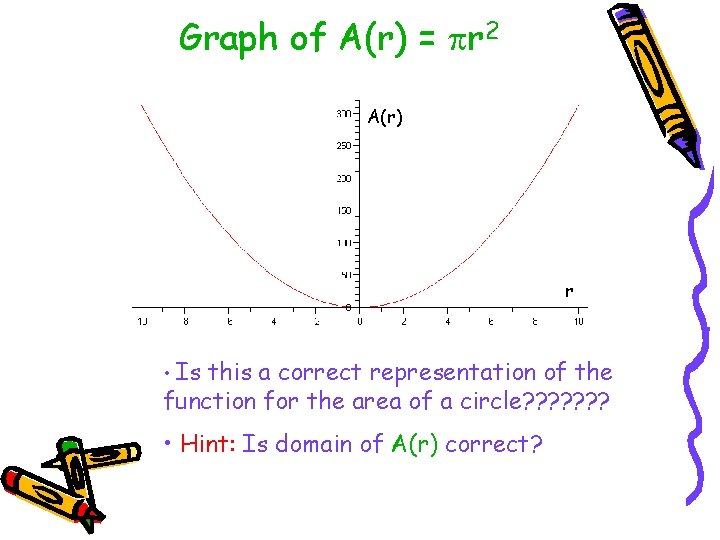
Graph of A(r) = r 2 A(r) r • Is this a correct representation of the function for the area of a circle? ? ? ? • Hint: Is domain of A(r) correct?

Closer look at A(r) = r 2 • Can a circle have r ≤ 0 ? • NOOOOOOO • Can a circle have area equal to 0 ? • NOOOOOOO

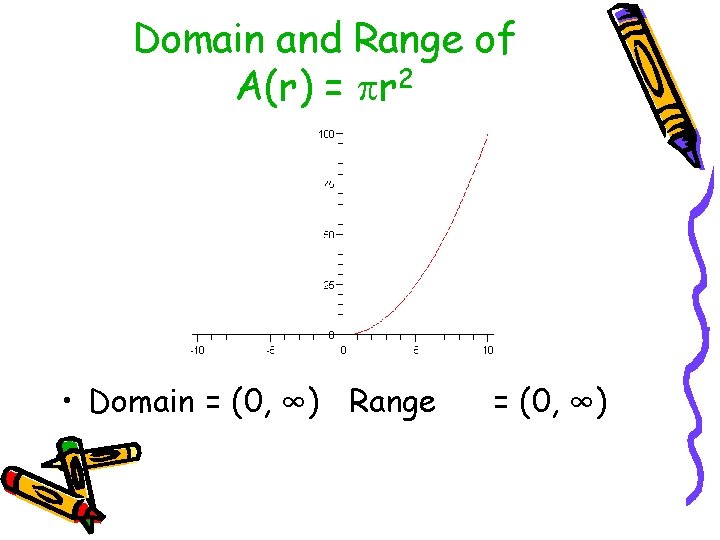
Domain and Range of A(r) = r 2 • Domain = (0, ∞) Range = (0, ∞)

Just a thought… • Mathematical models that describe real-world phenomenon must be as accurate as possible. • We use models to understand the phenomenon and perhaps to make a predictions about future behavior. • A good model simplifies reality enough to permit mathematical calculations but is accurate enough to provide valuable conclusions. • Remember, models have limitations. In the end, Mother Nature has the final say.