DREAM IDEA PLAN IMPLEMENTATION 1 2 Introduction to






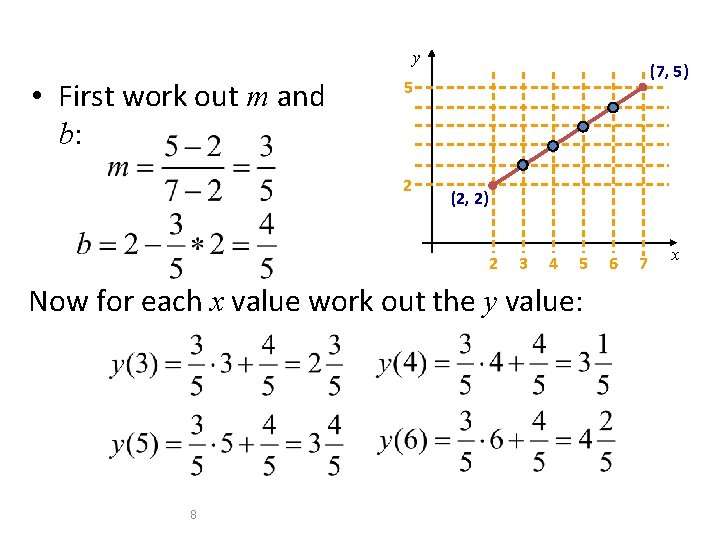

























- Slides: 81

DREAM IDEA PLAN IMPLEMENTATION 1

2

Introduction to Computer Graphics Present to: Amirkabir University of Technology (Tehran Polytechnic) & Semnan University Dr. Kourosh Kiani Email: kkiani 2004@yahoo. com Email: Kourosh. kiani@aut. ac. com Web: aut. ac. com 3

Amirkabir & Semnan University Computer & Electrical Faculty Lecture 05 Scan Conversion Of Line and Circle 4

Rasterization or Scan Conversion is required in order to convert vector data to Raster format 5

2 D basics • Raster - set of horizontal scan lines on a display • Scan line - row of individual pixels • Pixel - picture element; smallest directly addressable element in a raster • Scan Conversion - determining which pixels to set, and with what values 6

5 4 3 2 1 0 0 7 1 2 3 4 5 6 7
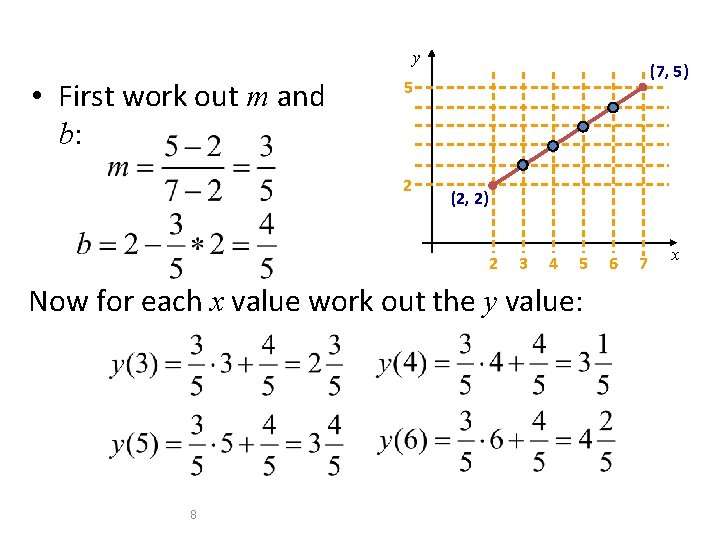
y • First work out m and b: (7, 5) 5 2 (2, 2) 2 3 4 5 Now for each x value work out the y value: 8 6 7 x

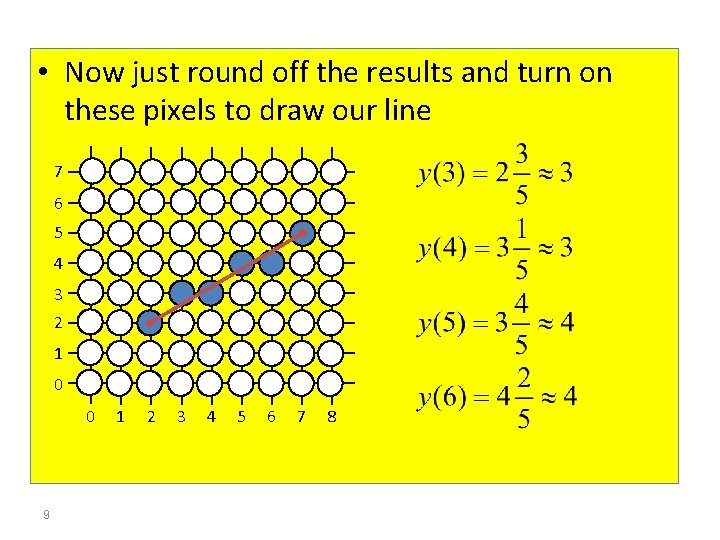
• Now just round off the results and turn on these pixels to draw our line 7 6 5 4 3 2 1 0 0 9 1 2 3 4 5 6 7 8

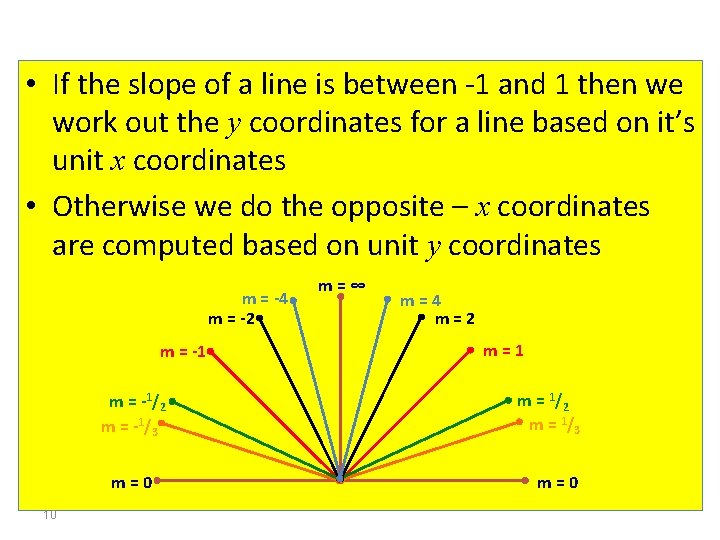
• If the slope of a line is between -1 and 1 then we work out the y coordinates for a line based on it’s unit x coordinates • Otherwise we do the opposite – x coordinates are computed based on unit y coordinates m = -4 m = -2 m = -1/2 m = -1/3 m=0 10 m=∞ m=4 m=2 m=1 m = 1/2 m = 1/3 m=0

Displays – Pixels 11

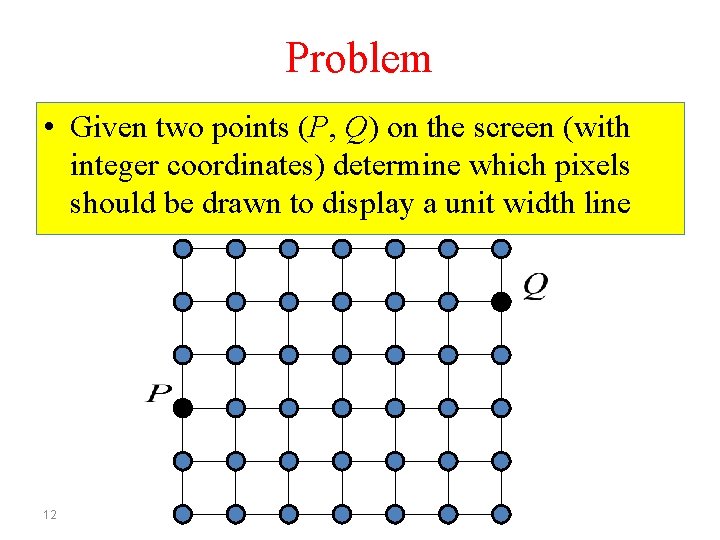
Problem • Given two points (P, Q) on the screen (with integer coordinates) determine which pixels should be drawn to display a unit width line 12

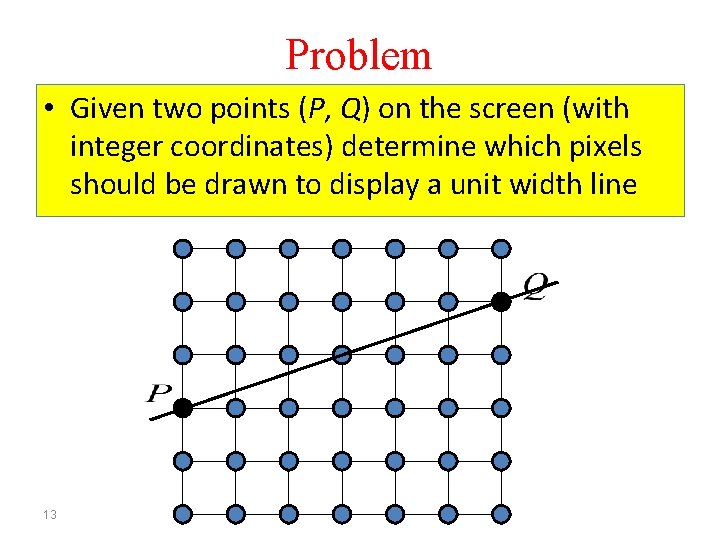
Problem • Given two points (P, Q) on the screen (with integer coordinates) determine which pixels should be drawn to display a unit width line 13

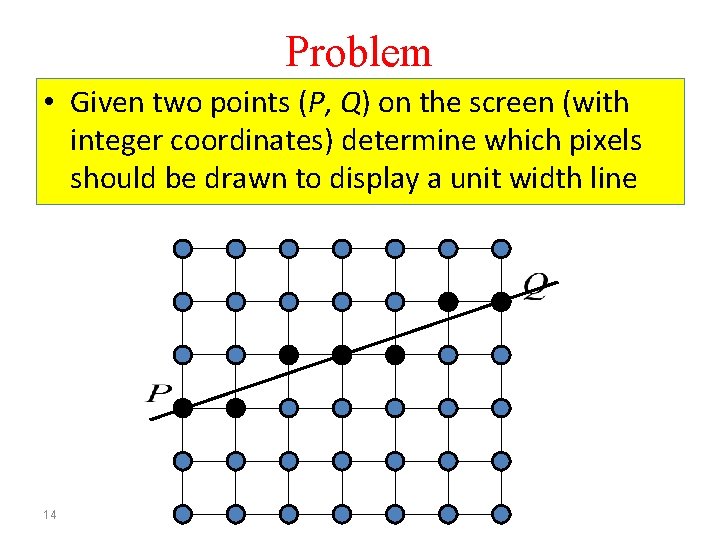
Problem • Given two points (P, Q) on the screen (with integer coordinates) determine which pixels should be drawn to display a unit width line 14

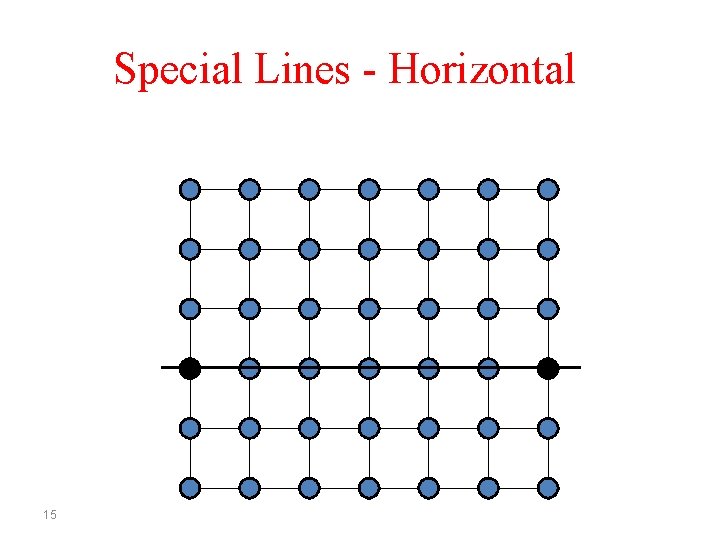
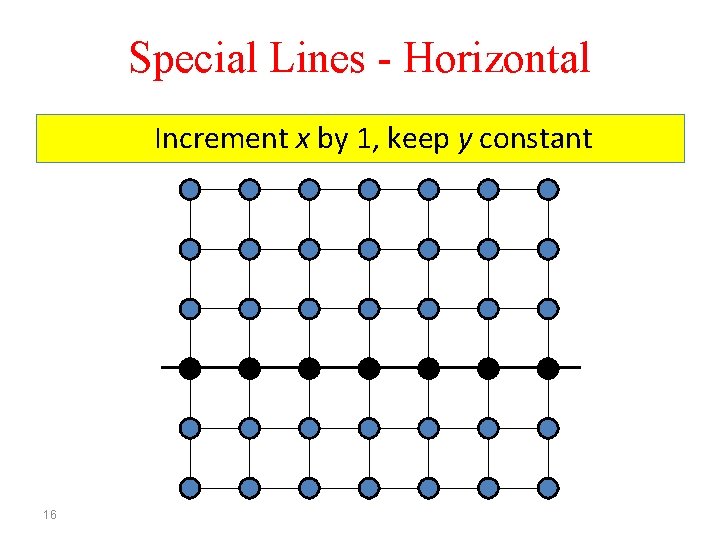
Special Lines - Horizontal 15

Special Lines - Horizontal Increment x by 1, keep y constant 16

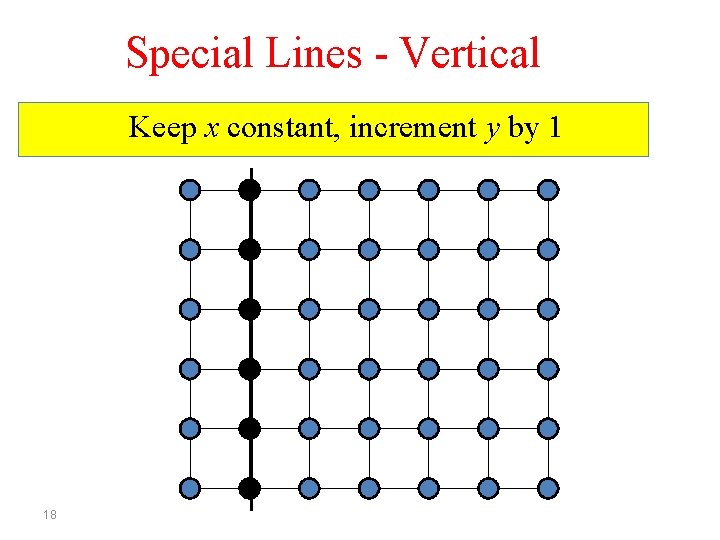
Special Lines - Vertical 17

Special Lines - Vertical Keep x constant, increment y by 1 18

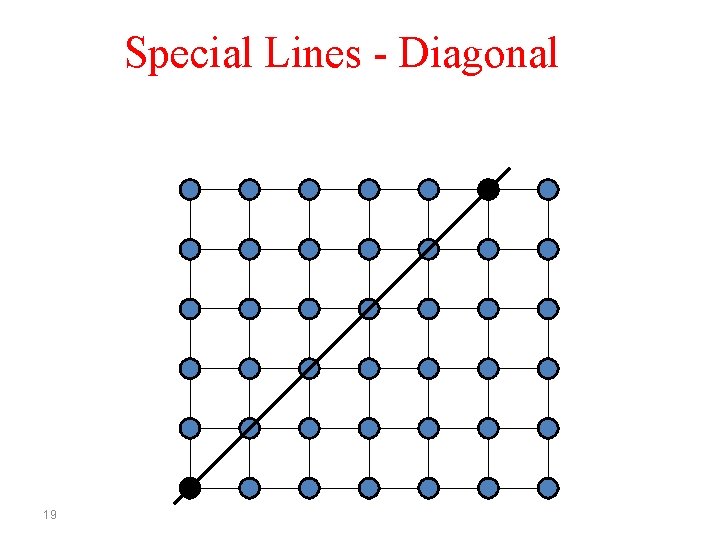
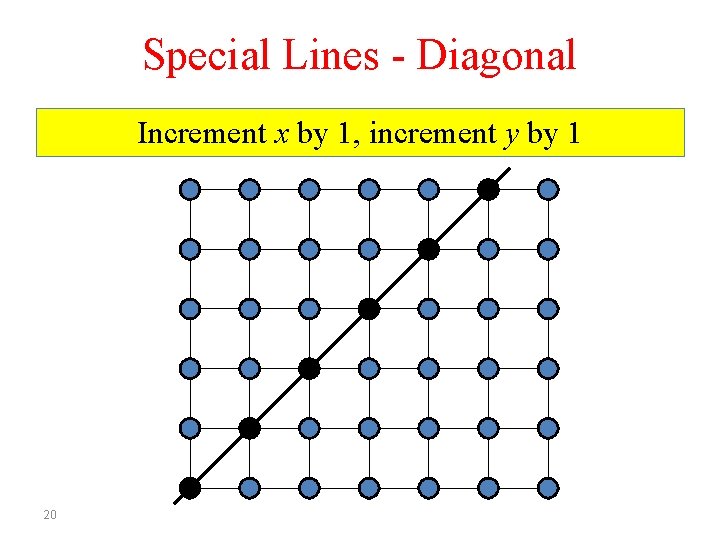
Special Lines - Diagonal 19

Special Lines - Diagonal Increment x by 1, increment y by 1 20

Scan conversion 21

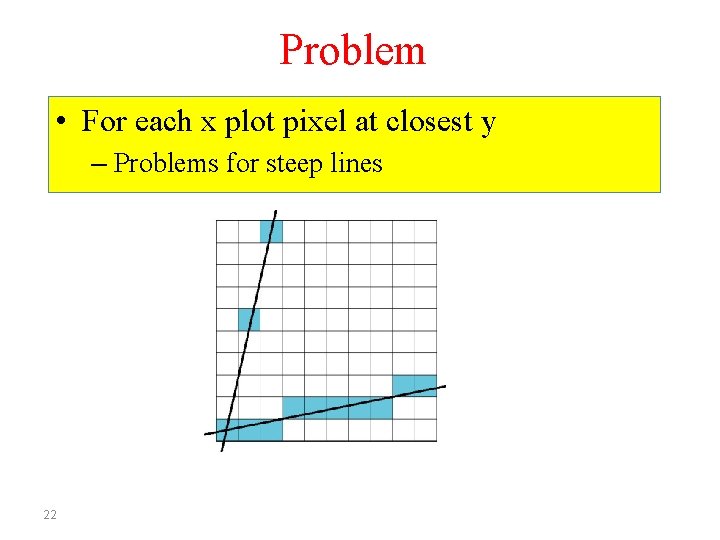
Problem • For each x plot pixel at closest y – Problems for steep lines 22

Using Symmetry • Use for 1 m 0 • For m > 1, swap role of x and y – For each y, plot closest x 23

Arbitrary Lines • Assume • Other lines by swapping x, y or negating • Take steps in x and determine where to fill y 24

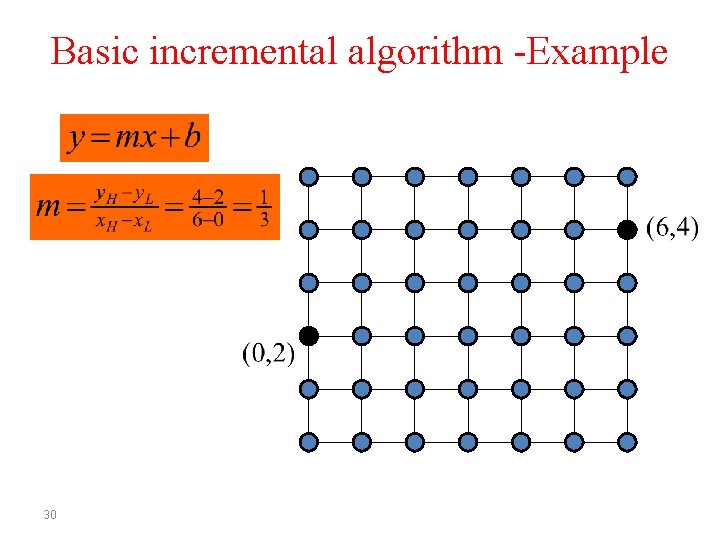
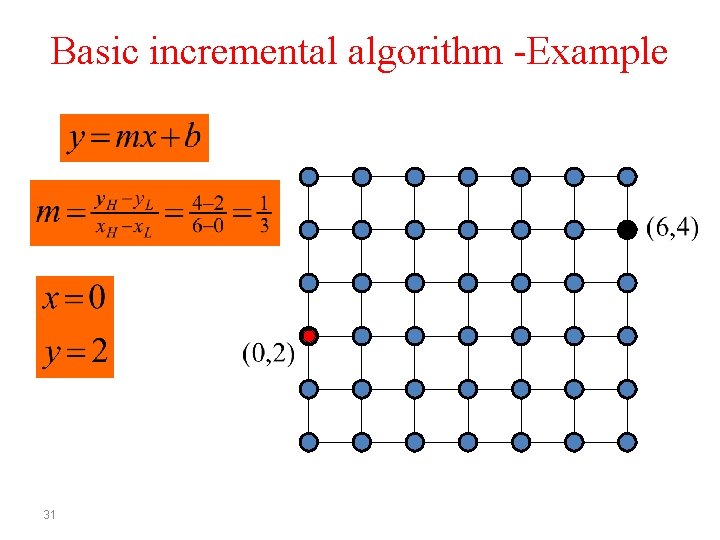
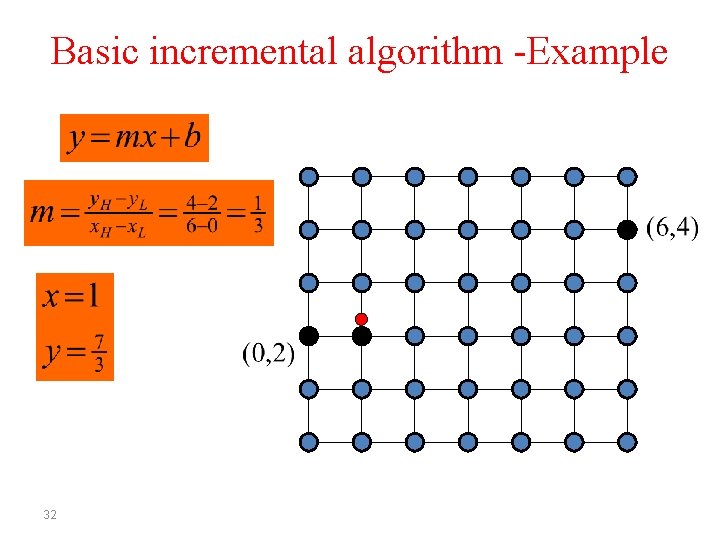
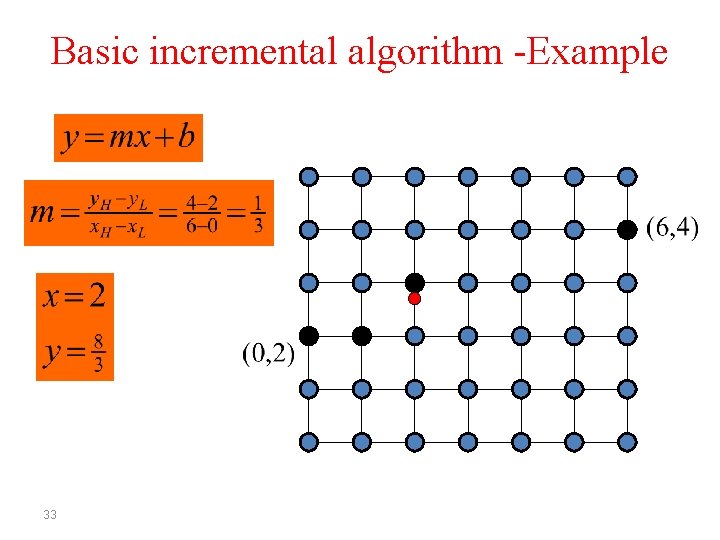
Basic incremental algorithm • Start from (x. L, y. L) and draw to (x. H, y. H) where x. L< x. H ( x 0 , y 0 ) = ( x. L , y L ) For ( i = 0; i <= x. H-x. L; i++ ) Draw. Pixel ( xi, Round ( yi ) ) xi+1 = xi + 1 yi+1 = m xi+1 + b 25

Basic incremental algorithm • Start from (x. L, y. L) and draw to (x. H, y. H) where x. L< x. H ( x 0, y 0 ) = ( x L , y L ) For ( i = 0; i <= x. H-x. L; i++ ) Draw. Pixel ( xi, Round ( yi ) ) xi+1 = xi + 1 yi+1 = m ( xi + 1 ) + b 26

Basic incremental algorithm • Start from (x. L, y. L) and draw to (x. H, y. H) where x. L< x. H ( x 0 , y 0 ) = ( x. L , y L ) For ( i = 0; i <= x. H-x. L; i++ ) Draw. Pixel ( xi, Round ( yi ) ) xi+1 = xi + 1 yi+1 = m xi + m + b 27

Basic incremental algorithm • Start from (x. L, y. L) and draw to (x. H, y. H) where x. L< x. H ( x 0 , y 0 ) = ( x. L , y L ) For ( i = 0; i <= x. H-x. L; i++ ) Draw. Pixel ( xi, Round ( yi ) ) xi+1 = xi + 1 yi+1 = yi + m 28

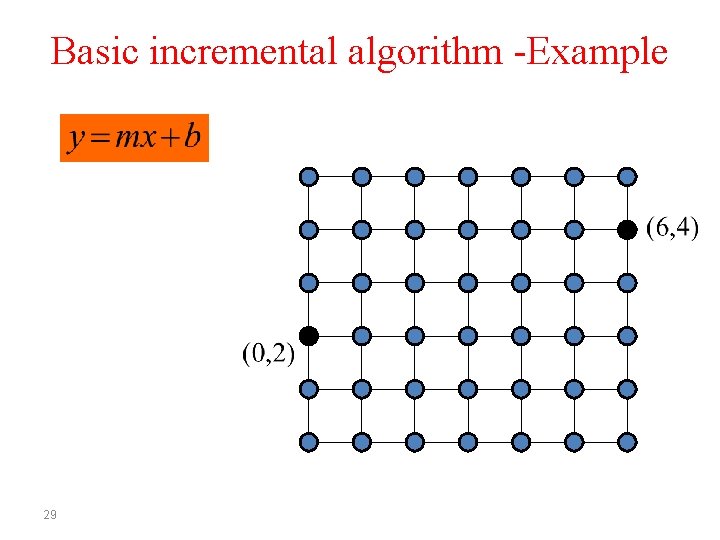
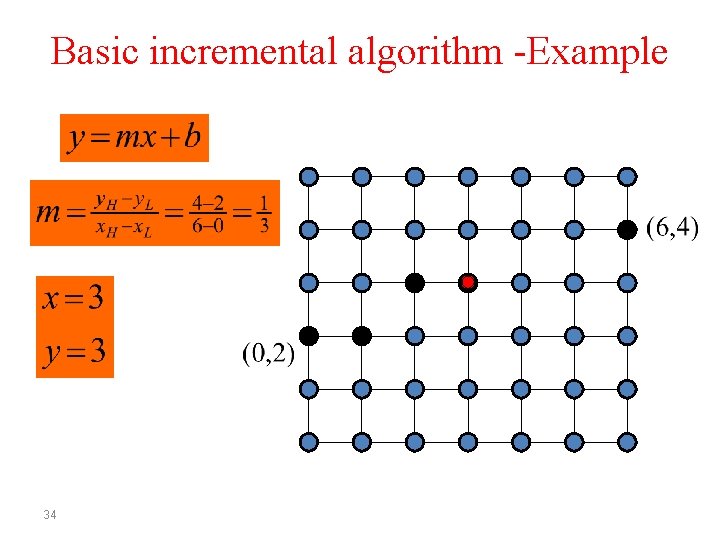
Basic incremental algorithm -Example 29

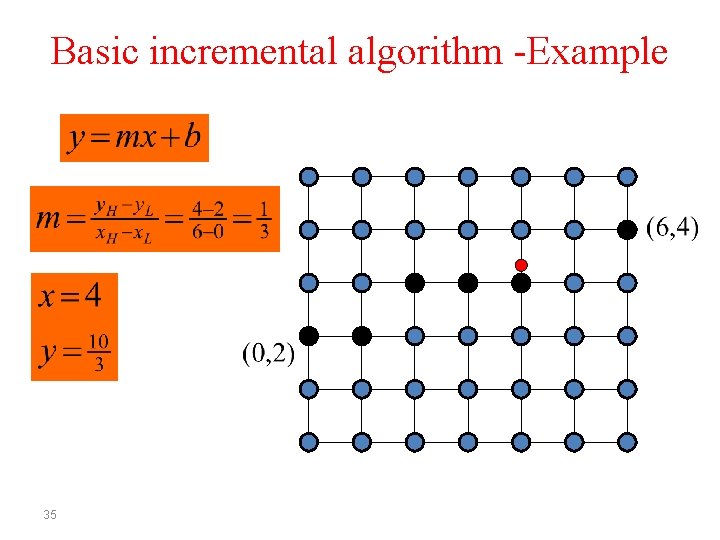
Basic incremental algorithm -Example 30

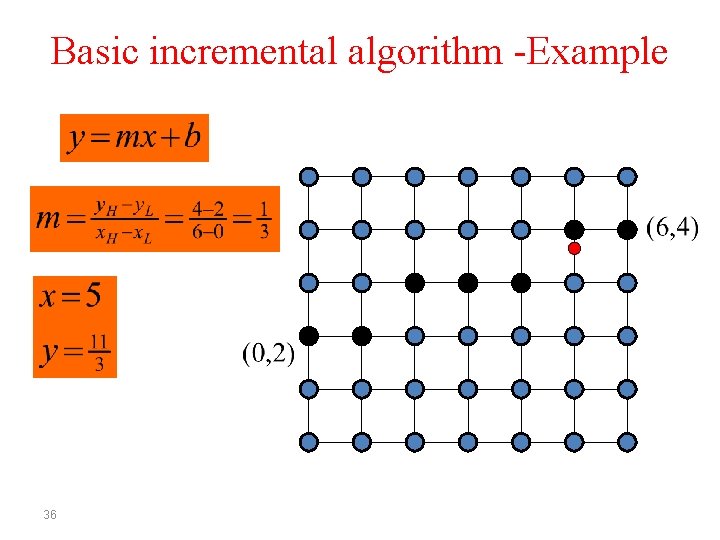
Basic incremental algorithm -Example 31

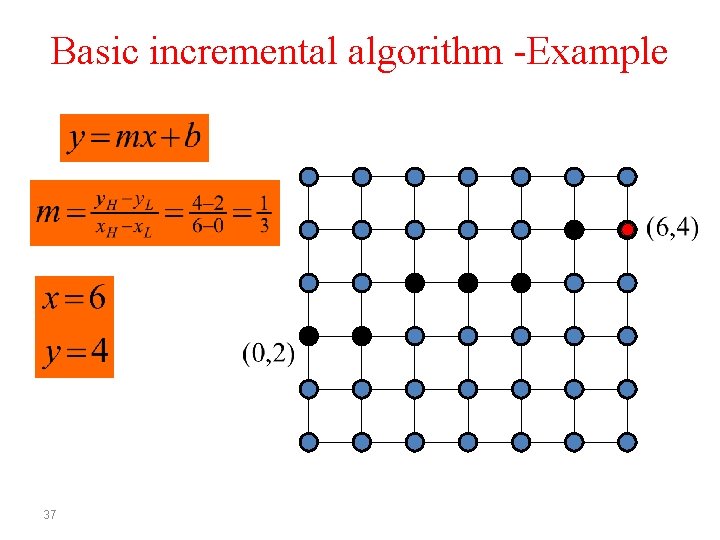
Basic incremental algorithm -Example 32

Basic incremental algorithm -Example 33

Basic incremental algorithm -Example 34

Basic incremental algorithm -Example 35

Basic incremental algorithm -Example 36

Basic incremental algorithm -Example 37

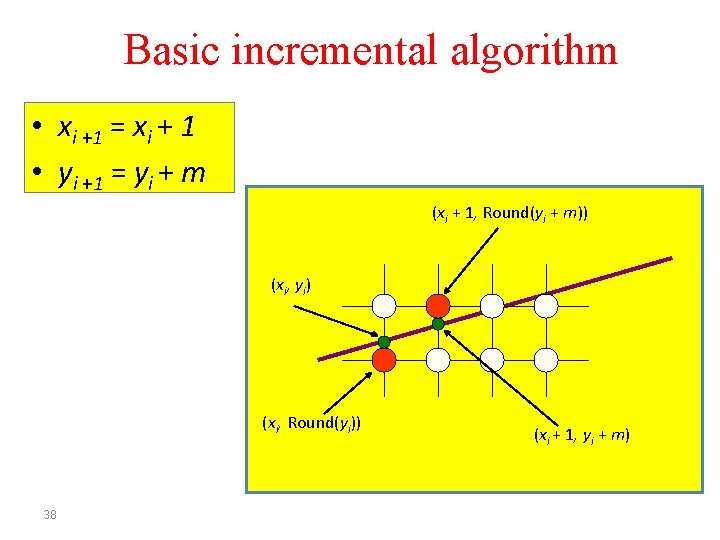
Basic incremental algorithm • xi +1 = xi + 1 • yi +1 = yi + m (xi + 1, Round(yi + m)) ( xi , y i ) (xi, Round(yi)) 38 ( x i + 1 , y i + m)

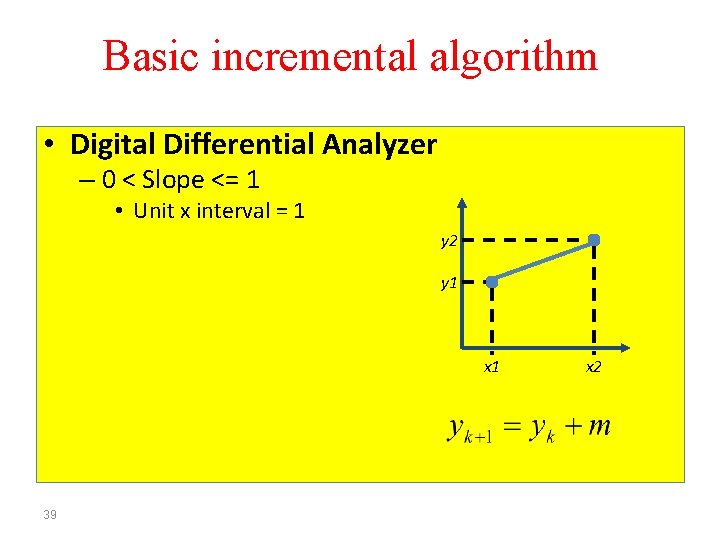
Basic incremental algorithm • Digital Differential Analyzer – 0 < Slope <= 1 • Unit x interval = 1 y 2 y 1 x 1 39 x 2

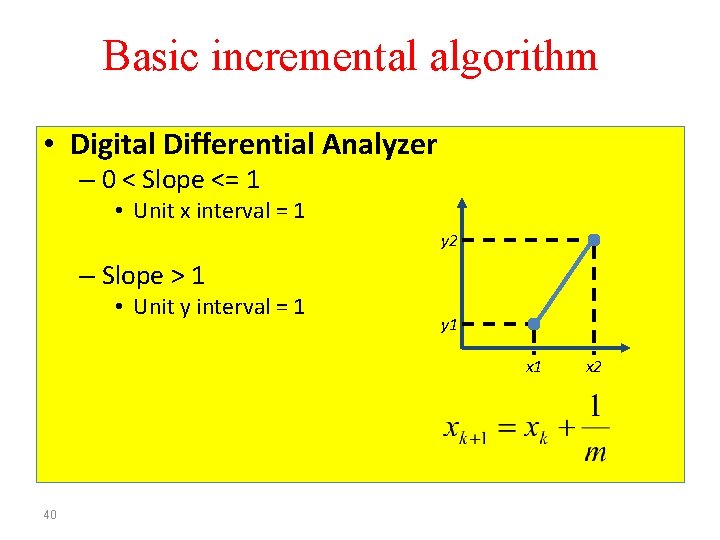
Basic incremental algorithm • Digital Differential Analyzer – 0 < Slope <= 1 • Unit x interval = 1 y 2 – Slope > 1 • Unit y interval = 1 y 1 x 1 40 x 2

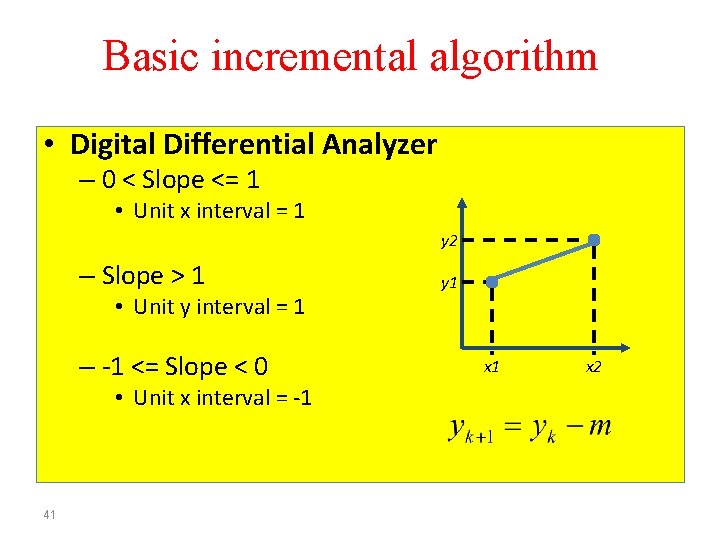
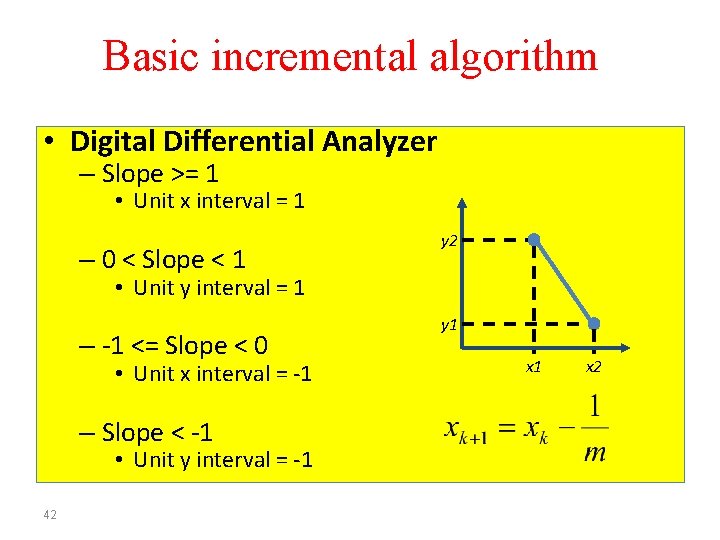
Basic incremental algorithm • Digital Differential Analyzer – 0 < Slope <= 1 • Unit x interval = 1 y 2 – Slope > 1 • Unit y interval = 1 – -1 <= Slope < 0 • Unit x interval = -1 41 y 1 x 2

Basic incremental algorithm • Digital Differential Analyzer – Slope >= 1 • Unit x interval = 1 – 0 < Slope < 1 y 2 • Unit y interval = 1 – -1 <= Slope < 0 • Unit x interval = -1 – Slope < -1 • Unit y interval = -1 42 y 1 x 2

Basic incremental algorithm -Problems • Floating point operations • Rounding • Can we do better? ( x 0, y 0 ) = ( x L , y L ) For ( i = 0; i <= x. H-x. L; i++ ) Draw. Pixel ( xi, Round ( yi ) ) xi+1 = xi + 1 yi+1 = yi + m 43

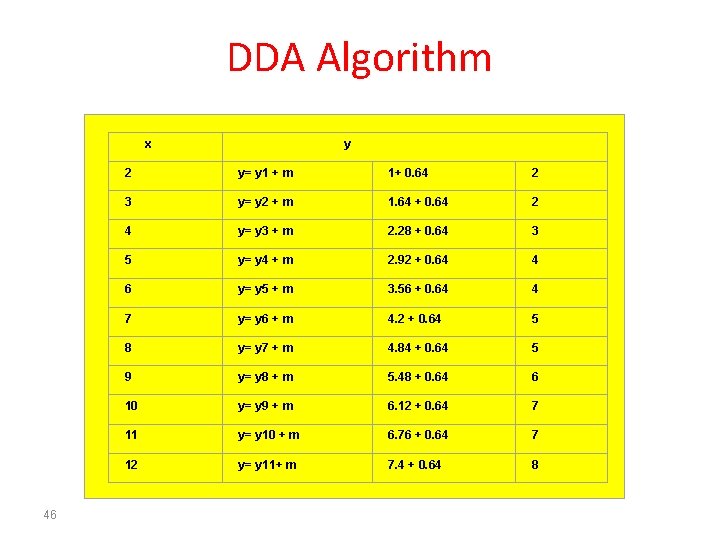
Basic incremental algorithm DDA Sample line at unit intervals on one axis and calculate the corresponding co-ordinate on the other axis. E. g. Line from (1, 1) to (12, 8) x 1 = 1 and y 1 =1 x 2 =12 and y 2 = 8 Algorithm (for slope 0 < m < 1) y = 8 – 1 = 7 x = 12 – 1 = 11 m = y / x = 7/11 = 0. 64 Plot the first point (1, 1) For each x co-ordinate between x= 2 and x= 12 y co-ordinate = previous y co-ordinate + m plot point at (x, y) 44

C Implementation of DDA # define ROUND (a) ((int) (a+0. 5)) void plot_point(int x, int y); void line_DDA(int x 1, int y 1, int x 2, int y 2) { int dx, dy, steps, k; float x_increment, y_increment, x, y; if (abs(dx) > abs(dy)) steps = abs(dx); else steps = abs(dy); x_increment = dx / (float) steps; y_increment = dy / (float) steps; plot_point(ROUND(x), ROUND(y)); for (k=0; k< steps; k ++) x += x_increment; y +=y_increment; plot_point(ROUND(x), ROUND(y)); 45 }

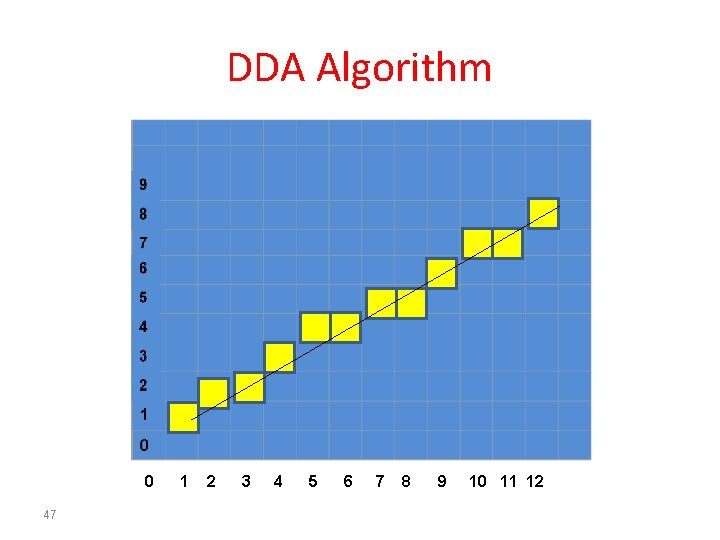
DDA Algorithm x 46 y 2 y= y 1 + m 1+ 0. 64 2 3 y= y 2 + m 1. 64 + 0. 64 2 4 y= y 3 + m 2. 28 + 0. 64 3 5 y= y 4 + m 2. 92 + 0. 64 4 6 y= y 5 + m 3. 56 + 0. 64 4 7 y= y 6 + m 4. 2 + 0. 64 5 8 y= y 7 + m 4. 84 + 0. 64 5 9 y= y 8 + m 5. 48 + 0. 64 6 10 y= y 9 + m 6. 12 + 0. 64 7 11 y= y 10 + m 6. 76 + 0. 64 7 12 y= y 11+ m 7. 4 + 0. 64 8

DDA Algorithm 0 47 1 2 3 4 5 6 7 8 9 10 11 12

DDA Algorithm • DDA (“Digital Differential Analyzer”) • Assume 0 m 1 else flip about y= x line. (xi, Round(yi+m)) Desired Line (xi, yi) (xi, Round(yi)) (xi, yi +m) void Line(int x 0, int y 0, int x 1, int y 1, int value) { double y = y 0; double m = (y 1 – y 0) / (x 0 – x 1); // 0 <= m <= 1 for (int x = x 0; x <= x 1; x++) { Write. Pixel(x, Round(y), value); y += m; } Require to eliminate floating point operations & variables }48

Midpoint line algorithm • Basic incremental algorithm uses real coordinates and floating-point operations Round( ) • Midpoint use integers and integer operations • First published by Pitteway (1967); later adapted by Van Aken (1984), Bresenham, and others 49

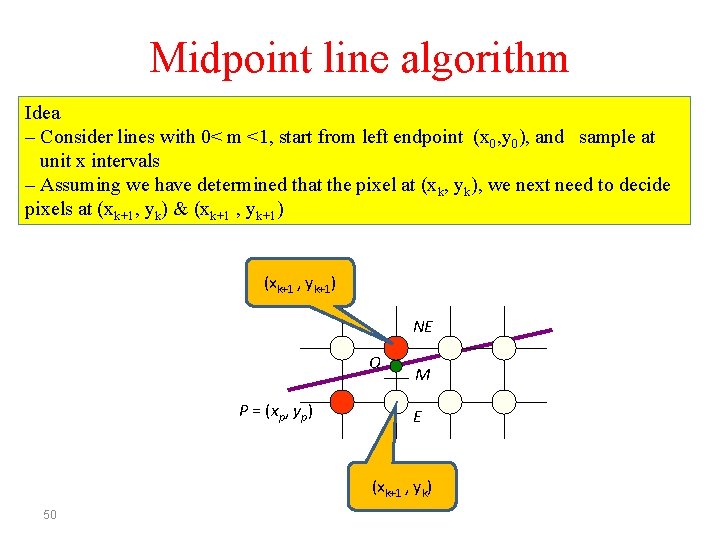
Midpoint line algorithm Idea – Consider lines with 0< m <1, start from left endpoint (x 0, y 0), and sample at unit x intervals – Assuming we have determined that the pixel at (xk, yk), we next need to decide pixels at (xk+1, yk) & (xk+1 , yk+1) NE Q P = (xp, yp) M E (xk+1 , yk) 50

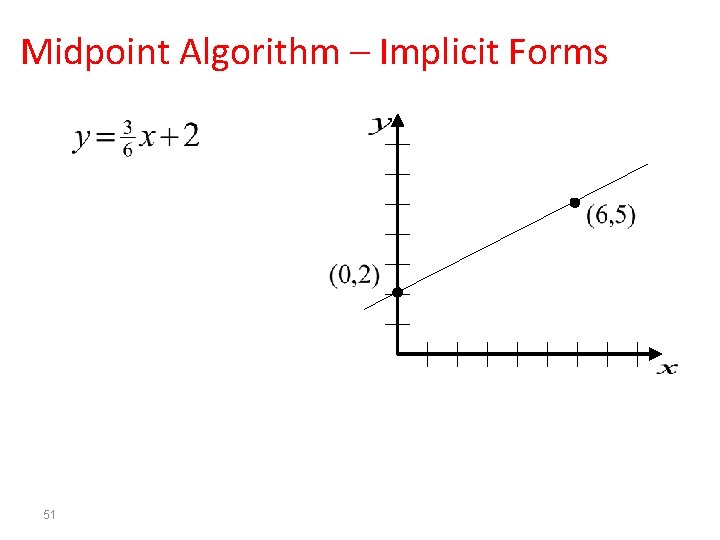
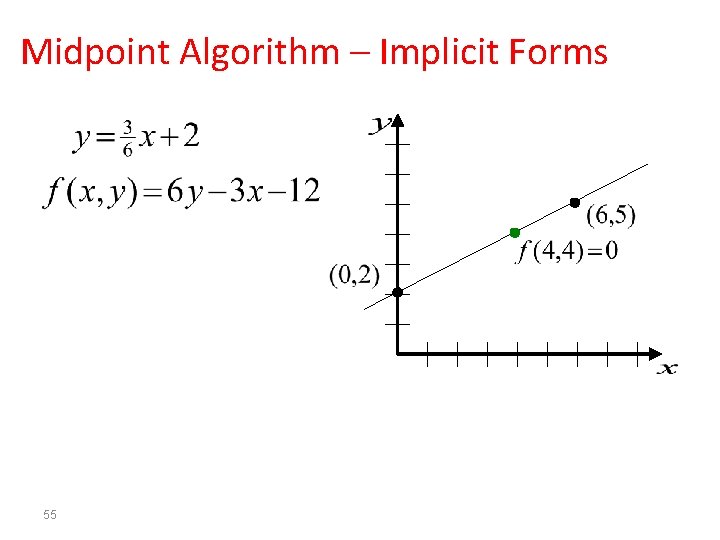
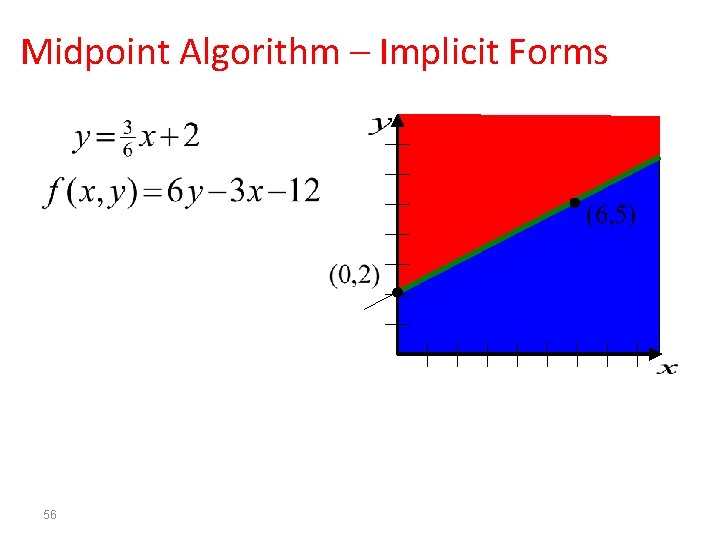
Midpoint Algorithm – Implicit Forms 51

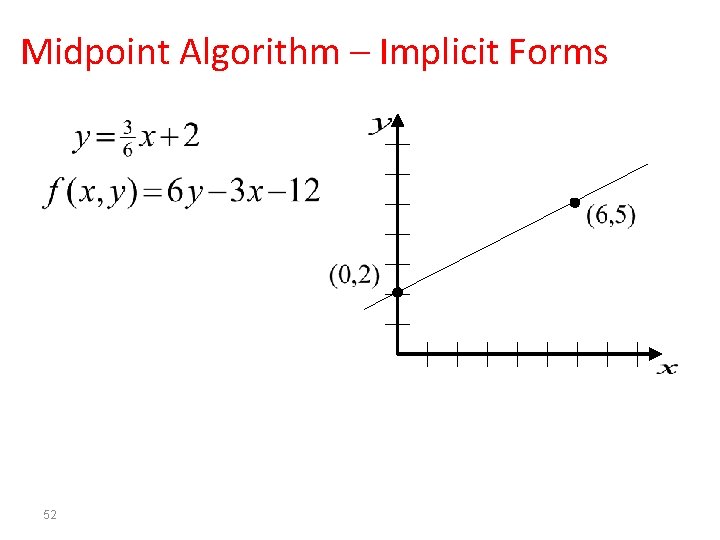
Midpoint Algorithm – Implicit Forms 52

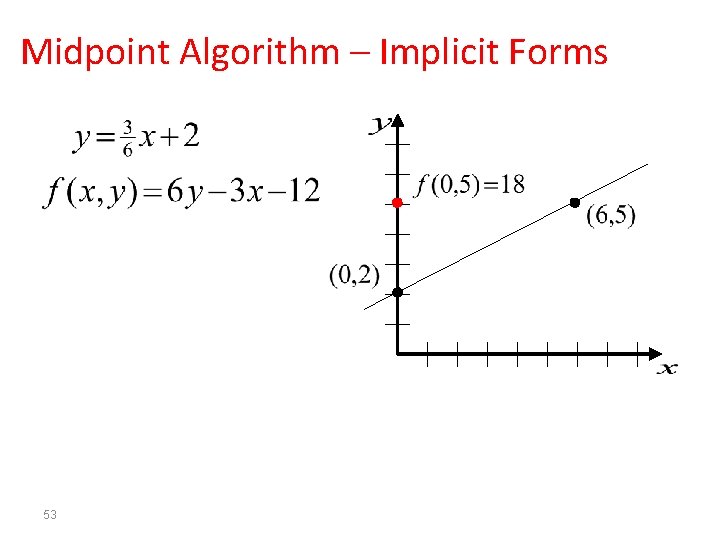
Midpoint Algorithm – Implicit Forms 53

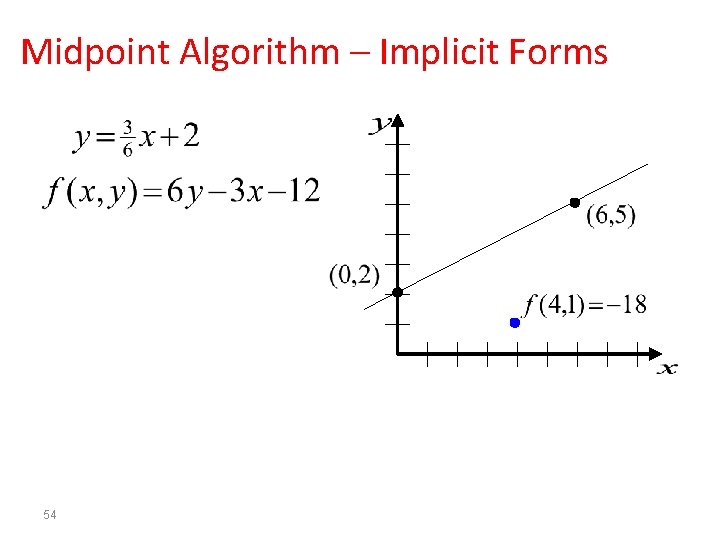
Midpoint Algorithm – Implicit Forms 54

Midpoint Algorithm – Implicit Forms 55

Midpoint Algorithm – Implicit Forms 56

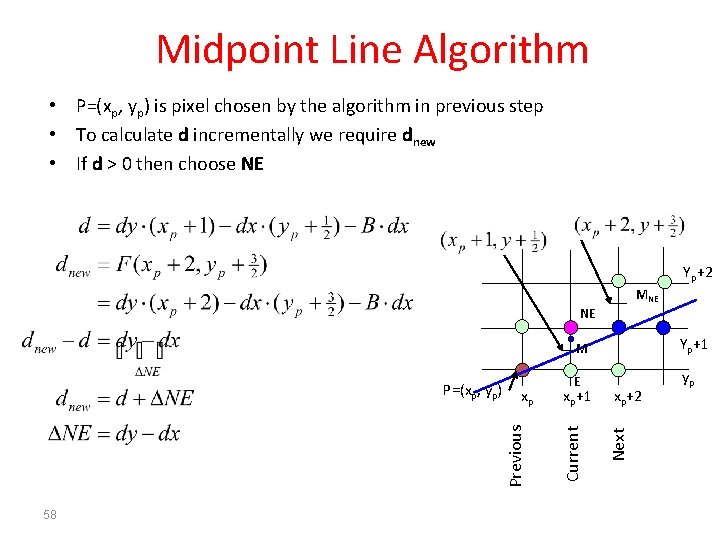
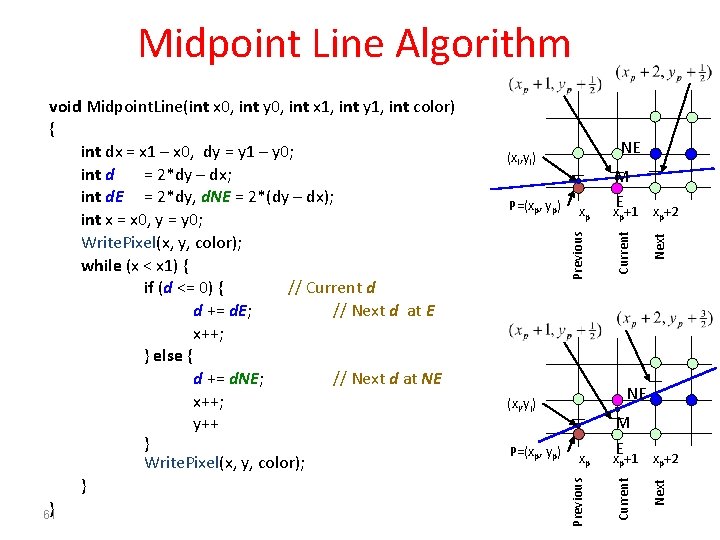
Midpoint Line Algorithm • Assume – 0 m 1 [ else flip about y= x line. ] – (x 0, y 0) and (x 1, y 1) are integer values • At each iteration we determine if the line intersects the next pixel above or below its midpoint y value. – if above then NE ynew = yp+1 – otherwise E ynew = yp d=F(M) > 0 NE P=(xp, yp) xp d=F(M) < 0 E P=(xp, yp) 57 xp N ME yp+1 Ex +1 yp p p

Midpoint Line Algorithm • P=(xp, yp) is pixel chosen by the algorithm in previous step • To calculate d incrementally we require dnew • If d > 0 then choose NE Yp+2 MNE NE 58 Yp+1 E yp xp+2 Next xp+1 Current xp Previous P=(xp, yp) M

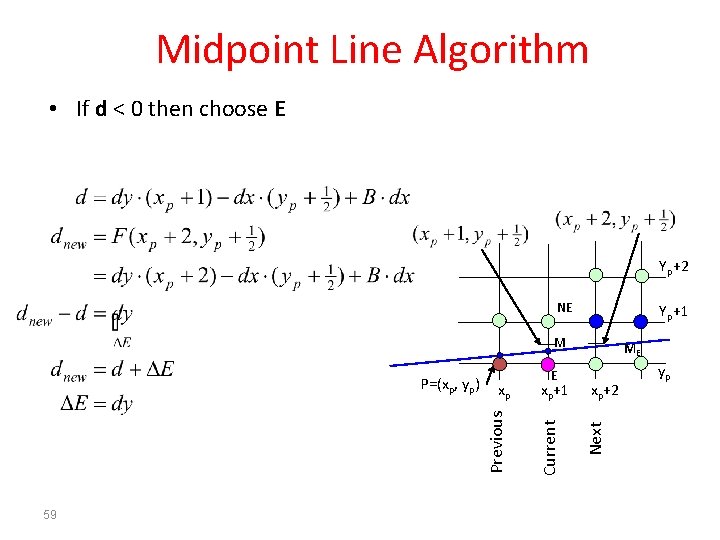
Midpoint Line Algorithm • If d < 0 then choose E Yp+2 NE Yp+1 M 59 xp+1 xp+2 Next E Current xp Previous P=(xp, yp) ME yp

Midpoint Line Algorithm • To find Initial value of d NE M Multiply by 2 to avoid fractions. Redefine d 0, E, NE n 60 x 0+1 Initial do Only fractional value E Start P=(x 0, y 0)

Midpoint Line Algorithm NE xp+2 NE p xp+2 Next xp M E x +1 Current (xi, yi) P=(xp, yp) p Next xp Previous P=(xp, yp) M E x +1 Current (xi, yi) Previous void Midpoint. Line(int x 0, int y 0, int x 1, int y 1, int color) { int dx = x 1 – x 0, dy = y 1 – y 0; int d = 2*dy – dx; int d. E = 2*dy, d. NE = 2*(dy – dx); int x = x 0, y = y 0; Write. Pixel(x, y, color); while (x < x 1) { if (d <= 0) { // Current d d += d. E; // Next d at E x++; } else { d += d. NE; // Next d at NE x++; y++ } Write. Pixel(x, y, color); } } 61

Midpoint line algorithm • Questions… Does this work for all slopes? Does this work for all directions? • Okay, break into groups and talk about it! 62

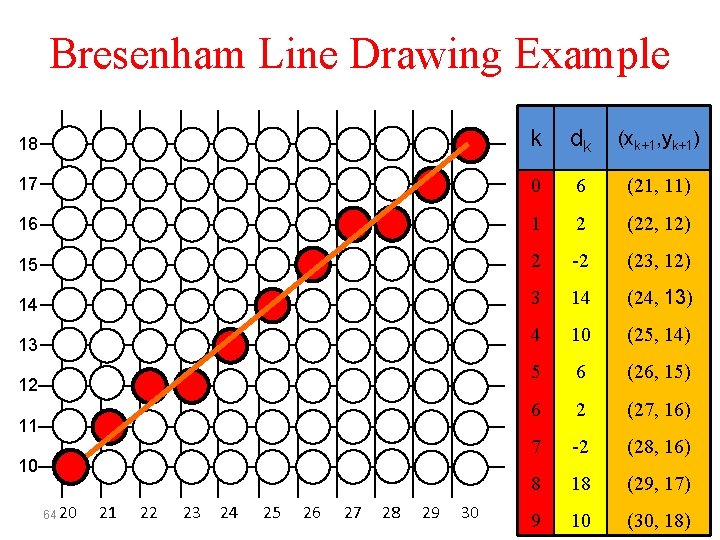
Bresenham Line Drawing Example • To illustrate the algorithm, we digitize the line with endpoints (20, 10) and (30, 18). This line has a slope of 0. 8 with dx = 10, dy = 8, d =2 dy-dx =6, d. E =dy = 16, d. NE=2 dy-2 dx=-4 (x 0, y 0) = (20, 10) 63

Bresenham Line Drawing Example 18 k dk (xk+1, yk+1) 17 0 6 (21, 11) 16 1 2 (22, 12) 15 2 -2 (23, 12) 14 3 14 (24, 13) 4 10 (25, 14) 5 6 (26, 15) 6 2 (27, 16) 7 -2 (28, 16) 8 18 (29, 17) 9 10 (30, 18) 13 12 11 10 64 20 21 22 23 24 25 26 27 28 29 30

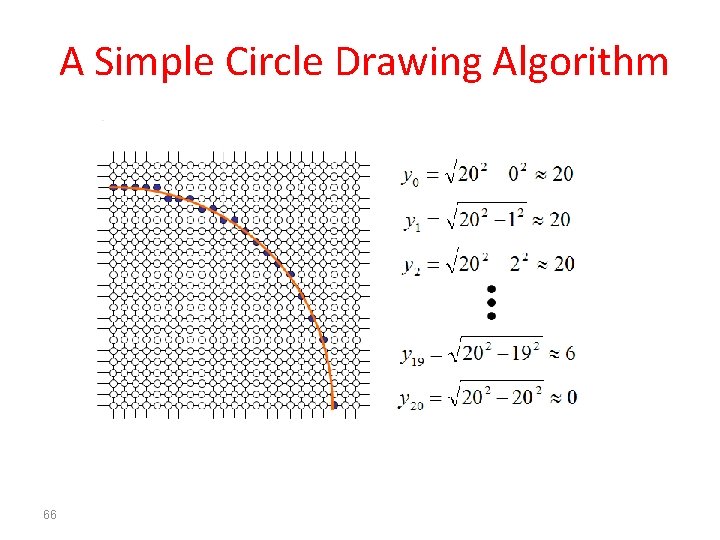
A Simple Circle Drawing Algorithm • The equation for a circle is: • where r is the radius of the circle • So, we can write a simple circle drawing algorithm by solving the equation for y at unit x intervals using: 65

A Simple Circle Drawing Algorithm 66

A Simple Circle Drawing Algorithm (cont…) • However, unsurprisingly this is not a brilliant solution! • Firstly, the resulting circle has large gaps where the slope approaches the vertical • Secondly, the calculations are not very efficient – The square (multiply) operations – The square root operation – try really hard to avoid these! • We need a more efficient, more accurate solution 67

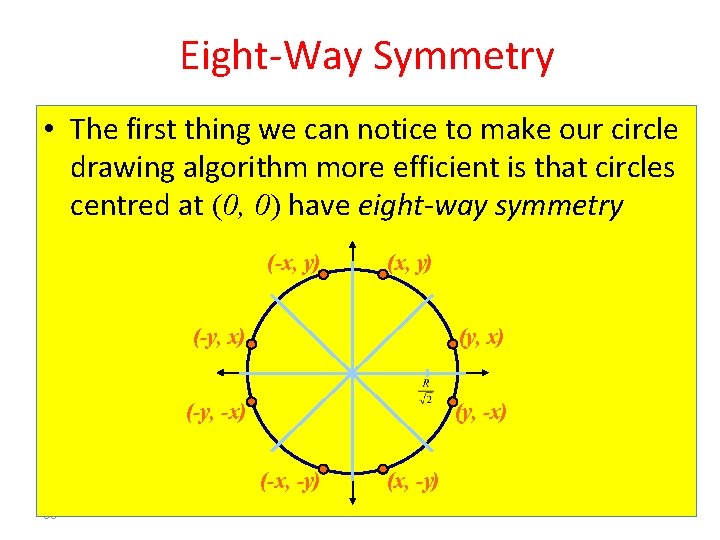
Eight-Way Symmetry • The first thing we can notice to make our circle drawing algorithm more efficient is that circles centred at (0, 0) have eight-way symmetry (-x, y) (-y, x) (-y, -x) (-x, -y) 68 (x, y) (x, -y)

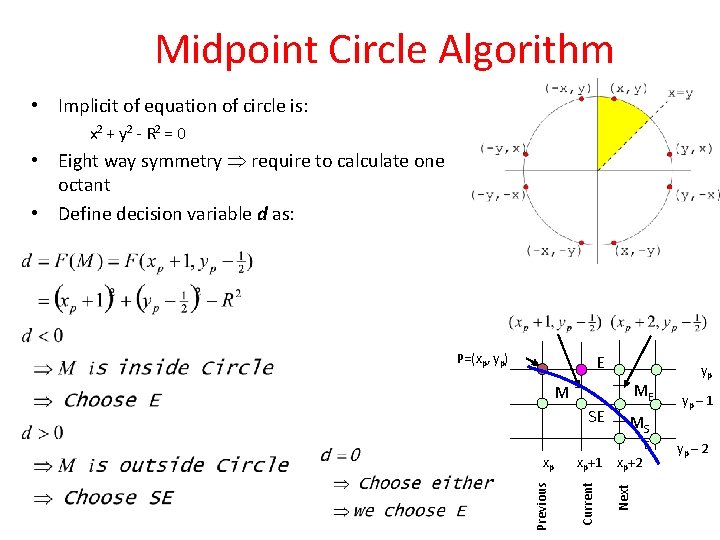
Midpoint Circle Algorithm • Implicit of equation of circle is: x 2 + y 2 - R 2 = 0 • Eight way symmetry require to calculate one octant • Define decision variable d as: P=(xp, yp) E ME M SE xp+1 xp+2 Current Next Previous yp – 1 MS E xp yp yp – 2

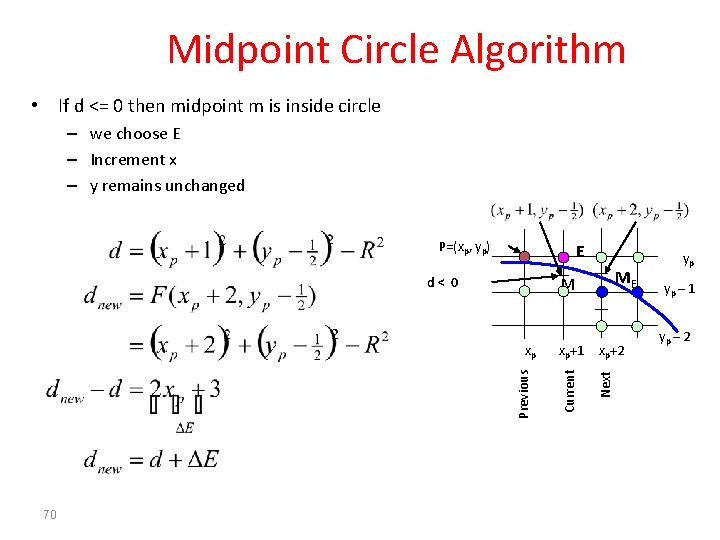
Midpoint Circle Algorithm • If d <= 0 then midpoint m is inside circle – we choose E – Increment x – y remains unchanged P=(xp, yp) E xp+1 xp+2 Current Next Previous xp 70 ME M d< 0 yp yp – 1 yp – 2

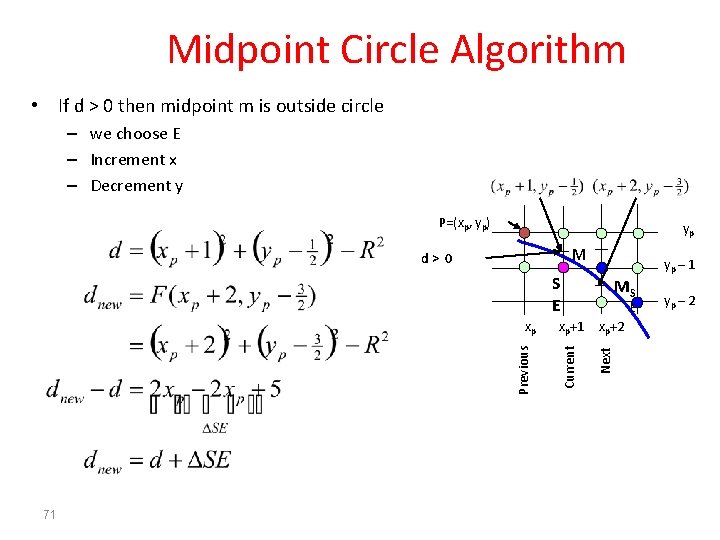
Midpoint Circle Algorithm • If d > 0 then midpoint m is outside circle – we choose E – Increment x – Decrement y P=(xp, yp) yp M d> 0 yp – 1 S E 71 xp+2 Next E Current Previous xp MS yp – 2

Midpoint Circle Algorithm Initial condition • Starting pixel (0, R) • Next Midpoint lies at (1, R – ½) • d 0 = F(1, R – ½) = 1 + (R 2 – R + ¼) – R 2 = 5/4 – R • To remove the fractional value 5/4 : – Consider a new decision variable h as, h = d – ¼ – Substituting d for h + ¼, • d 0=5/4 – R h = 1 – R • d<0 h<–¼ h<0 • Since h starts out with an integer value and is incremented by integer value ( E or SE), we can change the comparison to just h < 0 72

Midpoint Circle Algorithm void Midpoint. Circle(int radius, int value) { int x = 0; int y = radius ; int d = 1 – radius ; Circle. Points(x, y, value); while (y > x) { if (d < 0) { /* Select E */ d += 2 * x + 3; } else { /* Select SE */ d += 2 * ( x – y ) + 5; y – –; } x++; Circle. Points(x, y, value); } } 73

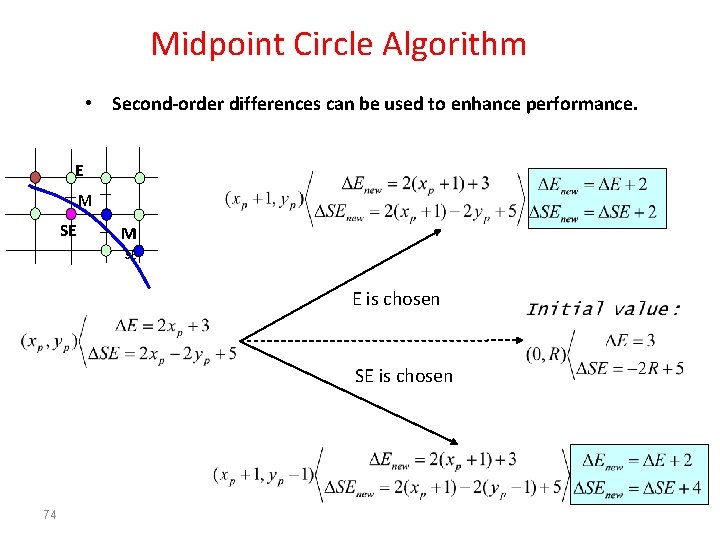
Midpoint Circle Algorithm • Second-order differences can be used to enhance performance. E M SE E is chosen SE is chosen 74

Midpoint Circle Algorithm 75 void Midpoint. Circle(int radius, int value) { int x = 0; int y = radius ; int d = 1 – radius ; int d. E = 3; int d. SE = -2*radius +5; Circle. Points(x, y, value); while (y > x) { if (d < 0) { /* Select E */ d += d. E; d. E += 2; d. SE += 2; } else { d += d. SE; d. E += 2; d. SE += 4; y – –; } x++; Circle. Points(x, y, value); } } /* Select SE */

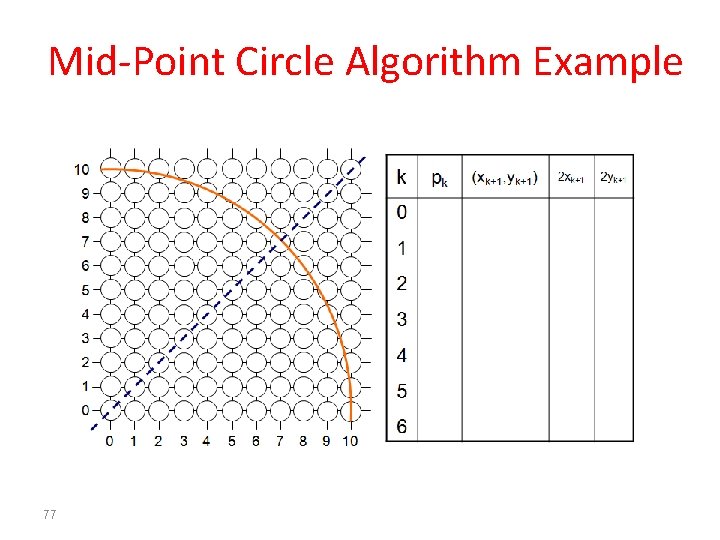
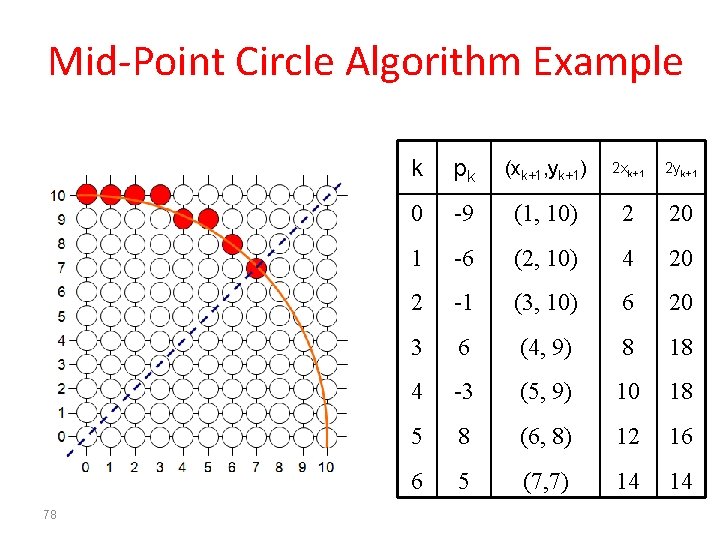
Mid-Point Circle Algorithm Example • To see the mid-point circle algorithm in action lets use it to draw a circle centred at (0, 0) with radius 10 76

Mid-Point Circle Algorithm Example 77

Mid-Point Circle Algorithm Example 78 k pk (xk+1, yk+1) 2 xk+1 2 yk+1 0 -9 (1, 10) 2 20 1 -6 (2, 10) 4 20 2 -1 (3, 10) 6 20 3 6 (4, 9) 8 18 4 -3 (5, 9) 10 18 5 8 (6, 8) 12 16 6 5 (7, 7) 14 14

Mid-Point Circle Algorithm Summary • The key insights in the mid-point circle algorithm are: – Eight-way symmetry can hugely reduce the work in drawing a circle – Moving in unit steps along the x axis at each point along the circle’s edge we need to choose between two possible y coordinates 79

Questions? Discussion? Suggestions ?

81