DREAM IDEA PLAN IMPLEMENTATION 1 2 Introduction to

DREAM IDEA PLAN IMPLEMENTATION 1

2

Introduction to Image Processing Present to: Amirkabir University of Technology (Tehran Polytechnic) & Semnan University Dr. Kourosh Kiani Email: kkiani 2004@yahoo. com Email: Kourosh. kiani@aut. ac. ir Email: Kourosh. kiani@semnan. ac. ir Web: www. kouroshkiani. com 3

Lecture 07 FOURIER SERIES 4

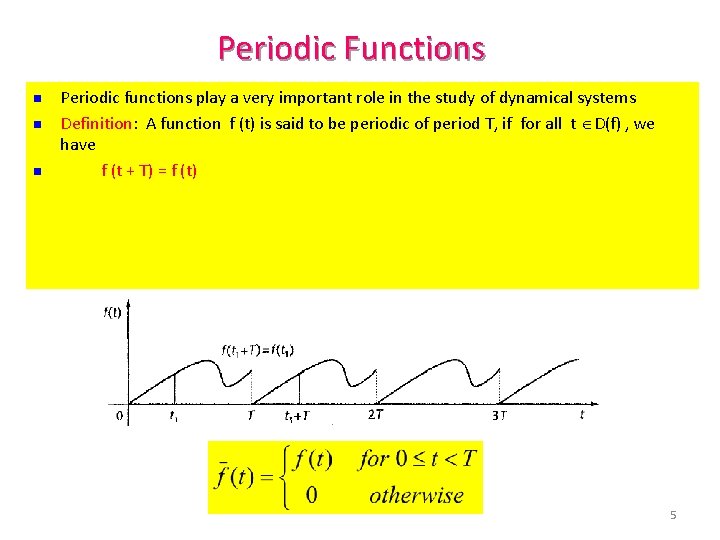
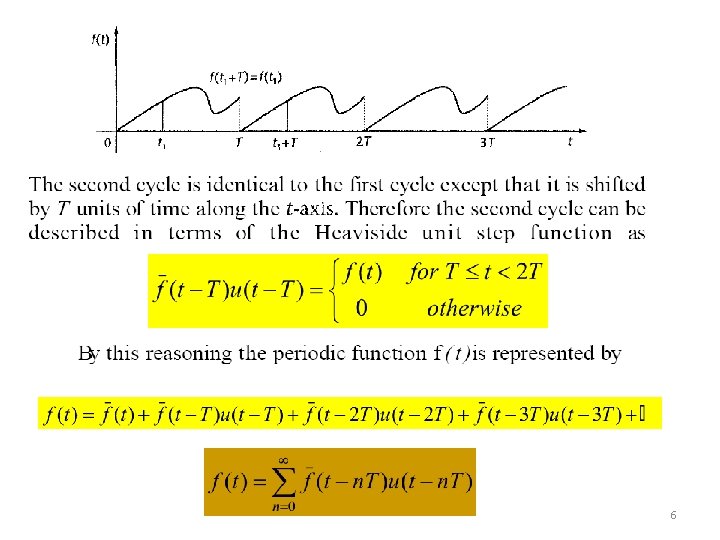
Periodic Functions n n n Periodic functions play a very important role in the study of dynamical systems Definition: A function f (t) is said to be periodic of period T, if for all t D(f) , we have f (t + T) = f (t) 5

6

Periodic Signals n A periodic signal f(t) Unchanged when time-shifted by one period Two-sided: extent is t (- , ) May be generated by periodically extending one period Area under f(t) over any interval of duration equal to the period is the same; e. g. , integrating from 0 to T 0 would give the same value as integrating from –T 0/2 to T 0 /2 7

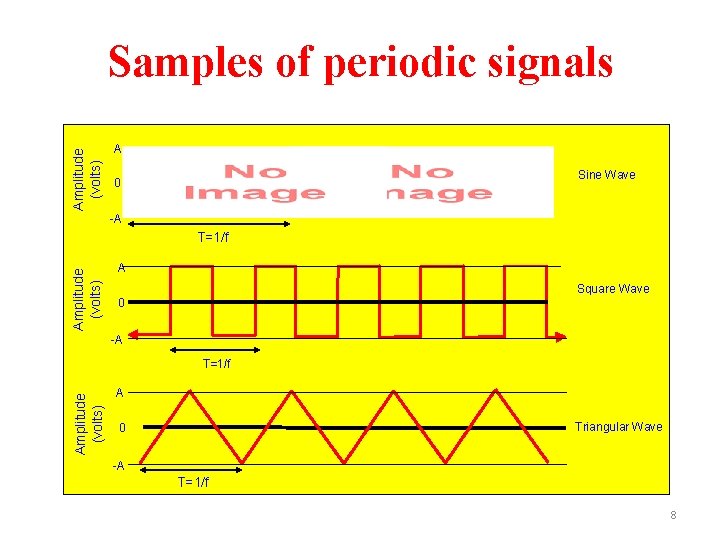
Amplitude (volts) Samples of periodic signals A Sine Wave 0 -A Amplitude (volts) T=1/f A Square Wave 0 -A Amplitude (volts) T=1/f A Triangular Wave 0 -A T=1/f 8

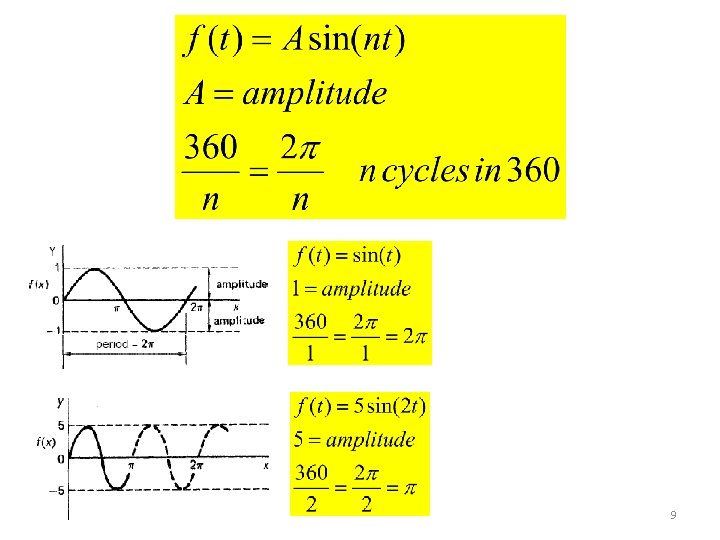
9

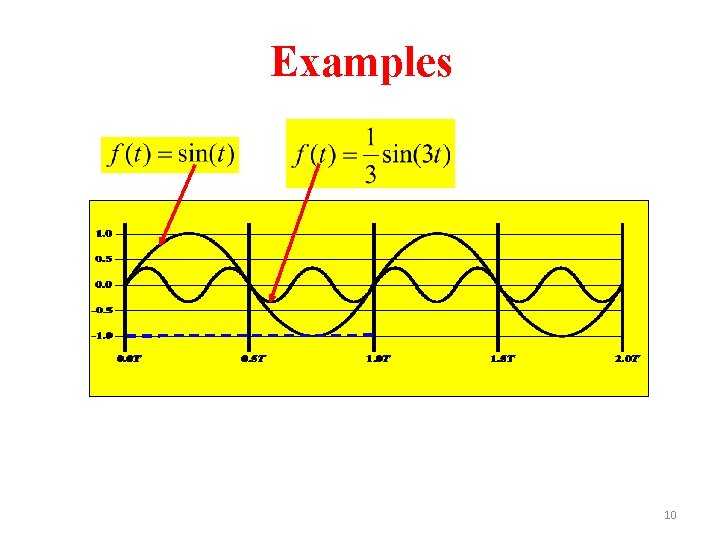
Examples 10

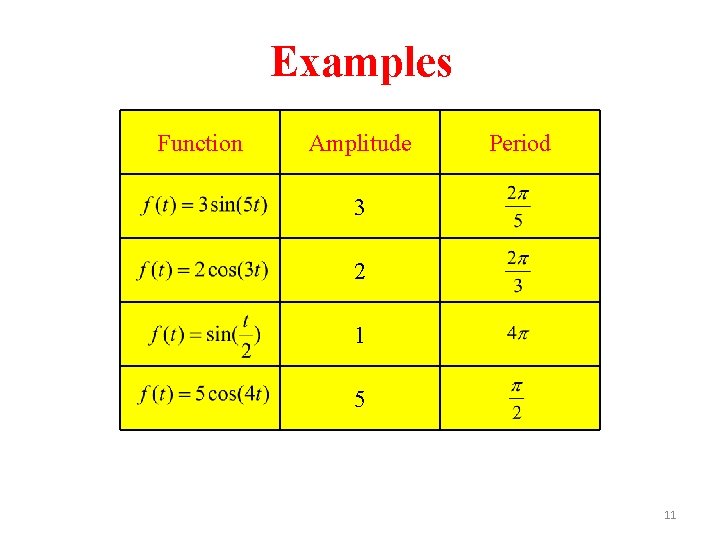
Examples Function Amplitude Period 3 2 1 5 11

Common Period Consider two periodic function f 1(t) and f 2(t) with respectively periods T 1 and T 2. If the ratio T 1/T 2 is a rational number, then T=n 1 T 1=n 2 T 2 is a common period of f 1(t) and f 2(t) If T 1/T 2 is a rational number, the cos(w 1 t) and cos(w 2 t) have a common period. If T 1/T 2 is irrational, they do not have a common period. 12

Example What is period of the function 13

Example What is period of the function The f(t) is not periodic. 14

Example What is period of the function 15

Example What is period of the function 16

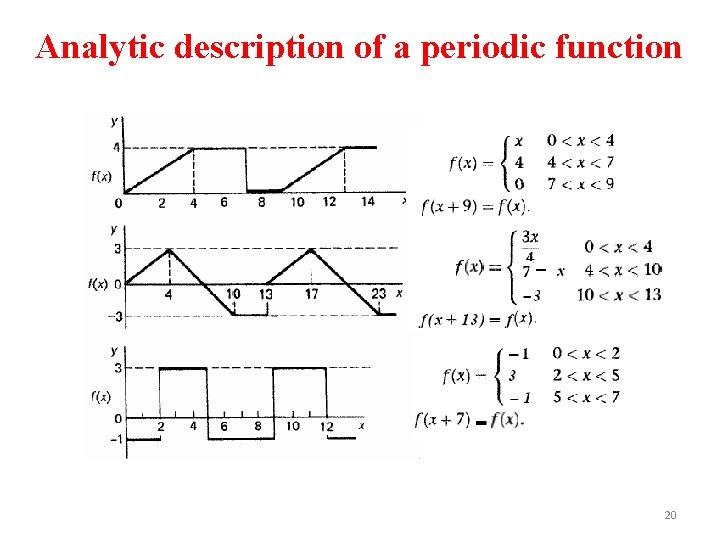
Analytic description of a periodic function 17

Analytic description of a periodic function 18

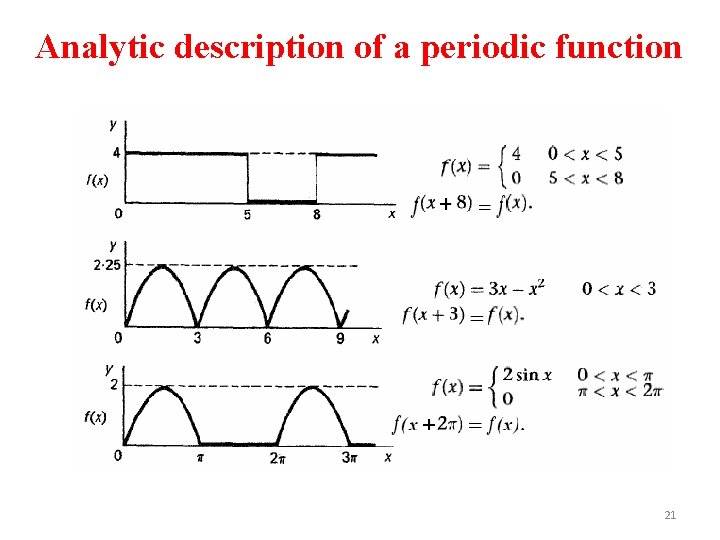
Analytic description of a periodic function 19

Analytic description of a periodic function 20

Analytic description of a periodic function 21

Orthogonal functions If two different functions f(x) and g(x) are defined on the interval a ≤x≤ b and Then we say that the two functions are orthogonal to each other on the interval a ≤x≤ b. The trigonometric functions sin(nx) and cos(nx) where n=0, 1, 2, …. Form an infinite collection of periodic functions that are mutually orthogonal on the interval , indeed on any interval of width That is 22

Fourier series We turn now to our main objective: the study of properties of linear combinations of the functions These functions are periodic with common period . Therefore, any linear combination is also periodic with period T. The most general function that can be so formed is an infinite sum: This is the Fourier series expansion of f(x) where the an and bn are constants called the Fourier coefficients. But how do we find the values of these constants? 23

Fourier coefficients 24

Fourier coefficients 25

Summary Fourier series 26

Dirichlet Conditions If a function f(t) is such that: (a) f(t) is defined, single-valued and periodic (b) f(t) and f ’(t) have at most a finite number of finite discontinuities over a single period – that is they are piecewise continuous. Then the series Where Converges to f(t) 27

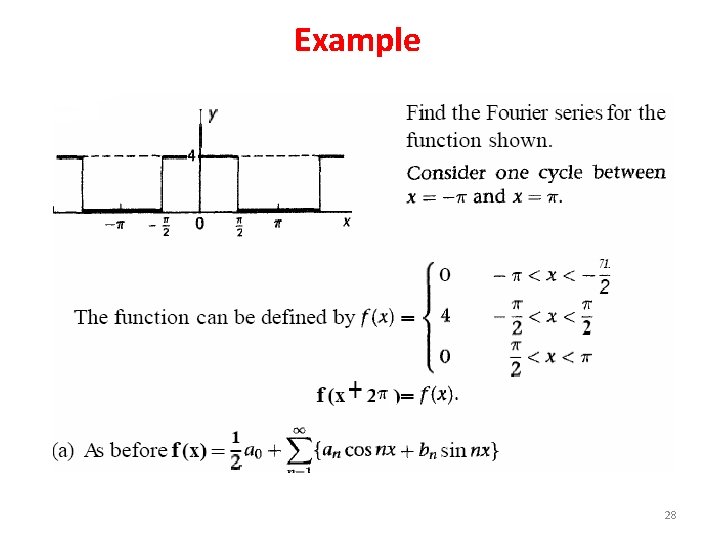
Example 28

29

30

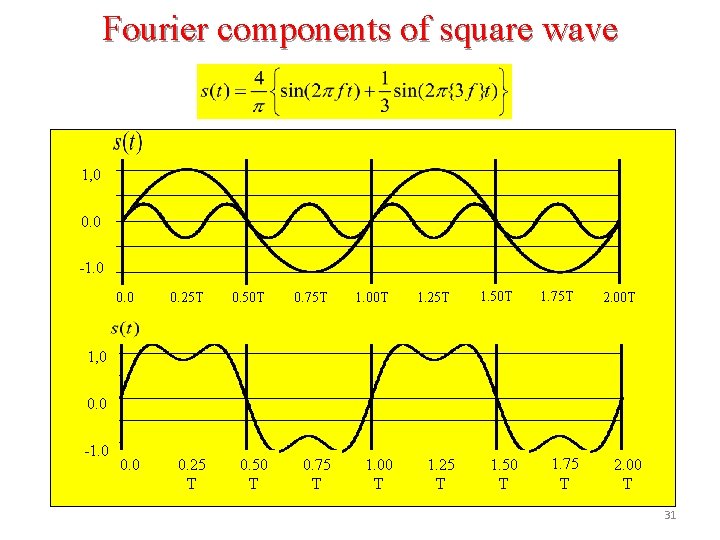
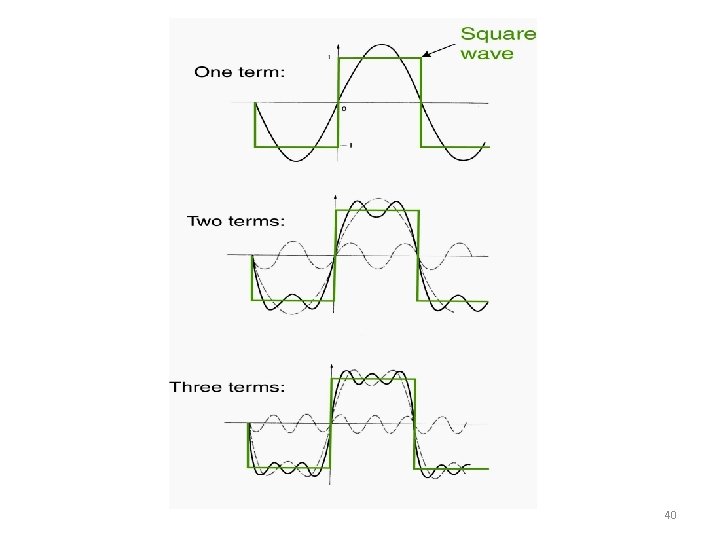
Fourier components of square wave 1, 0 0. 0 -1. 0 0. 25 T 0. 50 T 0. 75 T 0. 25 T 0. 50 T 0. 75 T 1. 00 T 1. 25 T 1. 50 T 1. 75 T 2. 00 T 1, 0 0. 0 -1. 0 0. 0 1. 00 T 1. 25 T 1. 50 T 1. 75 T 2. 00 T 31

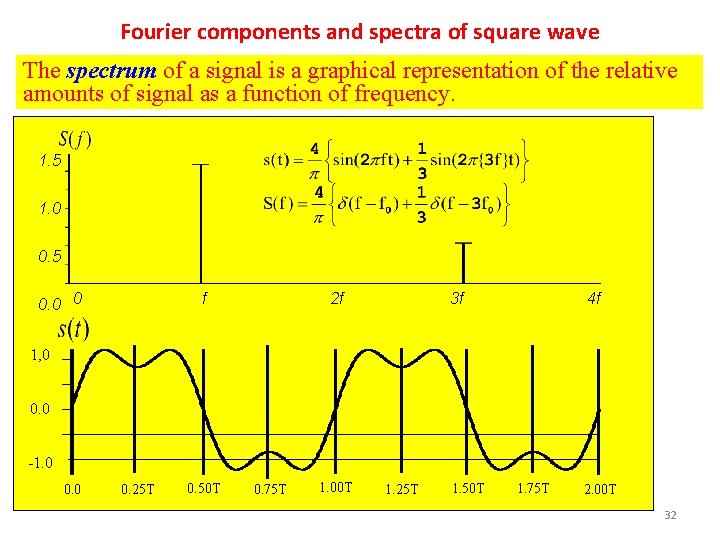
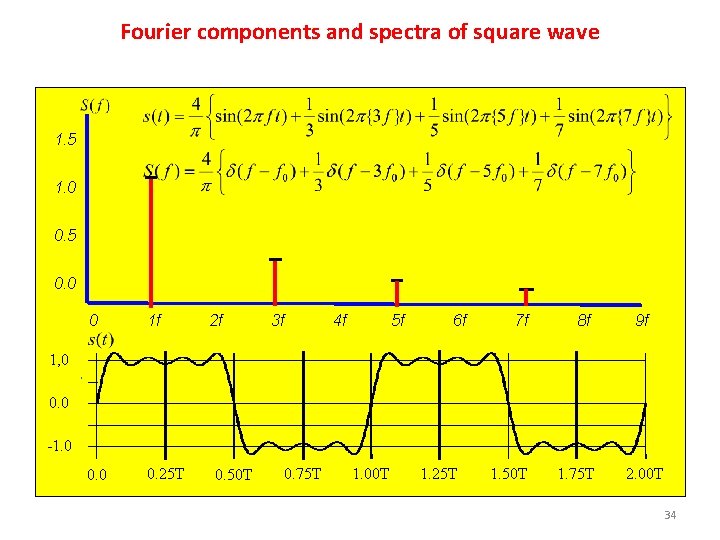
Fourier components and spectra of square wave The spectrum of a signal is a graphical representation of the relative amounts of signal as a function of frequency. 1. 5 1. 0 0. 5 0. 0 0 f 2 f 3 f 4 f 1, 0 . 0. 0 -1. 0 0. 25 T 0. 50 T 0. 75 T 1. 00 T 1. 25 T 1. 50 T 1. 75 T 2. 00 T 32

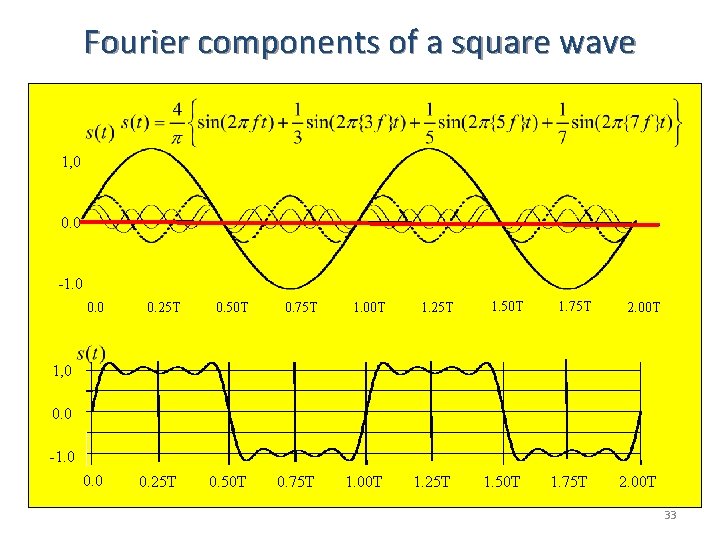
Fourier components of a square wave 1, 0 0. 0 -1. 0 0. 25 T 0. 50 T 0. 75 T 1. 00 T 1. 25 T 1. 50 T 1. 75 T 2. 00 T 0. 0 0. 25 T 0. 50 T 0. 75 T 1. 00 T 1. 25 T 1. 50 T 1. 75 T 2. 00 T 1, 0 0. 0 -1. 0 33

Fourier components and spectra of square wave 1. 5 1. 0 0. 5 0. 0 0 1 f 0. 0 0. 25 T 2 f 3 f 4 f 5 f 6 f 7 f 8 f 1. 50 T 1. 75 T 9 f 1, 0 0. 0 -1. 0 0. 50 T 0. 75 T 1. 00 T 1. 25 T 2. 00 T 34

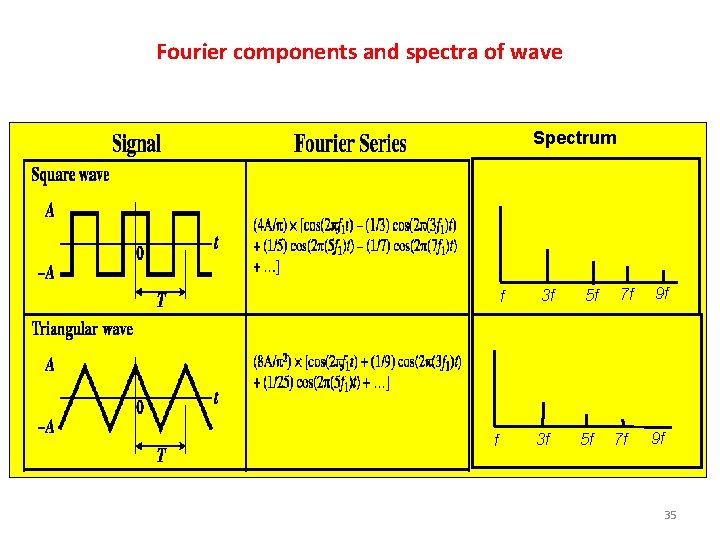
Fourier components and spectra of wave Spectrum f f 3 f 3 f 5 f 5 f 7 f 7 f 9 f 9 f 35

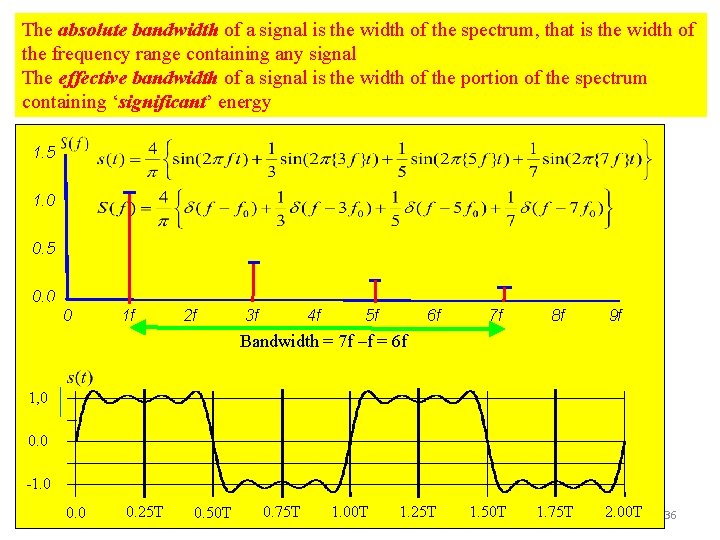
The absolute bandwidth of a signal is the width of the spectrum, that is the width of the frequency range containing any signal The effective bandwidth of a signal is the width of the portion of the spectrum containing ‘significant’ energy 1. 5 1. 0 0. 5 0. 0 0 1 f 2 f 3 f 4 f 5 f 6 f 7 f 1. 25 T 1. 50 T 8 f 9 f Bandwidth = 7 f –f = 6 f 1, 0 0. 0 -1. 0 0. 25 T 0. 50 T 0. 75 T 1. 00 T 1. 75 T 2. 00 T 36

37

38

39

40

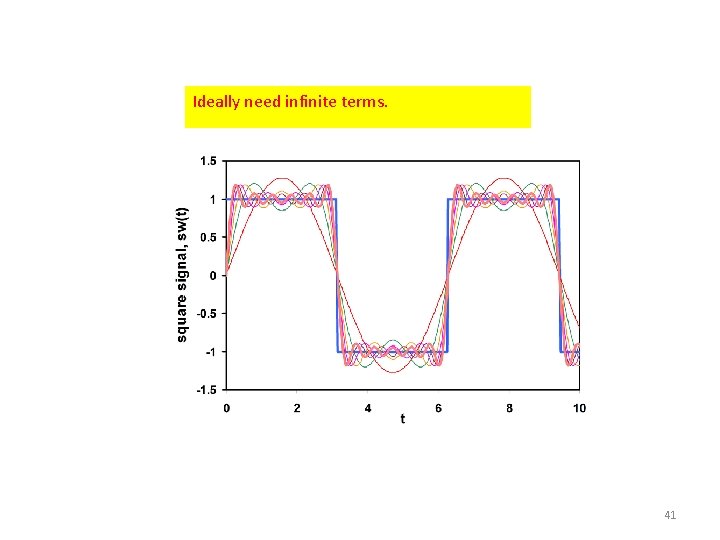
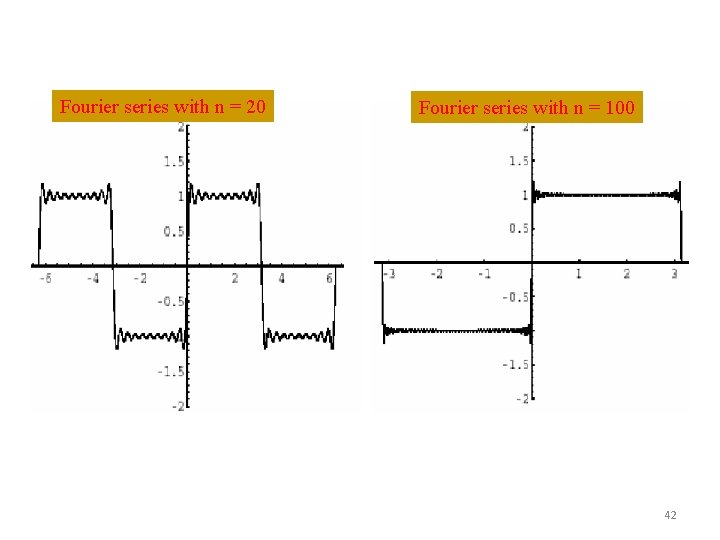
Ideally need infinite terms. 41

Fourier series with n = 20 Fourier series with n = 100 42

43

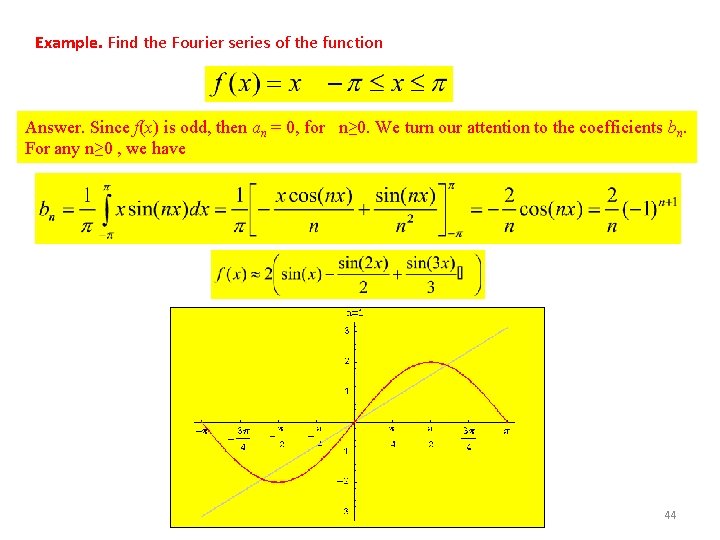
Example. Find the Fourier series of the function Answer. Since f(x) is odd, then an = 0, for n≥ 0. We turn our attention to the coefficients bn. For any n≥ 0 , we have 44

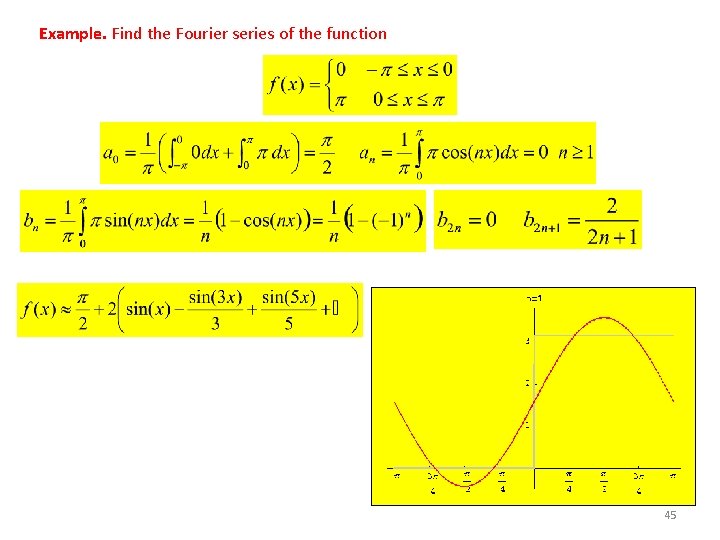
Example. Find the Fourier series of the function 45

Example. Find the Fourier series of the function Since this function is the function of the example above minus the constant So Therefore, the Fourier series of f(x) is . 46

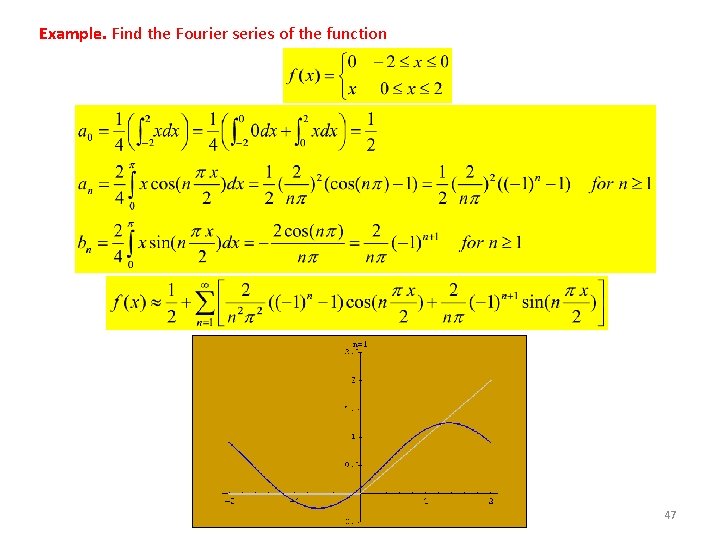
Example. Find the Fourier series of the function 47

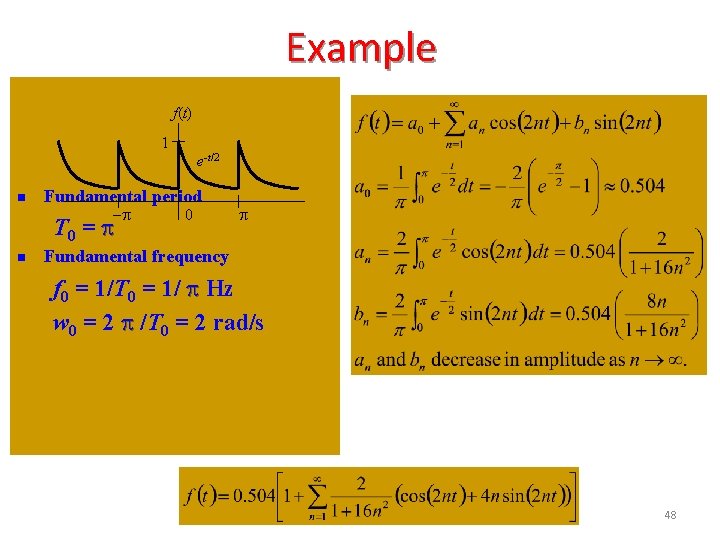
Example f(t) 1 e-t/2 n Fundamental period -p T 0 = p n 0 p Fundamental frequency f 0 = 1/T 0 = 1/ p Hz w 0 = 2 p /T 0 = 2 rad/s 48

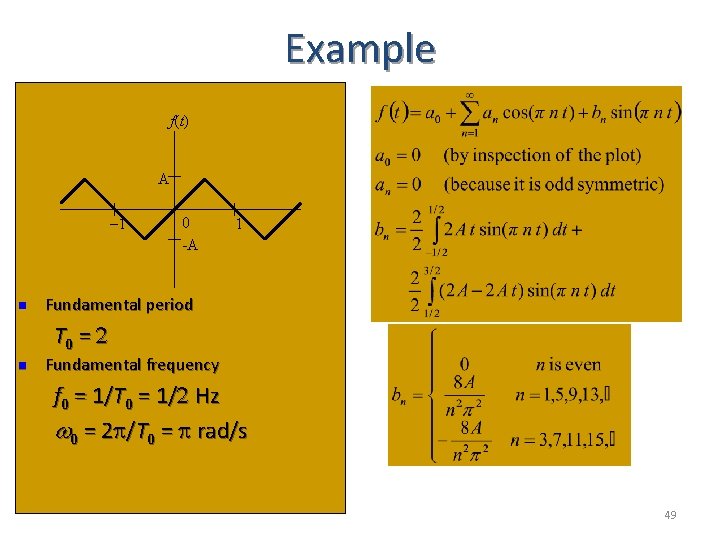
Example f(t) A -1 n 0 -A 1 Fundamental period T 0 = 2 n Fundamental frequency f 0 = 1/T 0 = 1/2 Hz w 0 = 2 p/T 0 = p rad/s 49

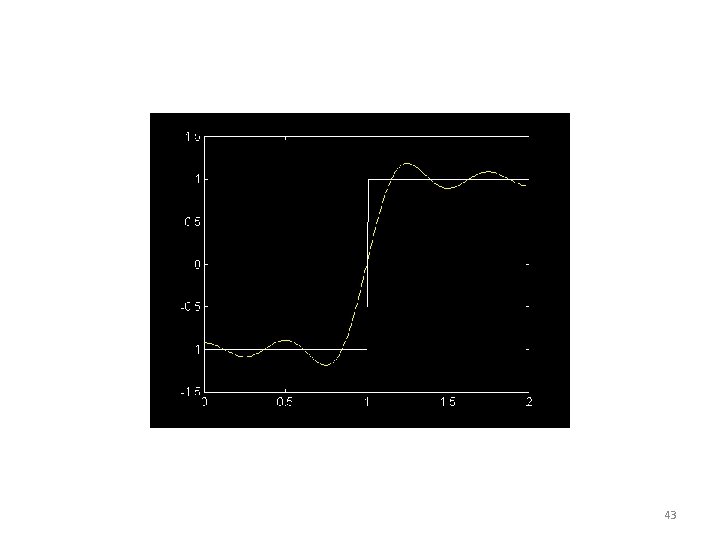
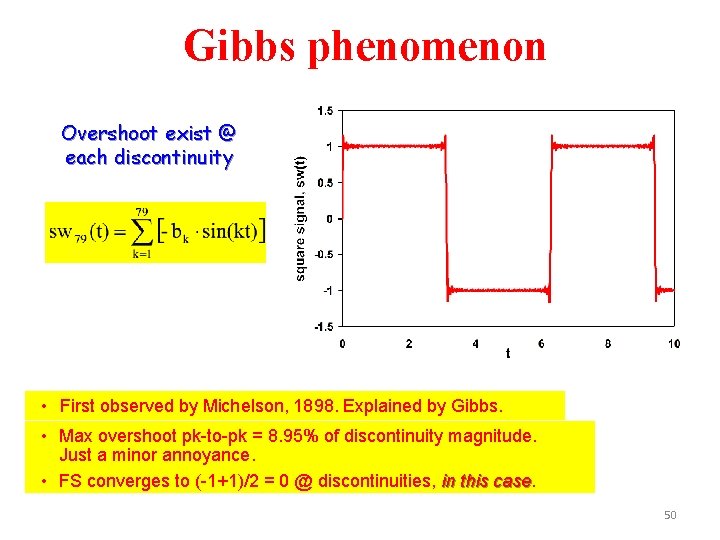
Gibbs phenomenon Overshoot exist @ each discontinuity • First observed by Michelson, 1898. Explained by Gibbs. • Max overshoot pk-to-pk = 8. 95% of discontinuity magnitude. Just a minor annoyance. • FS converges to (-1+1)/2 = 0 @ discontinuities, in this case 50

Questions? Discussion? Suggestions ?

52