Drawings as Models of Syntactic Structure Theory and

Drawings as Models of Syntactic Structure: Theory and Algorithms by Mathias Möhl supervised by Marco Kuhlmann final talk of diploma thesis at Programming Systems Lab. Saarland University, Prof. Smolka

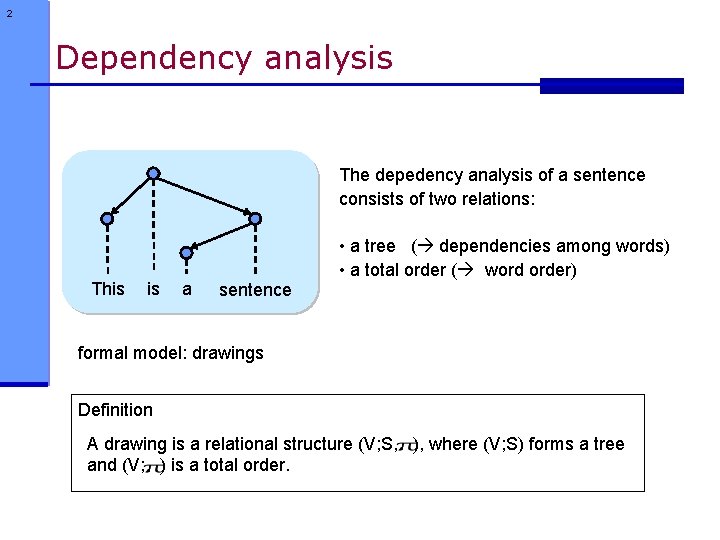
2 Dependency analysis The depedency analysis of a sentence consists of two relations: This is a sentence • a tree ( dependencies among words) • a total order ( word order) formal model: drawings Definition A drawing is a relational structure (V; S, ), where (V; S) forms a tree and (V; ) is a total order.

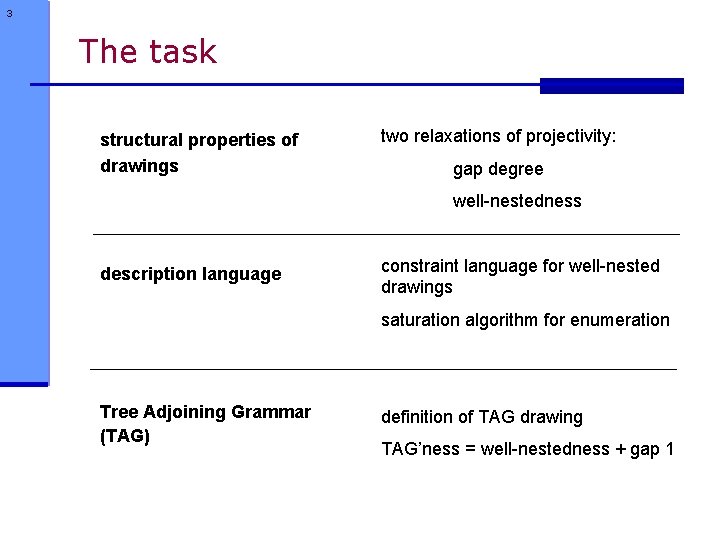
3 The task structural properties of drawings two relaxations of projectivity: gap degree well-nestedness description language constraint language for well-nested drawings saturation algorithm for enumeration Tree Adjoining Grammar (TAG) definition of TAG drawing TAG’ness = well-nestedness + gap 1

4 Part I Structural properties of drawings

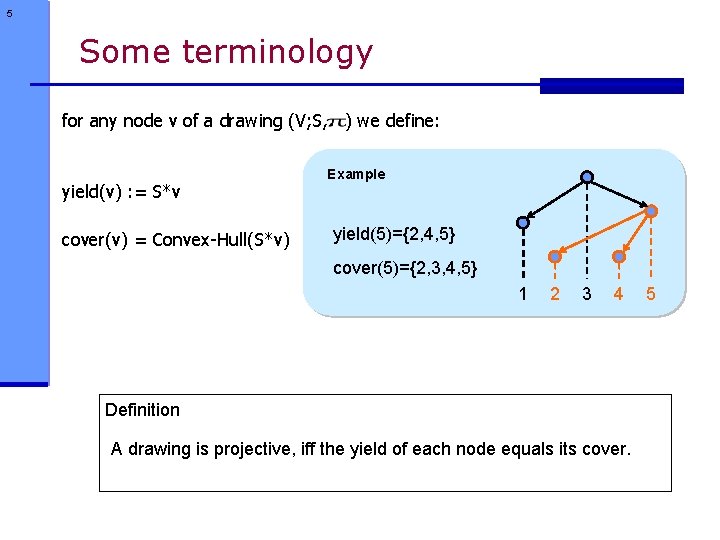
5 Some terminology for any node v of a drawing (V; S, ) we define: yield(v) : = S*v cover(v) = Convex-Hull(S*v) Example yield(5)={2, 4, 5} cover(5)={2, 3, 4, 5} 1 2 3 4 Definition A drawing is projective, iff the yield of each node equals its cover. 5

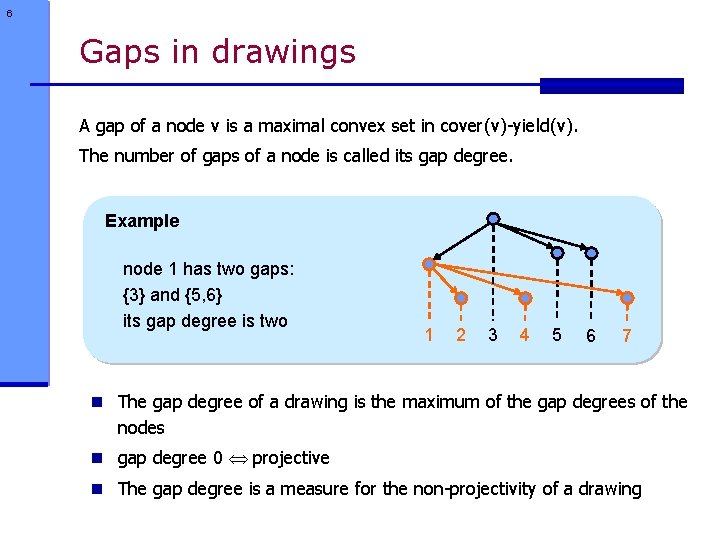
6 Gaps in drawings A gap of a node v is a maximal convex set in cover(v)-yield(v). The number of gaps of a node is called its gap degree. Example node 1 has two gaps: {3} and {5, 6} its gap degree is two 1 2 3 4 5 6 7 n The gap degree of a drawing is the maximum of the gap degrees of the nodes n gap degree 0 projective n The gap degree is a measure for the non-projectivity of a drawing

7 Contributions related to gaps n Algorithm to compute the gap degree O(n*g) (n= number of nodes; g=gap degree ; g<n) n A drawing has at most O(n²) gaps and at most O(n*log(n)) different gaps worst case examples O(n²) 1 2 3 4 5 6 7 O(n*log(n)) 1 2 3 4 5 6 7

8 Well- nestedness n Well-nestedness is a second kind of relaxation of projectivity n Orthogonal to the gap degree Definition A drawing is well-nested if is satisfies the constraint: All disjoint subtrees are non-interleaving. Two subtrees T 1, T 2 interleave, if there are nodes l 1, r 1 T 1 and l 2, r 2 T 2 such that l 1 l 2 r 1 r 2. non-interleaving subtrees l 1 r 1 l 2 r 2 l 1 projective well-nested l 2 r 1 interleaving subtrees r 2 l 1 l 2 r 1 r 2

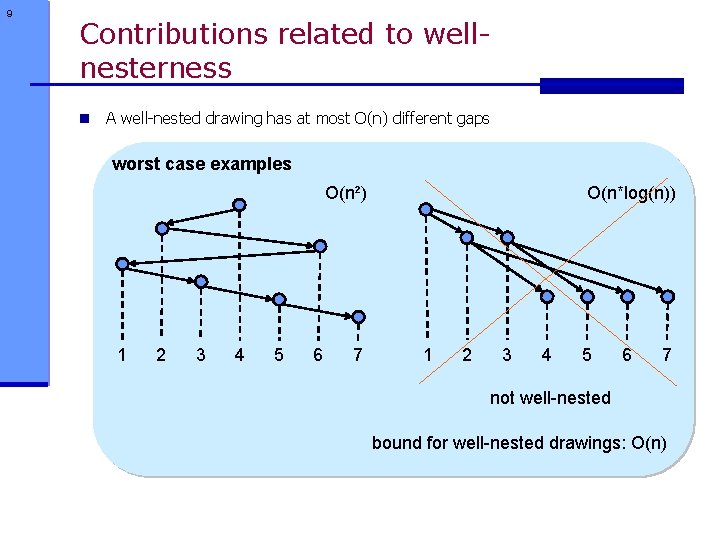
9 Contributions related to wellnesterness n A well-nested drawing has at most O(n) different gaps worst case examples O(n²) 1 2 3 4 5 6 7 O(n*log(n)) 1 2 3 4 5 6 7 not well-nested bound for well-nested drawings: O(n)

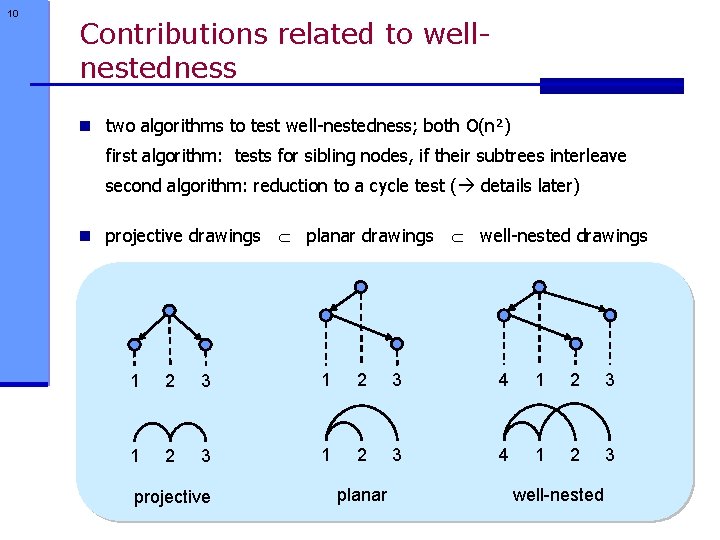
10 Contributions related to wellnestedness n two algorithms to test well-nestedness; both O(n²) first algorithm: tests for sibling nodes, if their subtrees interleave second algorithm: reduction to a cycle test ( details later) n projective drawings planar drawings well-nested drawings 1 2 3 4 1 2 3 projective planar well-nested

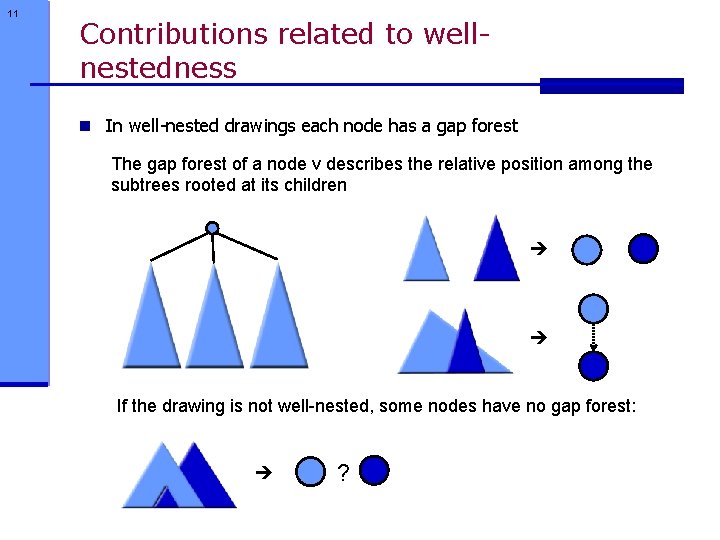
11 Contributions related to wellnestedness n In well-nested drawings each node has a gap forest The gap forest of a node v describes the relative position among the subtrees rooted at its children If the drawing is not well-nested, some nodes have no gap forest: ?

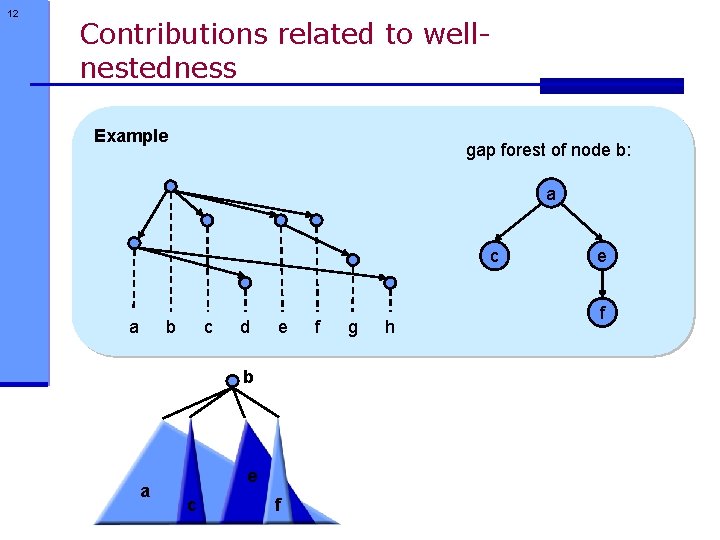
12 Contributions related to wellnestedness Example gap forest of node b: a c a b c d e b a e c f f g h e f

13 Part II A description language for drawings

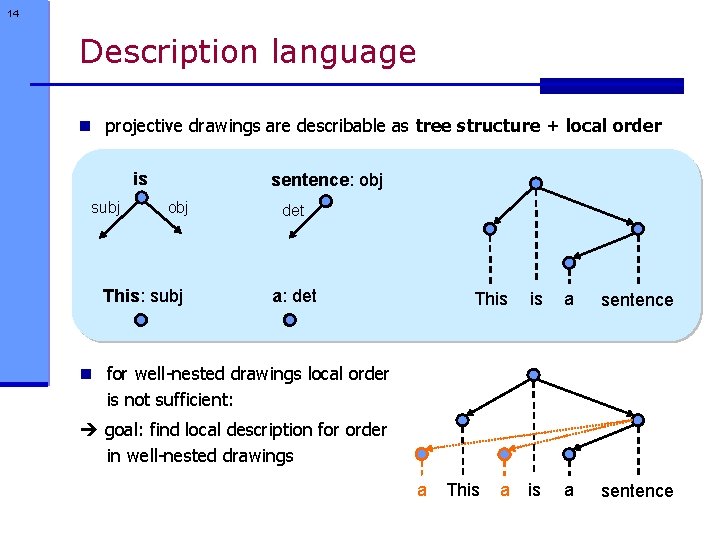
14 Description language n projective drawings are describable as tree structure + local order is subj sentence: obj This: subj det a: det This is a sentence n for well-nested drawings local order is not sufficient: goal: find local description for order in well-nested drawings a This a

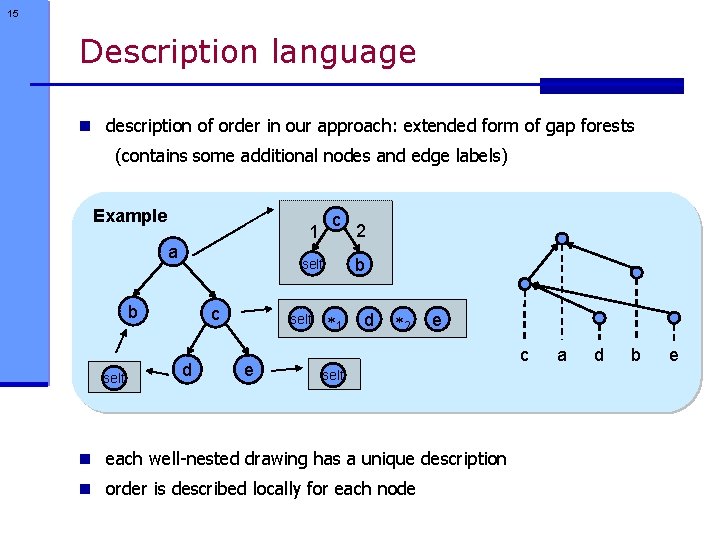
15 Description language n description of order in our approach: extended form of gap forests (contains some additional nodes and edge labels) Example a c d self e 2 b self c 1 1 d 2 e c self n each well-nested drawing has a unique description n order is described locally for each node a d b e

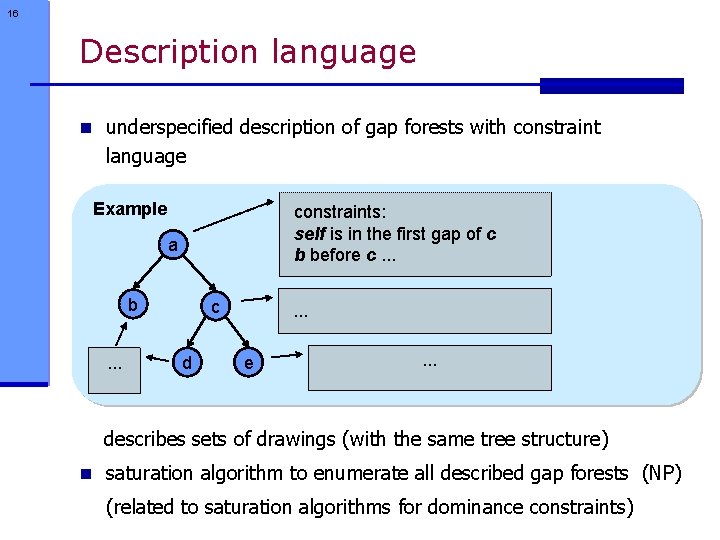
16 Description language n underspecified description of gap forests with constraint language Example constraints: self is in the first gap of c b before c. . . a b. . . c d . . . e . . . describes sets of drawings (with the same tree structure) n saturation algorithm to enumerate all described gap forests (NP) (related to saturation algorithms for dominance constraints)

17 Part III Tree Adjoining Grammar

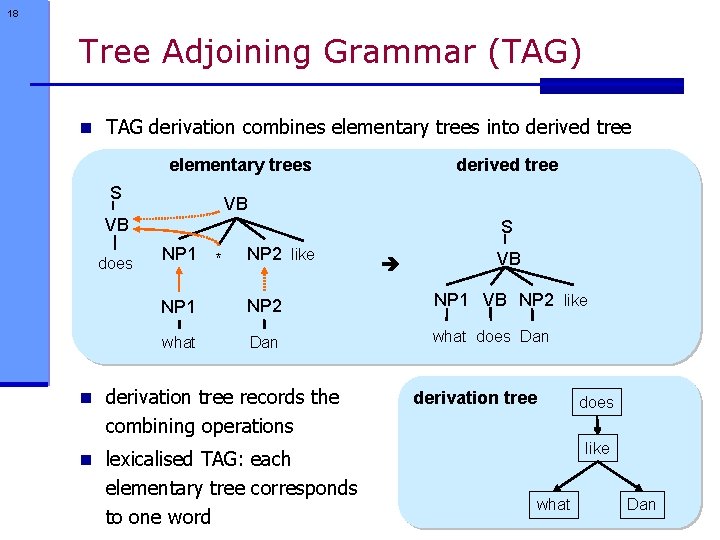
18 Tree Adjoining Grammar (TAG) n TAG derivation combines elementary trees into derived tree elementary trees S derived tree VB VB does S NP 1 * NP 2 like VB NP 1 NP 2 NP 1 VB NP 2 like what Dan what does Dan n derivation tree records the derivation tree does combining operations like n lexicalised TAG: each elementary tree corresponds to one word what Dan

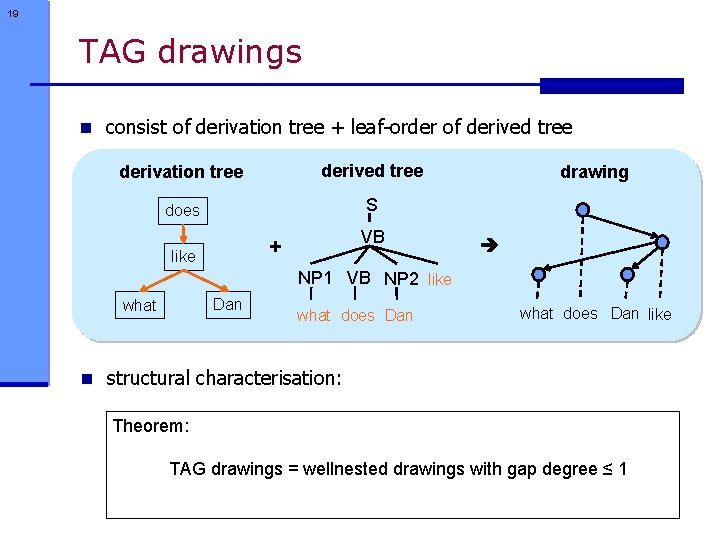
19 TAG drawings n consist of derivation tree + leaf-order of derived tree derivation tree derived tree does S VB + like drawing NP 1 VB NP 2 like Dan what does Dan like n structural characterisation: Theorem: TAG drawings = wellnested drawings with gap degree ≤ 1

20 finally a technical detail: Reducing wellnestednessto a cycle-test

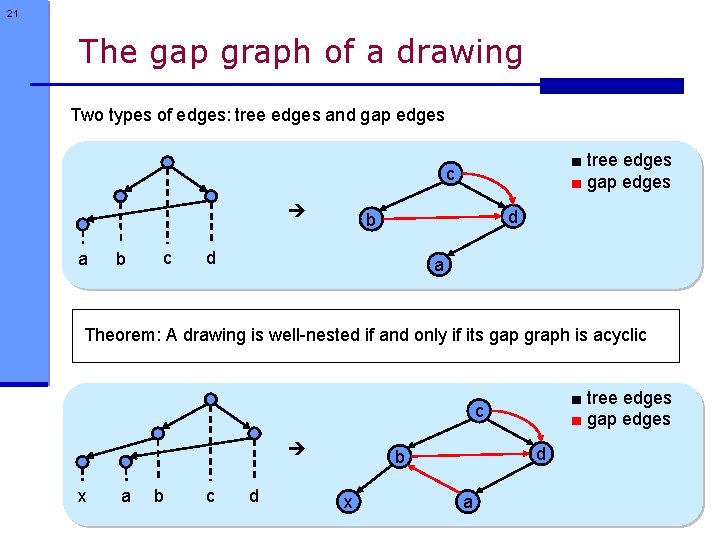
21 The gap graph of a drawing Two types of edges: tree edges and gap edges ■ tree edges ■ gap edges c a b c d b d a Theorem: A drawing is well-nested if and only if its gap graph is acyclic ■ tree edges ■ gap edges c x a b c d d b x a

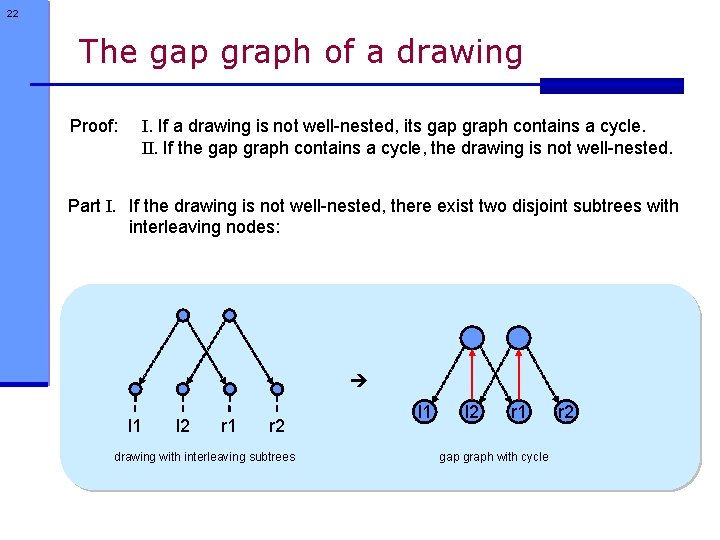
22 The gap graph of a drawing Proof: I. If a drawing is not well-nested, its gap graph contains a cycle. II. If the gap graph contains a cycle, the drawing is not well-nested. Part I. If the drawing is not well-nested, there exist two disjoint subtrees with interleaving nodes: l 1 l 2 r 1 r 2 drawing with interleaving subtrees l 1 l 2 r 1 gap graph with cycle r 2

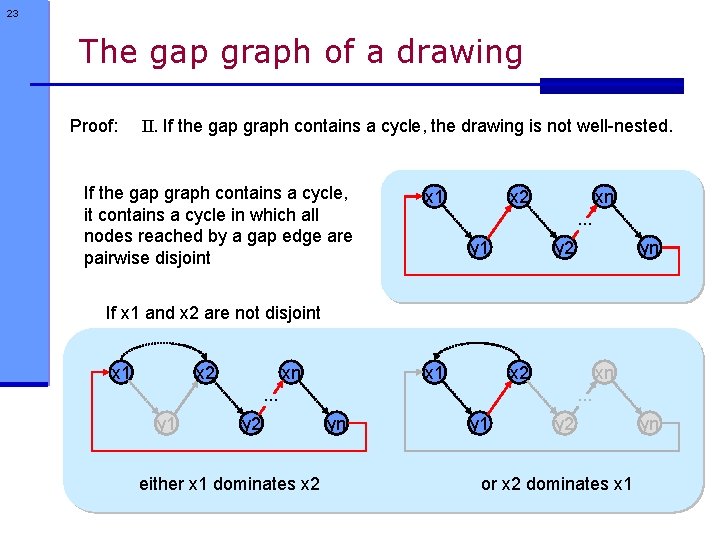
23 The gap graph of a drawing Proof: II. If the gap graph contains a cycle, the drawing is not well-nested. If the gap graph contains a cycle, it contains a cycle in which all nodes reached by a gap edge are pairwise disjoint x 1 x 2 xn. . . y 1 y 2 yn If x 1 and x 2 are not disjoint x 1 x 2 xn . . . y 1 y 2 either x 1 dominates x 2 . . . yn y 1 y 2 or x 2 dominates x 1 yn

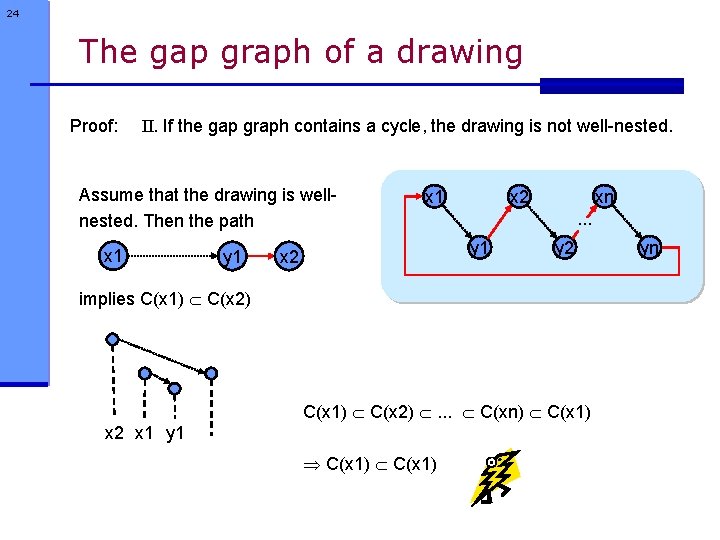
24 The gap graph of a drawing Proof: II. If the gap graph contains a cycle, the drawing is not well-nested. Assume that the drawing is wellnested. Then the path x 1 y 1 x 2. . . y 1 x 2 xn y 2 implies C(x 1) C(x 2) . . . C(xn) C(x 1) x 2 x 1 y 1 C(x 1) yn

25 Main contributions n Formalisation of drawings n Measures for non-projectivity of drawings: n gap-degree n well-nestedness n Description language for well-nested drawings. n Characterisation of TAG drawings (well-nested + gap 1) Future work: n tree bank evaluations n grammar formalism based on drawings n structural properties of other formalisms

26 References Manuel Bodirsky, Marco Kuhlmann, and Mathias Möhl. Well-nested drawings as models of syntactic structure. In 10 th Conference on Formal Grammar and 9 th Meeting on Mathematics of Language, Edinburgh, Scotland, UK, 2005. Manuel Bodirsky and Martin Kutz. Pure dominance constraints. In Proceedings of the 19 th Annual Symposium on Theoretical Aspects of Computer Science (STACS 2002), 2002. Mike Daniels and W. Detmar Meurers. Improving the efficiency of parsing with discontinuous constituents. In Shuly Wintner, editor, Proceedings of NLULP’ 02: The 7 th International Workshop on Natural Language Understanding and Logic Programming, number 92 in Datalogiske Skrifter, pages 49– 68, Copenhagen, 2002. Roskilde Universitetscenter. Denys Duchier and Joachim Niehren. Dominance constraints with set operators. In Proceedings of the First International Conference on Computational Logic (CL 2000), volume 1861 of Lecture Notes in Computer Science, pages 326– 341. Springer, July 2000.

27 References Alexander Koller. Constraint-based and graph-based resolution of ambiguities in natural language. Ph. D thesis, Universität des Saarlandes, 2004. Martin Plátek, Tomáš Holan, and Vladislav Kuboˇn. On relax-ability of word-order by d-grammars. In Cristian Calude, Michael Dinneen, and Smaranda Sburlan, editors, Combinatorics, Computability and Logic, Discrete Mathematics and Theoretical Computer Science, pages 159– 174. Springer, Berlin, 2001. Anssi Yli-Jyrä. Multiplanarity – a model for dependency structures in treebanks. In Second Workshop on Treebanks and Linguistic Theories, Mathematical Modelling in Physics, Engineering and Cognitive Sciences, pages 189– 200, Växjö, Sweden, 2003.