DRAWING GRAPHS FROM EQUATIONS Objectives Learn how to

DRAWING GRAPHS FROM EQUATIONS

Objectives Learn how to calculate coordinates specific to an equation Learn how to draw a graph of any equation

Key points • Make sure your pencil is sharp • Restrict use of eraser • Work out your coordinates • Work out your scale, be consistent! • Label axis • Join points with ruler • Label the line • Give your graph a title

Drawing Graphs from Equations A graph can be drawn from any equation. For example, draw the graph of: y = 2 x This means double x

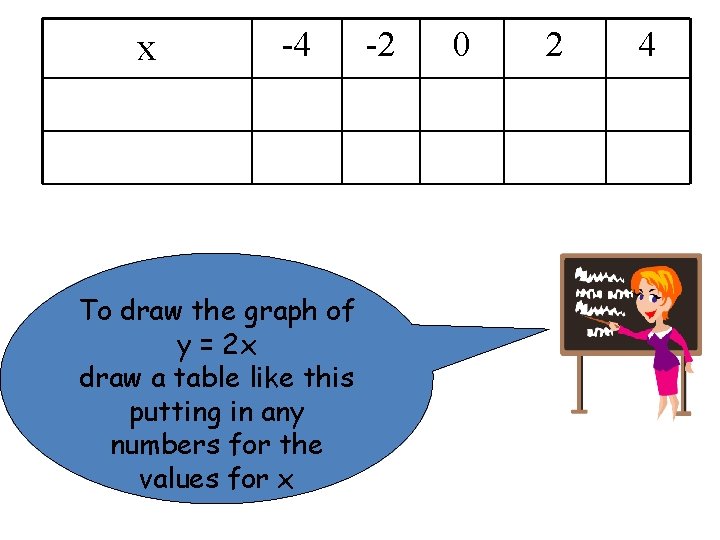
x -4 To draw the graph of y = 2 x draw a table like this putting in any numbers for the values for x -2 0 2 4

x -4 -2 0 2 4 2 x -8 -4 0 4 8 I want to find y = 2 x , so for every value of x we multiply by 2 for 2 x.

x -4 -2 0 2 4 2 x -8 -8 -4 -4 0 0 4 4 8 8 y You have multiplied all the x numbers so now you have found the corresponding y numbers for y = 2 x

x -4 -2 0 2 4 y -8 -4 0 4 8 (-4, -8) (-2, -4) (0, 0) (2, 4) (4, 8) Now you have your set of coordinates you are ready to plot the graph

Graph of equation y = 2 x y 10 y = 2 x 9 8 x y -4 -8 -2 -4 7 y = 2 x 6 5 4 3 0 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 1 2 3 4 5 6 7 8 9 10 x 0 2 4 4 8

Drawing Graphs from Equations Now lets draw the graph of: y = 2 x + 1 This means double x and then add 1

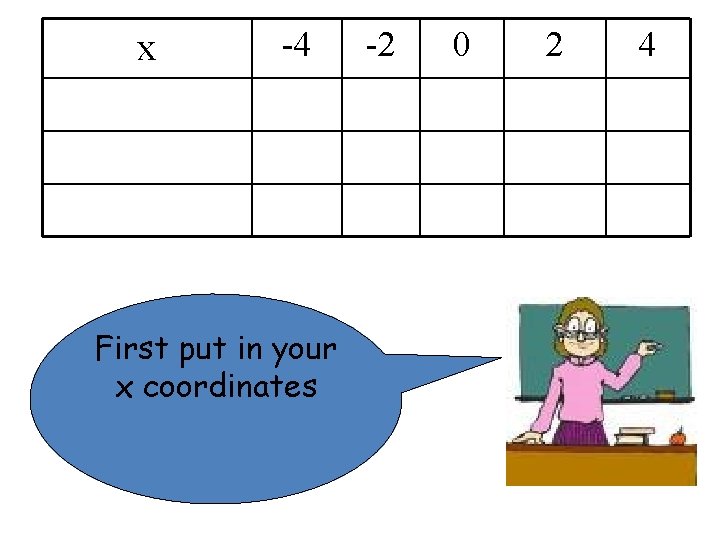
x -4 First put in your x coordinates -2 0 2 4

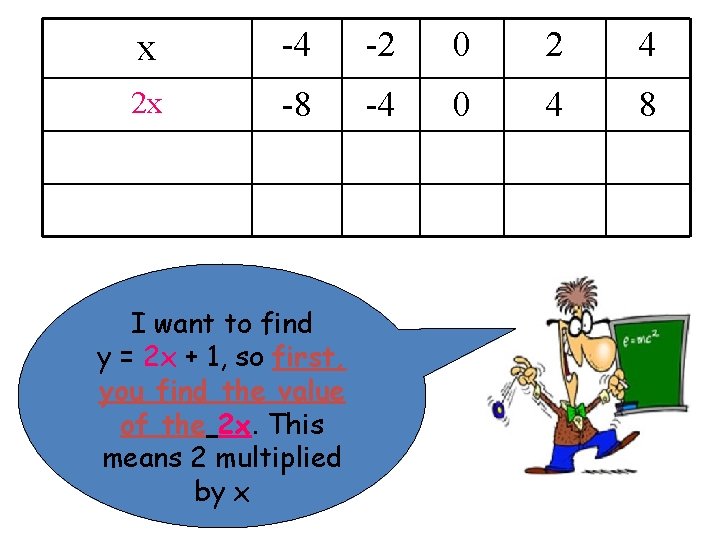
x -4 -2 0 2 4 2 x -8 -4 0 4 8 I want to find y = 2 x + 1, so first, you find the value of the 2 x. This means 2 multiplied by x

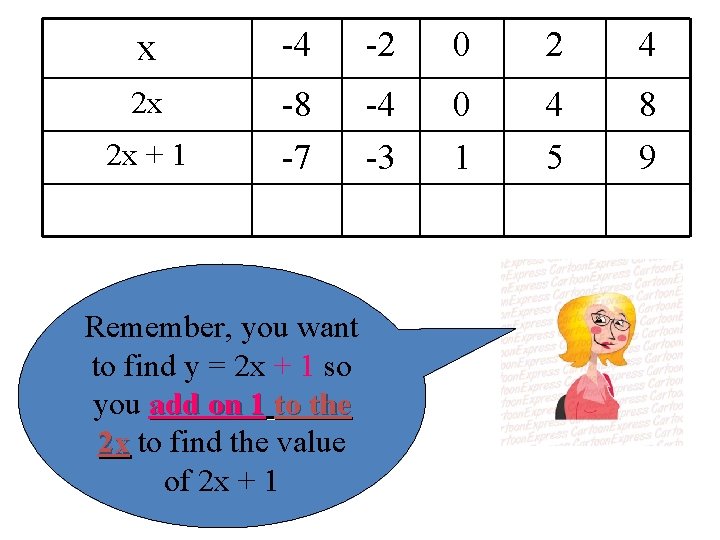
x -4 -2 0 2 4 2 x -8 -7 -4 -3 0 1 4 5 8 9 2 x + 1 Remember, you want to find y = 2 x + 1 so you add on 1 to the 2 x to find the value of 2 x + 1

x -4 -2 0 2 4 2 x -8 -7 -7 -4 -3 -3 0 1 1 4 5 5 8 9 9 2 x + 1 y Now you have the coordinates for y = 2 x + 1

x -4 -2 0 2 4 y -7 -3 1 5 9 Now, plot the value of x against the value of y on the graph’s axes.

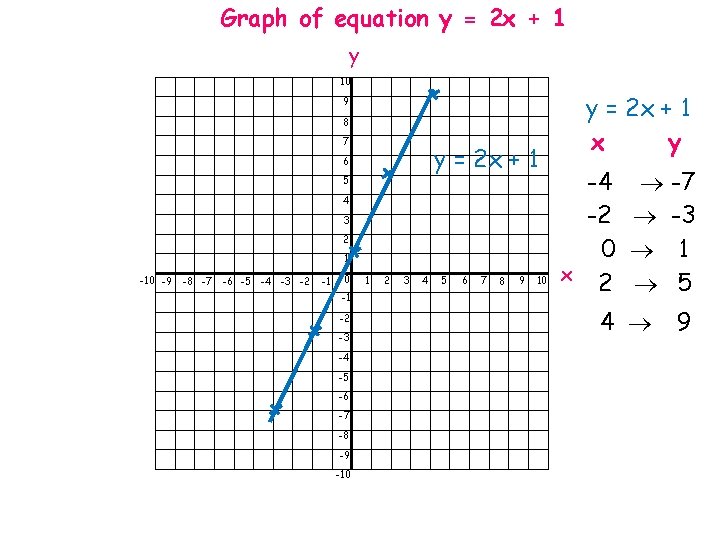
Graph of equation y = 2 x + 1 y 10 9 8 7 y = 2 x + 1 6 5 4 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 1 2 3 4 5 6 7 8 9 10 y = 2 x + 1 x y -4 -7 -2 -3 0 1 x 2 5 4 9

Draw the graph of: y = -½x - 3 x -4 -2 0 2 4

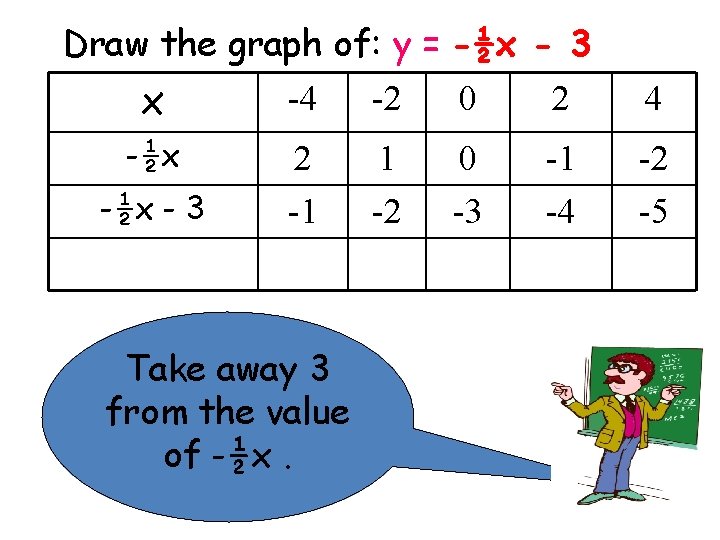
Draw the graph of: y = -½x - 3 x -4 -2 0 2 4 -½x 2 1 0 -1 -2 Find the value of -½x. You times all the x numbers by -½

Draw the graph of: y = -½x - 3 x -4 -2 0 2 4 -½x 2 -1 1 -2 0 -3 -1 -4 -2 -5 -½x - 3 Take away 3 from the value of -½x.

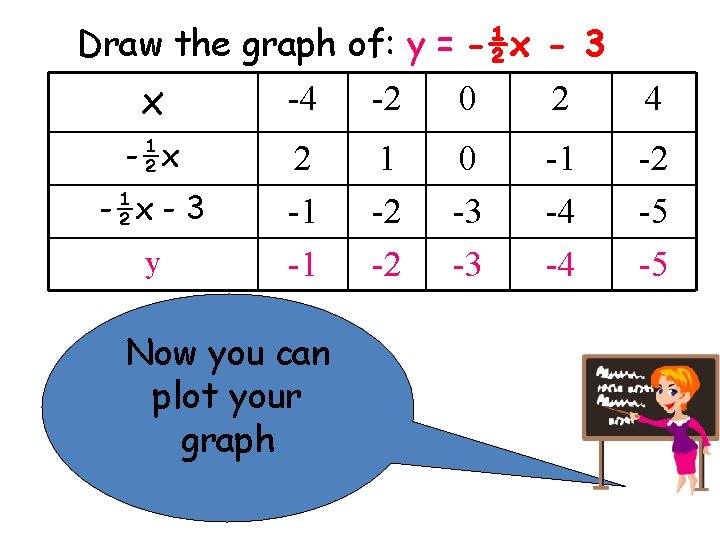
Draw the graph of: y = -½x - 3 x -4 -2 0 2 4 -½x 2 -1 -1 1 -2 -2 0 -3 -3 -1 -4 -4 -2 -5 -5 -½x - 3 y Now you can plot your graph

Draw the graph of: y = -½x - 3 x -4 -2 0 2 4 y -1 -2 -3 -4 -5 Now you can plot your graph

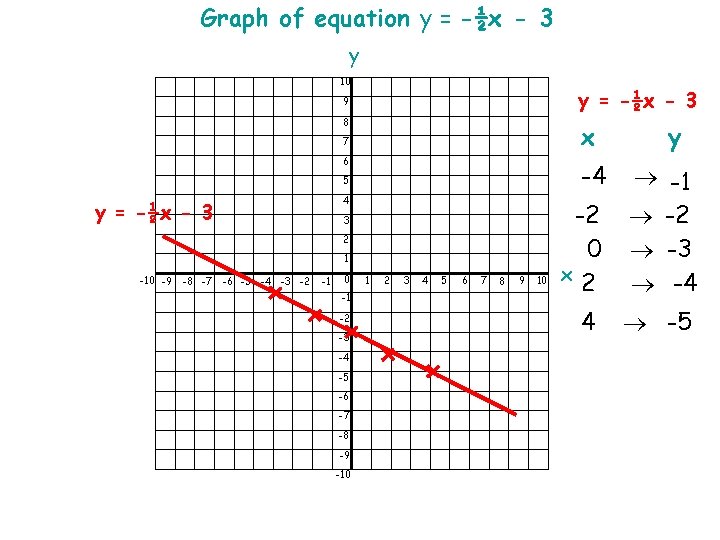
Graph of equation y = -½x - 3 y 10 y = -½x - 3 9 8 x 7 6 -4 5 4 y = -½x - 3 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 1 2 3 4 5 6 7 8 9 10 y -2 0 x 2 -1 -2 -3 -4 4 -5

Equations of lines with only one letter You have learnt how to draw any line of equations in the form of y = 2 x + 3 What about equations where there is only 1 letter? �y =1 �x = 5

Equations of lines with only one letter Consider the points shown on the graph What do they all have in common? An x value equal to 1 • (1, 5) They also all lie in line • (1, 3) If we labelled some more points on the line, what would they have in common with these? They would also have an x value equal to 1 We can therefore say the equation of the line is x = 1 • (1, 1) • (1, 0) • (1, – 1 ) • (1, – 3) • (1, – 4)

Consider the points shown on this graph (5, 3) • We can therefore say the equation of the line is y = 3 • 3) (3, ) • 3 (2, They would also have a y value equal to 3 • 3) They also all lie in line If we labelled some more points on the line, what would they have in common with these points? (0, ) • , 3 (-2 ) • , 3 (-4 ) • , 3 (-5 What do they all have in common? A y value equal to 3

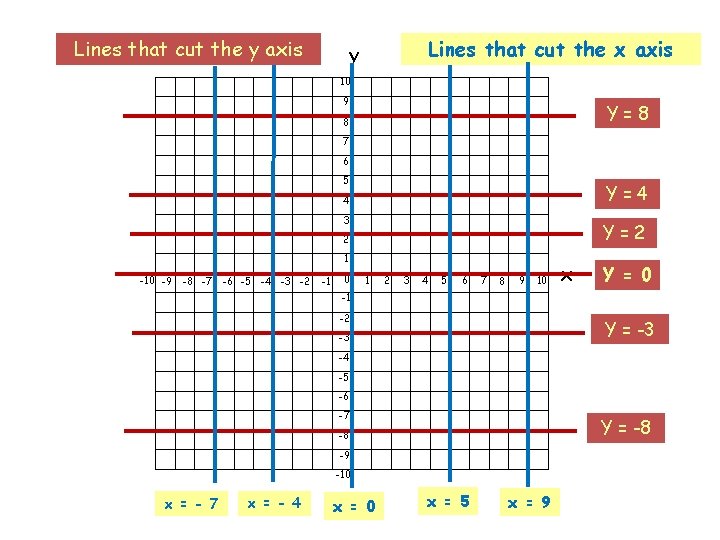
Lines that cut the y axis Lines that cut the x axis y 10 9 Y=8 8 7 6 5 Y=4 4 3 Y=2 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 x Y = 0 -1 -2 Y = -3 -3 -4 -5 -6 -7 Y = -8 -8 -9 -10 x = - 7 x = - 4 x = 0 x = 5 x = 9

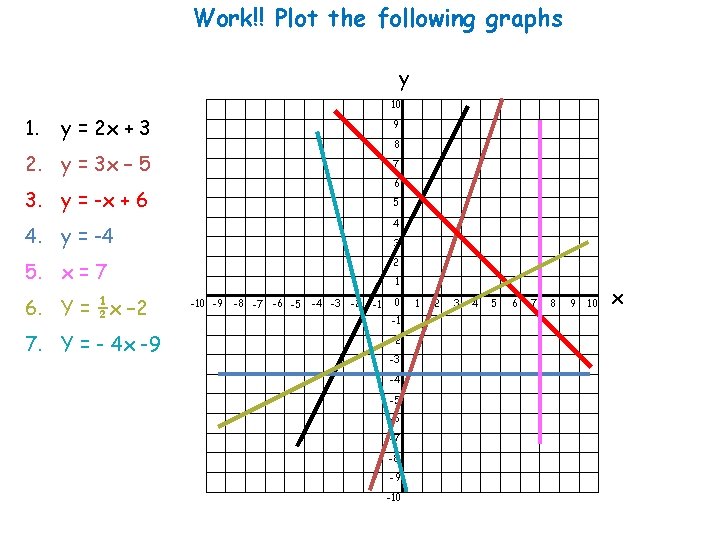
Work!! Plot the following graphs y 10 1. y = 2 x + 3 9 2. y = 3 x – 5 7 3. y = -x + 6 5 8 6 4. y = -4 4 5. x = 7 2 6. Y = ½x – 2 7. Y = - 4 x -9 3 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 1 2 3 4 5 6 7 8 9 10 x