Draw the next two terms in this sequence



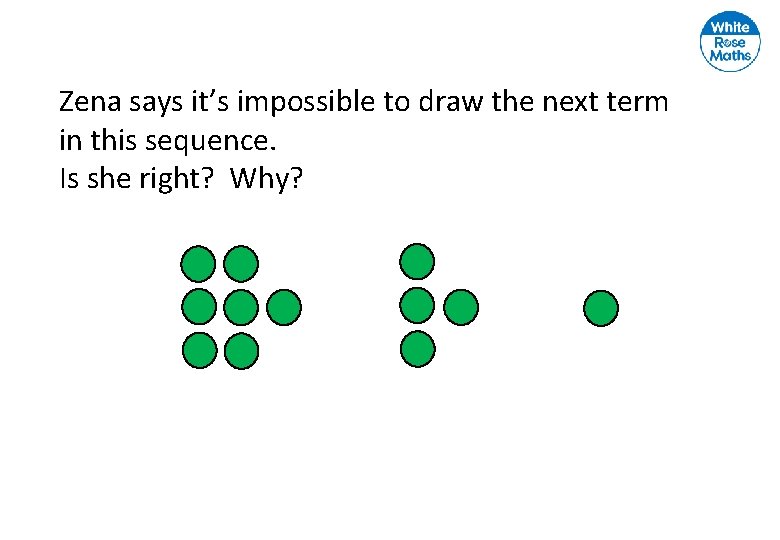

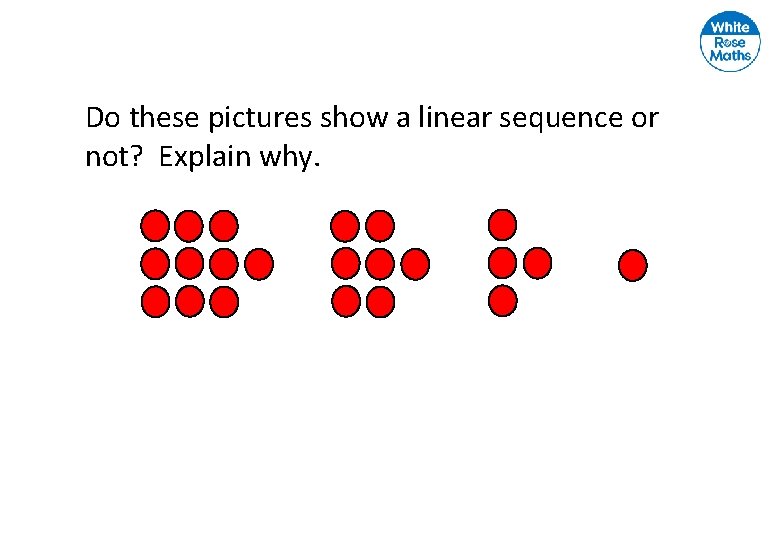


















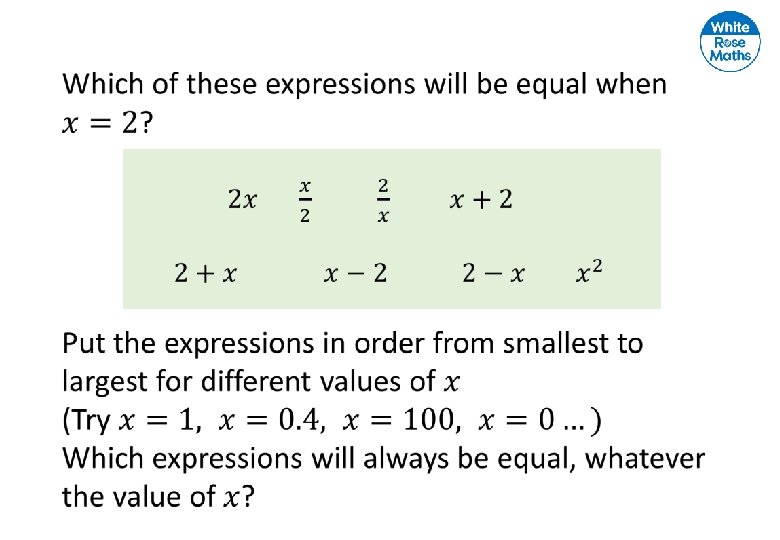
















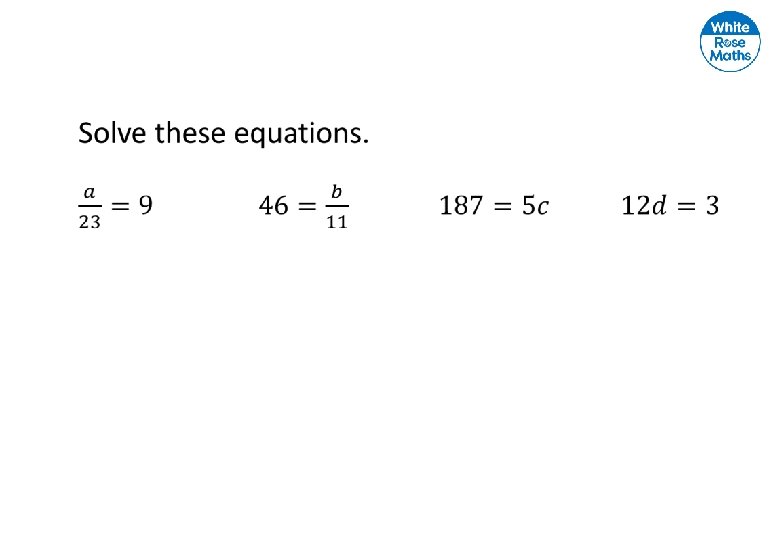





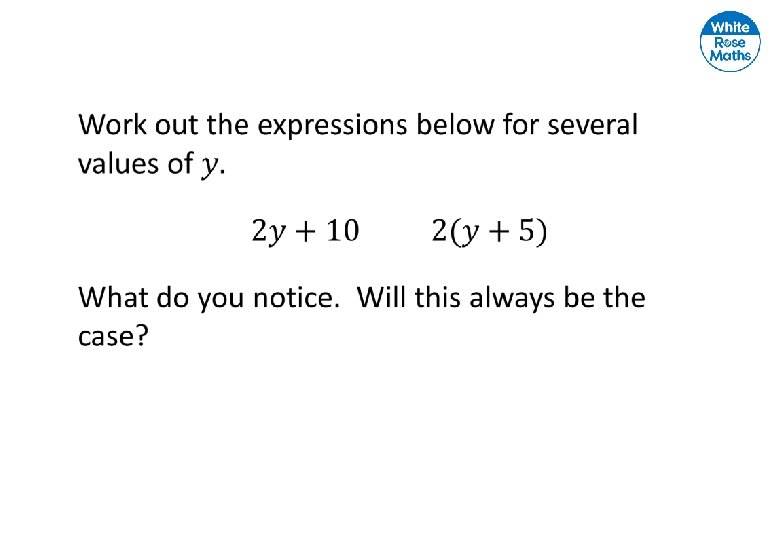




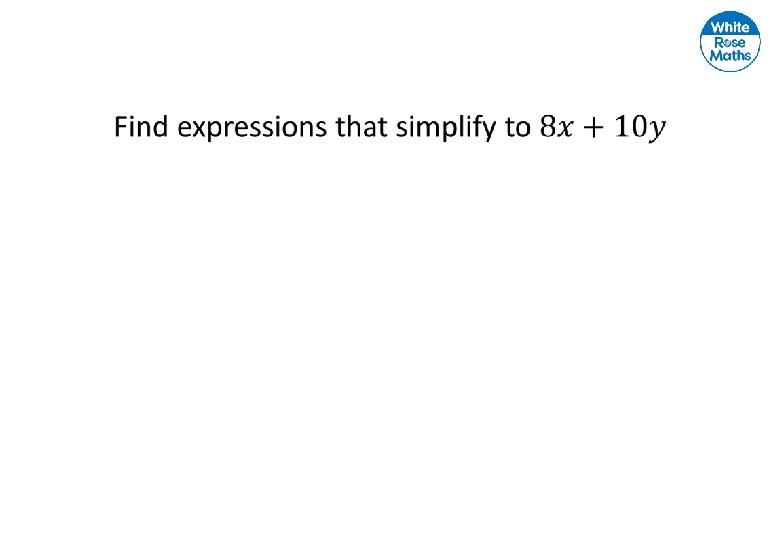
- Slides: 93




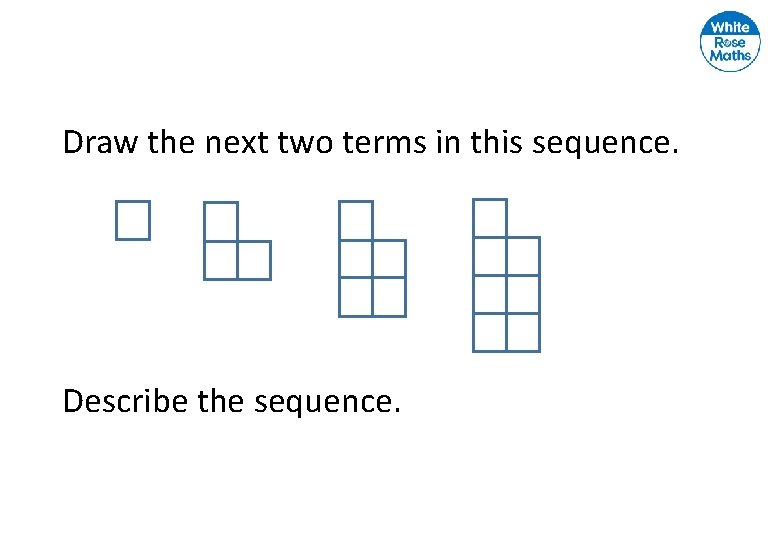
Draw the next two terms in this sequence. Describe the sequence.

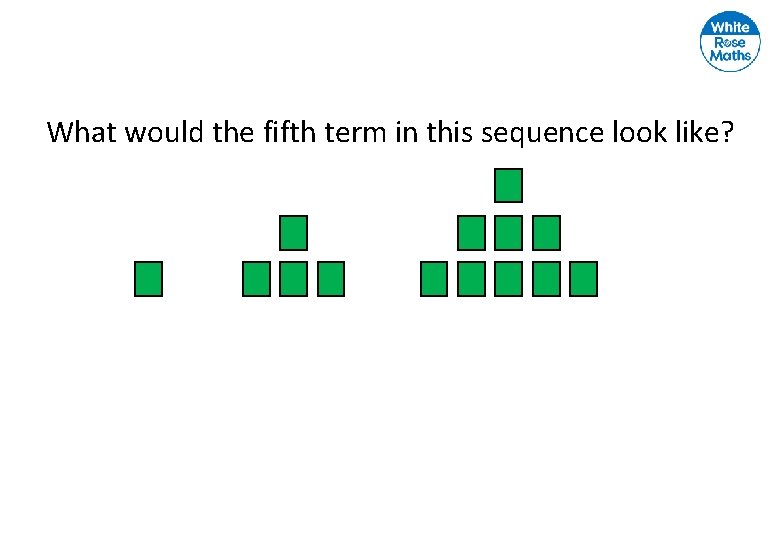
What would the fifth term in this sequence look like?

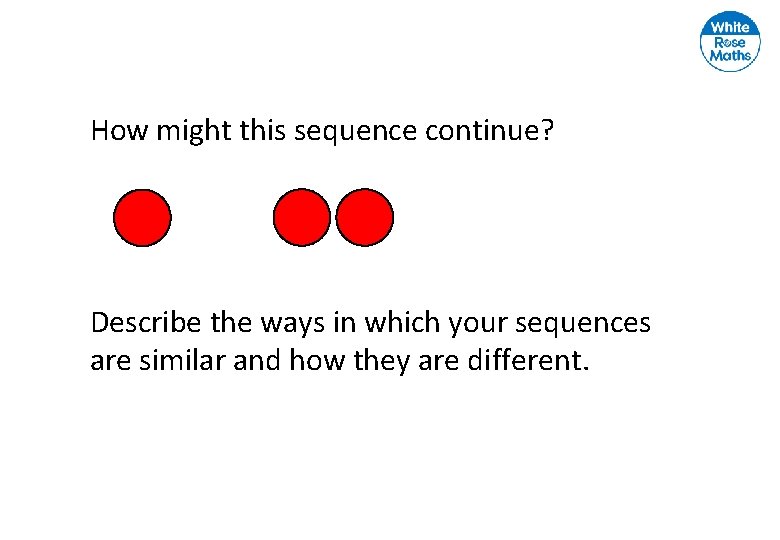
How might this sequence continue? Describe the ways in which your sequences are similar and how they are different.

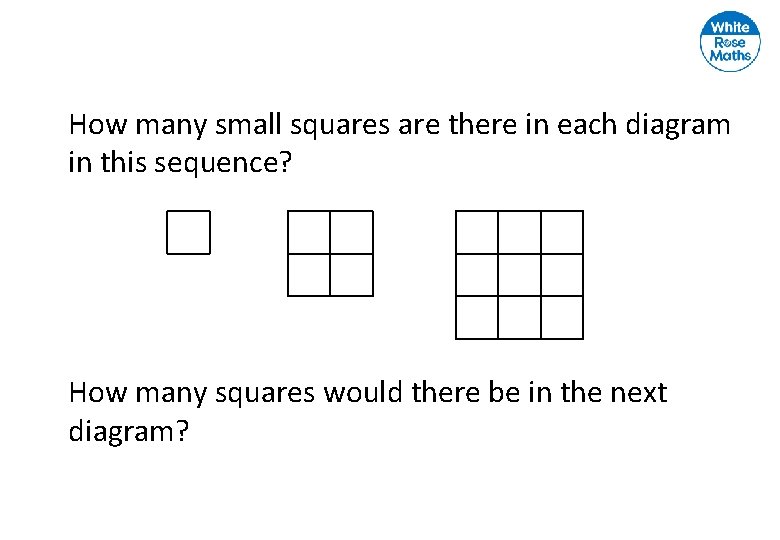
How many small squares are there in each diagram in this sequence? How many squares would there be in the next diagram?

How many orange squares will there be in the next term? How many white squares will there be in the next term? How many squares will there altogether in the next term? How do the numbers of squares change?
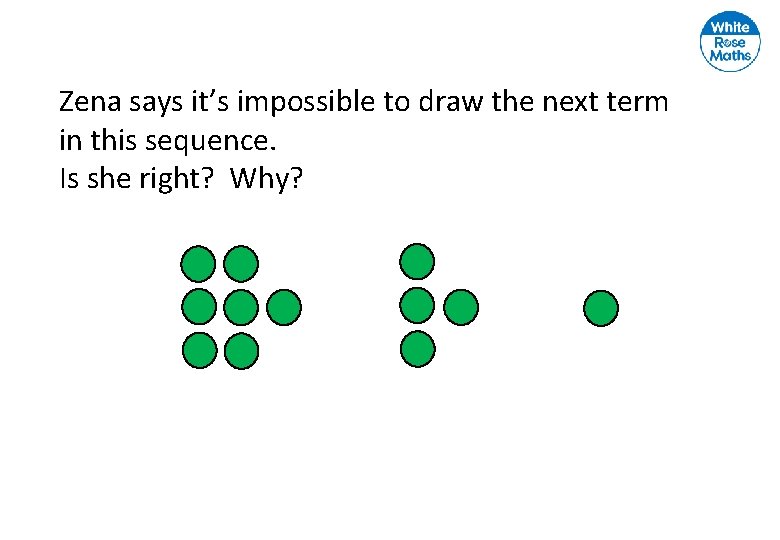
Zena says it’s impossible to draw the next term in this sequence. Is she right? Why?

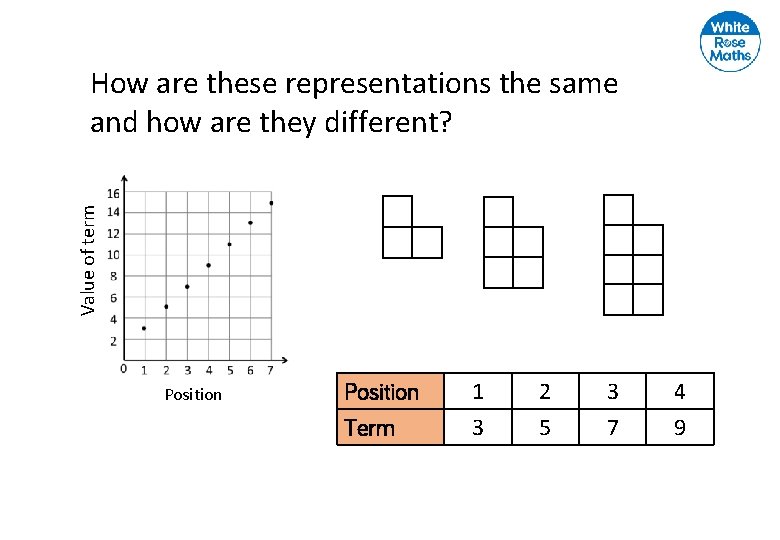
Value of term How are these representations the same and how are they different? Position Term 1 3 2 5 3 7 4 9

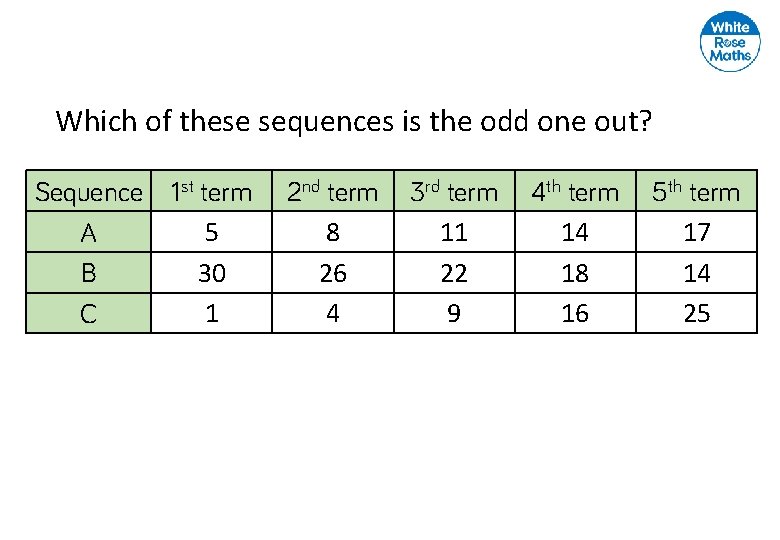
Which of these sequences is the odd one out? Sequence 1 st term 5 A 30 B 1 C 2 nd term 8 26 4 3 rd term 11 22 9 4 th term 14 18 16 5 th term 17 14 25

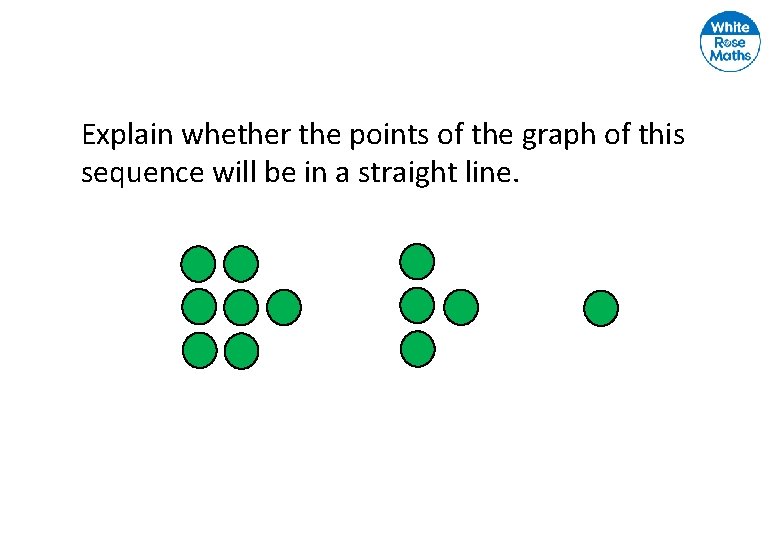
Explain whether the points of the graph of this sequence will be in a straight line.

Which of these sequences are linear, and which are not? 10 , 20 , 30 , 40 , 50… 10 , 1000 , 100 000… 90 , 85 , 80 , 75 , 70… 2 , 3 , 5 , 8 , 12… 1 , 2 , 3 , 5 , 8 , 13….
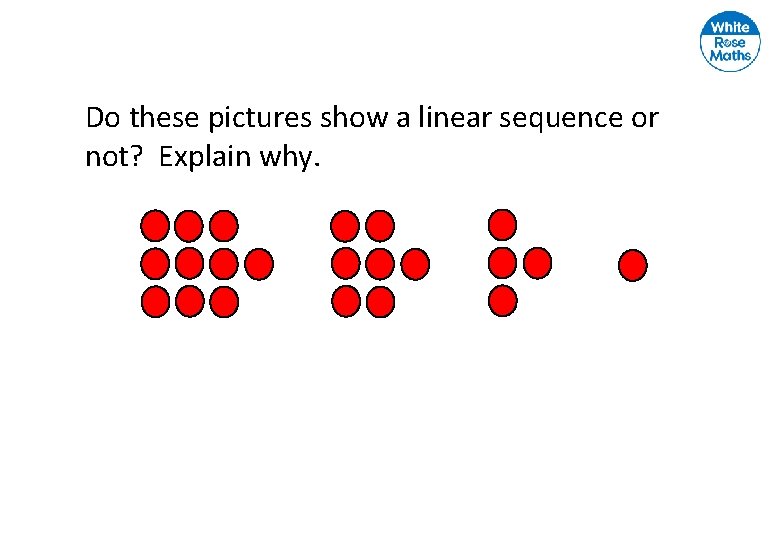
Do these pictures show a linear sequence or not? Explain why.

Jack says this sequence is linear because there is a constant difference of one between the terms. Is he right? 1 , 2 , 1 , 2…

Find the next three terms in each of the following linear sequences. 60 , 74 , 88 , ____ 8000 , 11 000, 14 000 , ____ 90 , 85 , 80 , ____ 0. 9 , 1. 2 , 1. 5 , ____ 7. 42, 6. 81 , ____

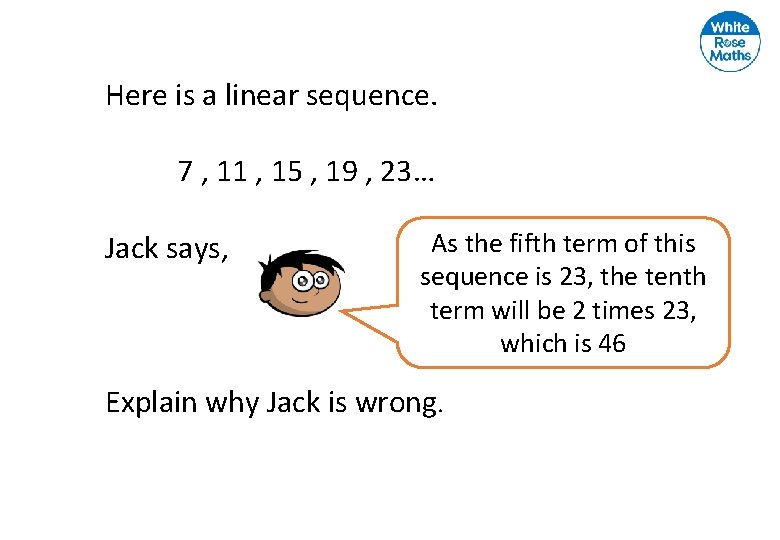
Here is a linear sequence. 7 , 11 , 15 , 19 , 23… Jack says, As the fifth term of this sequence is 23, the tenth term will be 2 times 23, which is 46 Explain why Jack is wrong.

How many linear sequences can you create starting with 90 , 88…?

An ascending linear sequence starts with 4. 7 and has common difference 2. 5. Find the first six terms of the sequence. What do you notice about all the numbers in the sequence? Create an integer linear sequence whose last digits are always a repeating series.

Find the next two terms in each of the following sequences. 1 , 2 , 4 , 8 , ____ 64 000 , 32 000, 16 000 , ____ 1 , 3 , 4 , ____ 100 , 150 , 225 , ____ 1 , 2 , 3, 5 , 8 , ____

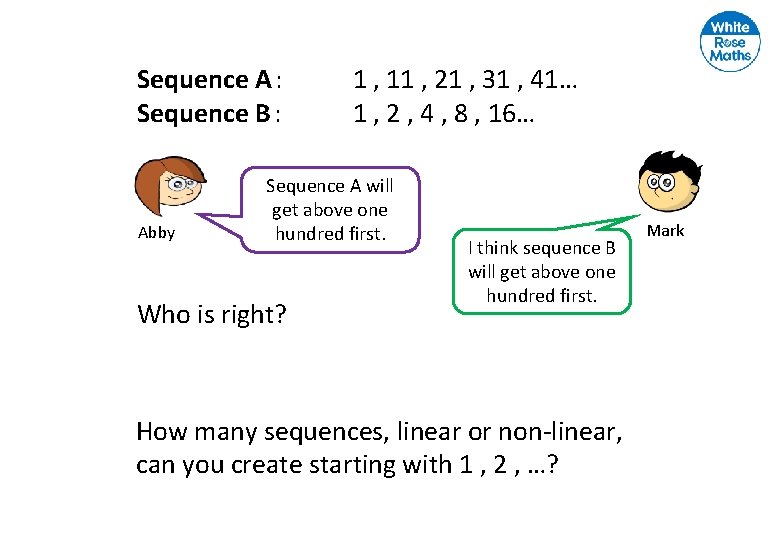
Sequence A: Sequence B : Abby 1 , 11 , 21 , 31 , 41… 1 , 2 , 4 , 8 , 16… Sequence A will get above one hundred first. Who is right? I think sequence B will get above one hundred first. How many sequences, linear or non-linear, can you create starting with 1 , 2 , …? Mark

A sequence starts with the number 17. The next number is found by doubling the previous number and adding 3. Find the first five terms of the sequence. What do you notice? Create a geometric sequence whose last digits are always 6

Describe in words how these sequences change from one term to the next: 1 , 2 , 3 , 6 , ____ 64 000 , 32 000, 16 000 , ____ 8 , 24 , 72 , ____ 100 , 150 , 225 , ____ 1 , 2 , 3, 5 , 8 , ____

Describe in words how these sequences change from one term to the next: 1 , 2 , 3 , 6 , ____ 64 000 , 32 000, 16 000 , ____ 8 , 24 , 72 , ____ 100 , 150 , 225 , ____ 1 , 2 , 3, 5 , 8 , ____

The term-to-term rule of a sequence is: The next term is found by tripling the previous term. Why can’t we write out this sequence?

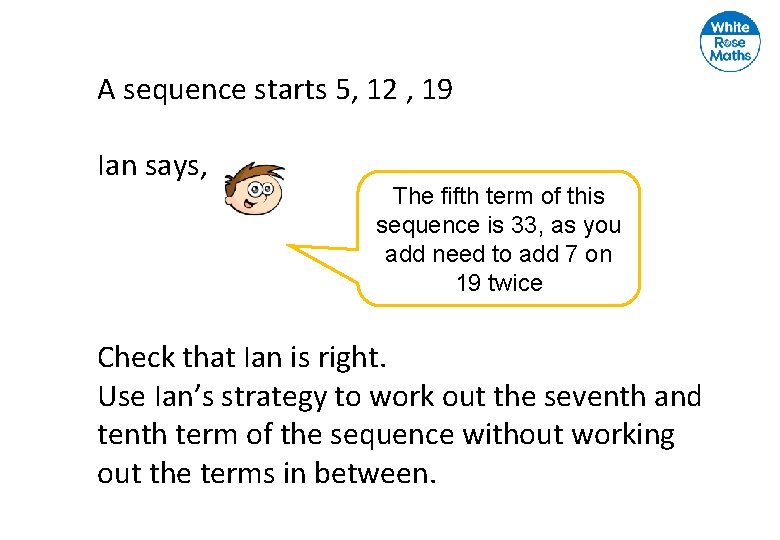
A sequence starts 5, 12 , 19 Ian says, The fifth term of this sequence is 33, as you add need to add 7 on 19 twice Check that Ian is right. Use Ian’s strategy to work out the seventh and tenth term of the sequence without working out the terms in between.

Find the missing terms in each of these sequences: 2 , 8 , ____ 2 , ____ , 8 2 , _____, 8 6 , ____ , 14 , ____ , 22, ____ 8000 , ________ , 6500, _______

The first term of a sequence is 4 and the third term is 16 If the sequence is arithmetic, what are the second and fourth terms? If the sequence is geometric, what are the second and fourth terms? Can you find rules for other sequences that start 4 , ____ , 16?

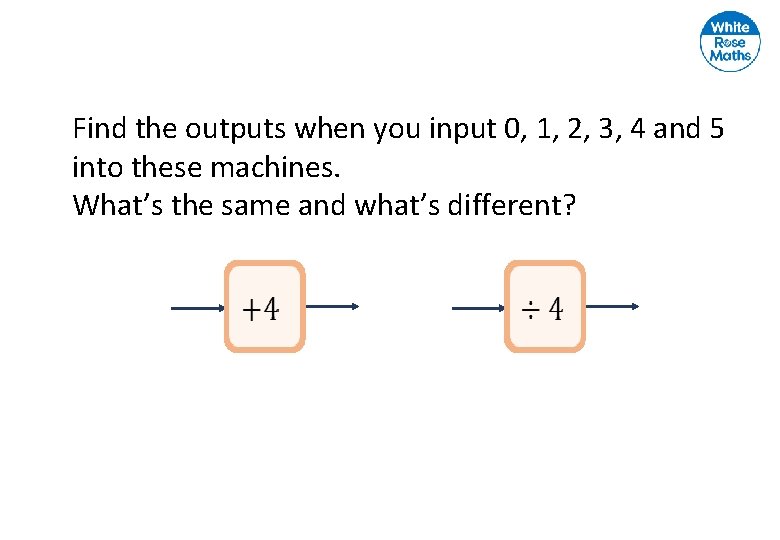
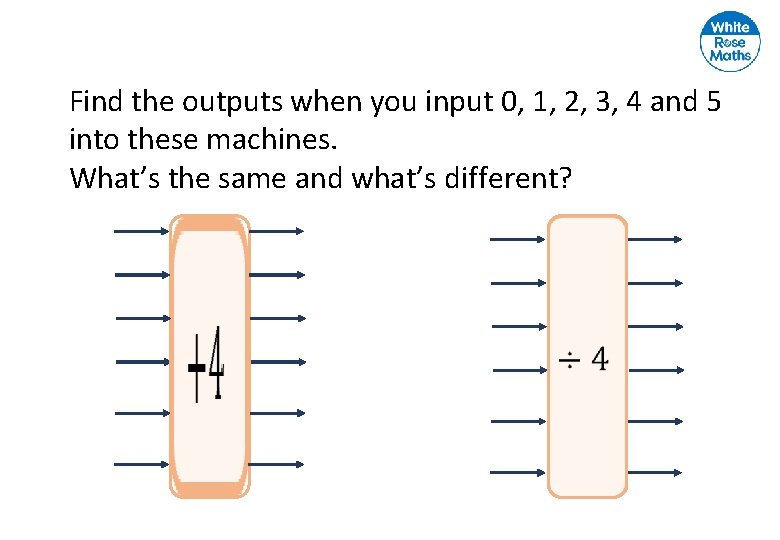
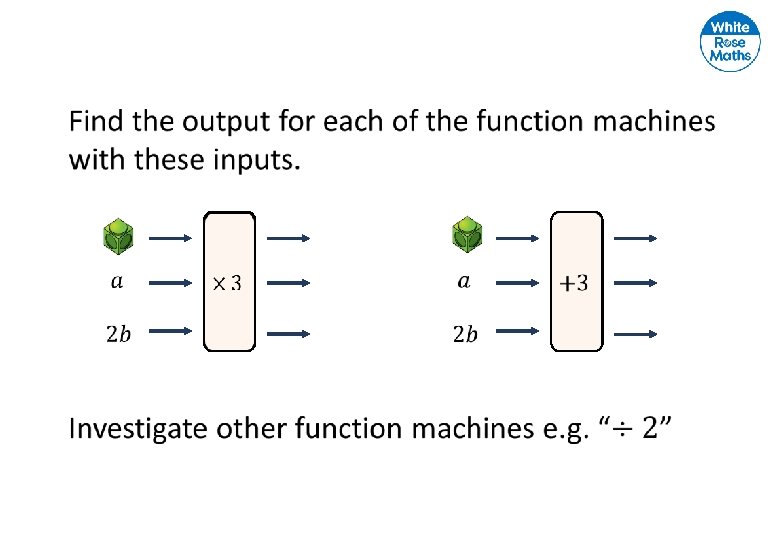
Find the outputs when you input 0, 1, 2, 3, 4 and 5 into these machines. What’s the same and what’s different?

Find the outputs when you input 0, 1, 2, 3, 4 and 5 into these machines. What’s the same and what’s different?

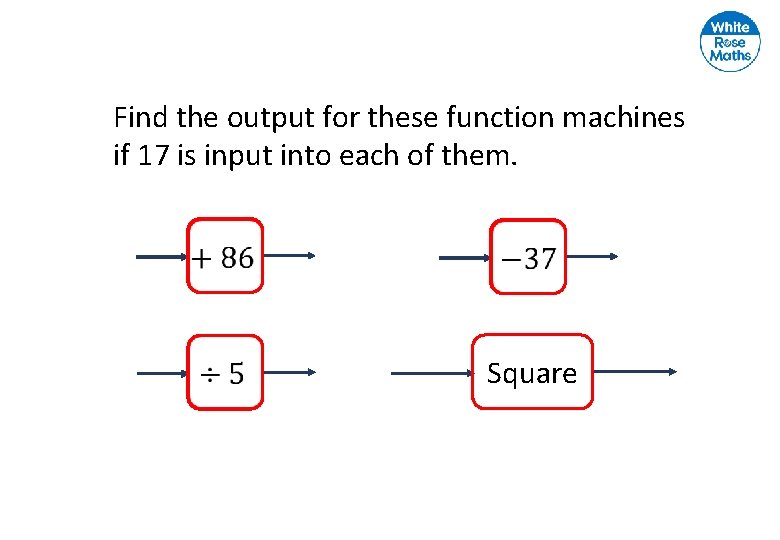
Find the output for these function machines if 17 is input into each of them. Square

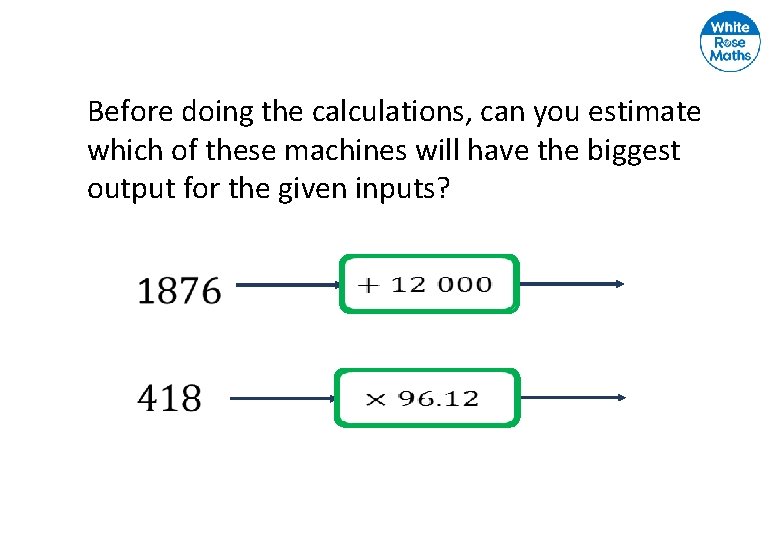
Before doing the calculations, can you estimate which of these machines will have the biggest output for the given inputs?

How many functions can you think of where the output is always the same as the input?

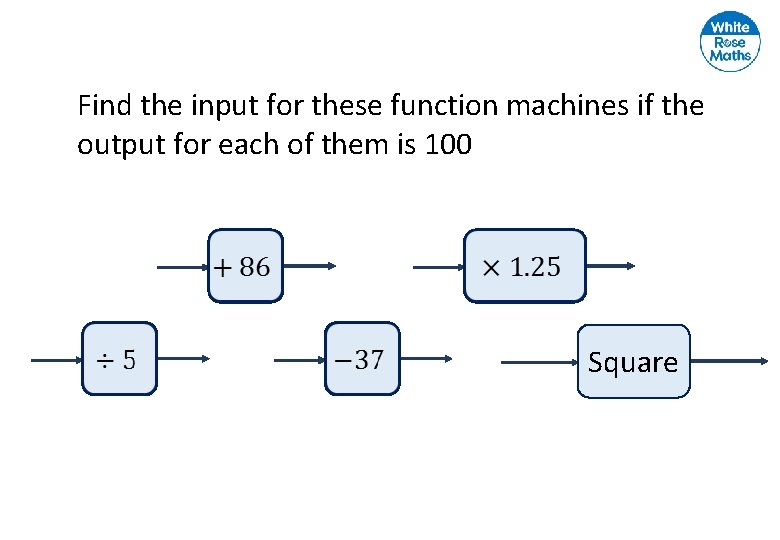
Find the input for these function machines if the output for each of them is 100 Square

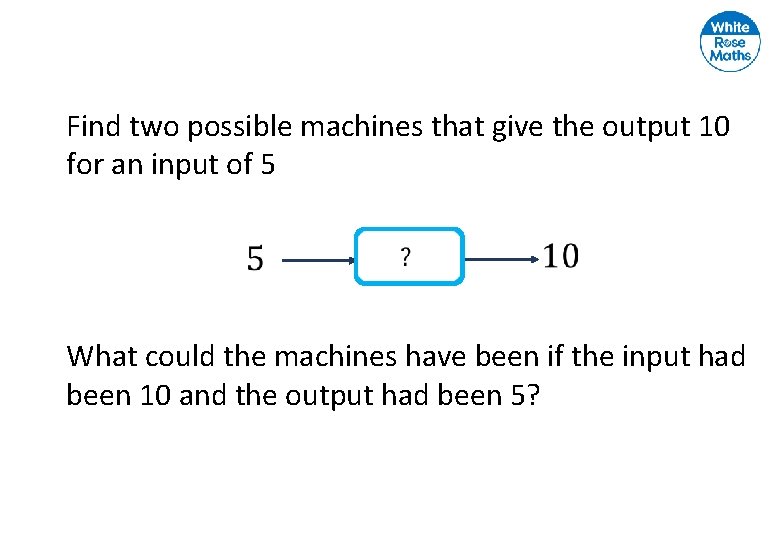
Find two possible machines that give the output 10 for an input of 5 What could the machines have been if the input had been 10 and the output had been 5?

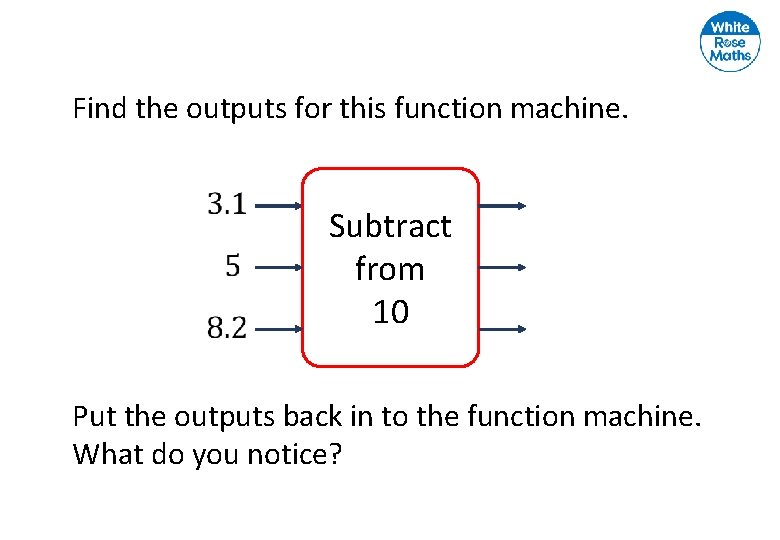
Find the outputs for this function machine. Subtract from 10 Put the outputs back in to the function machine. What do you notice?

Investigate inverse functions on your calculator.

How are these sets of calculations the same and how are they different?




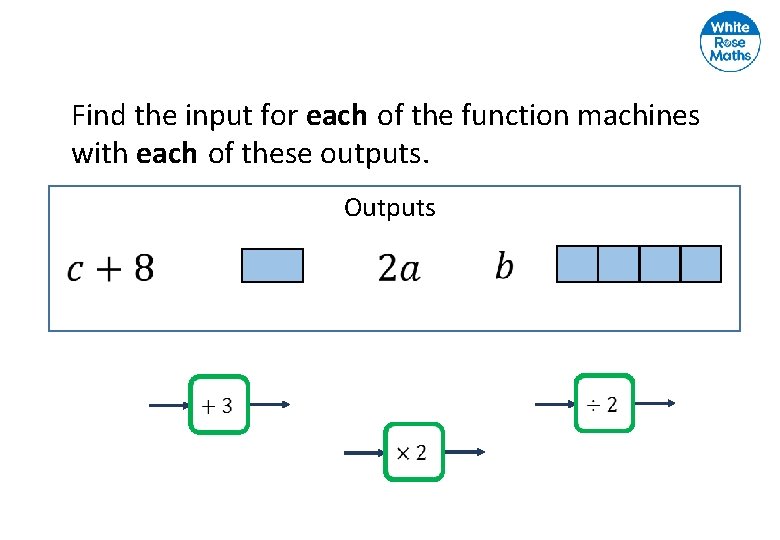
Find the input for each of the function machines with each of these outputs. Outputs

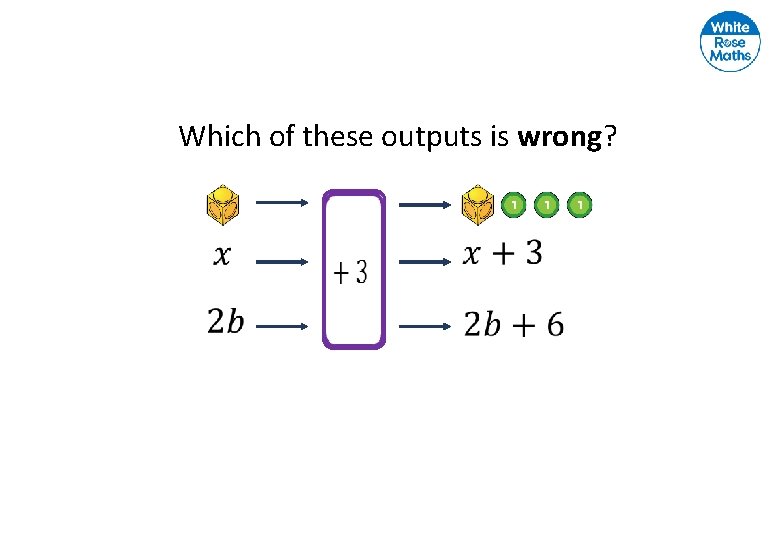
Which of these outputs is wrong?

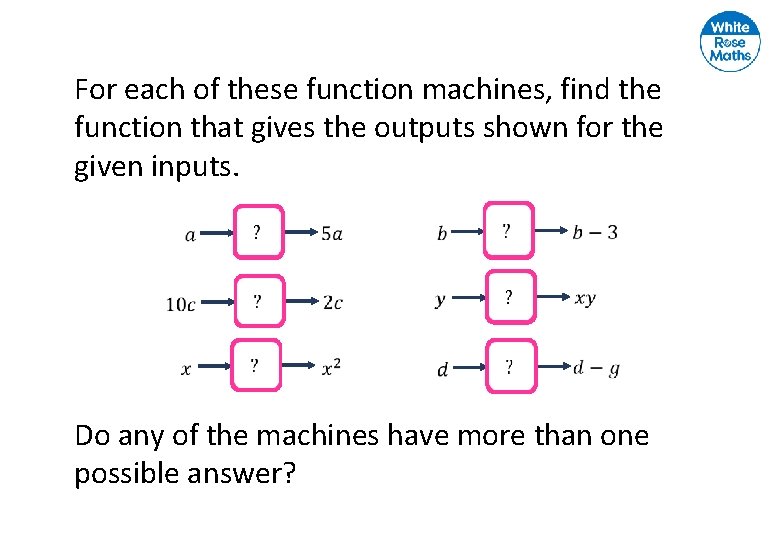
For each of these function machines, find the function that gives the outputs shown for the given inputs. Do any of the machines have more than one possible answer?

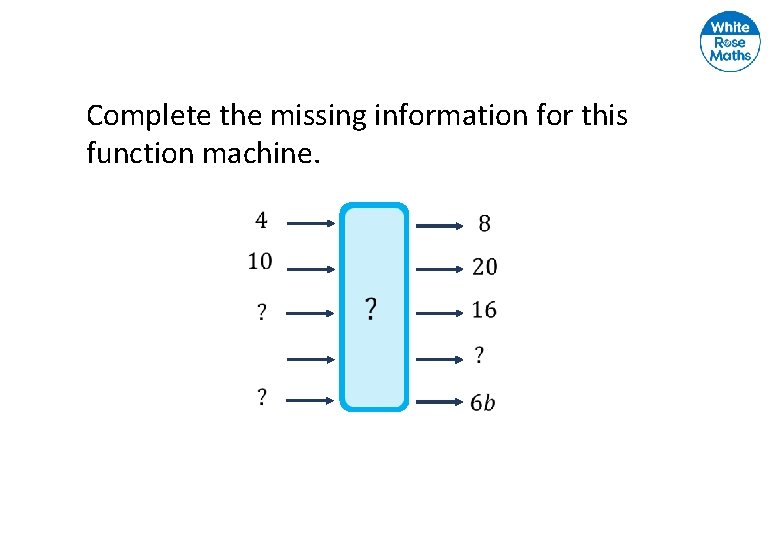
Complete the missing information for this function machine.




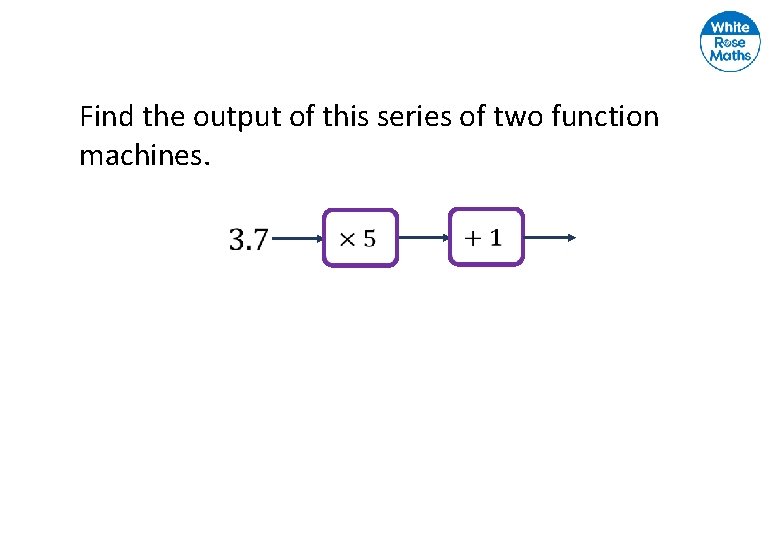
Find the output of this series of two function machines.

I think of a number, double it and then add on 9 The result is 22. 4 Show this using a series of function machines. Use inverse operations to work out the number I started with.

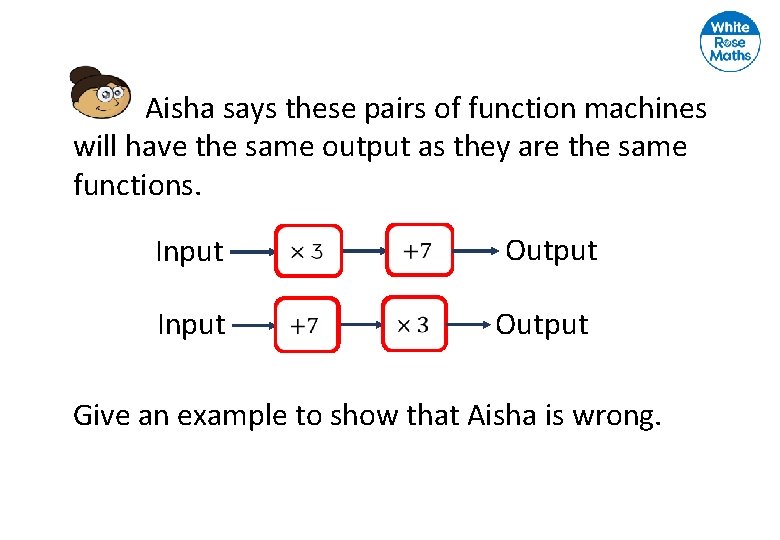
Aisha says these pairs of function machines will have the same output as they are the same functions. Input Output Give an example to show that Aisha is wrong.

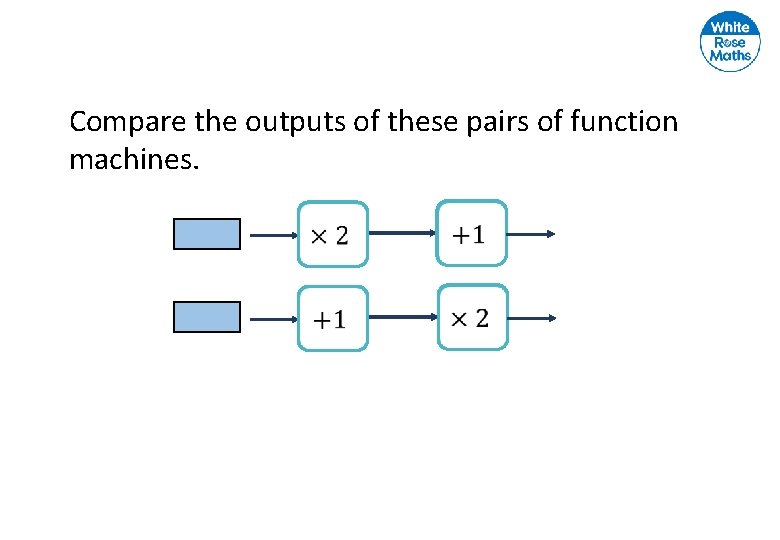
Compare the outputs of these pairs of function machines.

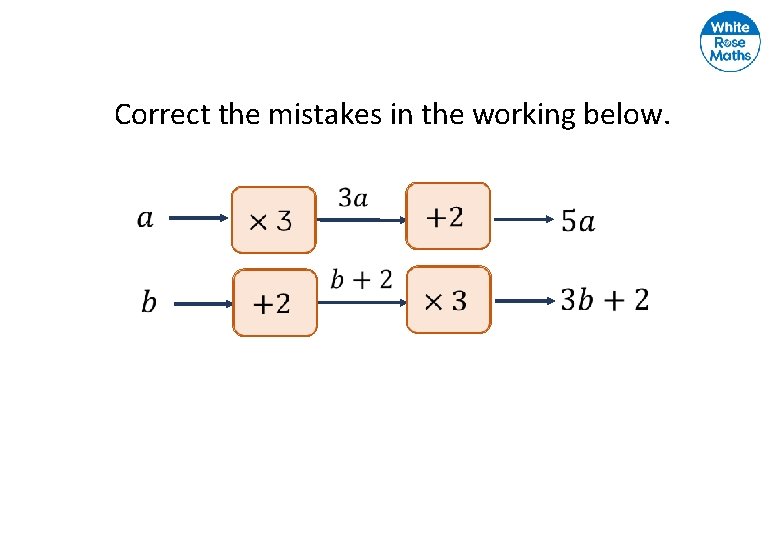
Correct the mistakes in the working below.

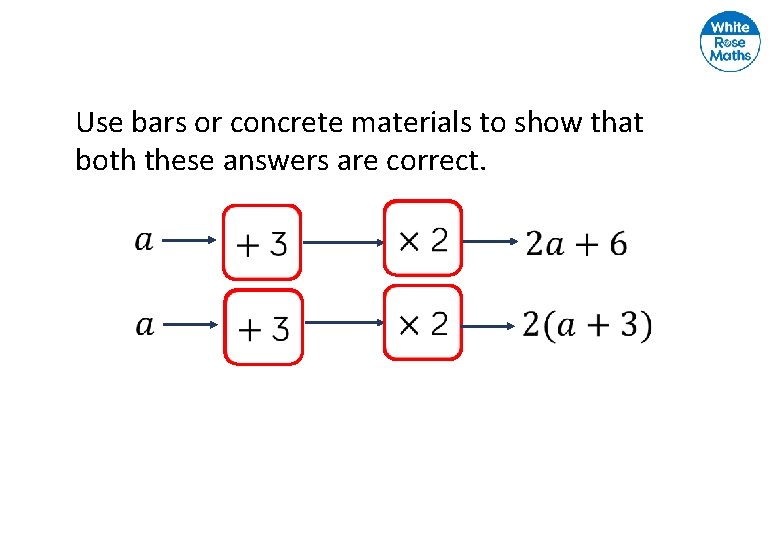
Use bars or concrete materials to show that both these answers are correct.

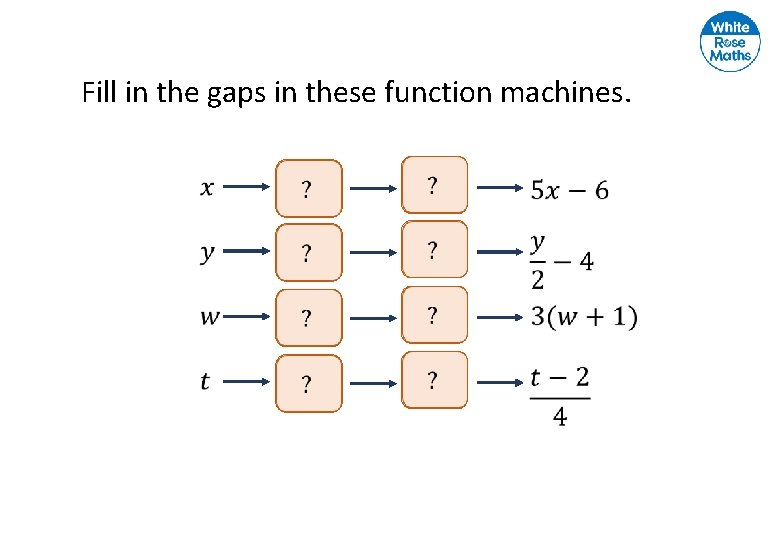
Fill in the gaps in these function machines.

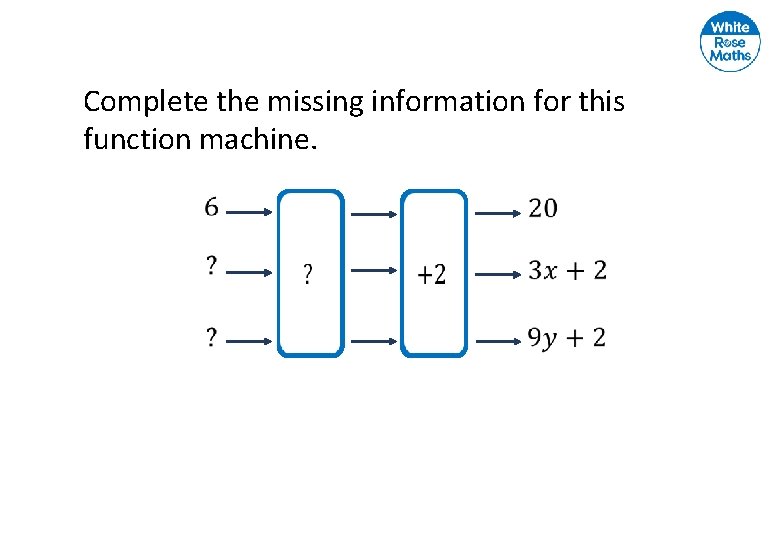
Complete the missing information for this function machine.

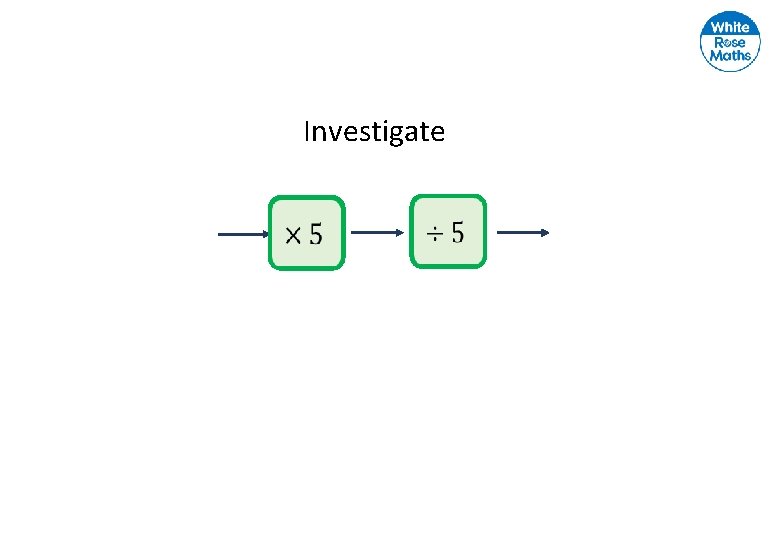
Investigate











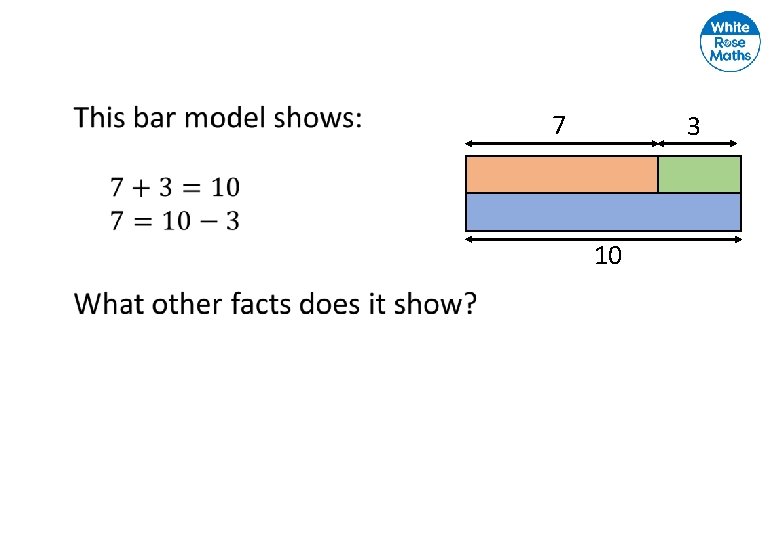
7 3 10

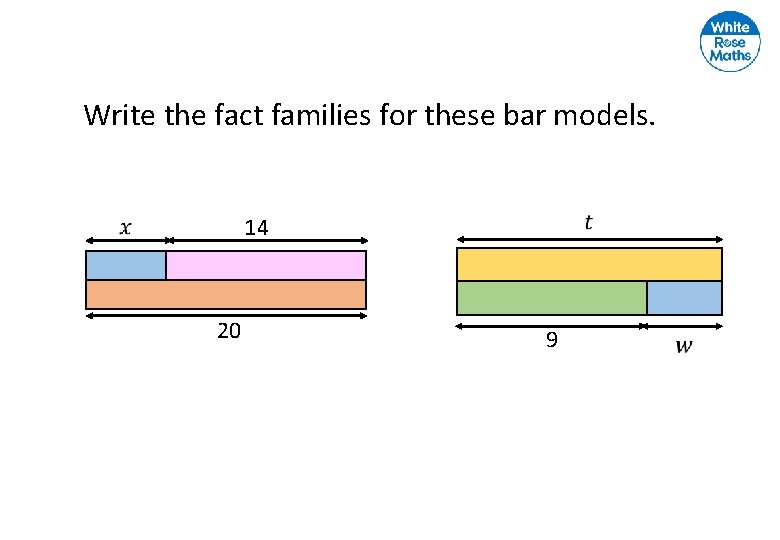
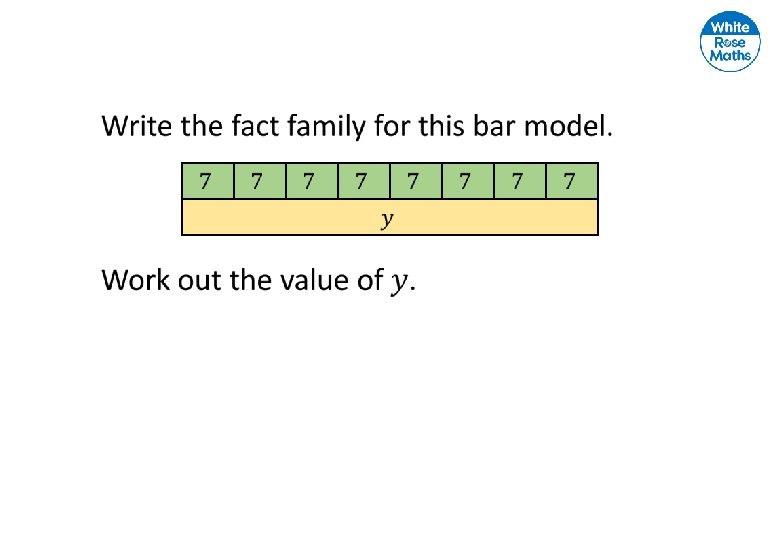
Write the fact families for these bar models. 14 20 9

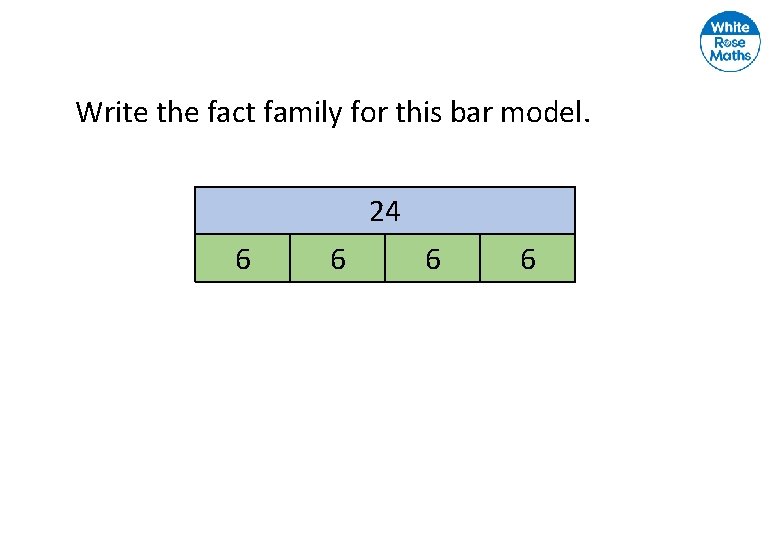
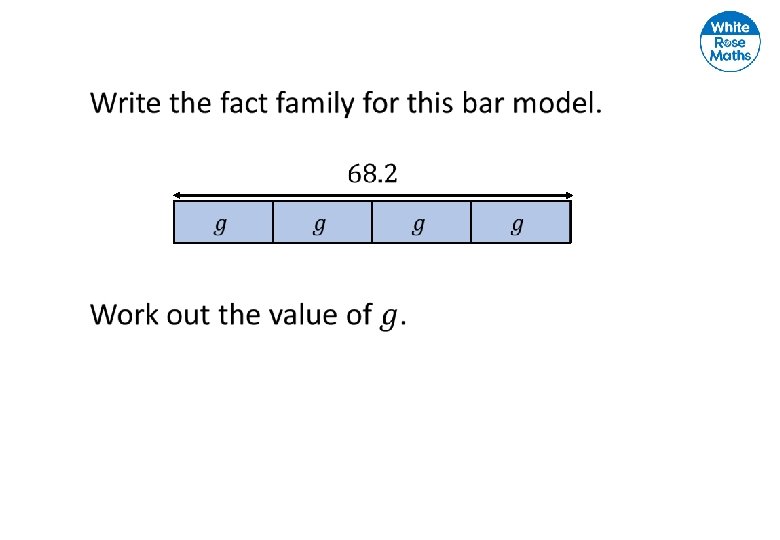
Write the fact family for this bar model. 24 6 6





Ken thinks of a number. He subtracts 78 from his number and gets the answer 137 Show this information as an equation and solve the equation to find Ken’s number. How else could you represent the information?



Marta thinks of a number. She divides her number by 7 and gets the answer 42 Write this information as an equation. Solve your equation to find Marta’s number.

Like terms Unlike terms Explain why the terms in the left are called ‘like terms’ and the terms on the right are called ‘unlike terms’.