DRAFT Version 1 A Microscopic picture of scission

DRAFT Version 1 A Microscopic picture of scission March 15, 2010 Walid Younes Lawrence Livermore National Laboratory This work was performed under the auspices of the U. S. Department of Energy by Lawrence Livermore National Security, LLC, Lawrence Livermore National Laboratory under Contract DE-AC 52 -07 NA 27344.

Outline 1. Context for a microscopic theory of fission 2. Approaching scission 3. The nucleus near scission 2

Overview of LLNL program § Goal: predict fission-fragments properties (energies, shapes, yields) as a function of incident energy § Two complementary approaches Fully-mic = HFB+TDGCM (more predictive, less acc) Many-body theory Informs/guides Fragment properties Fission-neutron spectrum Fission chain yields Mic+Stat. mech (more acc, less predictive) • Common to both: what is the microscopic picture of scission? Crucial to understanding the entire fission process Crucial to the extraction of realistic fragments properties 3

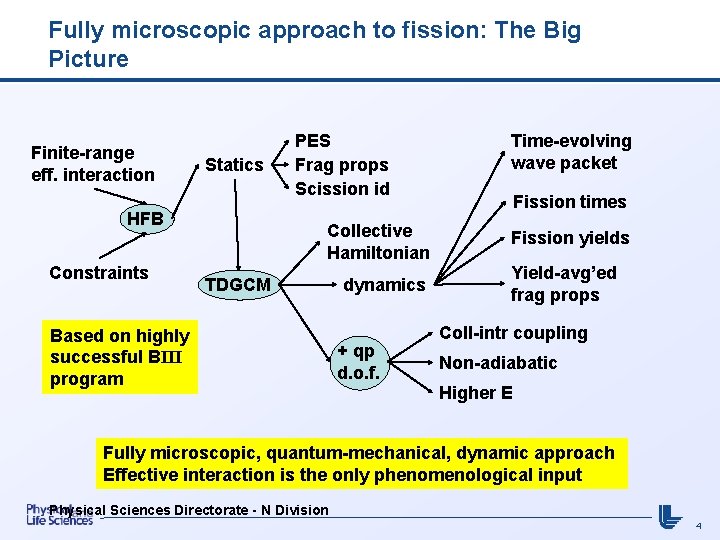
Fully microscopic approach to fission: The Big Picture Finite-range eff. interaction Statics HFB Constraints PES Frag props Scission id Collective Hamiltonian TDGCM Based on highly successful BIII program dynamics + qp d. o. f. Time-evolving wave packet Fission times Fission yields Yield-avg’ed frag props Coll-intr coupling Non-adiabatic Higher E Fully microscopic, quantum-mechanical, dynamic approach Effective interaction is the only phenomenological input Physical Sciences Directorate - N Division 4

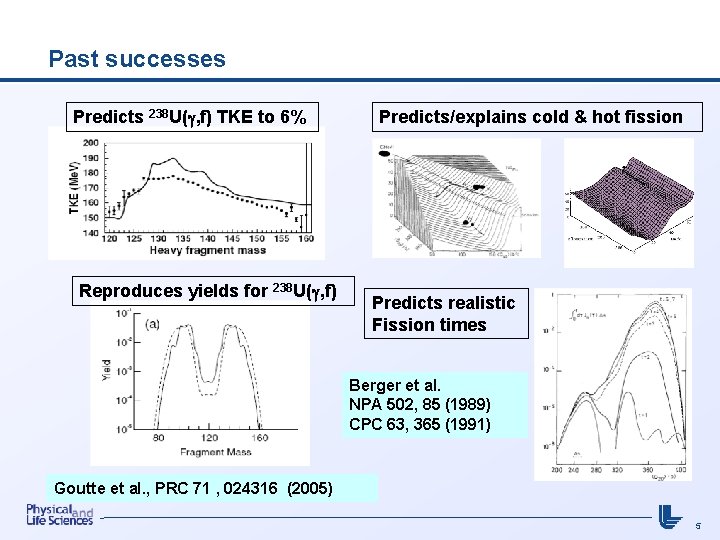
Past successes Predicts 238 U( , f) TKE to 6% Reproduces yields for 238 U( , f) Predicts/explains cold & hot fission Predicts realistic Fission times Berger et al. NPA 502, 85 (1989) CPC 63, 365 (1991) Goutte et al. , PRC 71 , 024316 (2005) 5

Approaching scission § What are the relevant degrees of freedom near scission § Discontinuities along the path to scission? 6

Fission and the role of collective coordinates: Q 20 and Q 30 240 Pu Most probable path 7

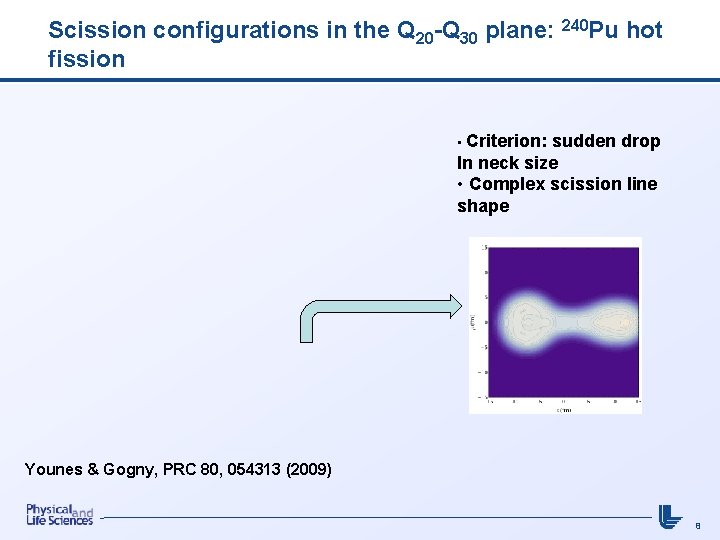
Scission configurations in the Q 20 -Q 30 plane: 240 Pu hot fission • Criterion: sudden drop In neck size • Complex scission line shape Younes & Gogny, PRC 80, 054313 (2009) 8

A more detailed view: the Q 40 collective coordinate Focus on symmetric fission Q 20 -Q 40 map for Q 30 = 0 b 3/2 • well-defined troughs • barrier between valleys 9

A more detailed view: barrier between fusion & fission in Q 20 -Q 40 240 Pu, symmetric fission • ~ 5. 6 Me. V barrier at Q 20 = 320 b, disappear gradually • exit near 300 b (cold), 580 b (hot) or anywhere in between • Berger et al. , NPA 428, 23 (1984) Physical Sciences Directorate - N Division 10

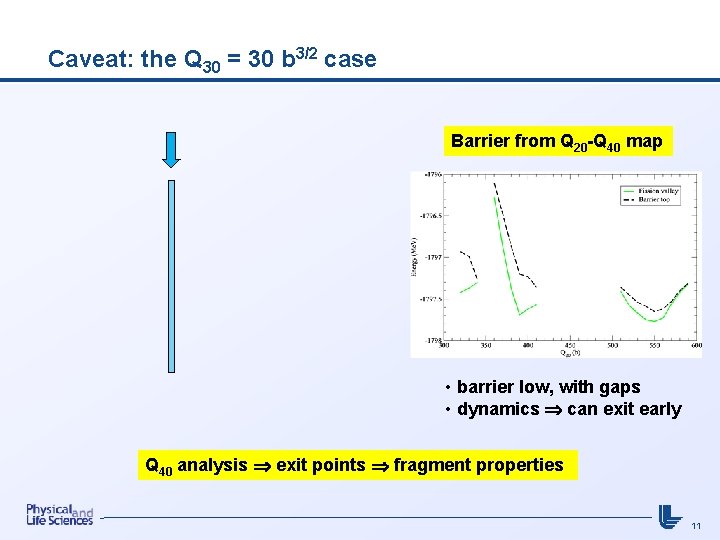
Caveat: the Q 30 = 30 b 3/2 case Barrier from Q 20 -Q 40 map • barrier low, with gaps • dynamics can exit early Q 40 analysis exit points fragment properties 11

Controlling the approach to scission: the QN coordinate 240 Pu, most prob. Q 30, hot fission Calc at discontinuity with QN 7. 6 -Me. V discontinuity Younes & Gogny, PRC 80, 054313 (2009) • discontinuity large error in fragment properties • QN ~ neck size controlled approach to scission 12

Identifying scission § How do we identify scission microscopically? § How do we identify the pre-fragments? § What are the fission-fragment properties? 13

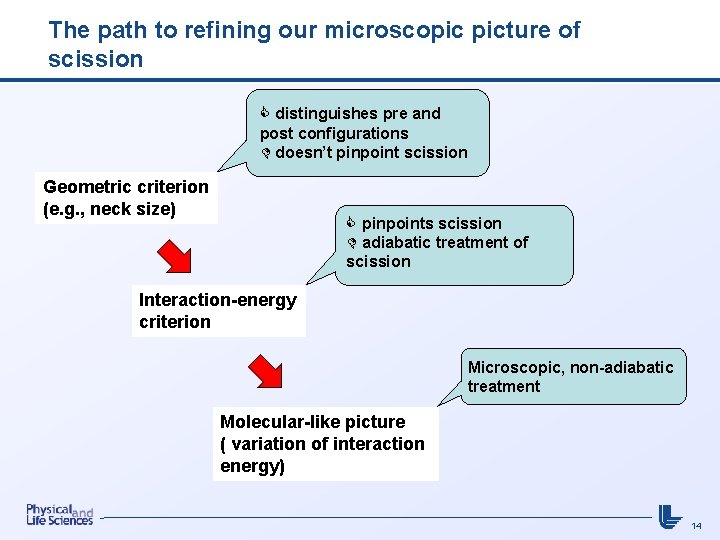
The path to refining our microscopic picture of scission distinguishes pre and post configurations doesn’t pinpoint scission Geometric criterion (e. g. , neck size) pinpoints scission adiabatic treatment of scission Interaction-energy criterion Microscopic, non-adiabatic treatment Molecular-like picture ( variation of interaction energy) 14

Energy-based criterion for identifying the scission configuration § Idea: scission occurs as soon as there is enough energy in system to overcome attractive interaction between fragments • Use neck size (QN) as constraint to approach scission • Identify s. p. wavefunctions for left and right fragments tot 1 + 2 12, with 12 0 at large separation • Calculate Eint = EHFB-EHFB(L)-EHFB(R)-Ecoul • Work in representation that minimizes fragment tails E • Scission occurs as soon as Eint = E • Scission can occur with QN 0 • Caveats: • simplified 1 D picture • multi-dim fission smaller E available (Berger et al. , NPA 428, 23 (1984)) Younes & Gogny, AIP proceedings 1175, 3 (2009)/ar. Xiv: 0910. 1804 v 1 15

Identifying the pre-fragments: choice of representation QN = 0. 01 • HFB solution defined up to unitary trans • Free to choose representation • Arbitrary rep can lead to large frag tails • With microscopic def of fragments, we see the tails • Tail-minimizing rep (via orthogonal transformation of s. p. wave funcs) • produces reasonable Eint 16

Choosing a representation that minimizes tails § Define localization parameter 1 for completely localized qp 0 for completely unlocalized qp • For a pair of states: § Identify pairs of states (i, j) and angle such that • Gives 17

Tail reduction at scission: Q 20 = 365 b, Q 30 = 60 b 3/2, QN = 1. 55 Before wave function localization After wave function localization Operation does not affect total energy, but allows • identication of left and right pre-fragments • definition of a separation distance • calculation of interaction energy 18

19 Remarkable results for a parameterless calculation! Younes & Gogny, AIP proceedings 1175, 3 (2009)/ar. Xiv: 0910. 1804 v 1 Results: comparison with observables for 239 Pu(nth, f)

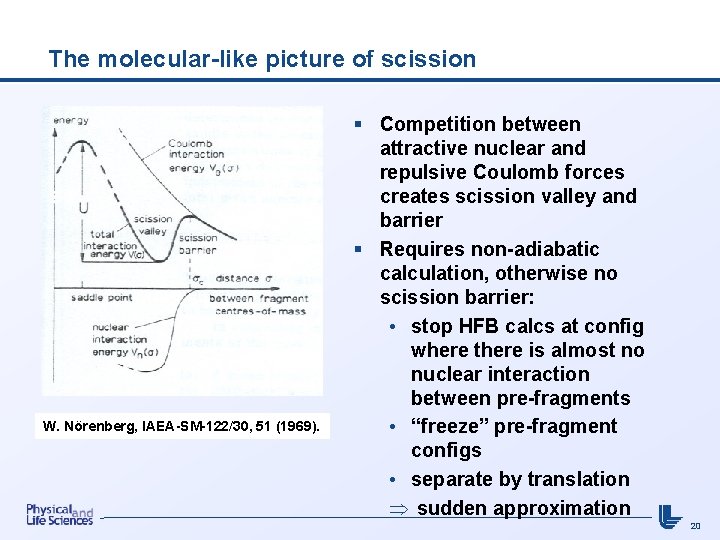
The molecular-like picture of scission W. Nörenberg, IAEA-SM-122/30, 51 (1969). § Competition between attractive nuclear and repulsive Coulomb forces creates scission valley and barrier § Requires non-adiabatic calculation, otherwise no scission barrier: • stop HFB calcs at config where there is almost no nuclear interaction between pre-fragments • “freeze” pre-fragment configs • separate by translation Þ sudden approximation 20

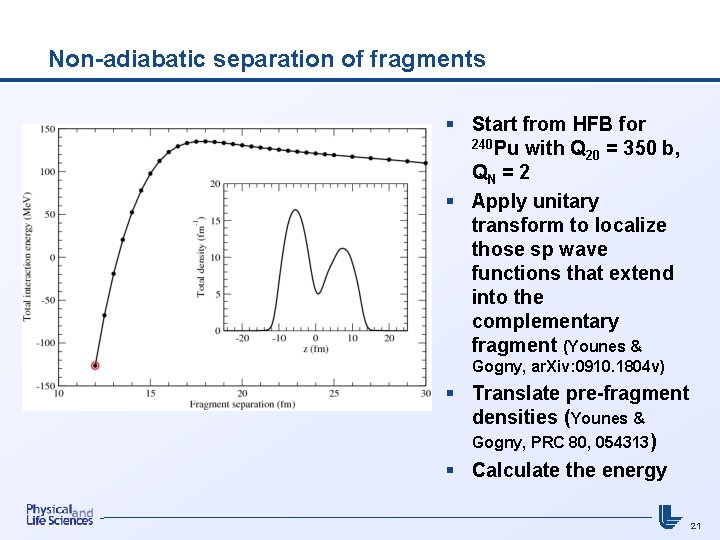
Non-adiabatic separation of fragments § Start from HFB for 240 Pu with Q 20 = 350 b, QN = 2 § Apply unitary transform to localize those sp wave functions that extend into the complementary fragment (Younes & Gogny, ar. Xiv: 0910. 1804 v) § Translate pre-fragment densities (Younes & Gogny, PRC 80, 054313) § Calculate the energy 21

The molecular-like microscopic picture of scission § Sharp drop at Q 20 = 370 b for adiabatic calc (hot fission) § Non-adiabatic calcs for different starting Q 20, QN • • Scission barrier decreases with Q 20 and QN For hot fission, scission barrier disappears between QN = 1 and 2 § This is still a static picture § TDGCM dynamics • • Pre-scission energy available to overcome scission barrier Some of that energy may be taken up by collective 22

Application: microscopic Wilkins model for mass yields § Based on Wilkins et al. , PRC 14, 1832 (1976). (See also S. Heinrich thesis) § Static microscopic calcs of fragments at many deformations ZH, AH, b, Tint d ZL, AL, b, Tint Tcoll § Calculate energy of two-fragment system as a function of separation d § Identify distance d at scission such that § Boltzmann factor gives probability distributions: exp(-Etot/Tcoll) 23

The semi-microscopic approach: Mass yields 236 U(n th, f) using LDM (Wilkins et al. , 1976) 239 Pu(n th, f) using microscopic theory (Our work, in progress…) Already better than LDM. Should improve with: • proper treatment of anti-symmetrization • more fragments included • intrinsic temperature • revisit Pauli blocking in odd-A and odd-odd nuclei 24

Conclusions § Quantitative, microscopic picture of scission is essential for a predictive theory of fission § Near scission, new collective d. o. f. become relevant (QN, d) § Molecular-like picture of fission provides solid framework to understand scission • Requires the identification of left and right pre-fragments and their interaction energy • Microscopic definition of scission • Sudden approximation at scission • Non-adiabatic separation of the fragments 25

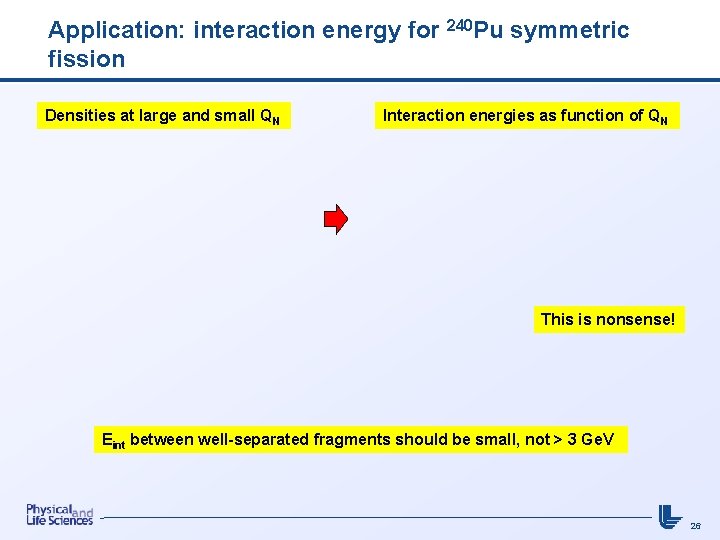
Application: interaction energy for 240 Pu symmetric fission Densities at large and small QN Interaction energies as function of QN This is nonsense! Eint between well-separated fragments should be small, not > 3 Ge. V 26

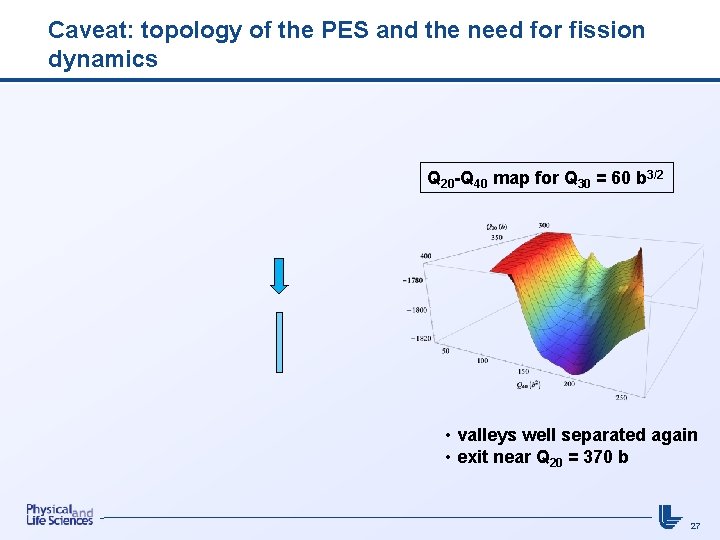
Caveat: topology of the PES and the need for fission dynamics Q 20 -Q 40 map for Q 30 = 60 b 3/2 • valleys well separated again • exit near Q 20 = 370 b 27