DR Gatot F Hertono MSc Design and Analysis

DR. Gatot F. Hertono, MSc. Design and Analysis of ALGORITHM (Session 1)

Silabus Konsep Teori Dasar • Analisa dan Perancangan Algoritma • Kompleksitas Waktu • Notasi Asimtotik • Relasi Rekursi

Algorithms = Logic + Control Problem: searching specific data in a database Logic: the way to find the specific data Control: finding the efficient way

Think about this How do we find the minimum/maximum element efficiently? 88 52 14 31 25 98 30 2 62 79 3 Design Which one of these two algorithms is faster to compute? Given time complexity of Algorithm A: Analysis Algorithm B:

Definition

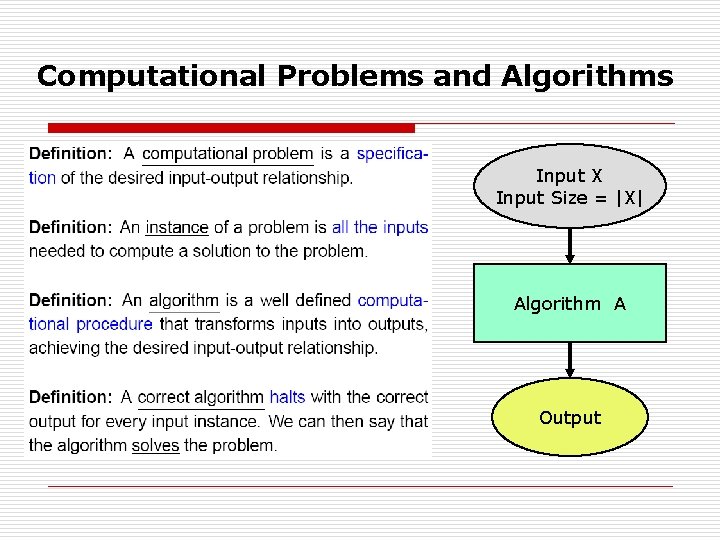
Computational Problems and Algorithms Input X Input Size = |X| Algorithm A Output

Algorithms • Design : design algorithms which minimize the cost • Analysis : predict the cost of an algorithm in terms of resources and performance Algorithmic is a systematic study to design and analysis of an efficient algorithm by using basic techniques (primitive operations).

Algorithm Analysis : why do we need it? The second demands an answer to predict how big the resources (related to the computation time) to solve the problem Example: Fibonacci numbers Trade-off: Correctness vs. Efficient

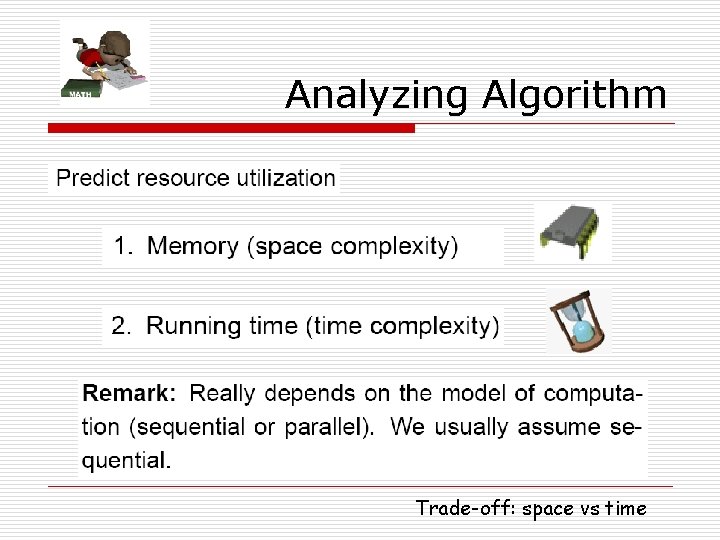
Analyzing Algorithm Trade-off: space vs time

Running time should be machine independent !! Analyzing Algorithm (continued)

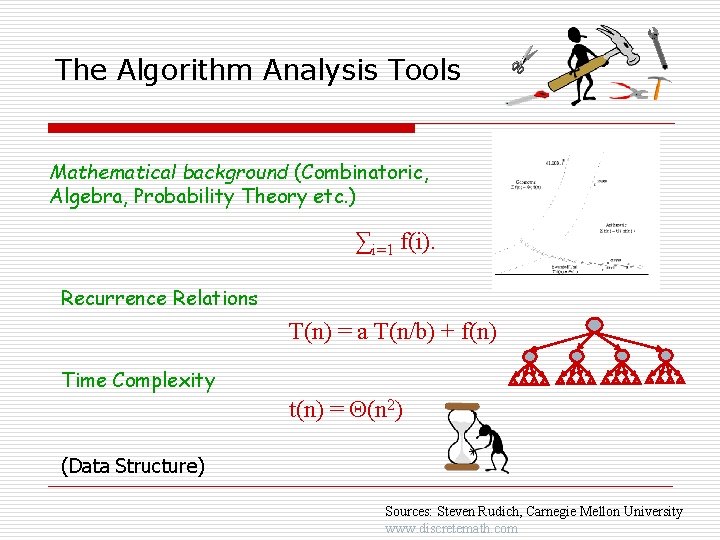
The Algorithm Analysis Tools Mathematical background (Combinatoric, Algebra, Probability Theory etc. ) ∑i=1 f(i). Recurrence Relations T(n) = a T(n/b) + f(n) Time Complexity t(n) = (n 2) (Data Structure) Sources: Steven Rudich, Carnegie Mellon University www. discretemath. com

Mathematical Background

Mathematical Background (cont. ) Floor and Ceiling

Mathematical Background Summation

Mathematical Background (cont. ) a + (a+d) + (a+2 d) + … + (a+(n-1)d) = (n(2 a+(n-1)d))/2 1+2+…+n=(n(n+1))/2 Untuk x real dan -1 < x < 1 1+x+x 2+…+xn-1=(xn-1)/(x-1) 1+2+22+…+2 n-1= 2 n-1 1+2 x+3 x 2+…+nxn-1=(nxn+1 -(n+1)xn+1)/(x-1)2 Untuk k=0, 1, 2, …, n

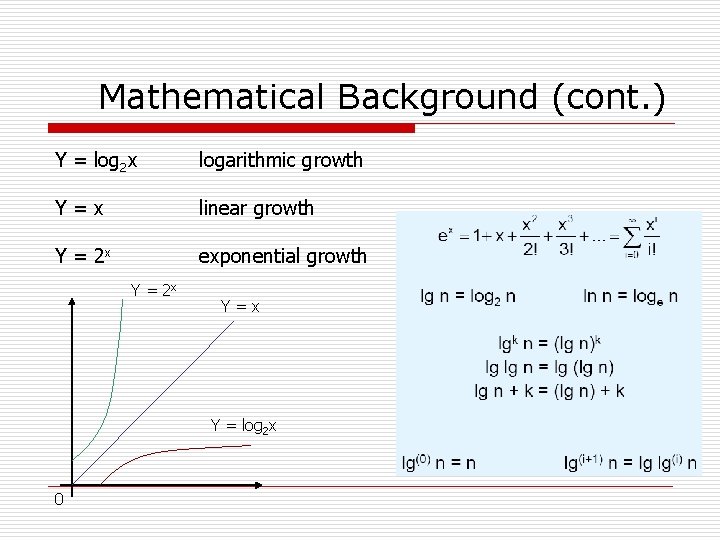
Mathematical Background (cont. ) Y = log 2 x Y = 2 x logarithmic growth linear growth exponential growth Y = x Y = log 2 x 0

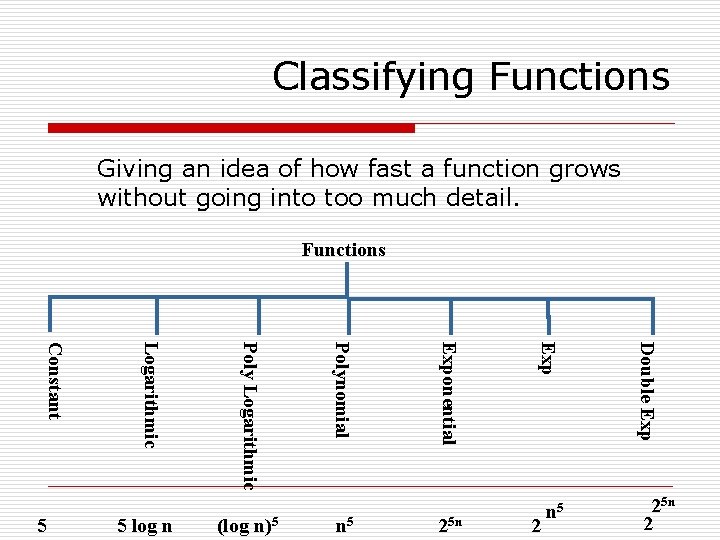
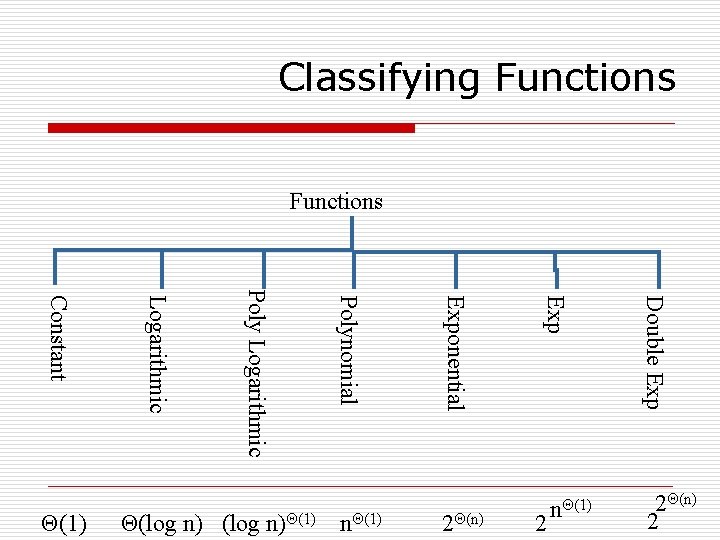
Classifying Functions Giving an idea of how fast a function grows without going into too much detail. Functions 2 Double Exp 25 n Exp n 5 Exponential (log n)5 Polynomial 5 log n Poly Logarithmic Constant 5 n 5 25 n 2

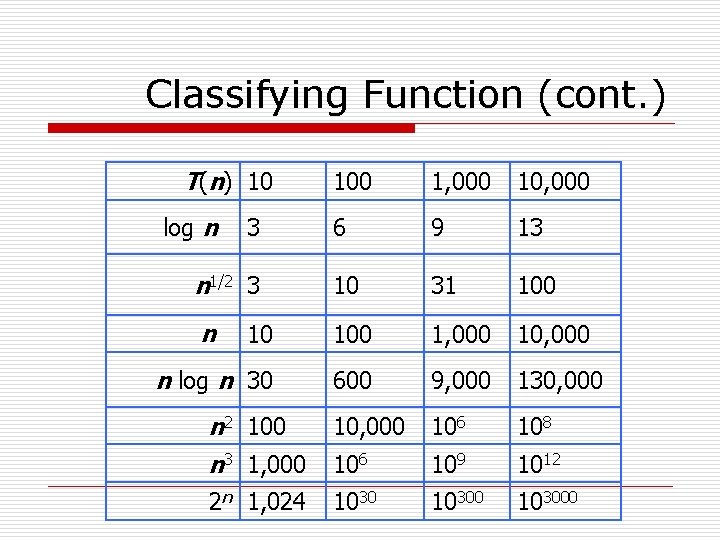
Classifying Function (cont. ) T(n) 10 100 1, 000 10, 000 6 9 13 n 1/2 3 10 31 100 n 10 100 1, 000 10, 000 n log n 30 600 9, 000 130, 000 n 2 100 n 3 1, 000 106 108 106 109 1012 2 n 1, 024 103000 log n 3

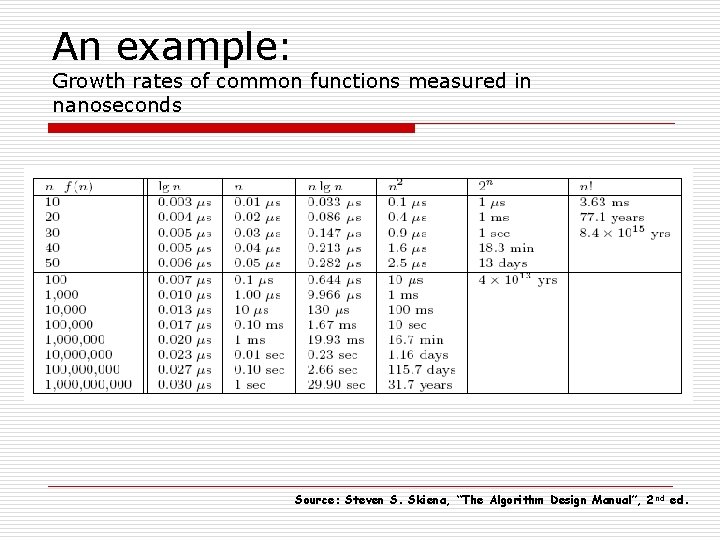
An example: Growth rates of common functions measured in nanoseconds Source: Steven S. Skiena, “The Algorithm Design Manual”, 2 nd ed.

Hints Which Functions are Quadratic? • n 2 Ignore low-order terms • 0. 001 n 2 Ignore multiplicative constants. • 1000 n 2 Ignore "small" values of n. • 5 n 2 + 3 n + 2 log n Write Θ(n 2). Which Functions are Polynomials? • nc • n 0. 0001 • n 10000 • 5 n 2 + 8 n + 2 log n • 5 n 2. 5 Ignore low-order terms Ignore power constant. Ignore "small" values of n. Write nΘ(1)

Hints (cont. ) Which Functions are Exponential? • 2 n • 20. 0001 n • 210000 n • 8 n • 2 n / n 100 • 2 n · n 100 Ignore base. Ignore constant in front of n. Ignore "small" values of n. Ignore polynomial factors. Write 2Θ(n) use Asymptotic Notation (notasi , dan O)

Classifying Functions 2 Double Exp 2Θ(n) Exp nΘ(1) Exponential Θ(log n)Θ(1) Polynomial Poly Logarithmic Constant Θ(1) nΘ(1) 2Θ(n) 2

Design of Algorithm Based on the problem type Searching Sorting Optimization Graph Numeric/Probabilistic Based on the strategic design Greedy Method Divide & Conquer Backtracking Branch & Bound Dynamic Programming Based on the computational model Sequential Parallel

Tips in Designing Algorithms 1. Formulate the problem and consider the available resources (memory and processor); 2. Identify the data abstract types that appropriate to the model of the problem (data structures); 3. Identify parts of the problem which have known algorithms and design the algorithm for the other ones; 4. Examine the correctness and analyze its performance when the algorithm design has been completed; 5. Identify a better algorithm if it exists.