Dot Product This slideshow will be a review

Dot Product This slideshow will be a review on the Dot Product of two vectors
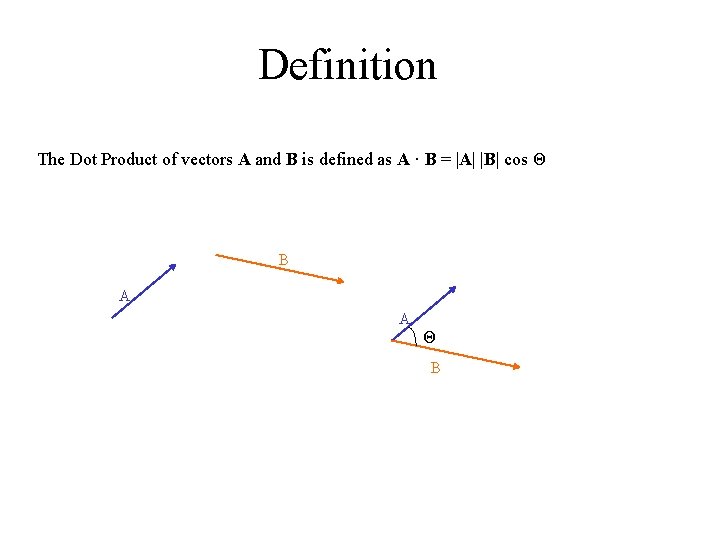
Definition The Dot Product of vectors A and B is defined as A · B = |A| |B| cos Θ B A A Θ B
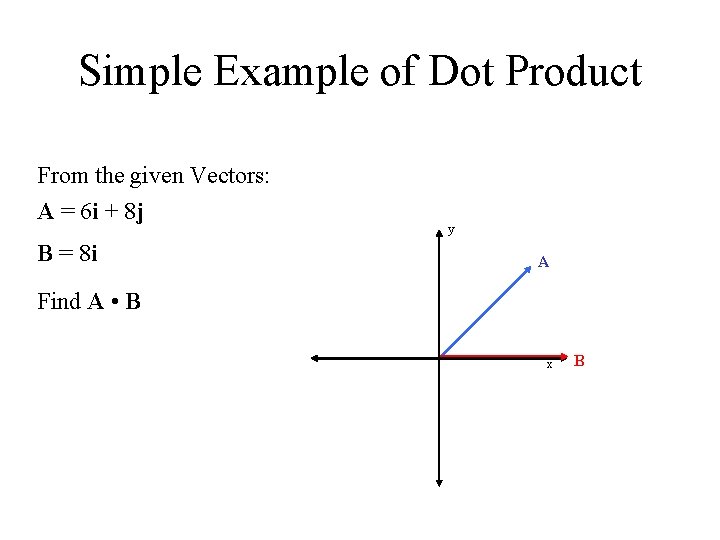
Simple Example of Dot Product From the given Vectors: A = 6 i + 8 j B = 8 i y A Find A • B x B
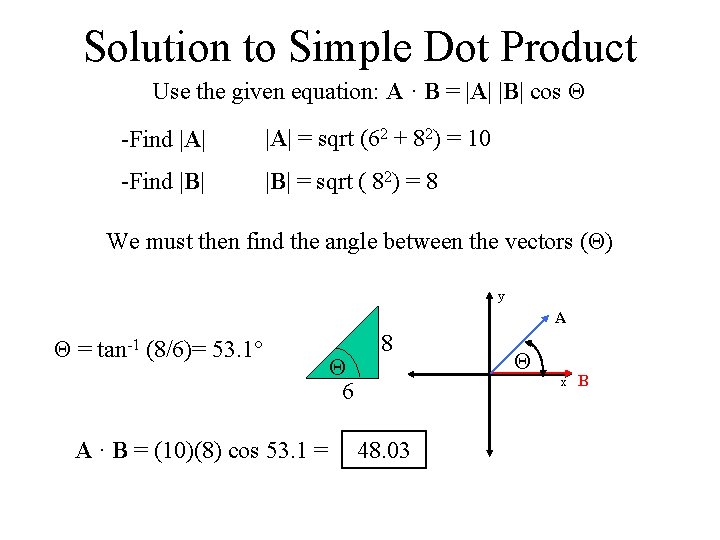
Solution to Simple Dot Product Use the given equation: A · B = |A| |B| cos Θ -Find |A| = sqrt (62 + 82) = 10 -Find |B| = sqrt ( 82) = 8 We must then find the angle between the vectors (Θ) y A Θ = tan-1 (8/6)= 53. 1° A · B = (10)(8) cos 53. 1 = Θ 6 8 Θ x 48. 03 B

Laws of Operations • Commutative A·B=B·A • Associative with respect to scalar multiplication a (A · B) = (a A) · B = A · (a B) • Distributive with respect to vector addition A · (B + D) = (A · B) + (A · D)

Dot Product Identities Since the cosine of 90° = 0, and the cosine of 0° = 1, from A · B = cos Θ, we can derive: i·i=1 j·j=1 Since the angle between two i direction vectors would be 0, the equation would be: i · i = |i| cos 0° = (1)(1)(1) = 1 k·k=1 i·j=0 j·i=0 i·k=0 k·i=0 k·j=0 j·k=0 Since the angle between two different direction vectors would be 90°, the equation would be: i · j = |i| |j| cos 90° = (1)(1)(0) = 0

Components of Dot Product Consider the dot product of two 3 dimensional vectors expressed in Cartesian vector form: A · B = (Axi + Ayj + Azk) · (Bxi + Byj + Bzk) = Ax. Bx( i · i ) + Ax. By( i · j ) + Ax. Bz( i · k ) + Ay. Bx( j · i ) + Ay. By( j · j ) + Ay. Bz( j · k ) + Ax. Bx( k · i ) + Az. By( k · j ) + Az. Bz( k · k ) Using the laws from the previous page, we see that this equation can be reduced to: A · B = Ax. Bx + Ay. By + Az. Bz Therefore, to determine the Dot Product of two vectors, multiply their corresponding x, y, z components and sum their products.
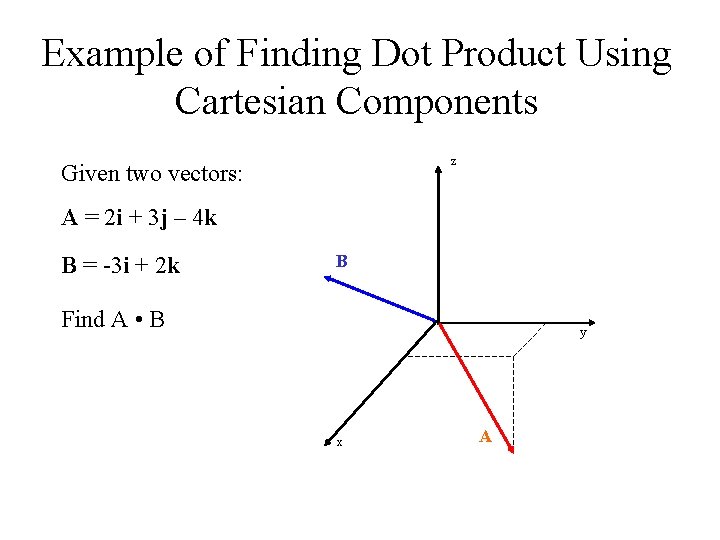
Example of Finding Dot Product Using Cartesian Components z Given two vectors: A = 2 i + 3 j – 4 k B = -3 i + 2 k B Find A • B y x A

Solution to Component Dot Product Use the formula A · B = Ax. Bx + Ay. By + Az. Bz A = 2 i + 3 j – 4 k Ax = 2; Ay = 3; Az = -4 B = -3 i + 2 k Bx = -3; By = 0; Bz = 2 A · B = (2)(-3) + (3)(0) + (-4)(2) = -14

Applications The Dot product has useful applications in mechanics 1. The angle formed between two vectors or intersecting lines The angle between the tails of vectors A and B can be determined by solving A · B = |A| |B| cos Θ, for Θ. Θ = cos -1 (A • B) |A| |B|
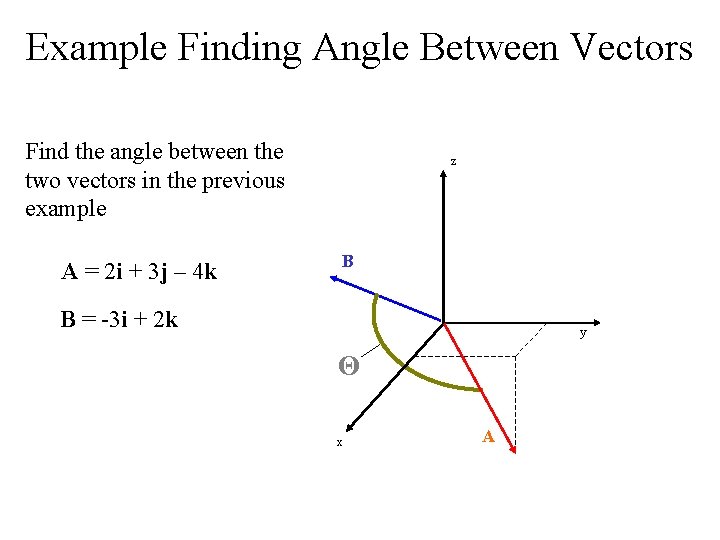
Example Finding Angle Between Vectors Find the angle between the two vectors in the previous example A = 2 i + 3 j – 4 k z B B = -3 i + 2 k y Θ x A

Solution for Finding Angle Use the equation: Θ = cos -1 (A • B) |A| |B| First, we will find (A • B) using the component form: A = 2 i + 3 j – 4 k B = -3 i + 2 k A · B = Ax. Bx + Ay. By + Az. Bz = (2)(-3) + (3)(0) + (-4)(2) = -14 We will then find the magnitude of A and B: |A| = sqrt (22 + 32 + (-4)2) = 5. 385 |B| = sqrt ( (-3)2 + 02 + 22) = 3. 606 -14 136. 13° = Θ = cos -1 (5. 385)(3. 606)

Vector Parallel Components 2. The components of a vector parallel to a given direction. The component of vector A parallel (|A|||) to a direction is defined as: |A||| = |A| cos Θ If the direction is specified by the unit vector u ( since u = 1) we can also determine |A||| from the dot product as: |A||| = |A| cos Θ = A • u Since the dot produces a scalar quantity, this is the magnitude of the vector parallel to the direction. If A|| is positive, the direction is the same as u. If A|| is negative, the direction is opposite that of u.
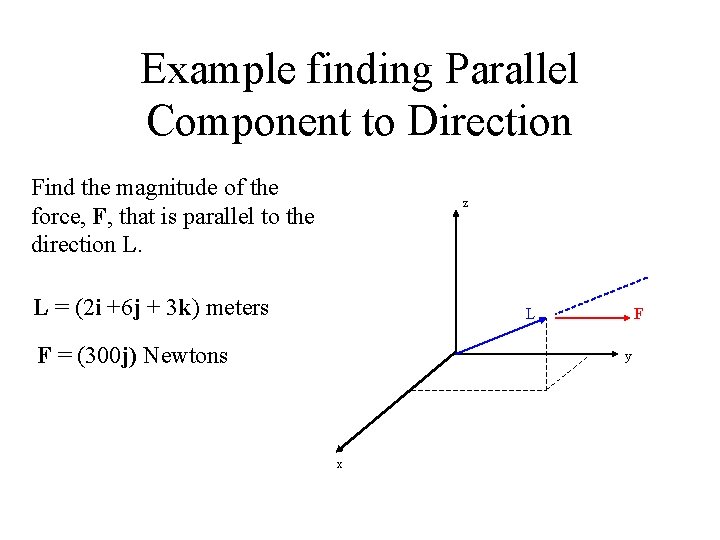
Example finding Parallel Component to Direction Find the magnitude of the force, F, that is parallel to the direction L. z L = (2 i +6 j + 3 k) meters L F = (300 j) Newtons F y x

Solution Finding Parallel Component Use the equation: |A||| = A • u We must first find the unit vector of the given direction L: The unit vector is defined as: u = L / |L| = sqrt (22 + 62 + 32) = 7 u. L = (2 i + 6 j + 3 k) / 7 =. 2865 i +. 857 j +. 429 k |F||| = F • u. L = (300 j Newtons) • (. 2865 i +. 857 j +. 429 k) = (0 i) • (. 286 i) + (300 j) • (. 857 j) + (0 k) • (. 429 k) = 257. 1 Newtons
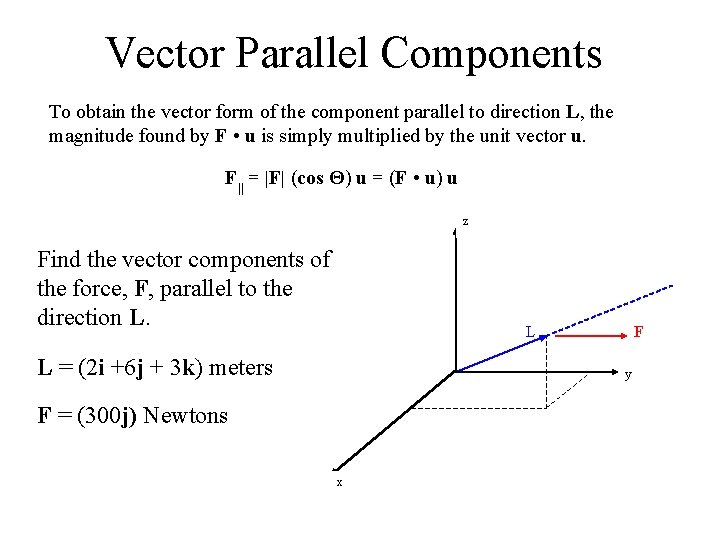
Vector Parallel Components To obtain the vector form of the component parallel to direction L, the magnitude found by F • u is simply multiplied by the unit vector u. F|| = |F| (cos Θ) u = (F • u) u z Find the vector components of the force, F, parallel to the direction L. L L = (2 i +6 j + 3 k) meters F y F = (300 j) Newtons x

Solution Vector Parallel Components In the previous example we found that: |F||| = F • u = 257. 1 Newtons u. L=. 2865 i +. 857 j +. 429 k Then to find the vector components of F parallel to the direction L, use: A|| = (A • u) u F|| = (F • u. L) u. L = ((300 j) • (. 2865 i +. 857 j +. 429 k)) = (257. 1 Newtons) (. 2865 i +. 857 j +. 429 k) = (73. 5 i + 220 j +110 k) N

Finding Vector Perpendicular Components 3. Finding a vector’s components perpendicular to a given direction A vector that is perpendicular, or normal, to a given direction may be found in either scalar or vector form. To find the vector components of the force perpendicular (Fn) to a direction, A|| must first be found. A|| (vector form) is subtracted from the given vector A. An = A - A||
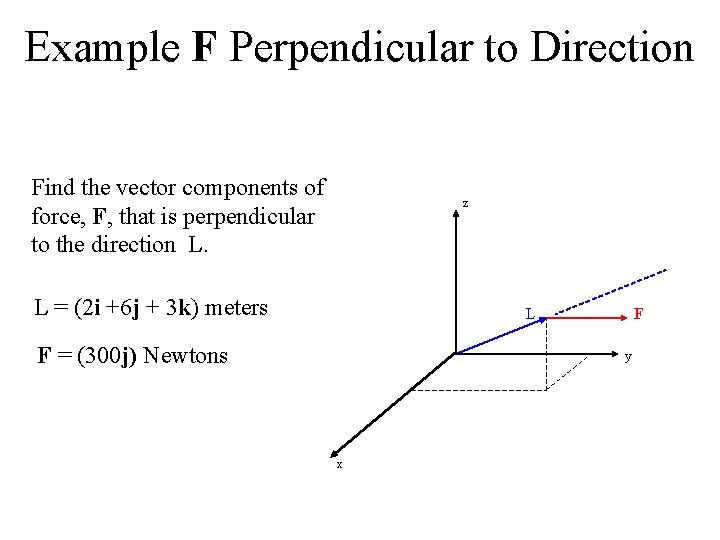
Example F Perpendicular to Direction Find the vector components of force, F, that is perpendicular to the direction L. z L = (2 i +6 j + 3 k) meters L F = (300 j) Newtons F y x

Solution to Finding F Perpendicular From a previous example, we found that: F|| = (73. 5 i + 220 j +110 k) N We know that: F = (300 j) Newtons Use: An = A - A|| Fn = (300 j)N – (73. 5 i + 220 j + 110 k)N Fn = (-73. 5 i + 80 j – 110 k)N

Magnitude of F perpendicular to Direction There are two ways to find the portion of a force perpendicular to a direction If you have already found Fn, the magnitude of the vector form can be taken Given: Fn = Fxi + Fyj + Fzk |F|n= sqrt ( Fx 2 + Fy 2 + Fz 2) The other way is to use the magnitudes of the force and the parallel force: |F|n = sqrt (|F|2 - |F|||2)
Example Magnitude of F Perpendicular to Direction Find the magnitude of the force, F, that is perpendicular to the direction L. z L = (2 i +6 j + 3 k) meters L F = (300 j) Newtons F y x

Solution finding magnitude of F perpendicular Using magnitude of Fn: Fn = (-73. 5 i + 80 j – 110 k)N |F|n= sqrt ( (-73. 5)2 +802 +(-110)2) = 154. 60 Newtons Using |F| and |F||| : |F| = 300 N |F||| = 257. 1 N This error comes from when we rounded 6/7 in the unit vector of L from. 85714 to. 857 |F|n= sqrt (3002 – 257. 12) = 154. 59 Newtons
- Slides: 23