DORUSAL PROGRAMLAMA LP Modelinin Kurulmas rnek 1 n

DOĞRUSAL PROGRAMLAMA

LP Modelinin Kurulması – Örnek 1 n EMA Meyvacılık Almanya’ya elma, muz ve armut ihraç etmektedir. Kasalarda stoklanan bu ürünlerin birim stoklama maliyetleri sırasıyla 7 YTL, 6 YTL ve 9 YTL’dir. Bir kasa elma 5 m 2, bir kasa muz 8 m 2 ve bir kasa armut da 10 m 2 alan kaplamaktadır. Firmanın depolama kapasitesi ise 1000 m 2’dir. Muz çabuk bozulduğu için firma bu meyveden en fazla 150 kasa stoklayabilmektedir. Elma ve armuda olan talep değişkenliğinden dolayı firma bu iki meyvenin her birinden en az 50’şer kasa güven stoku bulundurmak zorundadır. Firmanın toplam stoklama maliyetini minimize eden doğrusal programlama modelini kurunuz. 2

LP Modelinin Kurulması – Örnek 1 Karar değişkenleri: x 1 = elma stoğu x 2 = muz stoğu x 3 = armut stoğu Amaç fonksiyonu: Zenk. = Toplam stoklama maliyeti Zenk. = 7 x 1+6 x 2+9 x 3 Kısıtlar: 1. Kısıt depolama alanı 2. Kısıt muz stoğuna ilişkin kısıt 3. Kısıt elma stoğuna ilişkin kısıt 4. Kısıt armut stoğuna ilişkin kısıt 5 x 1+8 x 2+10 x 3≤ 1000 x 2 ≤ 150 x 1 ≥ 50 x 3 ≥ 50 Pozitiflik kısıtı x 1, x 2, x 3 ≥ 0 3

n n n LP Modelinin – Örnek 2 Bir postane haftanın farklı günlerinde tam. Kurulması gün çalışacak farklı sayıda işçi istihdam etmek istemektedir. Her gün için tam gün çalışması istenilen işçi sayısı aşağıdaki tabloda belirtilmiştir. Çalışma yasalarına göre tam gün çalışan her işçi, haftanın birbirini izleyen beş gününde çalışmak zorundadır, ardından da iki gün dinlenmektedir. Postane günlük gereksinimlerini sadece tam gün çalışan işçiler kullanarak karşılamak istemektedir. İstihdam edilmesi gereken tam gün çalışacak işçi sayısını minimize etmek için gerekli LP modelini kurunuz. Pazartesi 17 Salı 13 Çarşamba 15 Perşembe 19 Cuma 14 Cumartesi 16 Pazar 11 4

LP Modelinin Kurulması – Örnek 2 n n n Karar değişkenleri; xi = i gününde işe başlayan işçi sayısı (i = 1, 2, …, 7) Amaç fonksiyonu; Zenk. = x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + x 7 Kısıtlar; Her gün için çalışması gereken min. işçi sayısı verildiğine göre, x 1 + x 4 + x 5 + x 6 + x 7 ≥ 17 (Pazartesi) x 1 + x 2 + x 5 + x 6 + x 7 ≥ 13(Salı) x 1 + x 2 + x 3 + x 6 + x 7 ≥ 15(Çarşamba) x 1 + x 2 + x 3 + x 4 + x 7 ≥ 19 (Perşembe) x 1 + x 2 + x 3 + x 4 + x 5 ≥ 14 (Cuma) x 2 + x 3 + x 4 + x 5 + x 6 ≥ 16 (Cumartesi) x 3 + x 4 + x 5 + x 6 + x 7 ≥ 11 (Pazar) xi ≥ 0 (i = 1, 2, …, 7) 5

LP Modelinin Kurulması – Örnek 3 n n n n Sailco şirketi gelecek üçer aylık dönemlerde ne kadar üretim yapması gerektiğini saptamak istemektedir. Üçer aylık 4 dönem için talep sırasıyla; 40, 60, 75 ve 25 teknedir. Şirket talebi zamanında karşılamalıdır. Birinci üç aylık dönemin başında şirketin 10 teknelik stoku bulunmaktadır. Her üç aylık dönemin başında o dönemde ne kadar üretim yapılacağına karar verilmesi gerekmektedir. Bir dönemde üretilen teknelerin o dönemin talebini karşılamak için kullanılabileceği varsayılmaktadır. Her üç aylık dönem boyunca şirket normal mesai ile tekne başına toplam $400’a toplam maksimum 40 tekne üretebilmektedir. Fazla mesai ile işçi çalıştırarak tekne başına toplam 450$’a daha fazla tekne üretebilmektedir. Her üç aylık dönemin sonunda (o dönemin üretimi yapılıp talebi karşılandıktan sonra) tekne başına $20 stoklama maliyeti ortaya çıkmaktadır. Gelecek üçer aylık 4 dönem için üretim ve stok maliyetlerini minimize edecek bir üretim programı hazırlanmak istenmektedir. 6

LP Modelinin Kurulması – Örnek 3 n n n Firmanın her üç aylık dönem için normal mesai ve fazla mesai ile ne kadar üretim yapılması gerektiğini belirlemesi gerekmektedir. Bu durumda karar değişkenleri: xt = t. üç aylık dönemde normal mesai ile üretilen teknelerin sayısı ($400/tekne) (t = 1, 2, 3, 4) yt = t. üç aylık dönemde fazla mesai ile üretilen tekne sayısı ($450/tekne) (t = 1, 2, 3, 4) Her üç aylık dönem sonundaki stok (elde kalan tekne sayısı) için belirlenen karar değişkeni: it = t. üç aylık dönem sonunda şirketin elinde kalan tekne sayısı (t = 1, 2, 3, 4) Toplam maliyet = Normal mesai ile tekne üretim maliyeti + fazla mesai ile tekne üretim maliyeti + stok maliyetleri 7

LP Modelinin Kurulması – Örnek 3 n n n Şirketin amaç fonksiyonu: Zenk. = 400 x 1 + 400 x 2 + 400 x 3 + 400 x 4 + 450 y 1 + 450 y 2 + 450 y 3 + 450 y 4 + 20 i 1 + 20 i 2 + 20 i 3 + 20 i 4 t dönemi sonundaki stok = (t -1)dönemi sonundaki stok + t dönemi üretimi – t dönemi talebi dt ile gösterildiğinde (d 1=40, d 2=60, d 3=75, d 4=25) it = it-1 + (xt + yt) – dt (i 0 = 10) it-1 + (xt + yt) ≥ dt olması halinde t dönemi talebi karşılanabilecektir, it + dt ≥ dt yani it ≥ 0 olması kısıtı talebin karşılanmasını kesinleştirecektir. Kısıtlar: Normal mesai ile x 1 ≤ 40, x 2 ≤ 40, x 3 ≤ 40, x 4 ≤ 40 üretim kısıtları i 1 = 10 + x 1 + y 1 – 40 i 2 = i 1 + x 2 + y 2 – 60 Stok kısıtları i 3 = i 2 + x 3 + y 3 – 75 i 4 = i 3 + x 4 + y 4 – 25 it ≥ 0, yt ≥ 0, xt ≥ 0 (t = 1, 2, 3, 4) 8

DOĞRUSAL PROGRAMLAMA SORUNLARINDA GRAFİKSEL ÇÖZÜM YÖNTEMİ 9

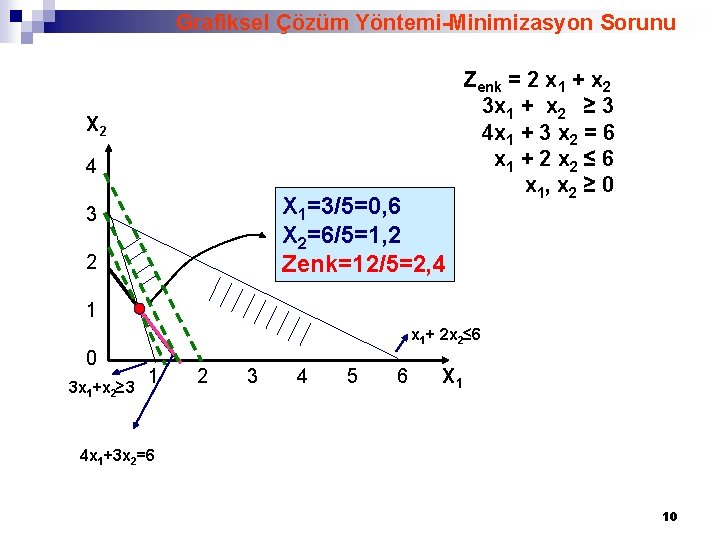
Grafiksel Çözüm Yöntemi-Minimizasyon Sorunu X 2 4 X 1=3/5=0, 6 X 2=6/5=1, 2 Zenk=12/5=2, 4 3 2 Zenk = 2 x 1 + x 2 3 x 1 + x 2 ≥ 3 4 x 1 + 3 x 2 = 6 x 1 + 2 x 2 ≤ 6 x 1, x 2 ≥ 0 1 x 1+ 2 x 2≤ 6 0 3 x 1+x 2≥ 3 1 2 3 4 5 6 X 1 4 x 1+3 x 2=6 10

SİMPLEKS YÖNTEMİ 11

Simpleks Yöntemi – Örnek n Bir işletme x 1 ve x 2 gibi iki ürün üretmektedir. Mamul Üretim faktörü X 1 X 2 Kapasite A 7 6 84 B 4 2 32 Kar 11 4 §Zenb. = 11 x 1 + 4 x 2 + 0 s 1 + 0 s 2 7 x 1 + 6 x 2 + s 1 = 84 4 x 1 + 2 x 2 + s 2 = 32 x 1, x 2, s 1, s 2 ≥ 0 84/7 = 12 32/4 = 8 Zenb. = 11 x 1 + 4 x 2 7 x 1 + 6 x 2 ≤ 84 4 x 1 + 2 x 2 ≤ 32 x 1, x 2 ≥ 0 Başlangıç Simpleks Tablo Cj 11 Değişken karışımı nicelik X 1 4 0 0 X 2 s 1 s 2 0 s 1 84 7 6 1 0 0 s 2 32 4 2 0 1 0 0 0 11 4 0 0 Zj Cj - Z j 12

n n Simpleks – Örnek Çözümden çıkacak değişkenin sırasındaki bütün Yöntemi değerler kesişme değerine bölünerek, yeni tabloda bir önceki çözümdeki sıranın yerine geçecek sıra belirlenir. Diğer sıralardaki değerlerin hesaplanması için aşağıdaki formül kullanılır: (eski sıradaki değer) – [(eski sıradaki kesişme değeri) x (yerine geçen sıradaki o kolona isabet eden değer)] Birinci Simpleks Tablo (Optimal) Cj 11 4 0 0 Değişken karışımı nicelik X 1 X 2 s 1 s 2 0 s 1 28 0 5/2 1 -7/4 11 x 1 8 1 1/2 0 ¼ 88 11 11/2 0 11/4 0 -3/2 0 -11/4 Zj Cj - Z j X 1 = 8 s 1 = 28 Z = 88 13

BÜYÜK M YÖNTEMİ 14

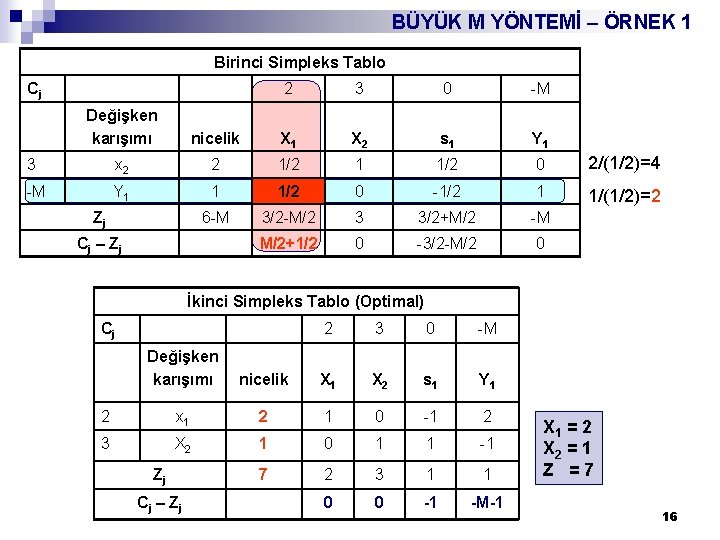
Zenb. = 2 x 1 + 3 x 2 x 1 + 2 x 2 ≤ 4 x 1 + x 2 = 3 x 1, x 2 ≥ 0 Z = 2 x 1 + 3 x 2 + 0 s 1 – MY 1 – ÖRNEK 1 x 1 + 2 x 2 BÜYÜK + s 1 M=YÖNTEMİ 4 x 1 + x 2 + 1 Y 1 = 3 x 1, x 2, s 1, Y 1 ≥ 0 Başlangıç Simpleks Tablo Cj 2 3 0 -M Değişken karışımı nicelik X 1 X 2 s 1 Y 1 0 s 1 4 1 2 1 0 4/2=2 -M Y 1 3 1 1 0 1 3/1=3 -3 M -M -M 0 -M 2+M 3+M 0 0 Zj Cj – Z j 15

BÜYÜK M YÖNTEMİ – ÖRNEK 1 Birinci Simpleks Tablo Cj 2 3 0 -M Değişken karışımı nicelik X 1 X 2 s 1 Y 1 3 x 2 2 1/2 1 1/2 0 2/(1/2)=4 -M Y 1 1 1/2 0 -1/2 1 1/(1/2)=2 6 -M 3/2 -M/2 3 3/2+M/2 -M M/2+1/2 0 -3/2 -M/2 0 Zj Cj – Z j İkinci Simpleks Tablo (Optimal) Cj 2 3 0 -M Değişken karışımı nicelik X 1 X 2 s 1 Y 1 2 x 1 2 1 0 -1 2 3 X 2 1 0 1 1 -1 7 2 3 1 1 0 0 -1 -M-1 Zj Cj – Z j X 1 = 2 X 2 = 1 Z =7 16

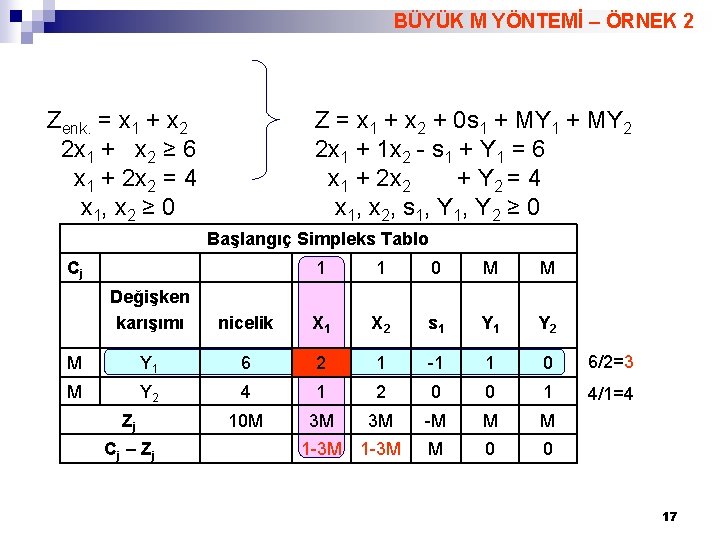
BÜYÜK M YÖNTEMİ – ÖRNEK 2 Zenk. = x 1 + x 2 2 x 1 + x 2 ≥ 6 x 1 + 2 x 2 = 4 x 1, x 2 ≥ 0 Z = x 1 + x 2 + 0 s 1 + MY 2 2 x 1 + 1 x 2 - s 1 + Y 1 = 6 x 1 + 2 x 2 + Y 2 = 4 x 1, x 2, s 1, Y 2 ≥ 0 Başlangıç Simpleks Tablo Cj 1 1 0 M M Değişken karışımı nicelik X 1 X 2 s 1 Y 2 M Y 1 6 2 1 -1 1 0 6/2=3 M Y 2 4 1 2 0 0 1 4/1=4 10 M 3 M 3 M -M M M 1 -3 M M 0 0 Zj Cj – Z j 17

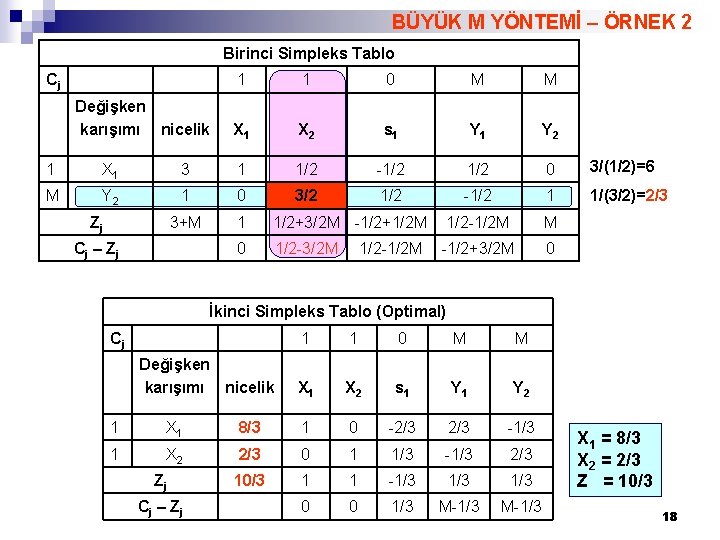
BÜYÜK M YÖNTEMİ – ÖRNEK 2 Birinci Simpleks Tablo Cj Değişken karışımı nicelik 1 1 0 M M X 1 X 2 s 1 Y 2 1 X 1 3 1 1/2 -1/2 0 3/(1/2)=6 M Y 2 1 0 3/2 1/2 -1/2 1 1/(3/2)=2/3 3+M 1 1/2+3/2 M -1/2+1/2 M 1/2 -1/2 M M 0 1/2 -3/2 M -1/2+3/2 M 0 Zj Cj – Z j 1/2 -1/2 M İkinci Simpleks Tablo (Optimal) Cj Değişken karışımı nicelik 1 1 0 M M X 1 X 2 s 1 Y 2 1 X 1 8/3 1 0 -2/3 -1/3 1 X 2 2/3 0 1 1/3 -1/3 2/3 10/3 1 1 -1/3 1/3 0 0 1/3 M-1/3 Zj Cj – Z j X 1 = 8/3 X 2 = 2/3 Z = 10/3 18