Doppler Shift and Stellar Magnitudes Energy Power Units

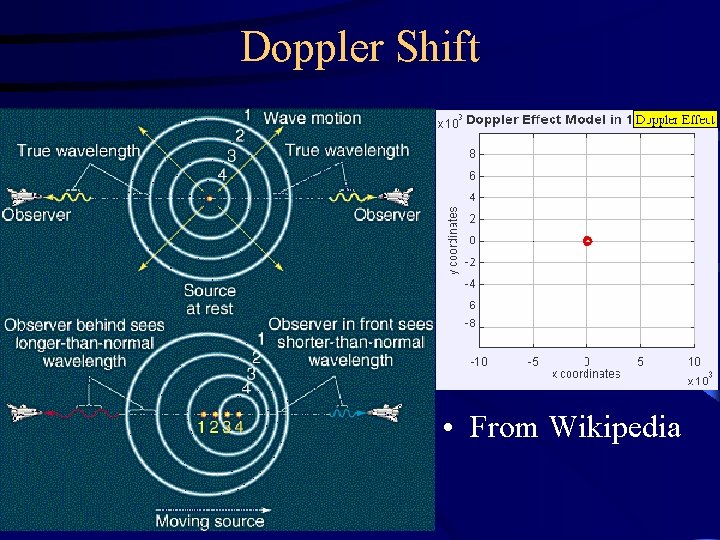
Doppler Shift and Stellar Magnitudes

Energy & Power Units • Energy has units Joule (J) • Rate of energy expended per unit time is called power, and has units Watt (W) • Example: a 100 W = 100 J/s light bulb emits 100 J of energy every second • Nutritional Value: energy your body gets out of food, measured in Calories = 1000 cal = 4200 J • Luminosity is the same as power radiated

Stefan’s Law • A point on the Blackbody curve tells us how much energy is radiated per frequency interval • Question: How much energy is radiated in total, i. e. how much energy does the body lose per unit time interval? • Stefan(-Boltzmann)’s law: total energy radiated by a body at temperature T per second: P = A σ T 4 • σ = 5. 67 x 10 -8 W/(m 2 K 4)

Example: Stefan-Boltzmann Law • Sun T=6000 K, Earth t=300 K (or you!) • How much more energy does the Sun radiate per time per unit area? • Stefan: Power radiated is proportional to the temperature (in Kelvin!) to the fourth power • Scales like the fourth power! • Factor f=T/t=20, so f 4 =204=24 x 104=16 x 104 • 160, 000 x

Example: Wien’s Law • Sun T=6000 K, Earth t=300 K (or you!) • The Sun is brightest in the visible wave lengths (500 nm). At which wave lengths is the Earth (or you) brightest? • Wien: peak wave length is proportional to temperature itself Scales linearly! • Factor f=T/t=20, so f 1 =201=20, so peak wavelength is 20 x 500 nm=10, 000 nm = 10 um • Infrared radiation!

Doppler Shift • From Wikipedia

Doppler Shift • Can use the Doppler shift to determine radial velocity of distant objects relative to us • Transverse velocity can be measured from the motion of stars with respect to background over a period of years – (Halley 1718: Sirius, Arcturus, Aldebaran moved since Hipparchus, 1850 years ago)

The Magnitude Scale • A measure of the apparent brightness • Logarithmic scale • Notation: 1 m. 4 (smaller brighter) • Originally six groupings – 1 st magnitude the brightest – 6 th magnitude is 100 x dimmer • So a difference of 5 mag is a difference of brightness of 100 • Factor 2. 512=1001/5 for each mag.

Absolute Magnitude • The absolute magnitude is the apparent magnitude a star would have at a distance of 10 pc. • Notation example: 2 M. 8 • It is a measure of a star’s actual or intrinsic brightness called luminosity • Example: Sirius: 1 M. 4, Sun 4 M. 8 – Sirius is intrinsically brighter than the Sun

Finding the absolute Magnitude • To figure out absolute magnitude, we need to know the distance to the star • Then do the following Gedankenexperiment: – In your mind, put the star from its actual position to a position 10 pc away – If a star is actually closer than 10 pc, its absolute magnitude will be a bigger number, i. e. it is intrinsically dimmer than it appears – If a star is farther than 10 pc, its absolute magnitude will be a smaller number, i. e. it is intrinsically brighter than it appears