Doppler Effect The Doppler effect is the shift

Doppler Effect ØThe Doppler effect is the shift in frequency and wavelength of waves that results from a moving source and/or moving observer relative to the wave medium ØConsider a point source of traveling waves (a siren) at some frequency f 0 n We have λ=V/f 0 where V is the wave velocity and V depends on the characteristics of the medium alone 1

Doppler Effect Ø A source moving towards an observer with velocity vs n The observer sees wave fronts that are “squeezed” in the direction of vs but the wave velocity remains unchanged Ø A source moving away from an observer 2

Doppler Effect 3

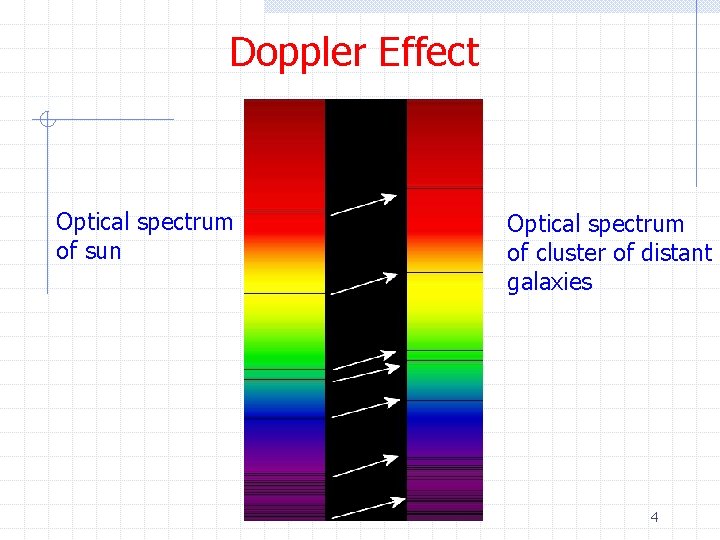
Doppler Effect Optical spectrum of sun Optical spectrum of cluster of distant galaxies 4

Doppler Effect Ø An observer moving towards a source with velocity vo n Here an observer will see the same wavelength λ but with a higher wave velocity (e. g. wading into an ocean) Ø An observer moving away from a source 5

Doppler Effect Ø In the case of light waves n Classical, moving source n Classical, moving observer Ø Makes sense, the frequency is higher if observer and source approach each other and lower if they are receding 6

Doppler Effect ØBut n n This is a classical calculation There is an asymmetry between moving source and moving observer w Moving source w Moving observer 7

Doppler Effect ØThe relativistic Doppler effect calculation differs from the classical one because of time dilation ØConsider a source of frequency f 0 fixed in S’ n n n As usual, S’ is moving with velocity V relative to S N = f 0Δt’ waves are emitted in Δt’ Δt=γΔt’ 8

Doppler Effect Ø In S, with the source in S’ moving towards the observer in S n During Δt, the first wave moves cΔt and the source moves VΔt The wavelength in S is n Now n 9

Doppler Effect Doppler effect Ø Still in S, we find the relativistic for the source approaching Ø For the source receding, we have 10

Doppler Effect Ø For completeness, consider the source of frequency f 0 be fixed in S and let Δt=λ/c Ø In S’, let the observer see the source receding 11

Doppler Effect Ø In S’, if the observer sees the source approaching we would find 12

Doppler Effect Ø In summary n For source and/or observer approaching n For source and/or observer receding Ø In special relativity, the two situations (source moving or observer moving) give the same result Ø There is also a transverse Doppler effect that does not occur classically 13

Doppler Effect ØAn astronaut tries to get out of a traffic violation for running a red light (λ=670 nm) by arguing the Doppler effect made the light appear green (λ=540 nm). ØWhat was the velocity of the astronaut? 14

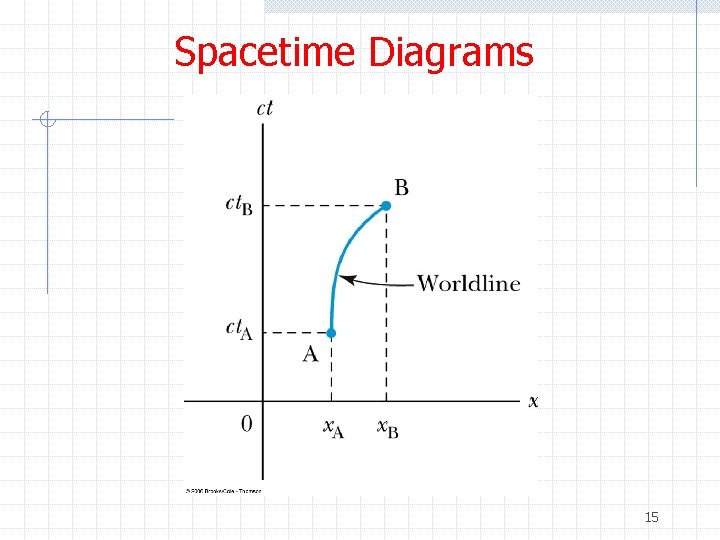
Spacetime Diagrams 15

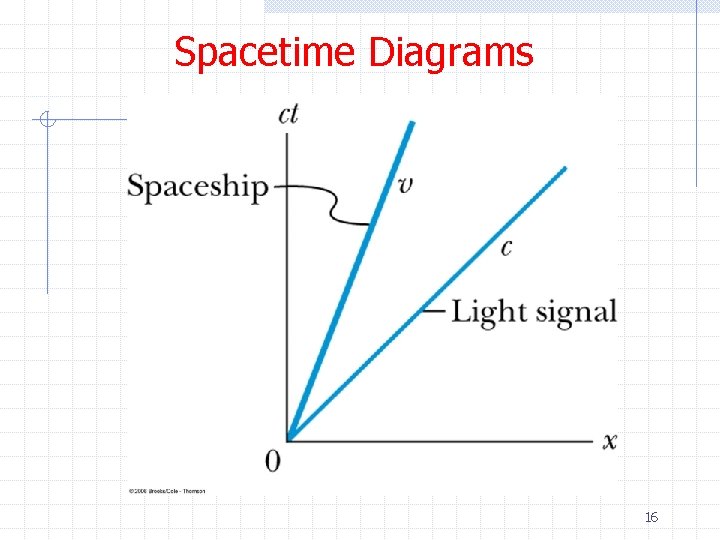
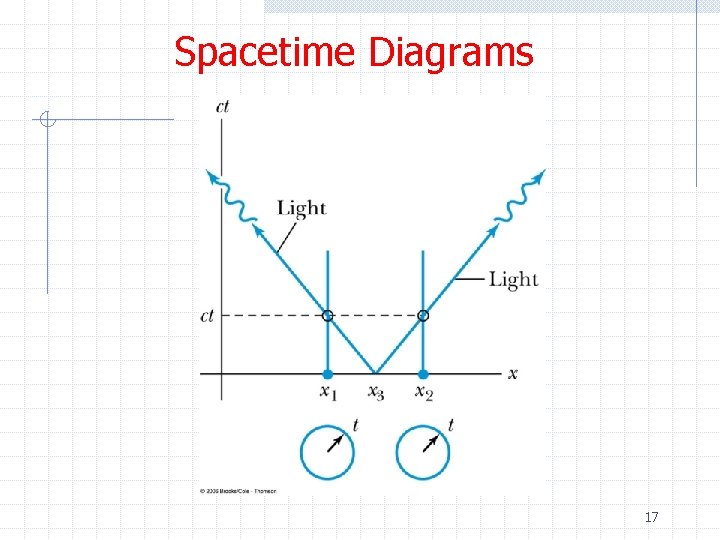
Spacetime Diagrams 16

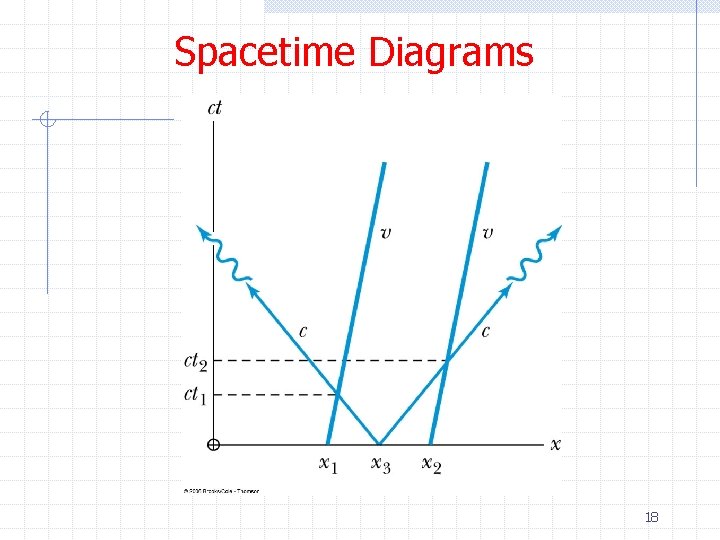
Spacetime Diagrams 17

Spacetime Diagrams 18

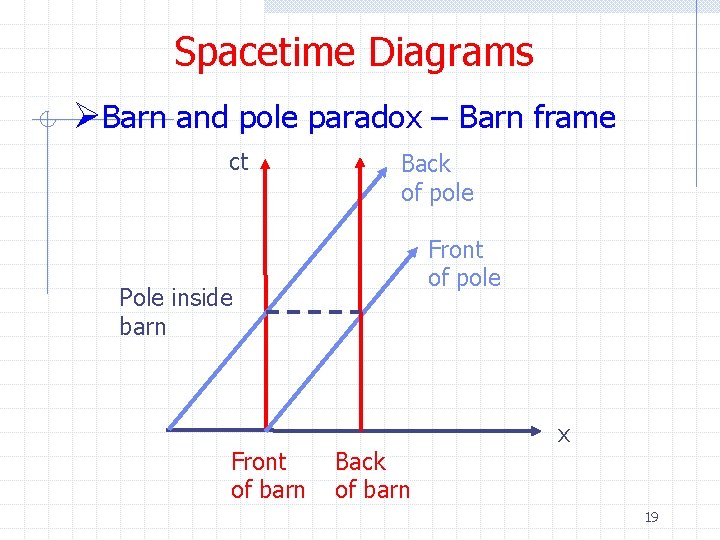
Spacetime Diagrams ØBarn and pole paradox – Barn frame ct Back of pole Front of pole Pole inside barn Front of barn Back of barn x 19

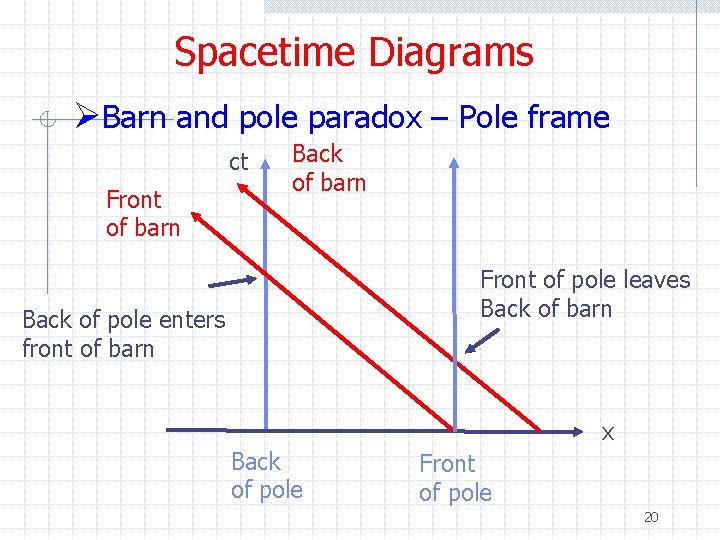
Spacetime Diagrams ØBarn and pole paradox – Pole frame ct Front of barn Back of barn Front of pole leaves Back of barn Back of pole enters front of barn x Back of pole Front of pole 20

Spacetime Diagrams ct ct’ x’ x 21

Spacetime Diagrams 22