Dont Care Minimization of BMDs Complexity and Algorithms

Don´t Care Minimization of *BMDs: Complexity and Algorithms Christoph Scholl Marc Herbstritt Bernd Becker Institute of Computer Science Albert-Ludwigs-University 79110 Freiburg im Breisgau, Germany 1

Overview • • Motivation Decision Diagrams: BDDs, BMDs and *BMDs More details on BMDs Problem Formulation Complexity Results Algorithms Experiments Conclusions 2

Motivation • Decision Diagrams (DDs): – function representation – used in: logic synthesis, testing, and verification • Don´t Care conditions: – can occur between function modules – by system specification è Use Don´t Cares to minimize DD-representation – well-known for bit-level DDs (BDD, FDDs) – unknown for word-level DDs (BMD, *BMDs, . . . ) 3

Related Work • Zilic, Radecka, IWLS, 1998: „Don´t Care FDD minimization by interpolation“ Problem: FDD represents boolean function, *BMD represents integer-valued function • Varma, Trachtenberg, IEE Proceedings, 1991: „Computation of Reed-Muller expansions of incompletely specified boolean functions from reduced representations“ Problem: Spectral technique not applicable in case of integer-valued functions 4

Decision Diagrams: BDDs • Representation for boolean functions: • Iterative Shannon-decomposition: • Transformation into directed, acylic graph: v low(v) high(v) • Reduction: eliminate v iif low(v)=high(v) 5

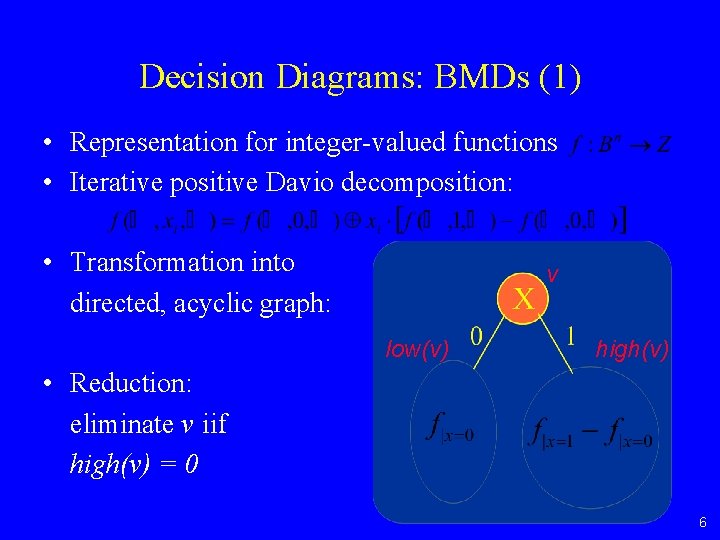
Decision Diagrams: BMDs (1) • Representation for integer-valued functions • Iterative positive Davio decomposition: • Transformation into directed, acyclic graph: v low(v) high(v) • Reduction: eliminate v iif high(v) = 0 6

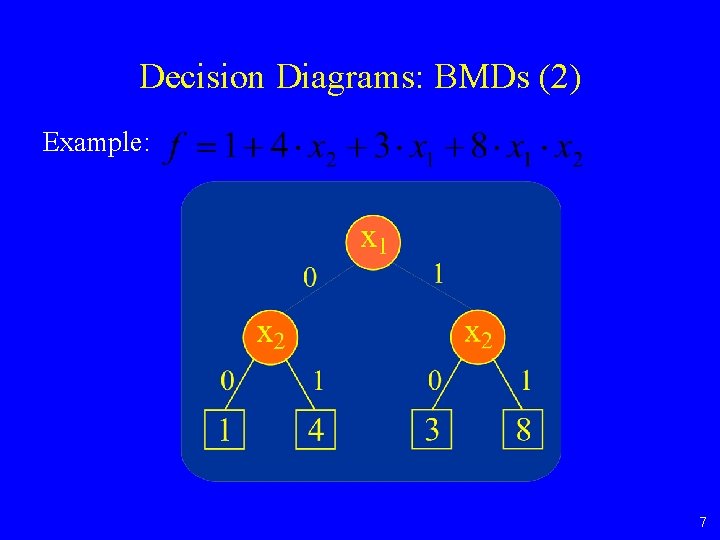
Decision Diagrams: BMDs (2) Example: 7

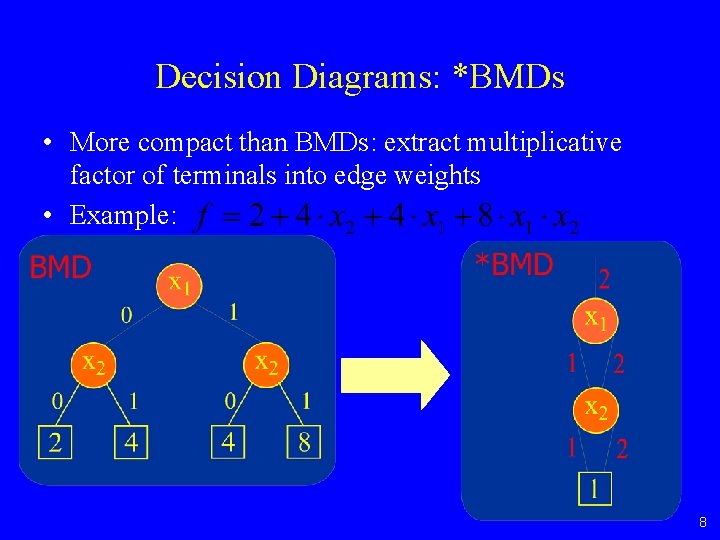
Decision Diagrams: *BMDs • More compact than BMDs: extract multiplicative factor of terminals into edge weights • Example: 8

BMD-nodes reached by • Node v labeled with variable • low(v)=0 -successor(v), high(v)=1 -successor(v) • Node reached by – Follow – Special case: Let : starting at root node not labeled with , choose with: • Go to node 9

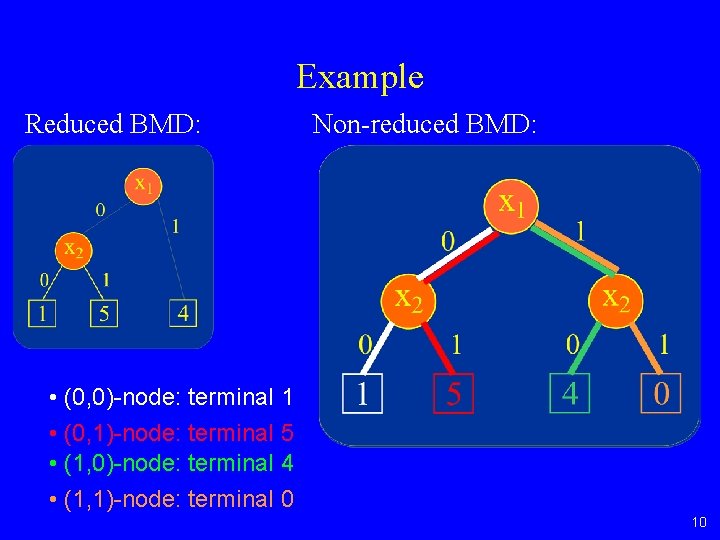
Example Reduced BMD: Non-reduced BMD: • (0, 0)-node: terminal 1 • (0, 1)-node: terminal 5 • (1, 0)-node: terminal 4 • (1, 1)-node: terminal 0 10

Function represented by a BMD-node • Let B be a BMD, • Funtion represented by v is: , v is a -node. Modification of -node, , changes function represented by node v 11

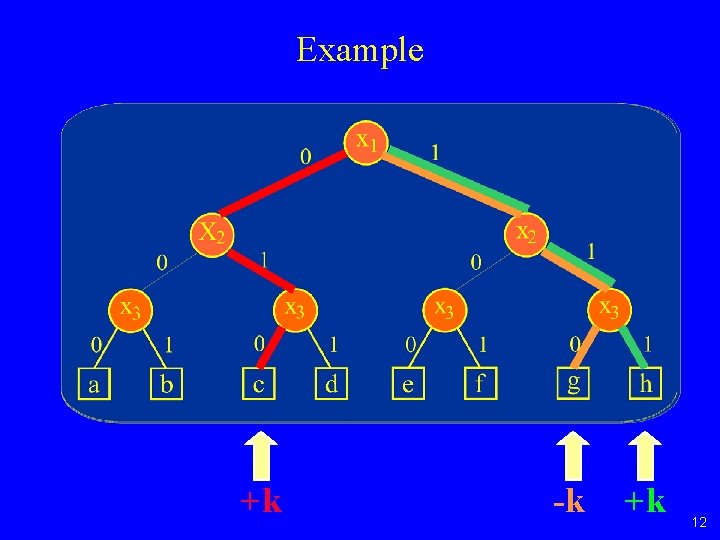
Example +k -k +k 12

Problem Formulation Problem: DC*BMD Given: *BMD B, BDD C, Find: *BMD B*, such that and B* has minimal number of nodes. Problem: DCBMD Like DC*BMD , but BMD instead of *BMD. 13

Complexity Theorem: DC*BMD and DCBMD are NP-complete. Proof: NP-hardness: Reduction from graph colorability problem. NP-membership: Using WLCDs. 14

Method min_polynomial (1) • Idea: Minimize size of polynomial extracted from BMD • Polynomial contains term with is terminal iif node reached by • Size of BMD B, , is less or equal to size of polynomial representing. • Property holds also for *BMDs. 15

Method min_polynomial (2) • Try to change terminal c reached by have value 0 by using don´t cares. • If , change to : to • Important: Adjustment of all terminals 16

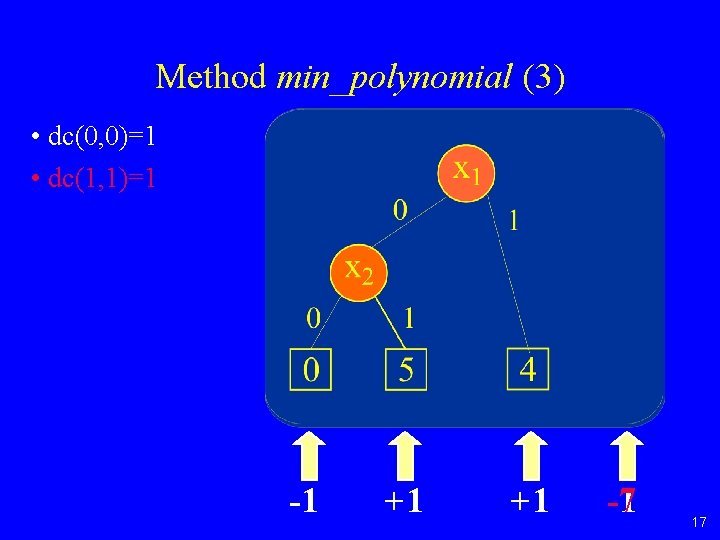
Method min_polynomial (3) • dc(0, 0)=1 • dc(1, 1)=1 -1 +1 +1 -1 -7 17

Method min_polynomial (4) *BMD min_polynomial( *BMD b, BDD dc) 1. if dc=1 return 0; if dc=0 return b; if b=constant return b 2. if (result, b, dc) in Computed Table return result 3. Let v be top variable of b and dc 4. b*low=min_polynomial(blow, dclow) 5. b*high=min_polynomial(bhigh +(blow- b*low), dchigh) 6. b*= b*low+v* b*high 7. if size(b*) size(b) then b*= b 8. insert (b*, b, dc) into Computed Table 9. return b* 18

Method independent_dfs (1) • Idea: Use don´t cares to assign high(v) to 0 application of Davio-reduction rule. • At node v, to check if w=high(v) can be set to 0: 1. check if low(w) can be set to 0, 2. if 1. succeeds, check if high(w) can be set to 0. 19

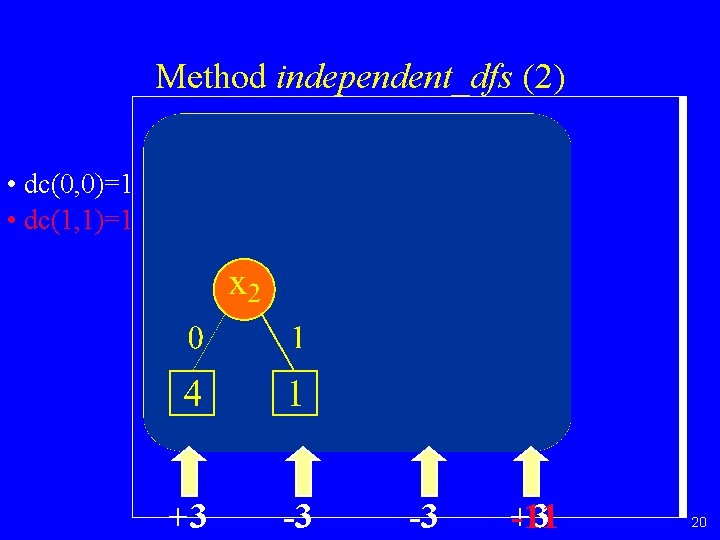
Method independent_dfs (2) • dc(0, 0)=1 • dc(1, 1)=1 +3 -3 -3 -11 +3 20

Method independent_dfs (3) *BMD independent_dfs( *BMD b, BDD dc) 1. if dc=1 return 0; if dc=0 return b; if b=constant return b 2. if (result, b, dc) in Computed Table return result 3. Let v be top variable of b and dc# 4. (success, blow-diff)=check_zero(bhigh , dclow , dchigh) 5. if success then b*=independent_dfs(blow+blow-diff , dclow*dchigh) else b* low =independent_dfs(blow, dclow) b* high =independent_dfs(bhigh +(blow -b* low ), dchigh) b*= b* low +v* b* high 7. if size(b*) size(b) then b*= b 8. insert (b*, b, dc) into Computed Table 9. return b* 21

Experimental Results (1) • Experimental setup: – Generated incompletely specified functions: • Collapse benchmark to sum-of-products • Select cubes with probability of 40% to be included in Don´t Care set • Compute BDD C for Don´t Care Set – Build *BMD B for the outputs of the benchmark, where is: – Compute min_polynomial(B, C) and independent_dfs(B, C) 22

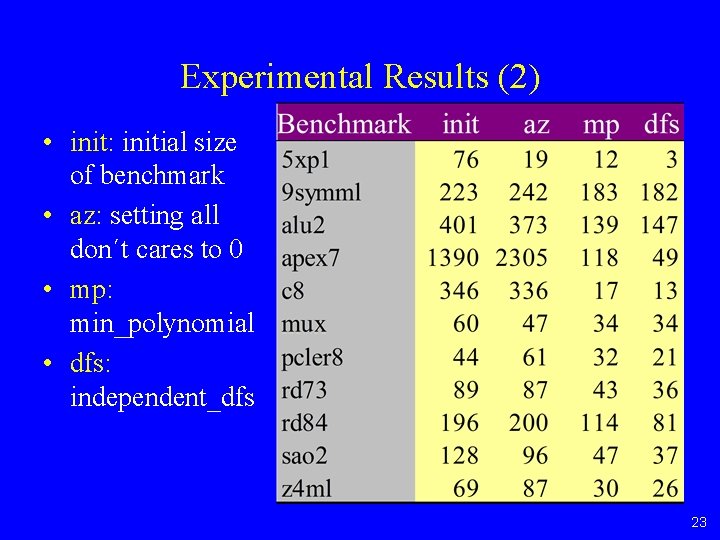
Experimental Results (2) • init: initial size of benchmark • az: setting all don´t cares to 0 • mp: min_polynomial • dfs: independent_dfs 23

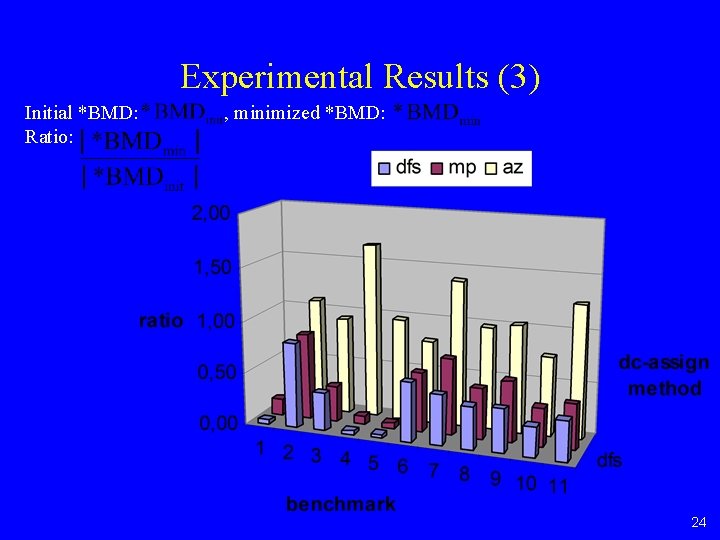
Experimental Results (3) Initial *BMD: Ratio: , minimized *BMD: 24

Conclusions • We presented methods do minimize *BMD/BMDs using Don´t Care conditions • Two methods: min_polynomial, independent_dfs – very effective in reducing the size of *BMDs – time efficient (most benchmarks finish in a few seconds) 25

Future Work • Modification of independent_dfs to independent_bfs: Idea: Don´t care assignments which could be made „at the top in the right half“ of the *BMD can become not applicable due to assignments made „at the bottom in the left half“ • Extension of existing methods to K*BMDs: K*BMDs use several decomposition types: Shannon, positive and negative Davio • Application of Don´t Care based minimization methods for verification of division circuits 26