DoNow Complete the truth table below p q

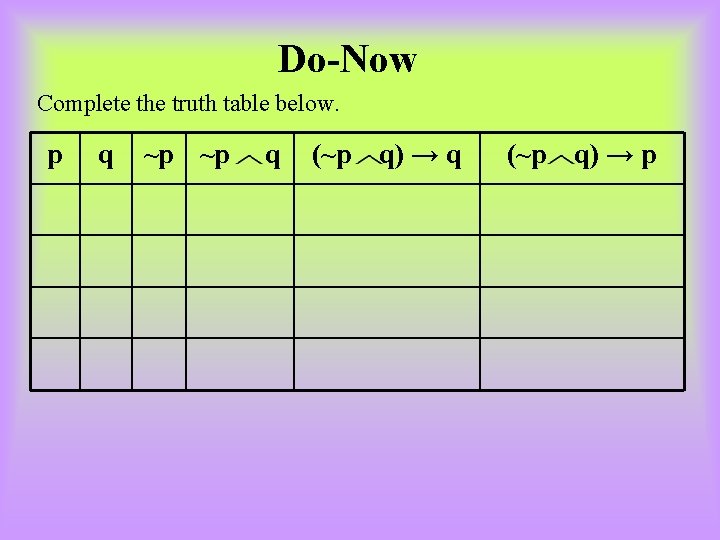
Do-Now Complete the truth table below. p q ~p ~p q (~p q) → p

Laws of Inference Remember and = p or = p q q if…then = p → q De. Morgan’s Law ~(p q) = ~p ~q Negate each of the following compound statements. s ~t ~x y

Law of Disjunctive Inference If p q is true and ~q is true, then p is automatically true. p q ~q p Example: We’ll go to school or we’ll go shopping. We won’t go shopping. x y ~x p m ~m ~b b ~s

Simplify ~(m ~y) ~(k p) Draw a conclusion for each. m→c m ~e e f ~r n ~n

Law of Detachment If p → q is true and p is true, then q is automatically true. x → y ~x Example: If I play baseball, then I need a bat. true What else is true? r → s r ~m → y ~m

Contrapositive Inference Double Negation Chain Rule (~p) p → q q → r p → q ~q

2 -Column Proofs Need to prove whatever they tell you to using the Laws of Inference. Given: (r p → qs) → t q→r ~t rp r ~s Statements Reasons

Statements Reasons F – “We save fuel. ” E – “There’s an energy crisis. ” L – “Workers lose their jobs. ” S – “Schools will close. ” If we save fuel, then there’s not an energy crisis. There’s an energy crisis or workers do not lose their jobs. We save fuel. Workers do not lose their jobs.