Donald E Knuth 1938 The father of algorithm

Donald E. Knuth (1938 ---) The father of algorithm analysis popularizing asymptotic notation. The author of TAOCP -- The Art of Computer Programming • Volume 1: Fundamental Algorithms • Volume 2: Seminumerical Algorithms • Volume 3: Sorting and Searching (among tons of others) “ I have been a happy man ever since January 1, 1990, when I no longer had an email address. ” 10/28/2021 IT 279 1

TAOCP – The Art of Computer Programming • Volume 1: Fundamental Algorithms Basic Concepts and Information Structures • Volume 2: Seminumerical Algorithms Random numbers and Arithmetic • Volume 3: Sorting and Searching Donald E. Knuth • Volume 4: Combinatorial Algorithms Combinatorial Searching and Recursion • Volume 5: Syntactical Algorithms Lexical Scanning and Parsing Techniques • Volume 6: Theory of Languages Mathematical Linguistics • Volume 7: Compiler Highlighted in the preface of Vol. 1 10/28/2021 Programming Language Translation IT 279 2

“An algorithm must be seen to be believed” -- Donald E. Knuth -- Sorting algorithms 10/28/2021 IT 279 3

Sorting: Arranging items into a certain order. Items can be stored in an one dimensional array or linked list, or trees. We prefer using one dimensional array Why? 10/28/2021 IT 279 4

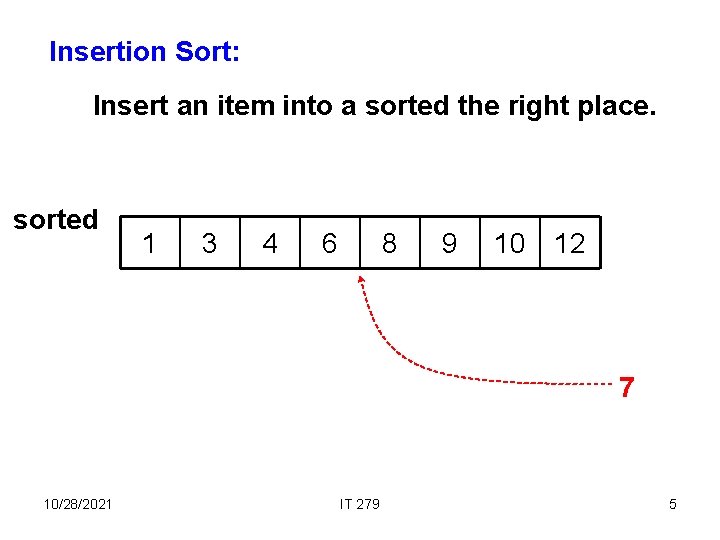
Insertion Sort: Insert an item into a sorted the right place. sorted 1 3 4 6 8 9 10 12 7 10/28/2021 IT 279 5

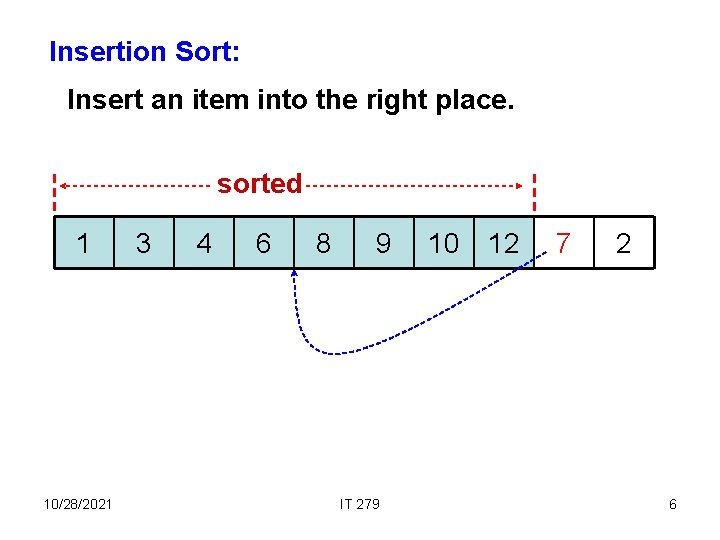
Insertion Sort: Insert an item into the right place. sorted 1 10/28/2021 3 4 6 8 9 IT 279 10 12 7 2 6

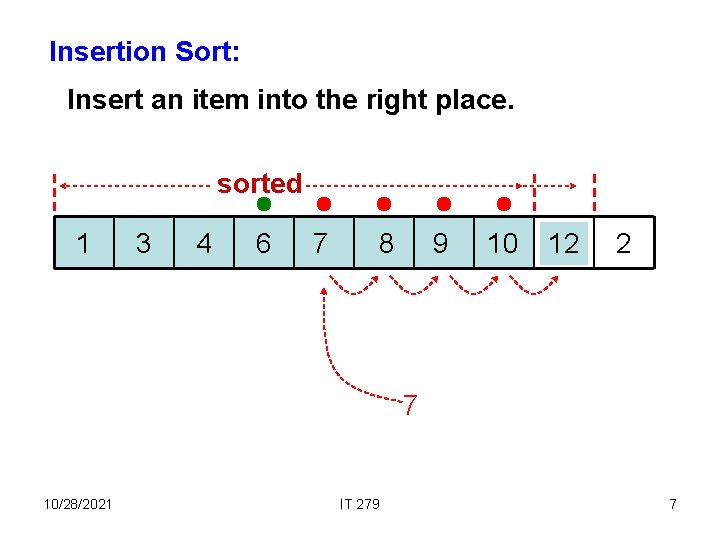
Insertion Sort: Insert an item into the right place. sorted 1 3 4 6 78 98 10 12 9 10 7 12 2 7 10/28/2021 IT 279 7

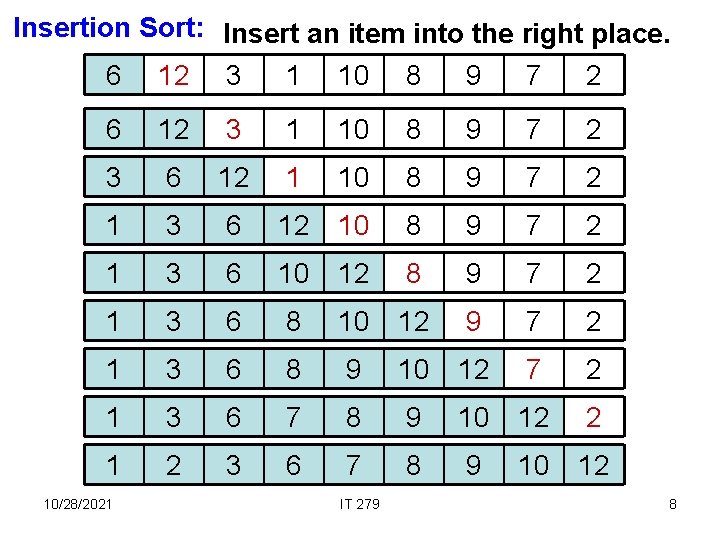
Insertion Sort: Insert an item into the right place. 6 12 3 1 10 8 9 7 2 3 6 12 1 10 8 9 7 2 1 3 6 12 10 8 9 7 2 1 3 6 10 12 8 9 7 2 1 3 6 8 10 12 9 7 2 1 3 6 8 9 10 12 7 2 1 3 6 7 8 9 10 12 2 1 2 3 6 7 8 9 10 12 10/28/2021 IT 279 8

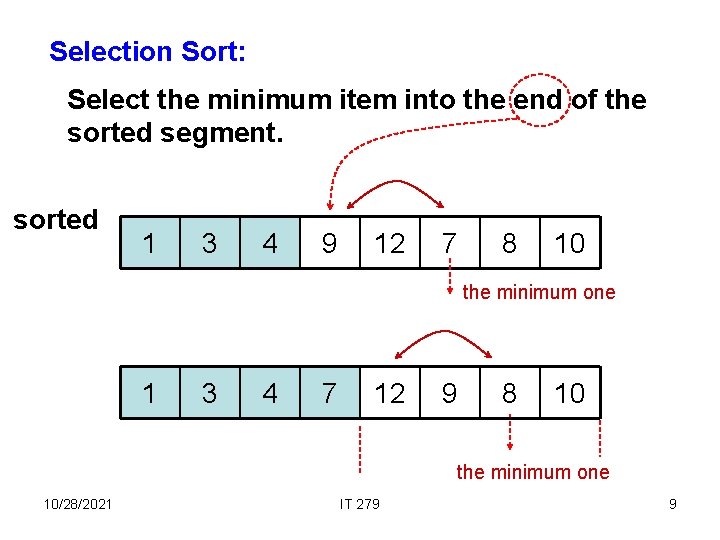
Selection Sort: Select the minimum item into the end of the sorted segment. sorted 1 3 4 9 12 7 8 10 the minimum one 1 3 4 7 12 9 8 10 the minimum one 10/28/2021 IT 279 9

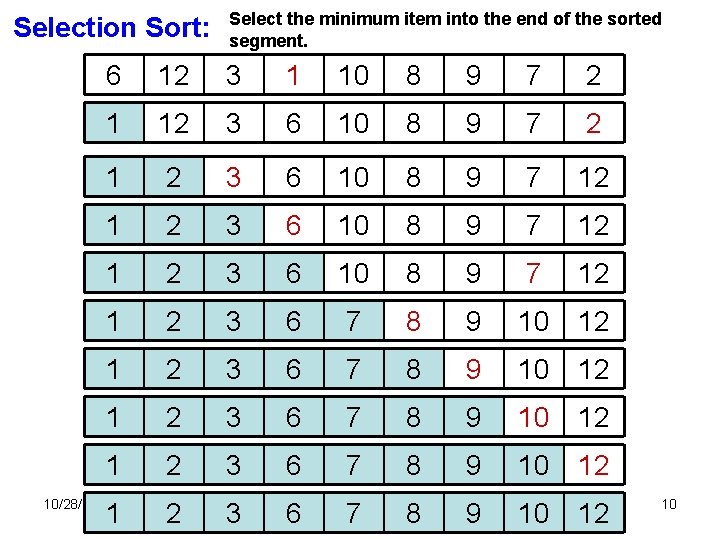
Selection Sort: Select the minimum item into the end of the sorted segment. 6 12 3 1 10 8 9 7 2 1 12 3 6 10 8 9 7 2 1 2 3 6 10 8 9 7 12 1 2 3 6 7 8 9 10 12 2 3 6 8 9 10 12 10/28/2021 1 IT 279 7 10

Analysis of Insertion/Selection Sorts: T(n) = 1 +2 + 3 +. . . + n = O(n 2) O(n 3/2) Shell Sort D. L. Shell, (1959) O(n log n) Lower bound of sorting algorithms 10/28/2021 IT 279 11

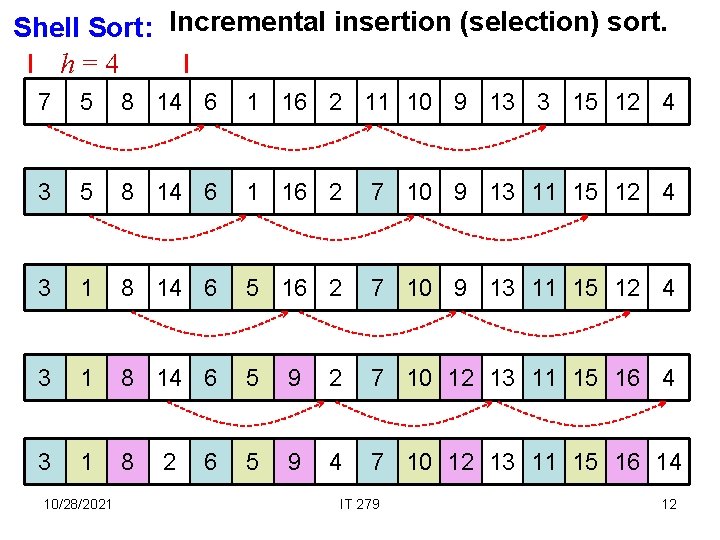
Shell Sort: Incremental insertion (selection) sort. h=4 7 5 8 14 6 1 16 2 11 10 9 13 3 15 12 4 3 5 8 14 6 1 16 2 7 10 9 13 11 15 12 4 3 1 8 14 6 5 9 2 7 10 12 13 11 15 16 4 3 1 8 5 9 4 7 10 12 13 11 15 16 14 10/28/2021 2 6 IT 279 12

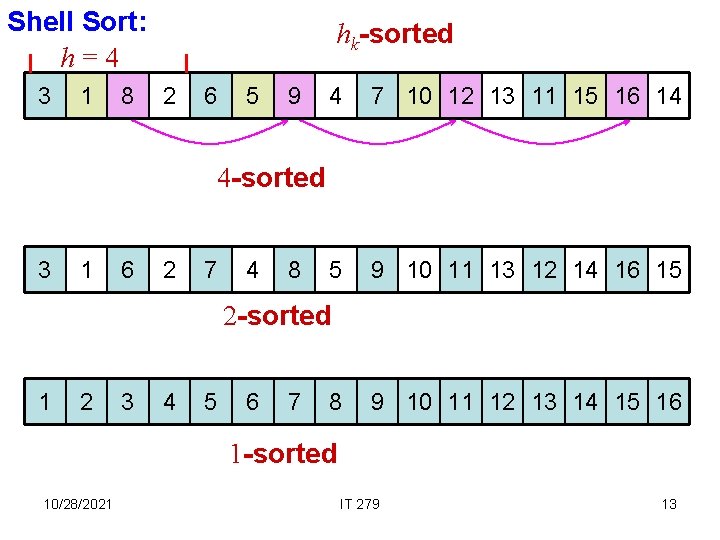
Shell Sort: h=4 3 1 8 hk-sorted 2 6 5 9 4 7 10 12 13 11 15 16 14 5 9 10 11 13 12 14 16 15 4 -sorted 3 1 6 2 7 4 8 2 -sorted 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 -sorted 10/28/2021 IT 279 13

Shell Sort: Incremental insertion with Increment sequence, hk-sorted ht-1 -sorted hk-1 -sorted (implies) hk-sorted hk-1 -sorted 10 9 30 20 hk-sorted Shell suggested: Not a good suggestion, worst case: O(n 2) 10/28/2021 IT 279 14

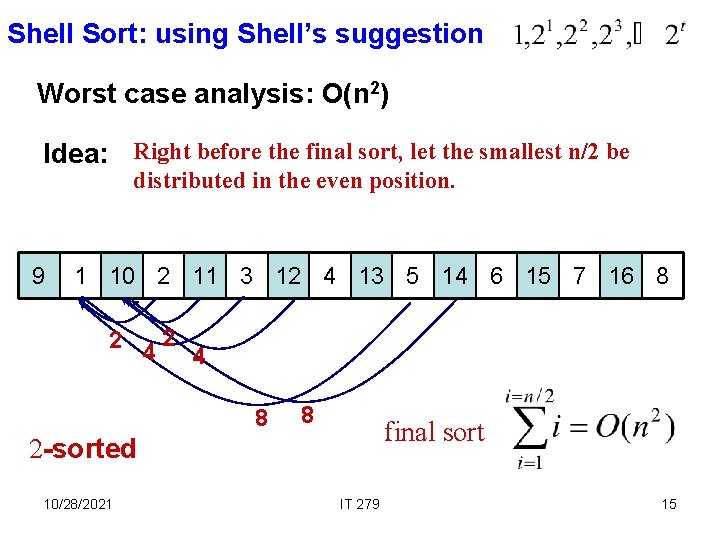
Shell Sort: using Shell’s suggestion Worst case analysis: O(n 2) Idea: Right before the final sort, let the smallest n/2 be distributed in the even position. 9 1 10 2 11 3 12 4 13 5 14 6 15 7 16 8 2 42 4 8 8 final sort 2 -sorted 10/28/2021 IT 279 15

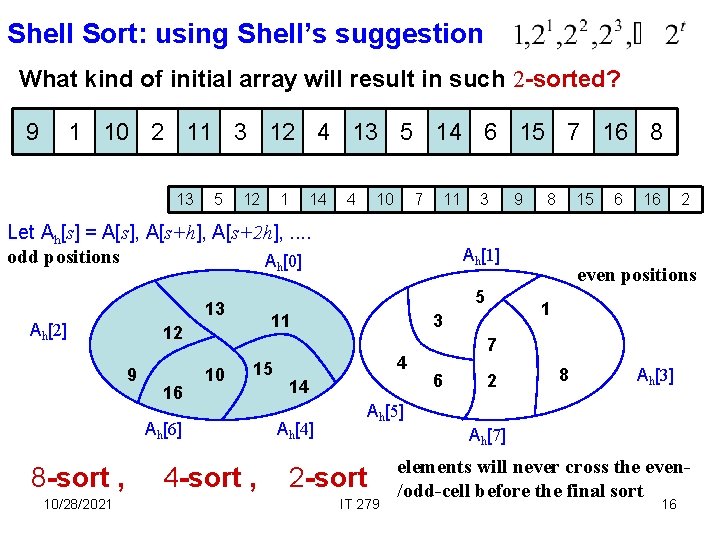
Shell Sort: using Shell’s suggestion What kind of initial array will result in such 2 -sorted? 9 1 10 2 11 3 12 4 13 5 14 6 15 7 16 8 13 5 12 1 14 4 10 7 11 Let Ah[s] = A[s], A[s+h], A[s+2 h], . . odd positions Ah[0] 11 12 9 16 10 15 Ah[6] 8 -sort , 10/28/2021 4 -sort , 9 8 15 Ah[1] 5 13 Ah[2] 3 14 16 2 even positions 1 3 4 6 7 6 2 8 Ah[3] Ah[5] Ah[4] Ah[7] 2 -sort IT 279 elements will never cross the even/odd-cell before the final sort 16

Shell sort algorithm void shellsort(int a[], int size) { int h = size/2; while (h > 0) { // h-sort for (int i=h; i<size; i++) { int t=a[i], j=i; while (j >= h && a[j-h] > t) { a[j] = a[j-h]; j -= h; } a[j]=t; } h /= 2; } // end increment } h=4 bad strategy h=4 i h=4 j-h 7 j-h 5 10/28/2021 j j, i t t j 8 14 6 12 9 j 2 IT 279 16 j 1 17

hk+1 -sorted hk+1 hk+1 hk+2 -sorted A[p] A[p-(x hk+2+y hk+1)] < A[p] If j is a liner combination of hk+2 and hk+1 with positive coefficients, then there is no need to check A[p-j] < A[p] xp+yq= gcd(p, q) if gcd(p, q) = 1, then any number is a liner combination of p and q 10/28/2021 IT 279 18

A[p-(x hk+2+y hk+1)] < A[p] hk+1 -sorted hk+1 hk+2 -sorted A[p] A[p-j] If j is a liner combination of hk+2 and hk+1 with positive coefficients, then there is no need to check A[p-j] < A[p] while (h > 0) { // h-sort for (int i=h; i<size; i++) { int t=a[i], j=i; while (j >= h && a[j-h] > t) { a[j] = a[j-h]; j -= h; } a[j]=t; } 10/28/2021 while (h > 0) { // h-sort for (int i=h; i<size; i++) { int t=a[i], j=i; while (x > j && j >= h && a[j-h] > t) { a[j] = a[j-h]; j -= h; } a[j]=t; } IT 279 19

A[p-(x hk+2+y hk+1)] < A[p] hk+1 -sorted hk+1 hk+2 -sorted A[p] A[p-j] xp+yq= gcd(p, q) If gcd(hk+1 , hk+2 ) = 1, then for sufficiently large j, we have that j is a liner combination of hk+2 and hk+1 with positive coefficients, there is no need to check A[p-j] < A[p] 10/28/2021 IT 279 20

gcd(hk+1 , hk+2 ) = 1, A[p-j] < A[p] 10/28/2021 IT 279 21

while (h > 0) { // h-sort for (int i=h; i<size; i++) { int t=a[i], j=i; while (x > j && j >= h && a[j-h] > t) { a[j] = a[j-h]; j -= h; } a[j]=t; } 10/28/2021 IT 279 22

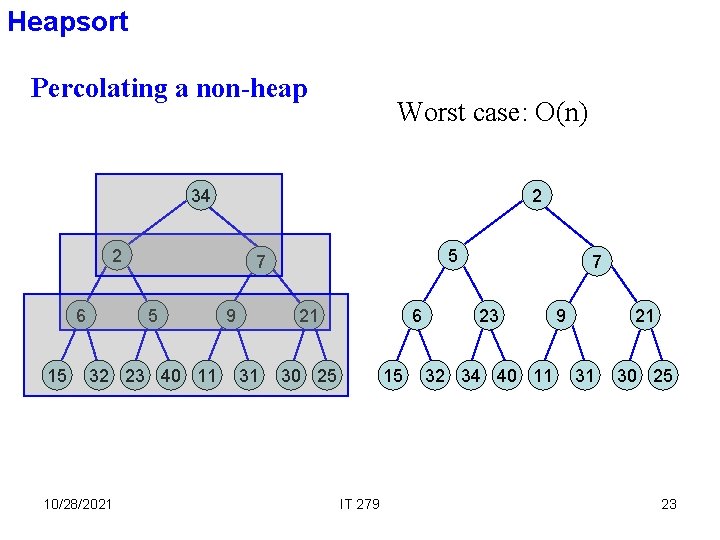
Heapsort Percolating a non-heap Worst case: O(n) 34 2 15 2 6 15 6 23 5 32 23 5 40 11 10/28/2021 5 30 7 9 25 30 21 7 31 6 21 25 30 7 15 IT 279 7 23 32 34 40 11 9 21 31 30 25 23

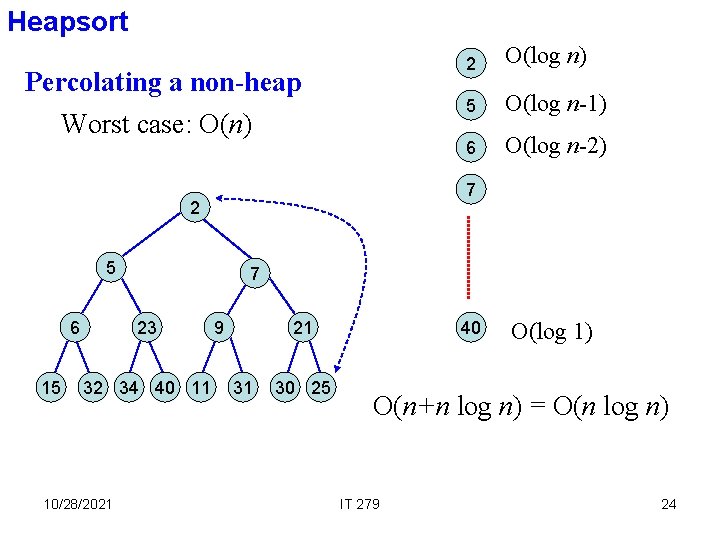
Heapsort Percolating a non-heap Worst case: O(n) 5 15 5 O(log n-1) 6 O(log n-2) 7 23 32 34 40 11 10/28/2021 O(log n) 7 2 6 2 9 21 31 30 25 40 O(log 1) O(n+n log n) = O(n log n) IT 279 24

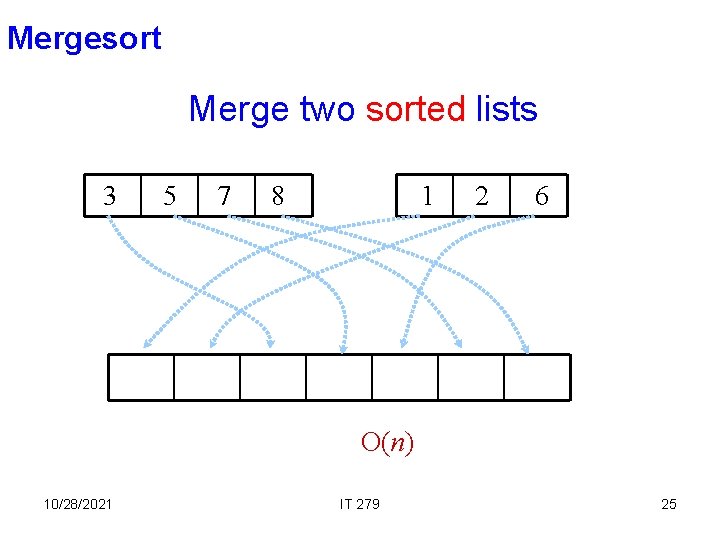
Mergesort Merge two sorted lists 3 5 7 8 1 2 6 O(n) 10/28/2021 IT 279 25

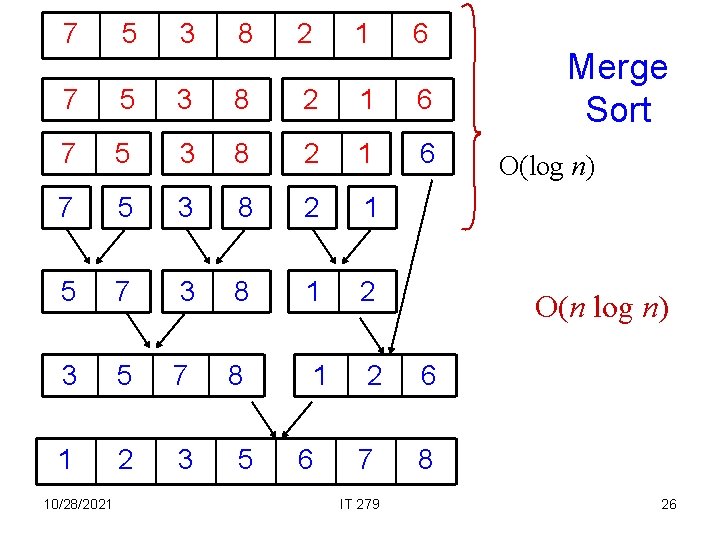
7 5 3 8 2 1 6 7 5 3 8 2 1 5 7 3 8 1 2 3 5 7 8 1 2 3 10/28/2021 5 6 7 IT 279 Merge Sort O(log n) O(n log n) 6 8 26

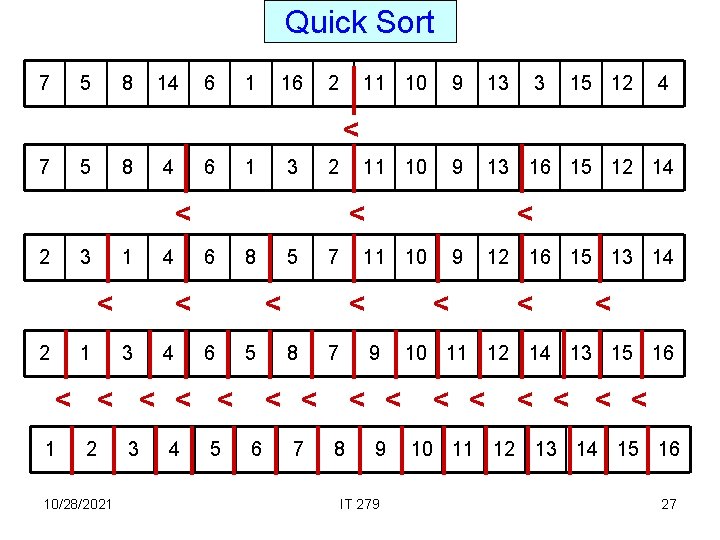
Quick Sort 7 5 8 14 6 1 16 2 11 10 9 13 3 15 12 4 11 10 9 13 16 15 12 14 < 7 5 8 4 6 1 3 2 < 2 3 1 4 < 2 1 < 6 8 < 3 4 2 10/28/2021 3 4 7 11 10 < 6 5 < < < 1 5 5 < 8 7 7 < < 8 9 < < 6 < 9 IT 279 12 16 15 13 14 < < 10 11 12 14 13 15 16 < < < 10 11 12 13 14 15 16 27

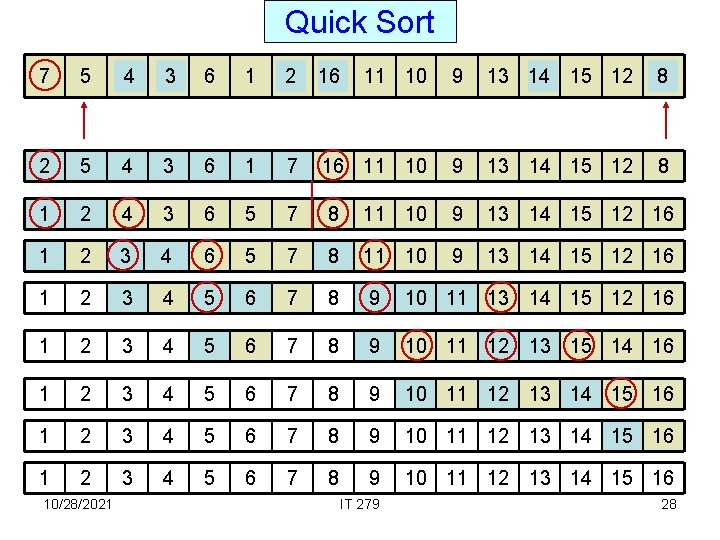
Quick Sort 7 5 84 14 3 6 1 16 2 2 16 11 10 9 13 14 3 15 12 4 8 2 5 4 3 6 1 7 16 11 10 9 13 14 15 12 8 1 2 4 3 6 5 7 8 11 10 9 13 14 15 12 16 1 2 3 4 5 6 7 8 9 10 11 12 13 15 14 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 IT 279 28 10/28/2021

/* Quick Sort */ void Swap. Two(int A[], int i, int j){ int temp = A[i]; A[i]=A[j]; A[j]=temp; } Quick Sort void Quick. Sort(int A[], int h, int t){ // h: head // t: tail if (h == t) return; int i=h+1, j=t; if (i==j) { if (A[h] > A[i]) Swap. Two(A, h, i); return; } while (i < j) { while (A[h] >= A[i] && i < t) i++; while (A[h] <= A[j] && j > h) j--; if (i < j) Swap. Two(A, i++, j--); if (i==j && A[h]>A[i]) Swap. Two(A, h, i); } Quick. Sort(A, h, i-1); Quick. Sort(A, i, t); } 10/28/2021 IT 279 29