Domain Wall Fermions and other 5 D Algorithms
















- Slides: 17

Domain Wall Fermions and other 5 D Algorithms A D Kennedy University of Edinburgh DWF@X BNL

Neuberger’s Operator 0 μ 1 All the methods that are used to put chiral fermions on the lattice are rational approximations to Neuberger’s operator They are not just analogous, there is a well-defined mapping between them A D Kennedy 2

5 D History First 5 D algorithm in LGT was Lüscher’s multiboson algorithm His multiple pseudofermions can be viewed as one 5 D pseudofermion field This led to PHMC and RHMC These are the analogous methods with 4 D pseudofermions A D Kennedy 3

Unified View of Algorithms Kernel Constraint (5 D, 4 D) Approximation Representation (CF, PF, CT=DWF) Today I will concentrate on the choice of constraint But first I want to point out that we can draw some conclusions just from the 4 D-5 D equivalence per se And I am not able to resist one brief rant about the choice of kernel A D Kennedy 4

Significance of 5 D Locality We can choose an awful approximation for which the Neuberger operator fails to be local even on smooth configurations Nevertheless, the corresponding DWF operator is manifestly local in 5 D We may thus conclude that “ 5 D locality” does not eo ipso imply physical (4 D) locality A D Kennedy 5

Reflection/Refraction Do we need “reflection/refraction” to resolve the discontinuity in the derivative of the Neuberger operator? This is more-or-less the same for 4 D or 5 D formulations MD will “see” the barrier if The rational approximation is poor enough The MD integration step-size is small enough Perhaps a good compromise is to use as poor an approximation for the MD as we can get away with, while using a good (Zolotarev? ) approximation for the MC acceptance step Does the problem manifest itself for large volumes anyway? A D Kennedy 6

Kernels Wilson (Boriçi) kernel Shamir kernel Möbius kernel A D Kennedy 7

Choice of Kernel We leave it to the following talks to discuss the merits of various choice of kernel We just observe that the choice of a kernel with a non-trivial denominator inhibits many useful algorithmic techniques E. g. , the user of a nested inner-outer CG solver with an inner multishift (to implement the rational approximation in partial fraction form) and an outer multishift (to implement multiple partially quenched valence masses With the Shamir kernel this requires three levels of nesting A D Kennedy 8

Schur Complement The Neuberger operator is intrinsically a non-linear function of its Dirac operator kernel It is a function of two non-commuting 4 D operators We may write it as a linear operator by introducing an extra dimension The size of the fifth dimension is just the degree of the rational approximation used To be precise, Ls = # poles The basic idea is that the 4 D operator is the Schur complement of the 5 D operator A D Kennedy 9

Schur Complement Consider the block matrix It may be block diagonalised by an LDU factorisation (Gaussian elimination) The bottom right block is the Schur complement A D Kennedy 10

4 D Pseudofermions So, what can we do with the Neuberger operator represented as a Schur complement? Consider the five-dimensional system of linear equations The bottom four-dimensional component is A D Kennedy 11

5 D Pseudofermions Alternatively, introduce a five-dimensional pseudofermion field Then the pseudofermion functional integral is So we also introduce n-1 Pauli-Villars fields and we are left with just det Dn, n = det DN A D Kennedy 12

Disadvantages of 5 D pseudofermions Introduce extra noise into the 4 D world Letting the 5 D pseudofermions cancel stochastically with their Pauli-Villars partners (“pseudo-fermions”) is a very bad idea Cancelling them explicitly is better, but one is still has Ls-1 unnecessary noisy estimators of 1 These increase the maximum force on the 4 D gauge fields and force the MD integration step-size to be smaller A D Kennedy 13

Disadvantages of 5 D pseudofermions Extent of the fifth dimension is fixed At least over an entire HMC trajectory With 4 D pseudofermions one can adjust the degree of the rational approximation at each MD step to cover the spectrum of the kernel with fixed maximum error A D Kennedy 14

Disadvantages of 4 D Pseudofermions Cannot evaluate roots of Neuberger operator We cannot use the multishift solver techniques used with 5 D pseudofermions because we would need constant shifts of the 4 D operator and not the 5 D one Not obvious how to implement odd number of flavours efficiently with 4 D pseudofermions Not obvious how to use nth root RHMC acceleration trick But we can still use Hasenbusch’s technique These techniques can be implemented using nested 4 D CG solver with multishift on both inner and outer solvers A D Kennedy 15

Desiderata & Conclusions It would be nice to make progress in the following areas Express nth roots of Neuberger operator as a 5 D system Work out how to systematically improve the condition number of 5 D systems The Schur complement of a 5 D system is uniquely defined, but there are many 5 D matrices with the same Schur complement With each class of such 5 D matrices it is often possible to greatly change the condition number by fairly simple transformations It would be nice to know how to do this systematically The evidence at present indicates that better approximations (e. g. , Zolotarev rather than tanh) are not intrinsically worse conditioned A D Kennedy 16

Questions? A D Kennedy 17
 Heavy fermions
Heavy fermions Pauli blocking of light scattering in degenerate fermions
Pauli blocking of light scattering in degenerate fermions Fermions obeys
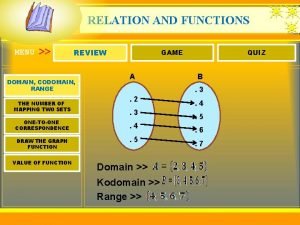
Fermions obeys Domain co domain and range of a relation
Domain co domain and range of a relation Data domain fundamentals
Data domain fundamentals A_______ bridges the specification gap between two pls.
A_______ bridges the specification gap between two pls. Mary dahlgren sound walls
Mary dahlgren sound walls Chris brown wall
Chris brown wall T junction of stretcher bond
T junction of stretcher bond Members used to carry wall loads over wall openings
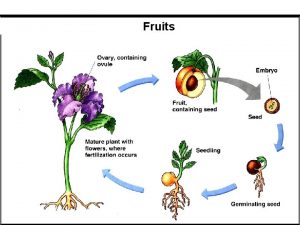
Members used to carry wall loads over wall openings The wall of ovary develops into wall of fruit called
The wall of ovary develops into wall of fruit called A painting or other work of art executed directly on a wall
A painting or other work of art executed directly on a wall Z domain to frequency domain
Z domain to frequency domain Z transform time reversal
Z transform time reversal Z transform online
Z transform online Domain specific vs domain general
Domain specific vs domain general Domain specific software engineering
Domain specific software engineering Problem domain vs knowledge domain
Problem domain vs knowledge domain