Domain and Range from Graphs Domain and Range

Domain and Range from Graphs

Domain and Range Sometimes you list specific values when the data is from: table ordered pairs discrete graphs mapping some word problems Sometimes you describe the possible values when the data is from: continuous graphs some word problems Today we will focus more on domain and range from graphs Discrete Graphs: list xs and ys Continuous graphs: describe the intervals or ranges of x and y values shown on the graph. Sometimes using inequalities, sometimes using words *Think: Does it go on forever in a certain direction? Does it have a start and stop, or a min. and max? Check for open or closed circles on the end

Continuous graphs: describe the possible values Domain = describe x values, inputs *tip – think does this function go “right and left forever”? if Yes, the xs can be “all real numbers” if No, describe what x values are shown with an inequality. ie x>2 or -3<x<2 Range = describe y values, outputs *tip - think does this function go “up and down forever”? if Yes, the ys can be “all real numbers” if No, describe what y values are shown with an inequality Domain: {All real numbers} Domain: {-6 < x < 7} Range: {All real numbers} Range: {y < 5} Range: {-2 < y < 4}

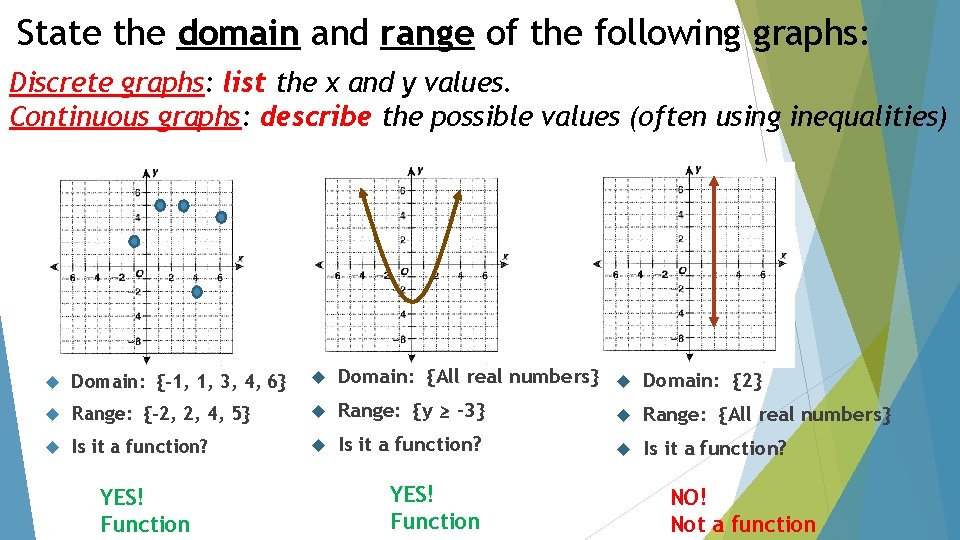
State the domain and range of the following graphs: Discrete graphs: list the x and y values. Continuous graphs: describe the possible values (often using inequalities) Domain: {-1, 1, 3, 4, 6} Domain: {All real numbers} Domain: {2} Range: {-2, 2, 4, 5} Range: {y ≥ -3} Range: {All real numbers} Is it a function? YES! Function NO! Not a function

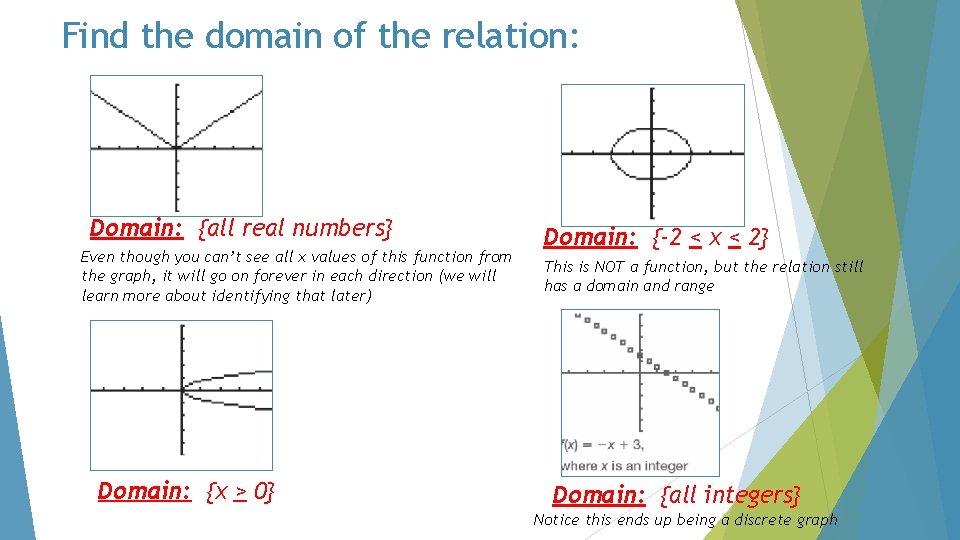
Find the domain of the relation: Domain: {all real numbers} Even though you can’t see all x values of this function from the graph, it will go on forever in each direction (we will learn more about identifying that later) Domain: {x > 0} Domain: {-2 < x < 2} This is NOT a function, but the relation still has a domain and range Domain: {all integers} Notice this ends up being a discrete graph

Identify the dependent and independent quantities Pedro is hiking in a canyon. At the start of his hike, he was at 3500 feet. During the first 20 minutes of the hike, he descended 500 feet at a constant rate. Then he rested for half an hour before continuing the hike at the same rate. The independent quantity is time (how long he has been hiking) Time will be graphed on the x axis Domain {0 < x < 100} The dependent quantity is the elevation (because his elevation depends on how long he has hiked) Elevation Range will be graphed on the y axis {1225 < y < 3500}