Does the order of the horizontal and vertical

Does the order of the horizontal and vertical transforms matter in the representation of an operational static covariance model in global atmospheric DA? Marek Wlasak and Mike Cullen © Crown copyright Met Office

Outline Give the argument for and properties of swapping the order of the vertical and horizontal transforms in the static covariance model. Show benefits of swapped order Summarise

Argument and properties for swapping the order of the horizontal and vertical transforms © Crown copyright Met Office

Static covariances are still important • Hybrid DA methods rely on a static covariance model (Bs) to give sufficient degrees of freedom. • Static part still contributes to over 50% of the whole forecast error. This is not going to change much in the near future unless there is a huge increase in the number of ensemble members used. (Reference: Hidden Error Variance Theory, Bishop 2013) • So modelling of static covariances is important.

Rationale for conserving the properties of the training data • We need to calibrate a covariance model with training data from an ensemble properly representing the forecast error. • Ideally we would like to get to a position where the covariance model conserves some key properties and the implied background error covariance faithfully represents the training data. • This philosophy should in the long run help in bootstrapping to provide a good covariance file. • It also means that the emphasis moves away from tuning a covariance model, to getting the training data right.

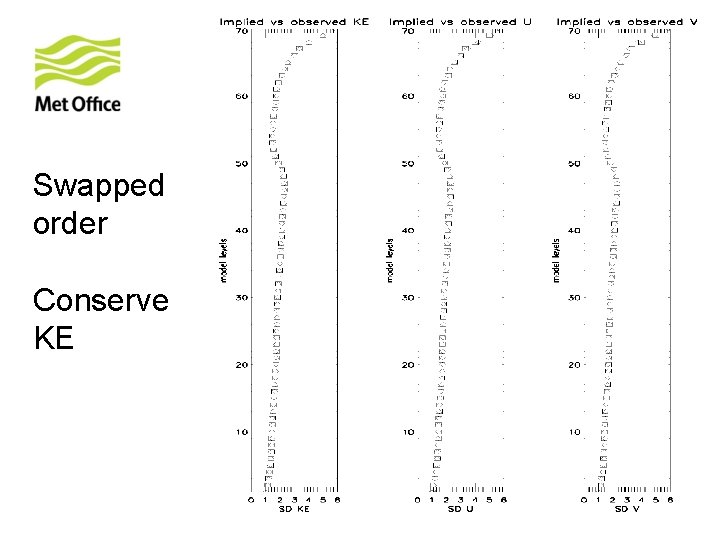
Conservation of variance • The total kinetic energy on each vertical level is determined by : • the power spectra of the stream-function ψ’ and velocity potential χ’. ( It holds variance and gradient information. ) • If the power spectra of ψ’, χ’ are conserved so will the total kinetic energy. • This will have a knock on effect on horizontal length scales of the balanced pressure and temperature.

Background covariance structure. • Tv. Th. Tp (swapped) • Th. Tv. Tp (current) • Latitude dependence built into parameter transform only. • Latitude dependence built into vertical and parameter transform. • Global variances and power spectra of model variables conserved. • Power spectra not conserved for model variables.

Results: Background error covariance comparison © Crown copyright Met Office

Swapped order Conserve KE

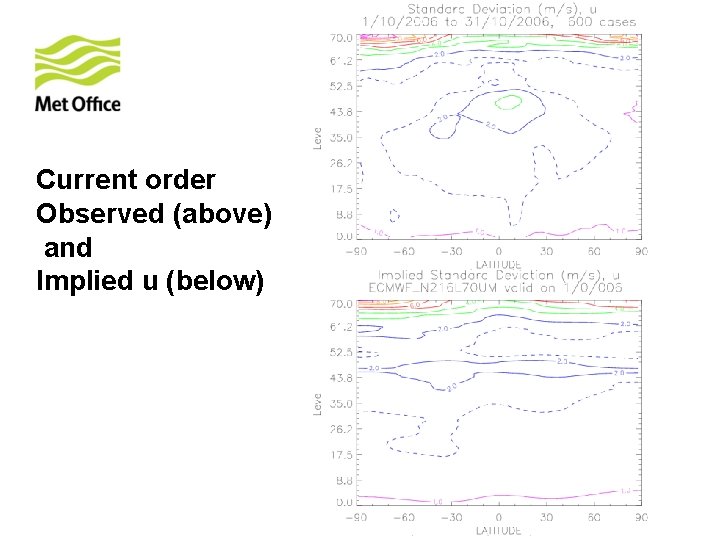
Current order Observed (above) and Implied u (below)

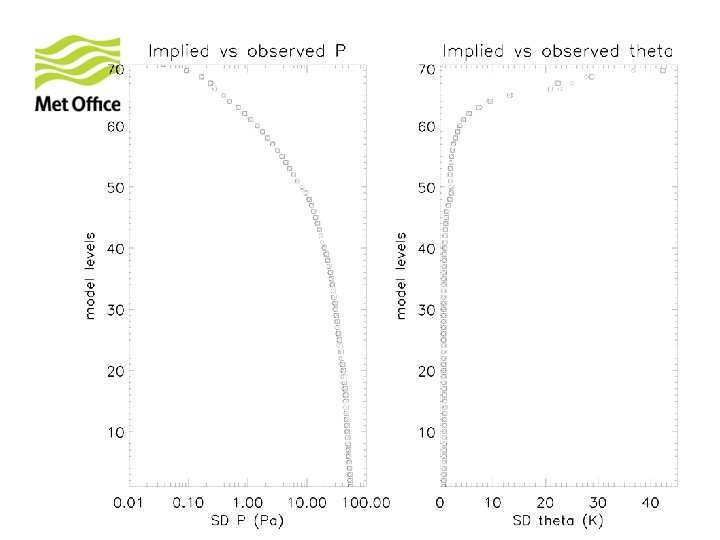
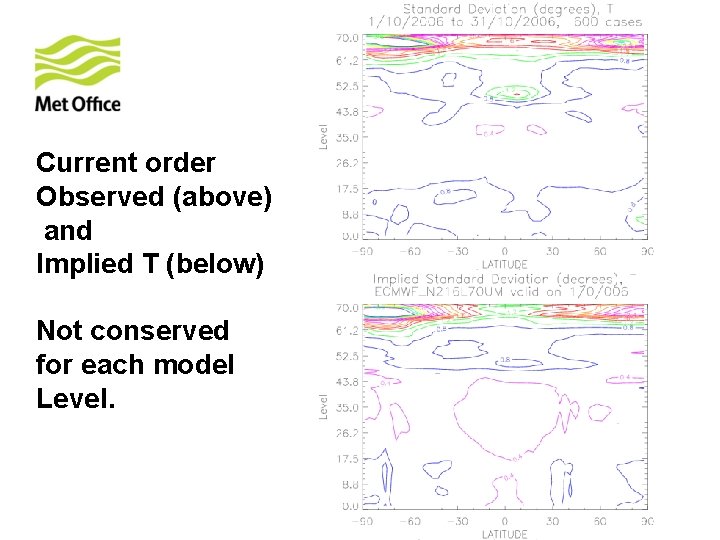
Current order Observed (above) and Implied T (below) Not conserved for each model Level.

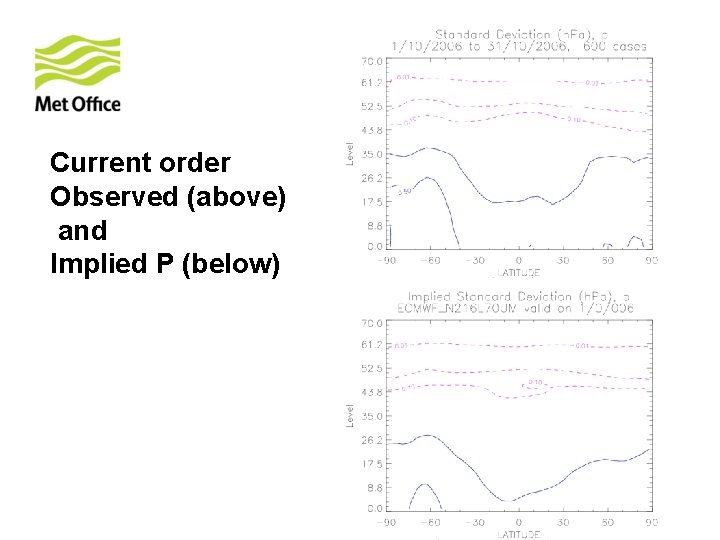
Current order Observed (above) and Implied P (below)

Trial results © Crown copyright Met Office

Non-hybrid trials Two trials were run with UM at N 320 and VAR at N 216 and N 108. The main difference is seen with an increase in the size of theta and pressure increments, due to the increase in associated background errors. There is also an increase horizontal length scale in pressure and theta.

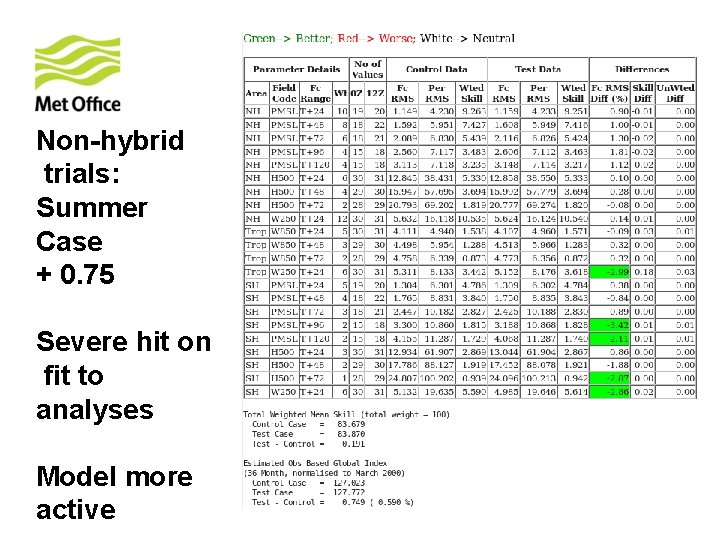
Non-hybrid trials: Summer Case + 0. 75 Severe hit on fit to analyses Model more active

Non-hybrid trials: Winter Case Fit to obs + 1. 2

Summary: • It is clear that swapping the transform order has a big effect on results when tested without the flow dependence of the hybrid. Neutral results have so far been obtained in hybrid trials. • The biggest benefit is that the background error is now represented by the training data. It is expected that an improved choice of training data, consistent with the hybrid error modes, will help.

Additional slides. © Crown copyright Met Office

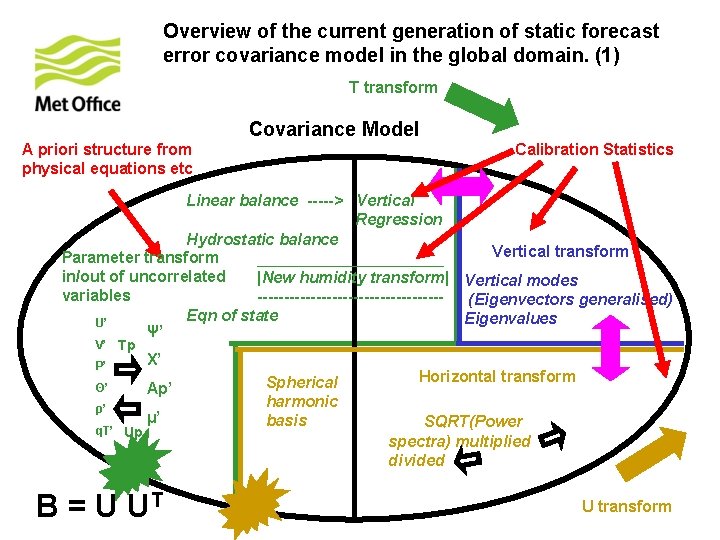
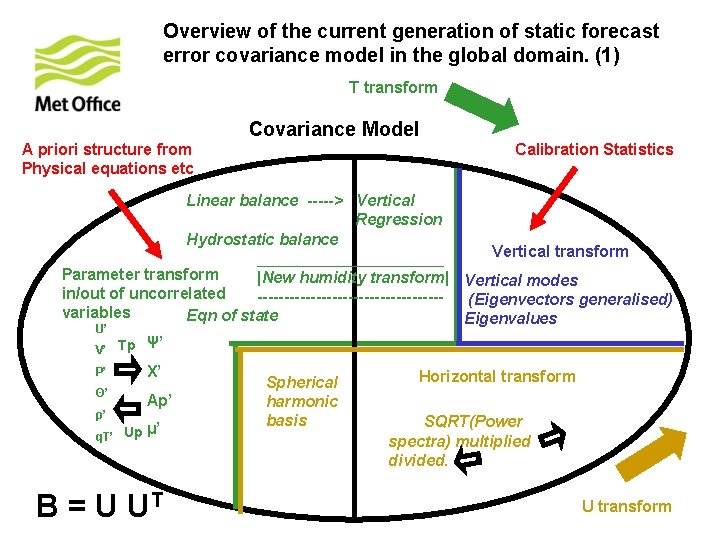
Overview of the current generation of static forecast error covariance model in the global domain. (1) T transform Covariance Model A priori structure from physical equations etc Calibration Statistics Linear balance -----> Vertical Regression Hydrostatic balance Vertical transform Parameter transform ___________ in/out of uncorrelated |New humidity transform| Vertical modes variables -----------------(Eigenvectors generalised) Eqn of state Eigenvalues U’ Ψ’ V’ Tp P’ Χ’ Θ’ Ap’ ρ’ μ’ q. T’ Up B = U UT Spherical harmonic basis Horizontal transform SQRT(Power spectra) multiplied divided U transform

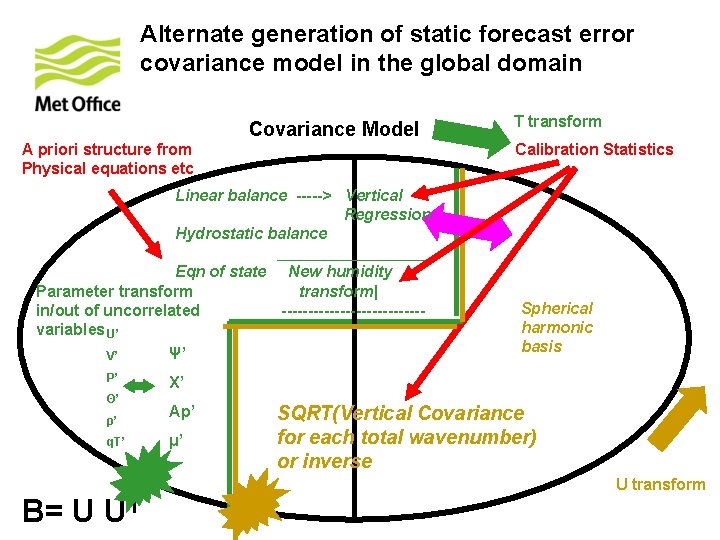
Alternate generation of static forecast error covariance model in the global domain Covariance Model A priori structure from Physical equations etc Calibration Statistics Linear balance -----> Vertical Regression Hydrostatic balance _________ Eqn of state New humidity transform| Parameter transform -------------in/out of uncorrelated variables U’ Ψ’ V’ P’ Θ’ ρ’ q. T’ T transform Spherical harmonic basis Χ’ Ap’ μ’ SQRT(Vertical Covariance for each total wavenumber) or inverse U transform B= U UT

Background covariance structure. • The static covariance model is an approximation to the true forecast error covariance B and is constructed by making a number of prior assumptions. • One choice is the order of the horizontal Uh and vertical transforms (as they do not commute). i. e. (whether the vertical transform is applied in spectral space or not. ) Ie. B 1 = Up. Uv. Uh (Up. Uv. Uh)T /= Up. Uhv (Up. Uhv)T = B 2 Where : • Up is the parameter transform • Uh is the horizontal transform • Uv is the vertical transform is grid-point space. • Uhv is the vertical transform is done in spectral space.

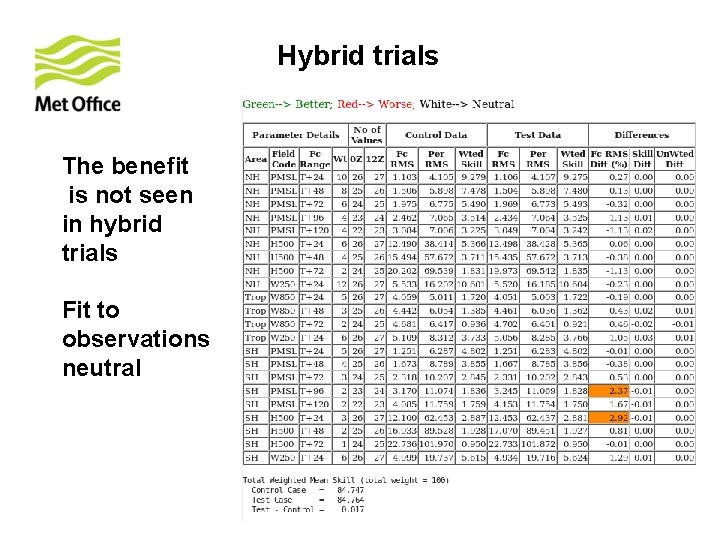
Hybrid trials The benefit is not seen in hybrid trials Fit to observations neutral

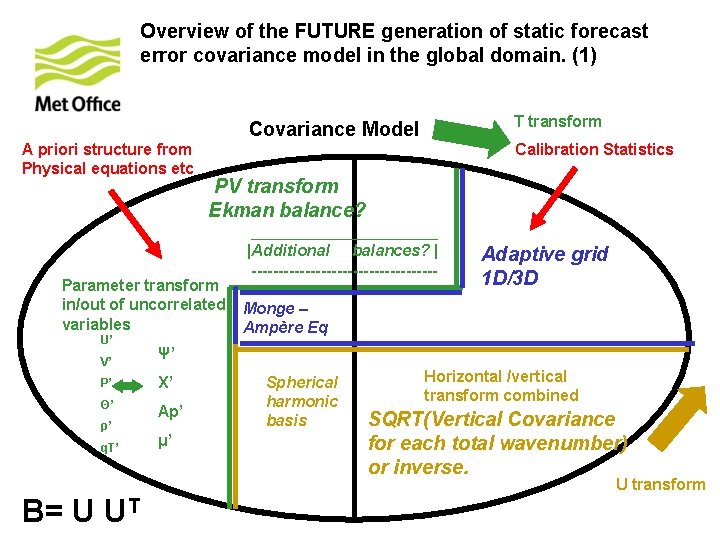
Overview of the FUTURE generation of static forecast error covariance model in the global domain. (1) T transform Covariance Model A priori structure from Physical equations etc Calibration Statistics PV transform Ekman balance? Parameter transform in/out of uncorrelated variables U’ V’ Ψ’ P’ Χ’ Θ’ Ap’ ρ’ q. T’ μ’ ___________ |Additional balances? | ------------------ Adaptive grid 1 D/3 D Monge – Ampère Eq Spherical harmonic basis Horizontal /vertical transform combined SQRT(Vertical Covariance for each total wavenumber) or inverse. U transform B= U UT

Basic overview. • Code comprises of a number of small Fortran programs being called from ksh scripts • Most important script for the user is the Launcher script. • Expect all switches that the non-developer uses to be accessed from there. • Glue between modules • Environment variables some from Launcher • Net. CDF files – including its header • Small text files that give the paths to groups of Net. CDF files.

Basic overview. • Code comprises of a number of small Fortran programs being called from ksh scripts • Most important script for the user is the Launcher script. • Expect all switches that the non-developer uses to be accessed from there. • Glue between modules • Environment variables some from Launcher • Net. CDF files – including its header • Small text files that give the paths to groups of Net. CDF files.

Future Directions in Global © Crown copyright Met Office

Overview of the current generation of static forecast error covariance model in the global domain. (1) T transform Covariance Model A priori structure from Physical equations etc Calibration Statistics Linear balance -----> Vertical Regression Hydrostatic balance Vertical transform ___________ Parameter transform |New humidity transform| Vertical modes in/out of uncorrelated -----------------(Eigenvectors generalised) variables Eqn of state Eigenvalues U’ Ψ’ V’ Tp P’ Χ’ Θ’ Ap’ ρ’ μ’ q. T’ Up B = U UT Spherical harmonic basis Horizontal transform SQRT(Power spectra) multiplied divided. U transform

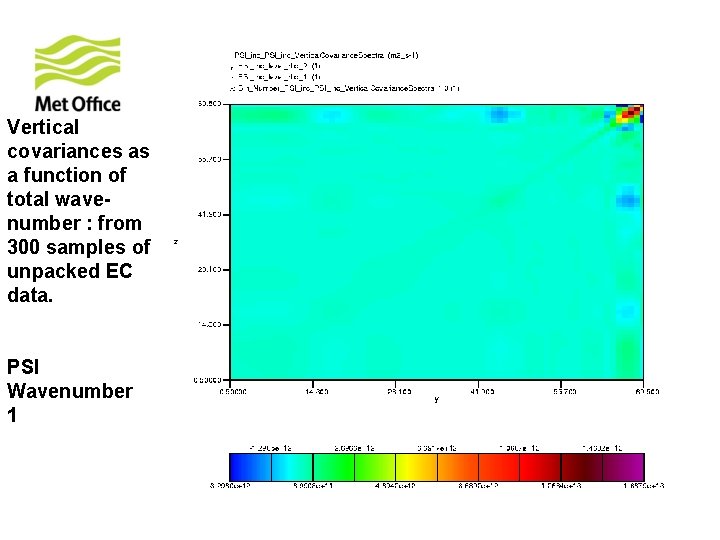
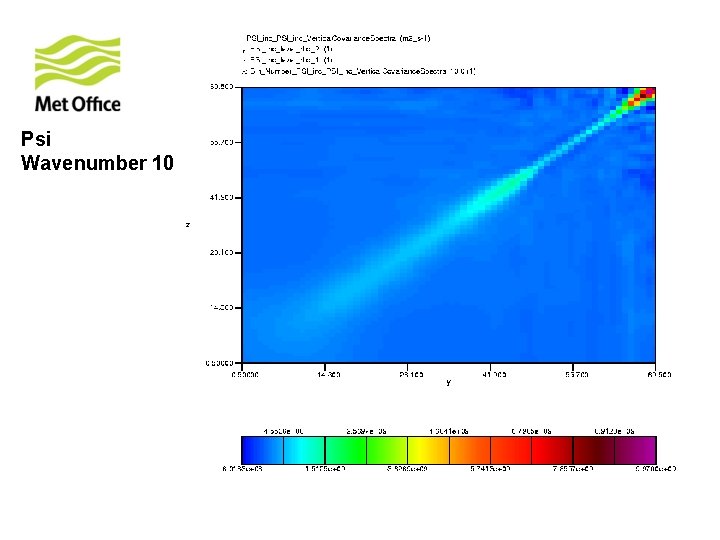
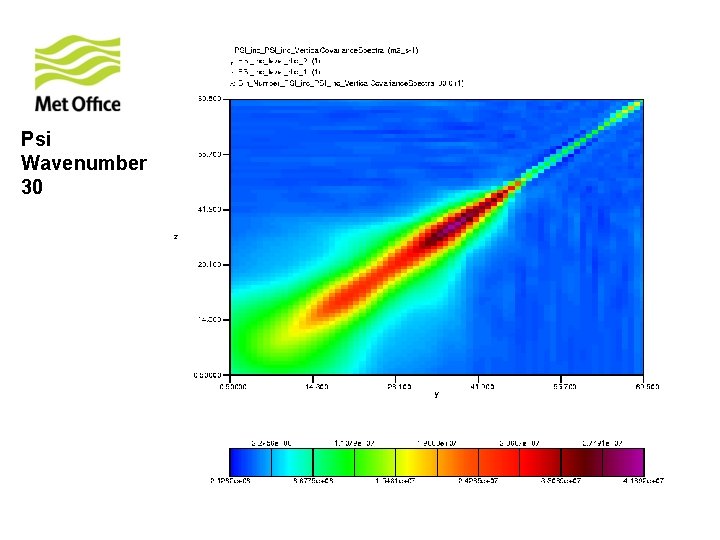
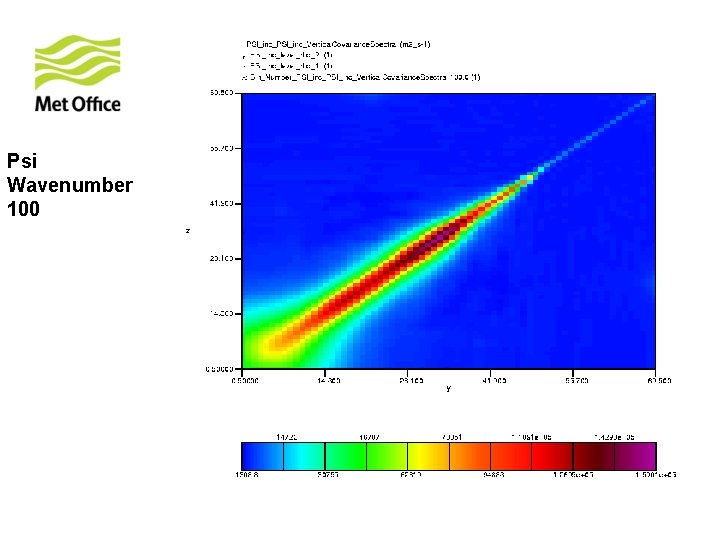
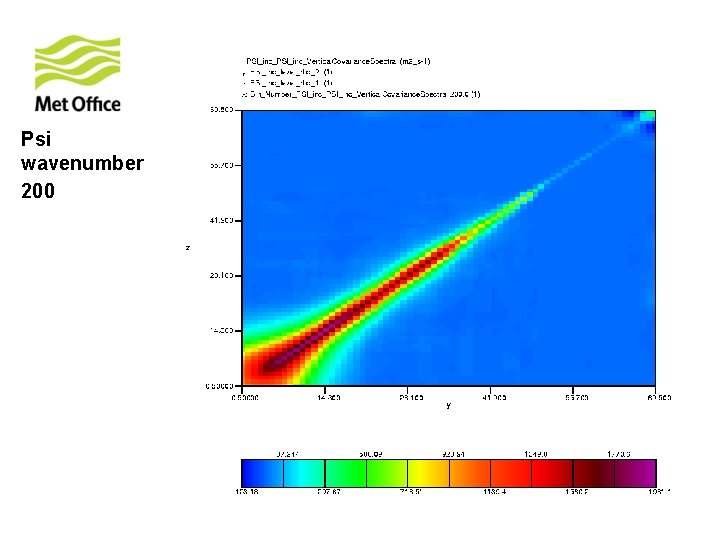
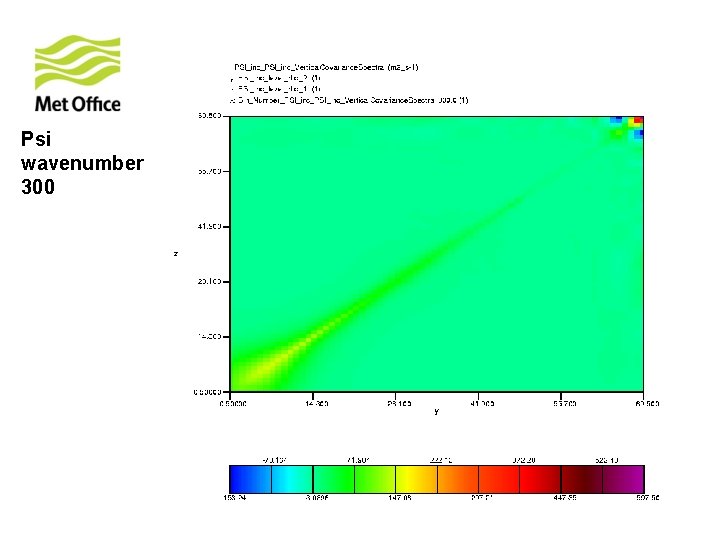
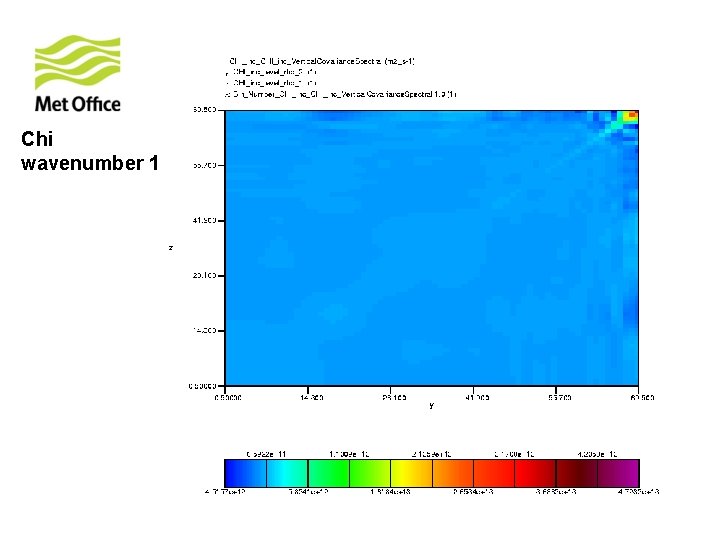
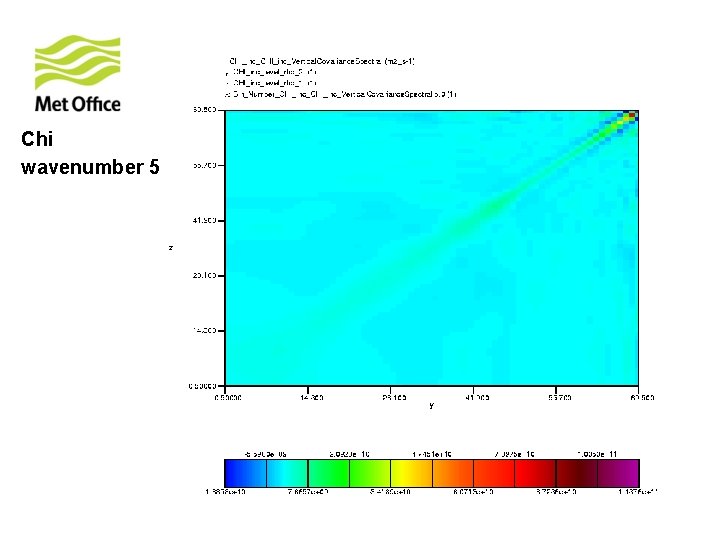
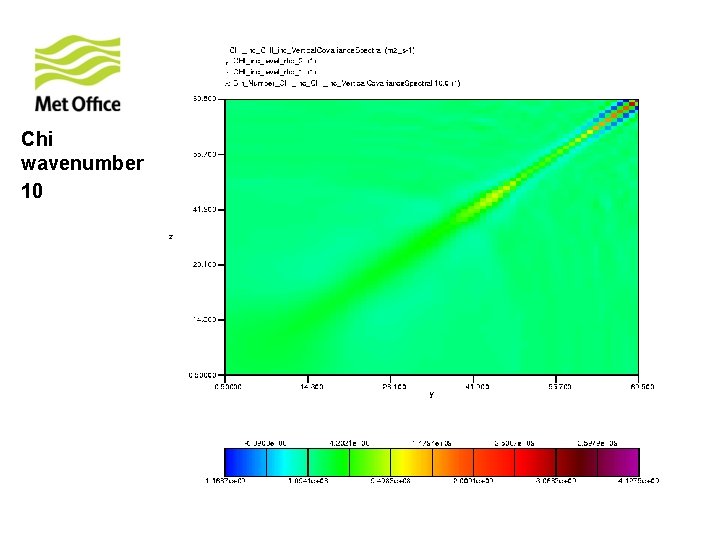
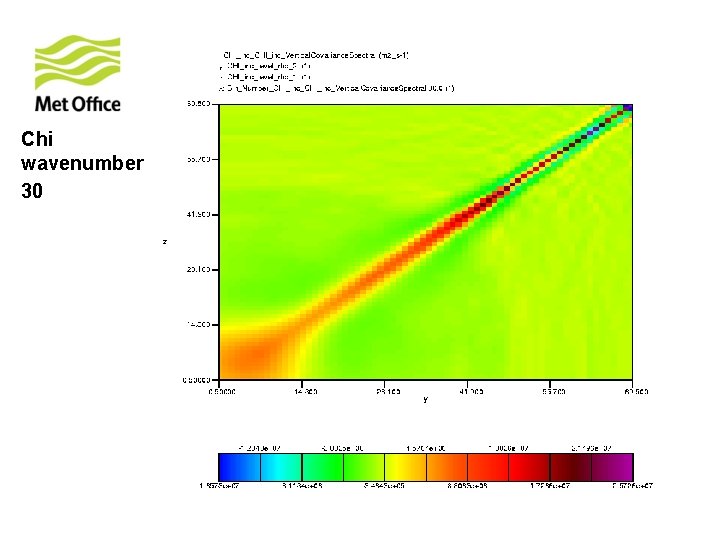
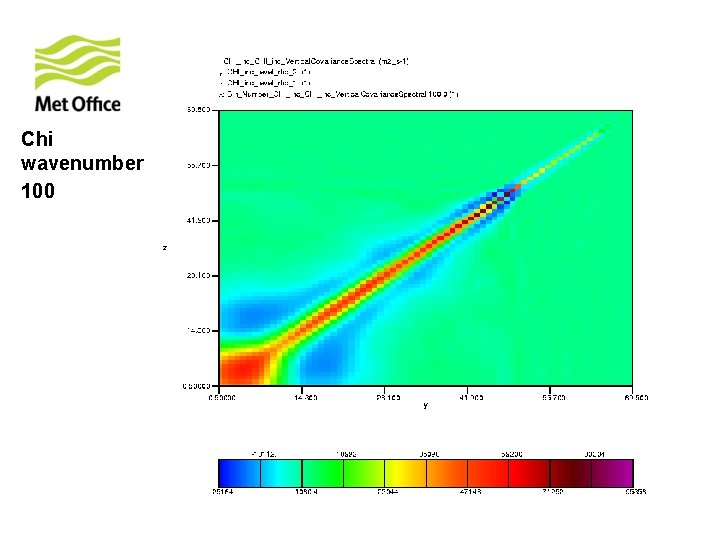
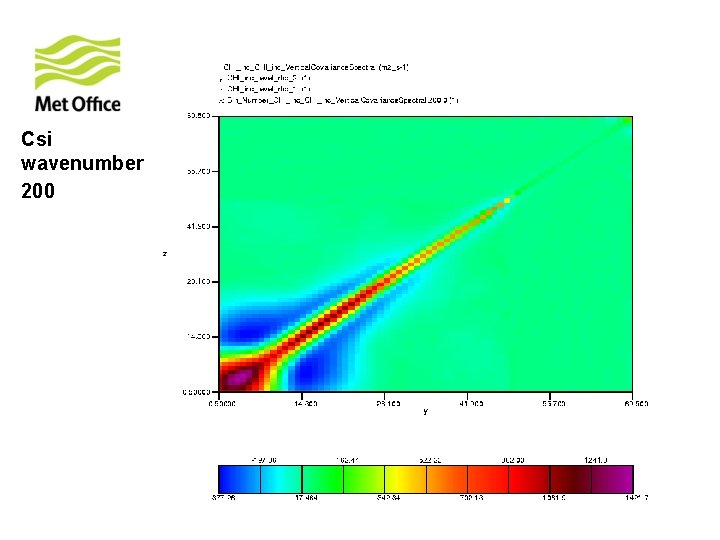
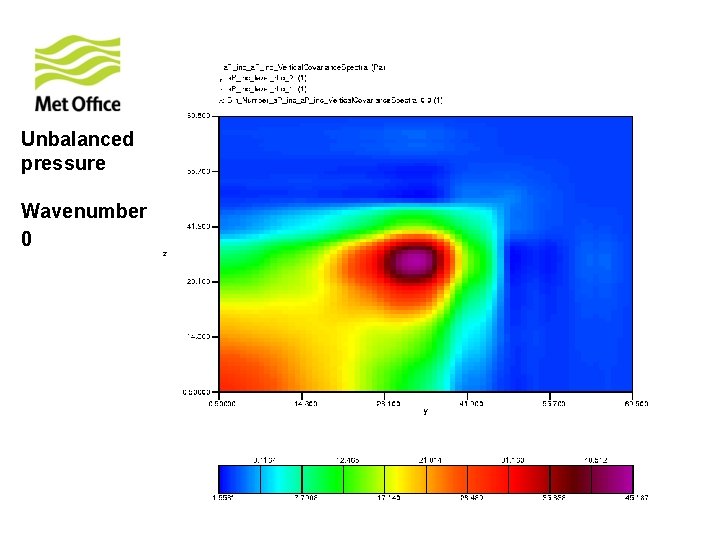
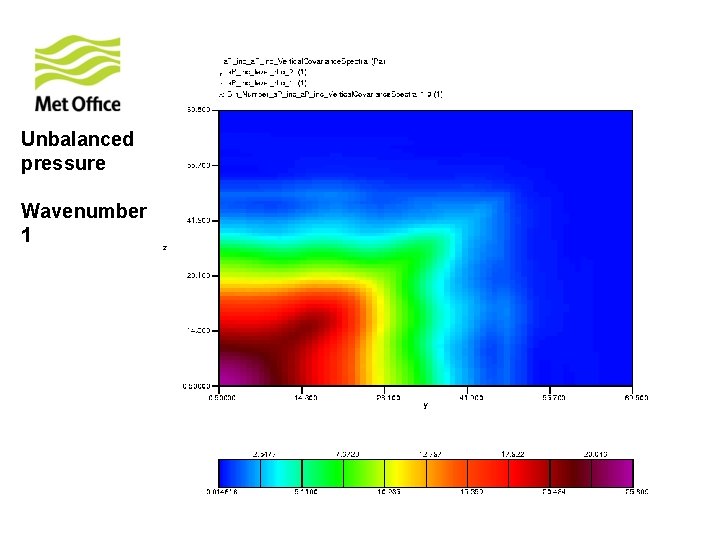
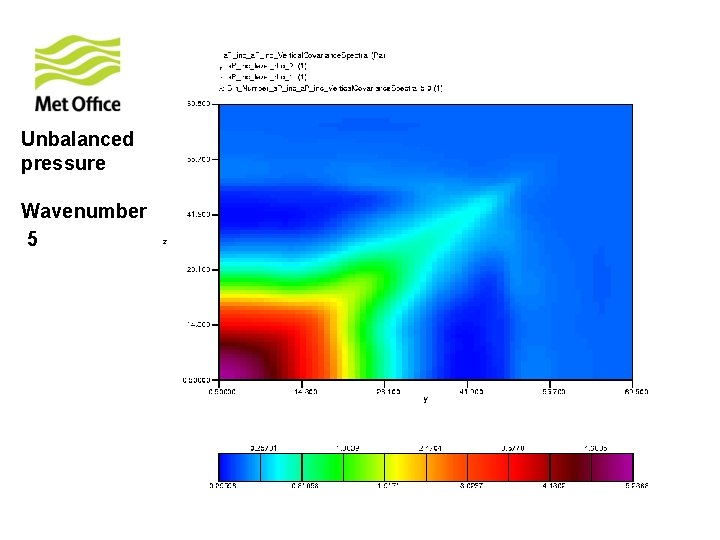
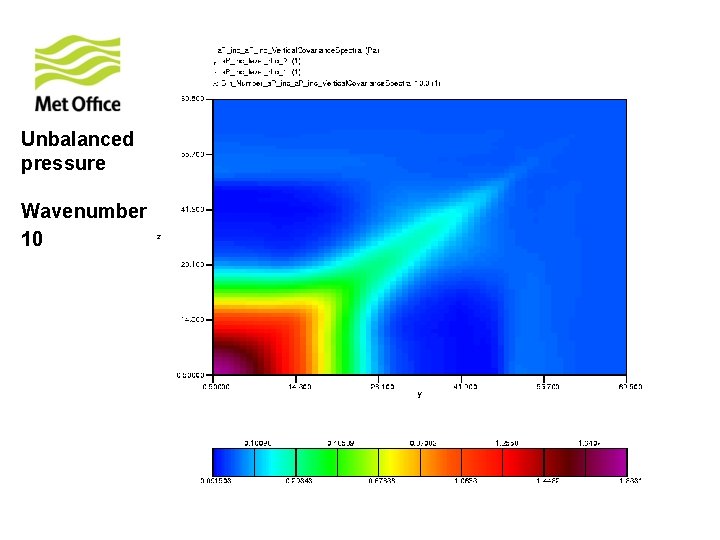
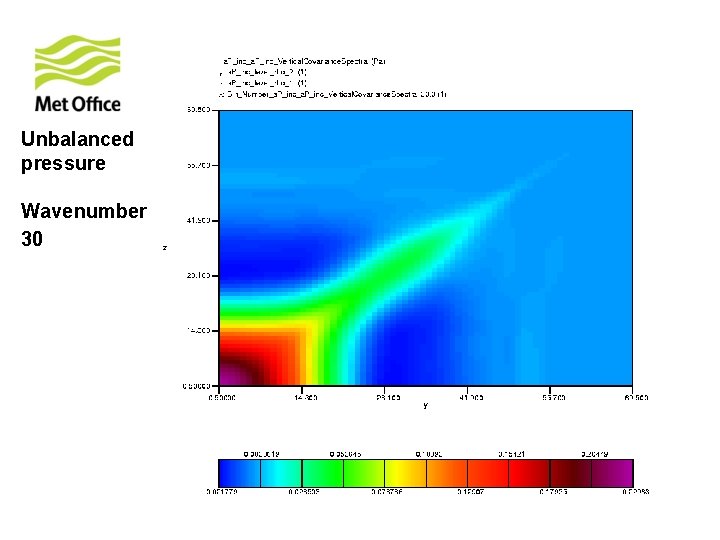
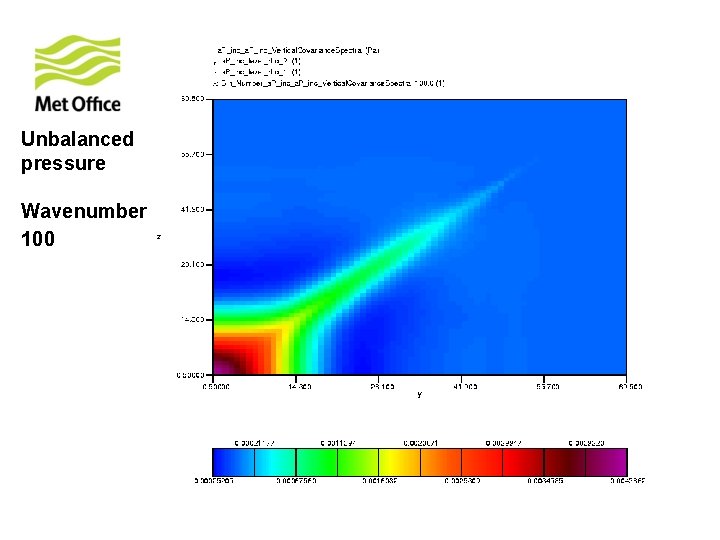
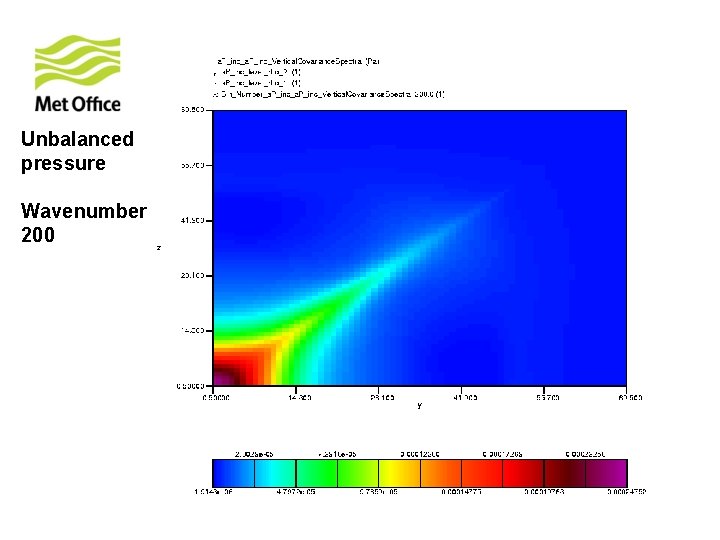
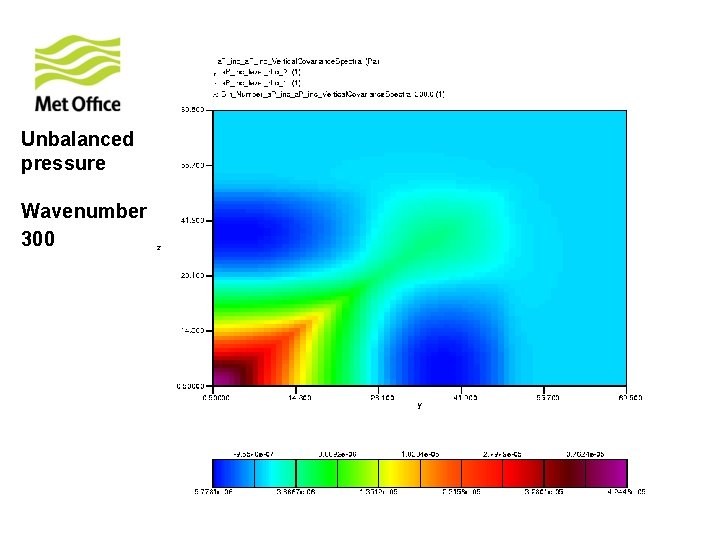
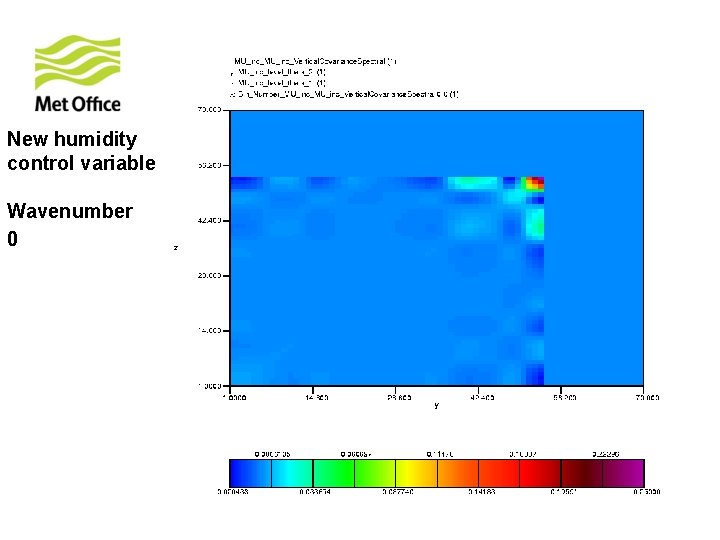
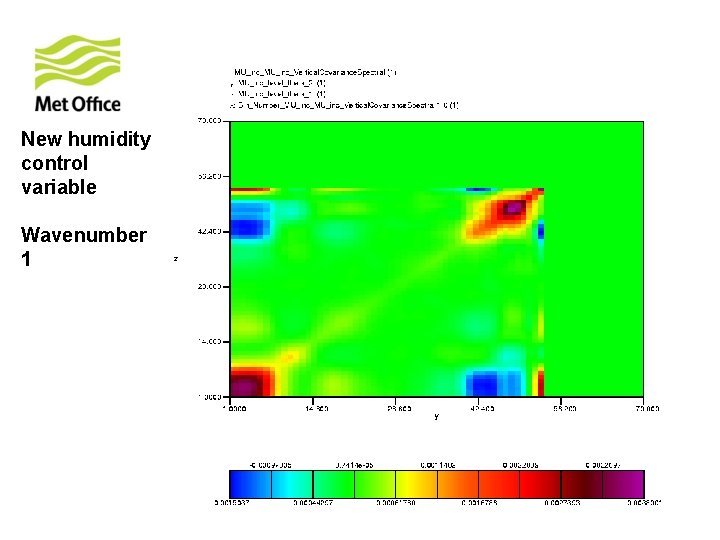
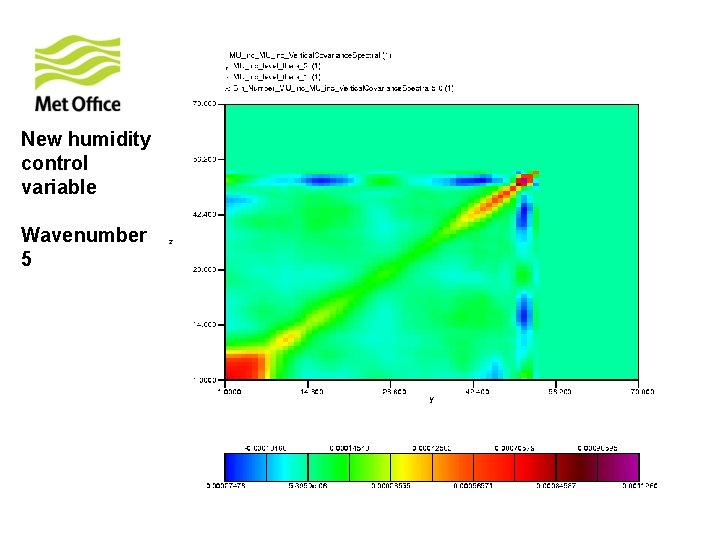
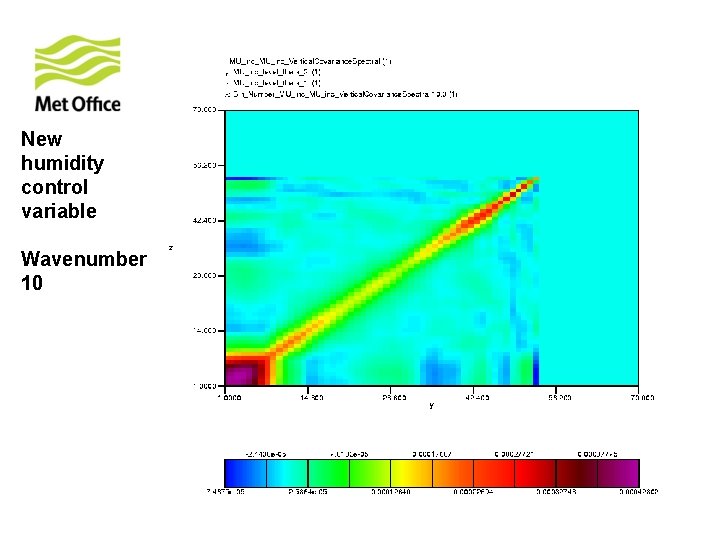
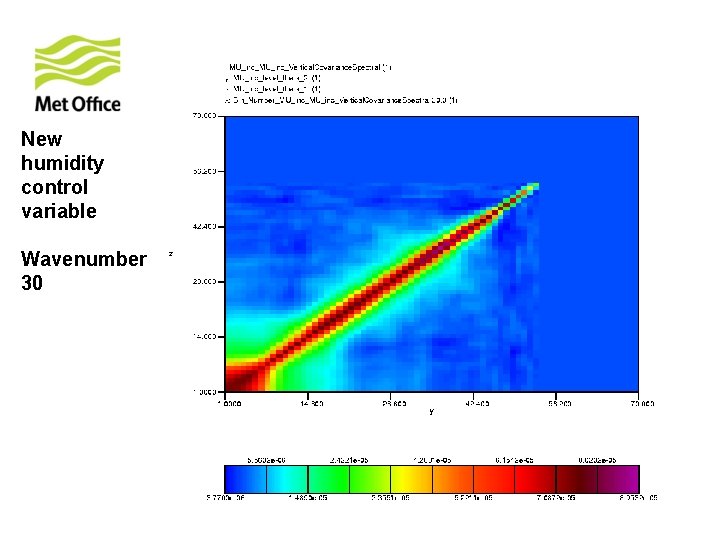
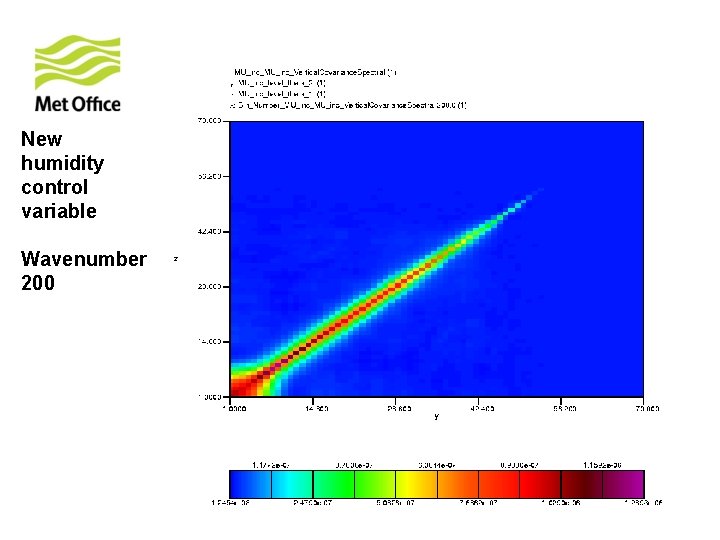
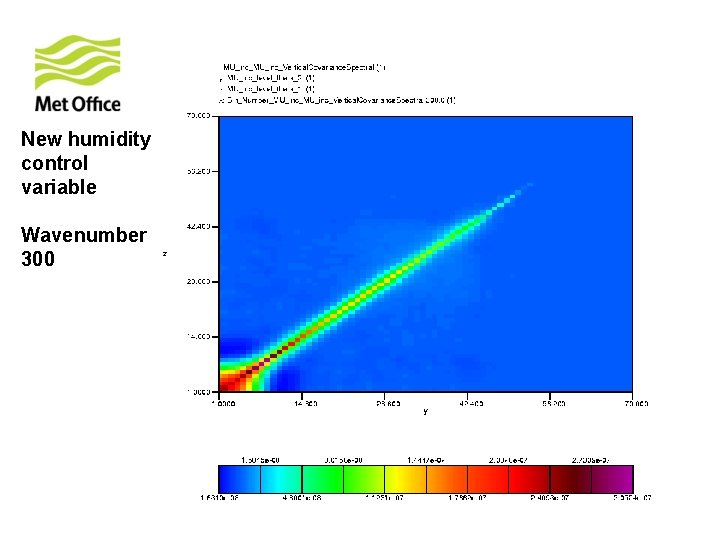
To show vertical structure is a function of horizontal total wavenumber. Look at the vertical covariances of control variables for specific horizontal total wavenumber from 300 samples of unpacked ECMWF forecast differences.

Vertical covariances as a function of total wavenumber : from 300 samples of unpacked EC data. PSI Wavenumber 1

Psi Wavenumber 5

Psi Wavenumber 10

Psi Wavenumber 30

Psi Wavenumber 100

Psi wavenumber 200

Psi wavenumber 300

Chi wavenumber 1

Chi wavenumber 5

Chi wavenumber 10

Chi wavenumber 30

Chi wavenumber 100

Csi wavenumber 200

Csi wavenumber 300

Unbalanced pressure Wavenumber 0

Unbalanced pressure Wavenumber 1

Unbalanced pressure Wavenumber 5

Unbalanced pressure Wavenumber 10

Unbalanced pressure Wavenumber 30

Unbalanced pressure Wavenumber 100

Unbalanced pressure Wavenumber 200

Unbalanced pressure Wavenumber 300

New humidity control variable Wavenumber 0

New humidity control variable Wavenumber 1

New humidity control variable Wavenumber 5

New humidity control variable Wavenumber 10

New humidity control variable Wavenumber 30

New humidity control variable Wavenumber 100

New humidity control variable Wavenumber 200

New humidity control variable Wavenumber 300