Dobr otzky Ph Dr Kateina Janakov Ph D

Dobré otázky Ph. Dr. Kateřina Jančaříková, Ph. D.

Dobré otázky jako metoda • Vychází z didaktiky matematiky, autorů Sullivana a Lilburnové. • U nás jsou to například Jančařík, Jančaříková, Novotná (2012), kteří metodu začlali rozšiřovat na didaktiku přírodních věd.

Jaké otázky klade učitel? • Otázky, které klade učitel dětem, žákům či studentům, můžeme rozdělit do dvou kategorií, na otevřené a uzavřené. • Uzavřené otázky vyžadují obvykle odpovědi, které se odvolávají na paměť, požadují od studentů např. opakovat nějaký postup nebo zopakovat fakt. • Otevřené otázky vyžadují, aby studenti více přemýšleli a aby předložili odpovědi, které se neomezí na odvolání se na fakt nebo opakování postupu. Zcela specifický typ otevřených otázek nazýváme dobrými otázkami.

Dobrá x běžná otázka • Tuto terminologii používají didaktici. • Dobrou otázkou je myšlena taková otázka, která provokuje žáky a studenty k přemýšlení, činnosti, kreativitě a vlastnímu bádání. • Naopak běžné otázky jsou otázkami uzavřenými, takové, na něž lze odpovědět jednoznačně. Záměrně nebo i nezáměrně ověřují věcné znalosti studenta (student na ně buď odpověď zná, nebo ne).

Dobrá otázka • vyžaduje víc než jen odvolání se na známá fakta, • umožní dětem, žákům a studentům, aby se něco dozvěděli, když na ni hledají odpověď, • umožňuje učiteli, aby se dozvěděl něco o žácích z odpovědí, které vysloví, • existuje na ni více odpovědí, které lze přijmout jako správné odpovědi = je možné za správnou odpověď pochválit více dětí, žáků či studentů.

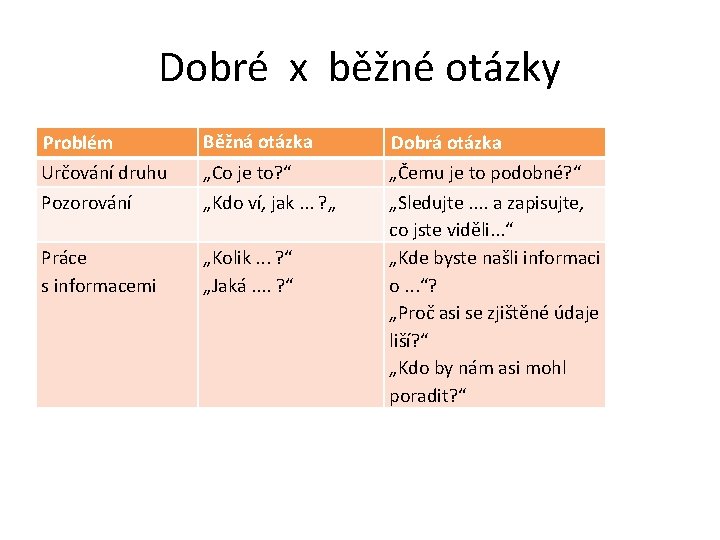
Dobré x běžné otázky Problém Běžná otázka Dobrá otázka Určování druhu Pozorování „Co je to? “ „Kdo ví, jak. . . ? „ Práce s informacemi „Kolik. . . ? “ „Jaká. . ? “ „Čemu je to podobné? “ „Sledujte. . a zapisujte, co jste viděli. . . “ „Kde byste našli informaci o. . . “? „Proč asi se zjištěné údaje liší? “ „Kdo by nám asi mohl poradit? “

Nadužívání běžných otázek v českých školách • Výklad doprovází učitelé kladením běžných otázek, např. „Jak se jmenuje tato rostlina? “, které doprovází otázky „Kdo první odpoví na otázku? “, „Kdo první vypočítá? “. • Často navíc učitel odměňuje (slovní pochvala, hvězdička, bonbón, jednička) děti či žáky, kteří jako první vyřknou správnou odpověď. • Děti a žáky k tomu, že si osvojují „vítězné strategie chování“ (mumlání, rychlé volání zcela nepromyšlených odpovědí – pokus se strefit za každou cenu atd. ), které jim umožňují zažít úspěch, ale které brání procesu učení a kreativitě.

Rizikovost nadužívání běžných otázek • Nepromyšlené a přílišné kladení běžných otázek je z pohledu celoživotního učení vysoce rizikové, protože dítě, žák či student získá pocit, že všechno je již objeveno, všechno je pojmenováno, všechny informace lze najít v encyklopediích či wikipediích a že jeho vlastní bádání nemá smysl. • To vede k demotivaci a ztrátě sebevědomí.

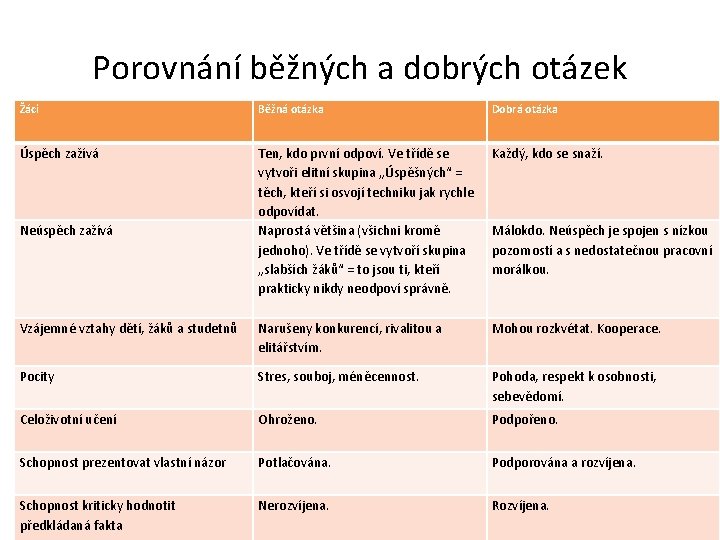
Porovnání běžných a dobrých otázek Žáci Běžná otázka Dobrá otázka Úspěch zažívá Ten, kdo první odpoví. Ve třídě se vytvoři elitní skupina „Úspěšných“ = těch, kteří si osvojí techniku jak rychle odpovídat. Naprostá většina (všichni kromě jednoho). Ve třídě se vytvoří skupina „slabších žáků“ = to jsou ti, kteří prakticky nikdy neodpoví správně. Každý, kdo se snaží. Vzájemné vztahy dětí, žáků a studetnů Narušeny konkurencí, rivalitou a elitářstvím. Mohou rozkvétat. Kooperace. Pocity Stres, souboj, méněcennost. Pohoda, respekt k osobnosti, sebevědomí. Celoživotní učení Ohroženo. Podpořeno. Schopnost prezentovat vlastní názor Potlačována. Podporována a rozvíjena. Schopnost kriticky hodnotit předkládaná fakta Nerozvíjena. Rozvíjena. Neúspěch zažívá Málokdo. Neúspěch je spojen s nízkou pozorností a s nedostatečnou pracovní morálkou.

Literatura • Jančařík, A. , Jančaříková, K. Novotná, J. “Good” Questions in Teaching. In Procedia – Social and Behavioral Sciences. V tisku. • Holt, J. (1994). Proč děti neprospívají. Praha: Agentura Strom. ISBN 80 -901662 -4 -5. • Holt, J. (1995). Jak se děti učí. Praha: Agentura Strom. • Sullivan, P. , Clarke, D. (1990). Communications in the Classroom, Geelong: Deakin University Press. • Sullivan, P. , Lilburn, P. (2010). Activités ouvertes en mathématiques. Montréal: Chanelière Education.