Do Now Special Products of Binomials You will

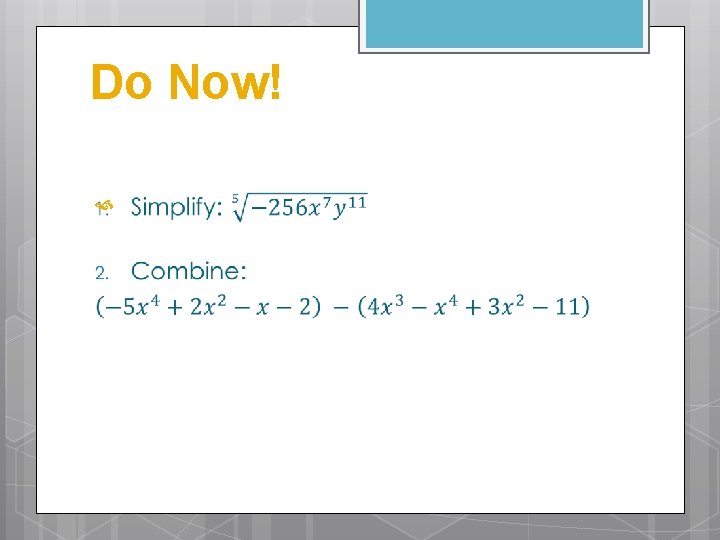
Do Now!

Special Products of Binomials You will be able to apply special products when multiplying binomials.

Being able to use these formulas will help you find products quickly. If you do not remember the formulas, you can always multiply using the distributive property, FOIL, or the box method.

Multiply: (x + 4)2 You can multiply this by rewriting this as (x + 4) OR You can use the following rule as a shortcut: (a + b)2 = a 2 + 2 ab + b 2 Lets examine both methods.

Multiply (x + 4) First terms: x 2 Outer terms: +4 x Inner terms: +4 x Last terms: +16 Notice you have two of the same answer? x x +4 x 2 +4 x Combine like terms. x 2 +8 x + 16 Let’s use the shortcut! +4 +4 x +16

Multiply: (x + 4)2 That’s why the 2 is in the formula! using (a + b)2 = a 2 + 2 ab + b 2 a is the first term, b is the second term (x + 4)2 a = x and b = 4 Plug into the formula a 2 + 2 ab + b 2 (x)2 + 2(x)(4) + (4)2 Simplify. This is the x 2 + 8 x+ 16 same answer!

Multiply: (3 x + 2 2 y) using (a + b)2 = a 2 + 2 ab + b 2 (3 x + 2 y)2 a = 3 x and b = 2 y Plug into the formula a 2 + 2 ab + b 2 (3 x)2 + 2(3 x)(2 y) + (2 y)2 Simplify 9 x 2 + 12 xy +4 y 2

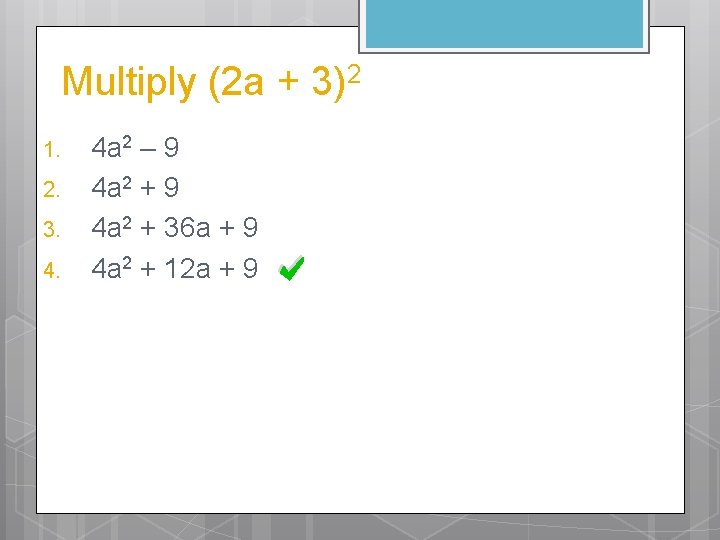
Multiply (2 a + 3)2 1. 2. 3. 4. 4 a 2 – 9 4 a 2 + 36 a + 9 4 a 2 + 12 a + 9

Multiply: (x – 5)2 using (a – b)2 = a 2 – 2 ab + b 2 Everything is the same except the signs! (x)2 – 2(x)(5) + (5)2 x 2 – 10 x + 25 Multiply: (4 x – y)2 (4 x)2 – 2(4 x)(y) + (y)2 16 x 2 – 8 xy + y 2

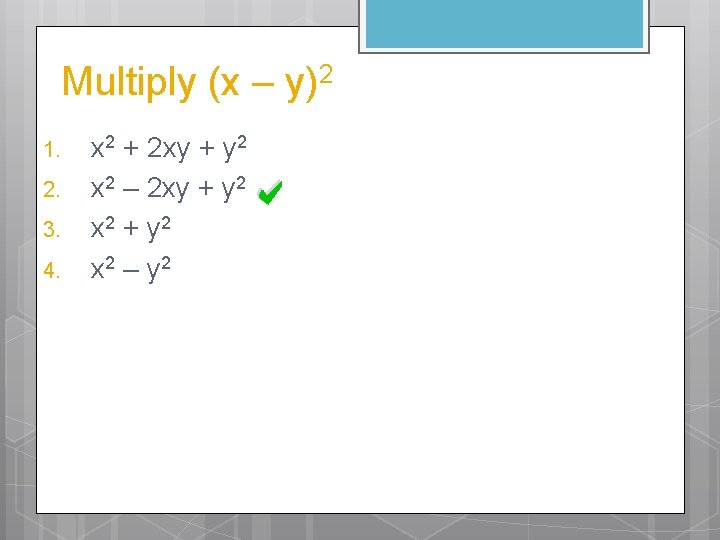
Multiply (x – y)2 1. 2. 3. 4. x 2 + 2 xy + y 2 x 2 – y 2

x x 2 +4 x +4 x 3 4 x 2 2 x +2 This is called the cube of a binomial. 8 x 8

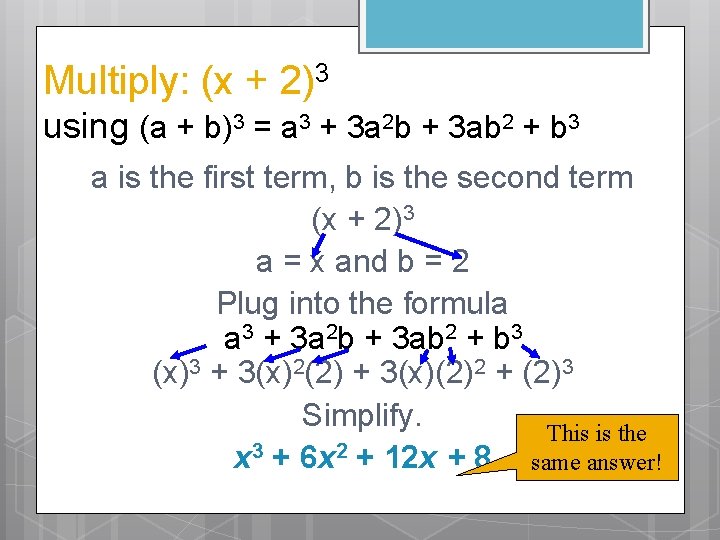
Multiply: (x + 2)3 using (a + b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 a is the first term, b is the second term (x + 2)3 a = x and b = 2 Plug into the formula a 3 + 3 a 2 b + 3 ab 2 + b 3 (x)3 + 3(x)2(2) + 3(x)(2)2 + (2)3 Simplify. This is the x 3 + 6 x 2 + 12 x + 8 same answer!

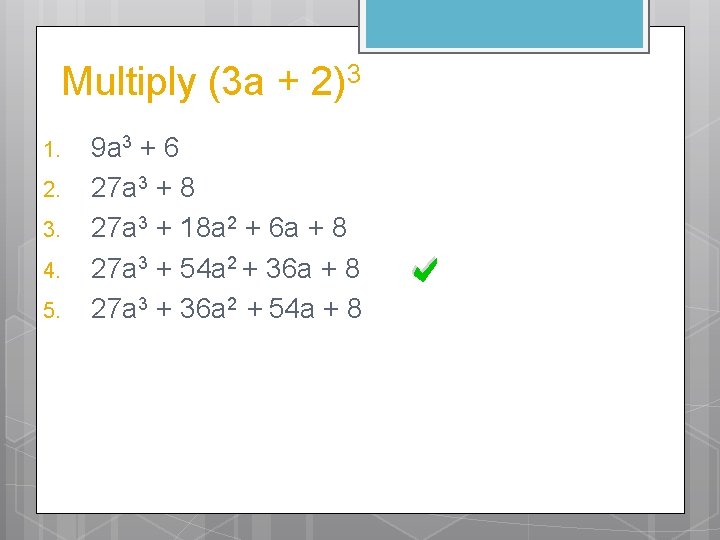
Multiply (3 a + 2)3 1. 2. 3. 4. 5. 9 a 3 + 6 27 a 3 + 8 27 a 3 + 18 a 2 + 6 a + 8 27 a 3 + 54 a 2 + 36 a + 8 27 a 3 + 36 a 2 + 54 a + 8

Multiply: (x – 1)3 using (a – b)3 = a 3 – 3 a 2 b + 3 ab 2 – b 3 Everything is the same except the signs! (x)3 – 3(x)2(1) + 3(x)(1)2 – (1)3 x 3 – 3 x 2 + 3 x – 1 Multiply: (x – 2 y)3 (x)3 – 3(x)2(2 y) + 3(x)(2 y)2 – (2 y)3 x 3 – 6 x 2 y + 12 xy 2 – 8 y 3

Multiply (x – 3)(x + 3) First terms: x 2 Outer terms: +3 x Inner terms: -3 x Last terms: -9 Notice the middle terms eliminate each other! x -3 x 2 -3 x +3 +3 x -9 x Combine like terms. x 2 – 9 This is called the difference of squares.

Multiply (x – 3)(x + 3) using (a – b)(a + b) = a 2 – b 2 You can only use this rule when the binomials are conjugates. (x – 3)(x + 3) a = x and b = 3 (x)2 – (3)2 x 2 – 9

Multiply: (y – 2)(y + 2) (y)2 – (2)2 y 2 – 4 Multiply: (5 a + 6 b)(5 a – 6 b) (5 a)2 – (6 b)2 25 a 2 – 36 b 2

Multiply (4 m – 3 n)(4 m + 3 n) 1. 2. 3. 4. 16 m 2 – 9 n 2 16 m 2 + 9 n 2 16 m 2 – 24 mn - 9 n 2 16 m 2 + 24 mn + 9 n 2