Do Now Lesson 9 1 Area of 2

Do Now!

Lesson 9 -1 Area of 2 -D Shapes Lesson 9 -1: Area of 2 -D Shapes 2

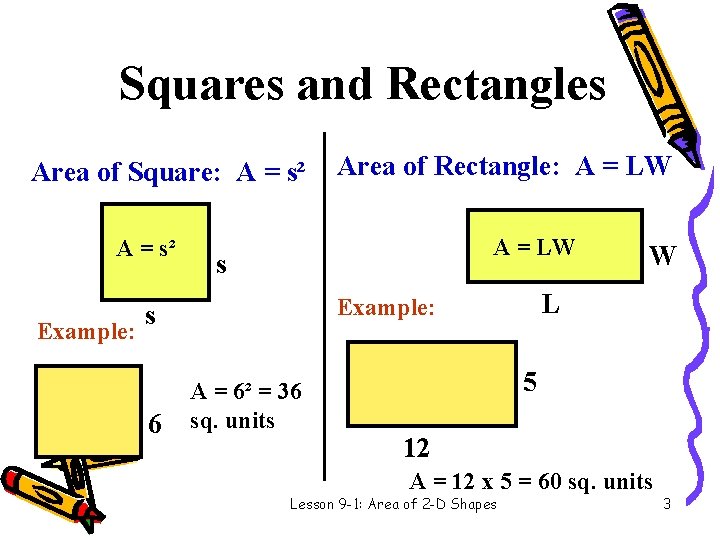
Squares and Rectangles Area of Square: A = s² Example: 6 A = LW s A = 6² = 36 sq. units W L Example: s 6 Area of Rectangle: A = LW 5 12 A = 12 x 5 = 60 sq. units Lesson 9 -1: Area of 2 -D Shapes 3

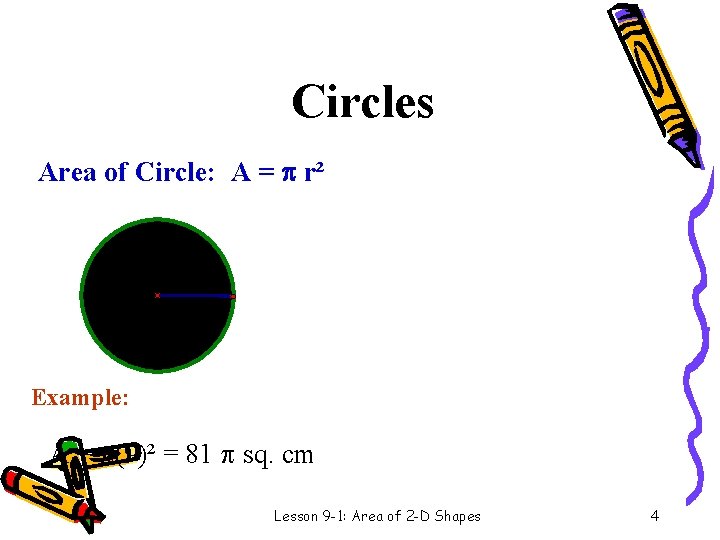
Circles Area of Circle: A = r² 9 cm r Example: A = (9)² = 81 sq. cm Lesson 9 -1: Area of 2 -D Shapes 4

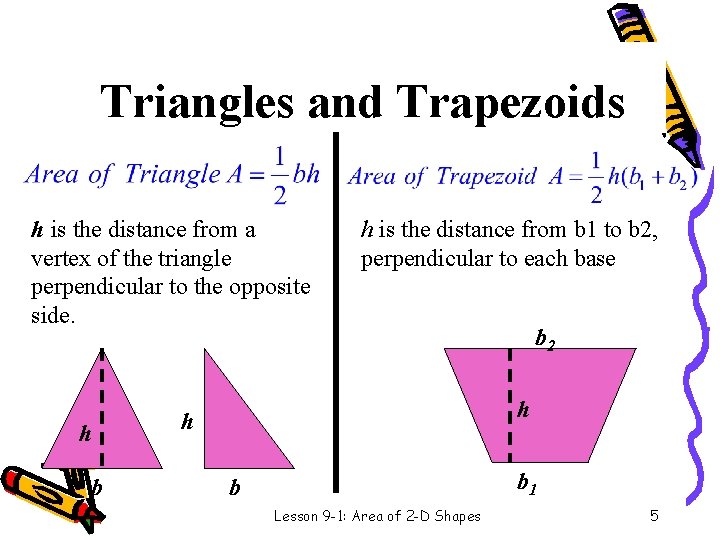
Triangles and Trapezoids h is the distance from a vertex of the triangle perpendicular to the opposite side. h b h is the distance from b 1 to b 2, perpendicular to each base b 2 h h b 1 b Lesson 9 -1: Area of 2 -D Shapes 5

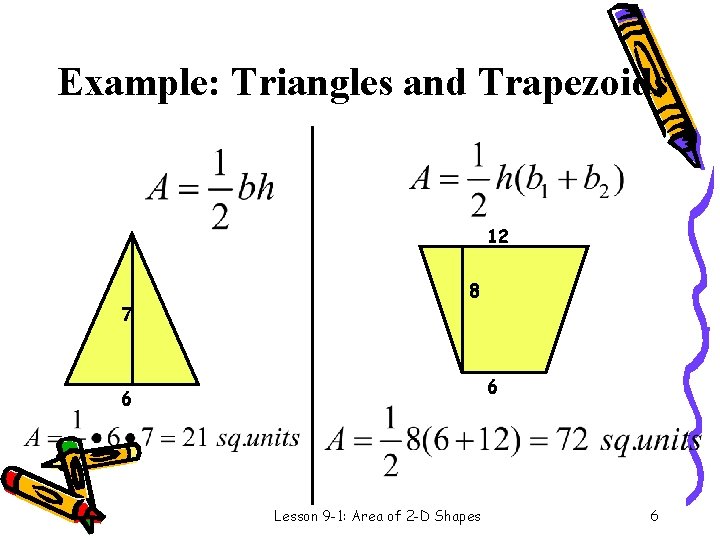
Example: Triangles and Trapezoids 12 7 8 6 6 Lesson 9 -1: Area of 2 -D Shapes 6

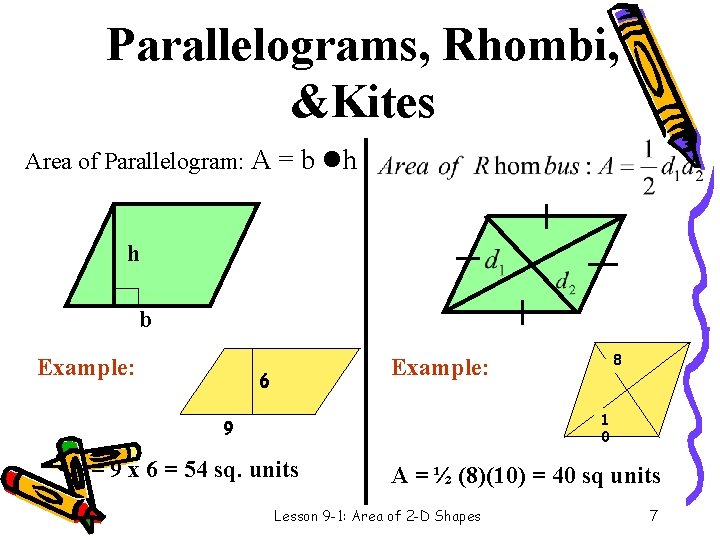
Parallelograms, Rhombi, &Kites Area of Parallelogram: A = b h h b Example: 8 Example: 6 1 0 9 A = 9 x 6 = 54 sq. units A = ½ (8)(10) = 40 sq units Lesson 9 -1: Area of 2 -D Shapes 7

VOLUME OF SOLIDS By: SAMUEL M. GIER

THINK OF THIS… Imagine transferring a 12 -ounce soft • Will the volume change? drink from • If the ice plastic is the bottle to twisted a little, will the volume change? an ice plastic container.

VOLUME OF SOLIDS DEFINITION: -is the amount of space enclosed in a solid figure. The volume of a solid is the number of cubic units contained in the solid.

VOLUME OF SOLIDS In finding volume of solids, you have to consider the area of a base and height of the solid. If the base is triangular, you have to make use of the area of a triangle, if rectangular, make use of the area of a rectangle and so on.

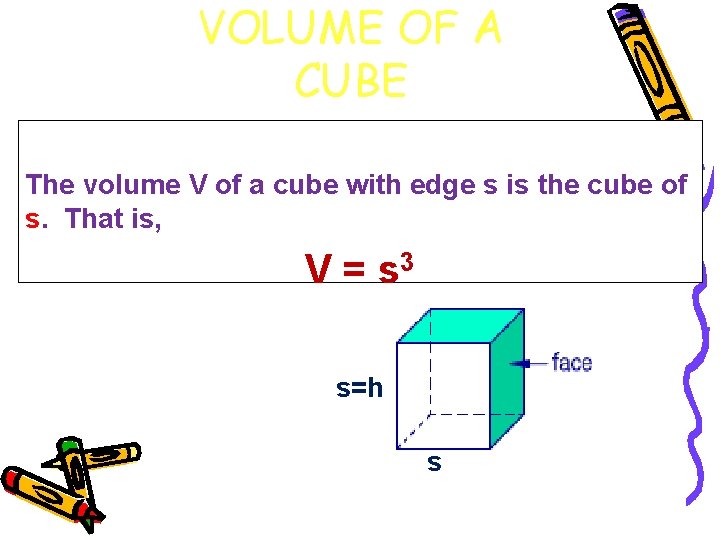
VOLUME OF A CUBE The volume V of a cube with edge s is the cube of s. That is, V = s 3 s=h s

Example 1. • Find the volume of a cube whose sides 8 cm. Solution: V = s³ 8 cm = (8 cm) ³ V = 512 cm³

VOLUME OF A RECTANGULAR PRISM

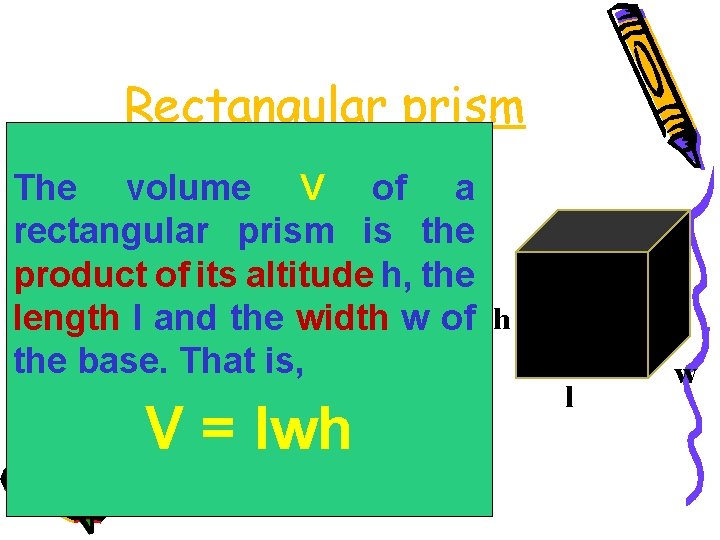
Rectangular prism The volume V of a rectangular prism is the product of its altitude h, the length l and the width w of h the base. That is, V = lwh l w

Example 2. • Find the volume of a rectangular prism. Solution: V V = lwh 5 cm 4 cm 8 cm = (8 cm)(4 cm) (5 cm) = 160 cm³

VOLUME OF A SQUARE PRISM

Square prism whose bases It is a are squares and the other faces are rectangles. Square base Height (H)

Square prism The volume V of a square prism is the product of its altitude H and the area of the base, s². That is, h s s V = s²H

Example 3. • Find the volume of a square prism. Solution: V = s²H = (4 cm) ² (5 cm) = (16 cm²) 5 cm V = 80 cm³ 5 cm 4 cm

VOLUME OF A TRIANGULAR PRISM

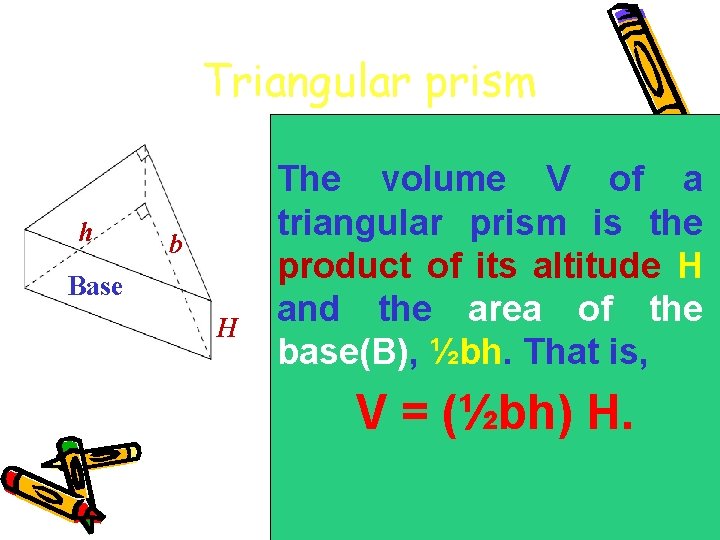
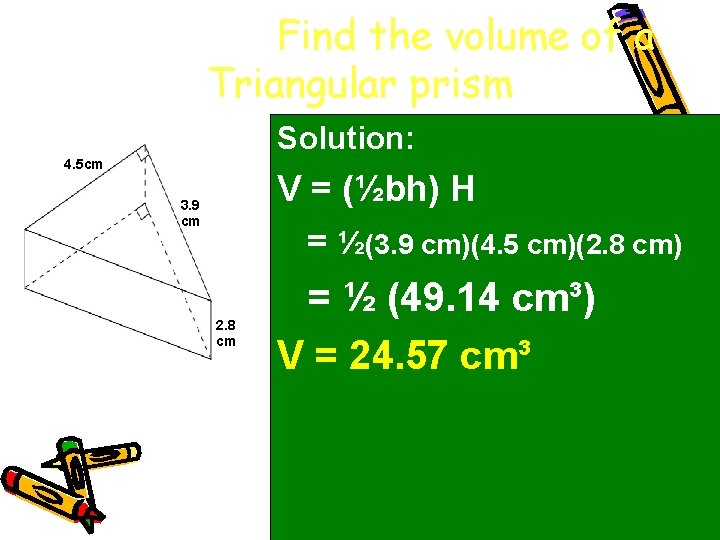
Triangular prism h b Base H The volume V of a triangular prism is the product of its altitude H and the area of the base(B), ½bh. That is, V = (½bh) H.

Example 4. Find the volume of a Triangular prism Solution: 4. 5 cm V = (½bh) H = ½(3. 9 cm)(4. 5 cm)(2. 8 cm) 3. 9 cm 2. 8 cm = ½ (49. 14 cm³) V = 24. 57 cm³

ANOTHER KIND OF POLYHEDRON PYRAMIDS

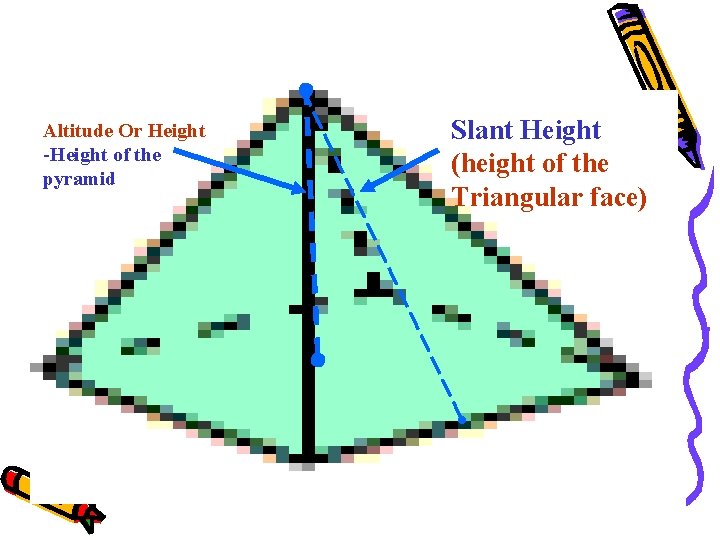
Altitude Or Height -Height of the pyramid Slant Height (height of the Triangular face)

Pyramids classified TYPES OF are PYRAMIDS 1. Square. Pyramidaccording to their the base is square. 2. Rectangular Pyramid- the base is rectangle. 3. Triangular Pyramid- the base is triangle. base.

VOLUME of PYRAMIDS • Consider a pyramid and a prism having equal altitudes and bases with equal areas. • If the pyramid is filled with water or sand its contents poured into a prism, only onethird of the prism will be filled. Thus the volume of a pyramid is w = 4 cm ⅓ the volume of the prism. h = 6 cm base l = 9 cm

Volume of pyramids The volume V of a pyramid is one third the product of its altitude h and the area B of its base. That is, V = ⅓Bh. SQUARE PYRAMID V = ⅓(s²)H RECTANGULAR PYRAMID V = ⅓(lw)H TRIANGULAR PYRAMID V = ⅓(½bh)H

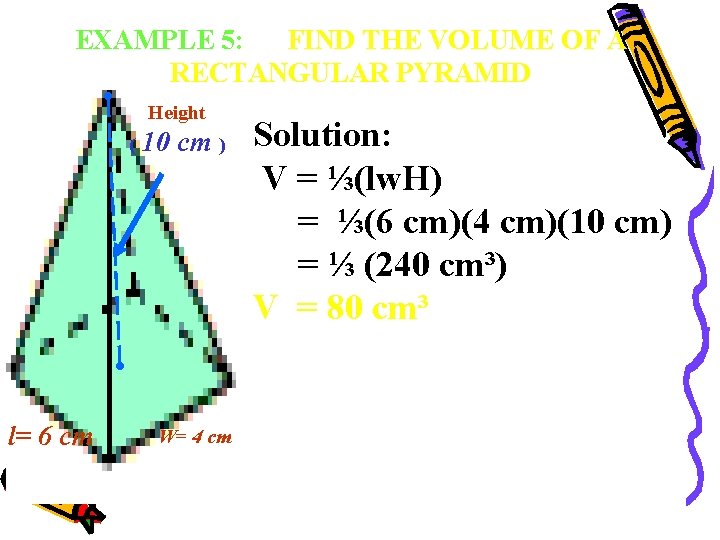
EXAMPLE 5: FIND THE VOLUME OF A RECTANGULAR PYRAMID Height ( l= 6 cm 10 cm ) W= 4 cm Solution: V = ⅓(lw. H) = ⅓(6 cm)(4 cm)(10 cm) = ⅓ (240 cm³) V = 80 cm³

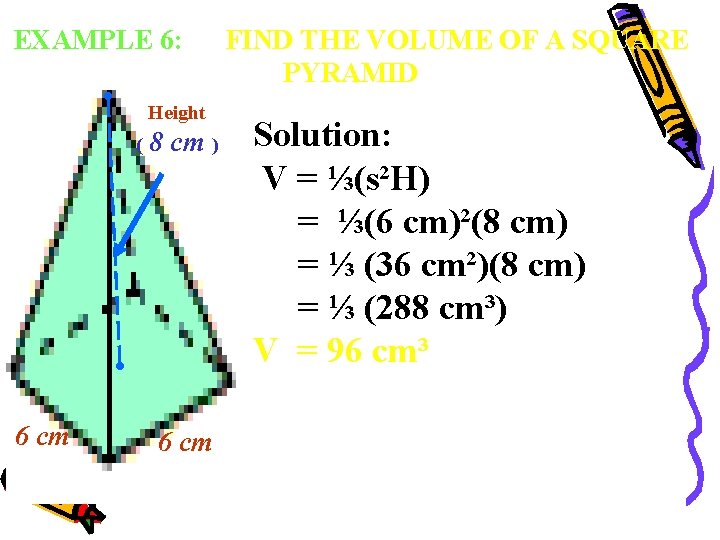
EXAMPLE 6: Height ( 6 cm 8 cm ) 6 cm FIND THE VOLUME OF A SQUARE PYRAMID Solution: V = ⅓(s²H) = ⅓(6 cm)²(8 cm) = ⅓ (36 cm²)(8 cm) = ⅓ (288 cm³) V = 96 cm³

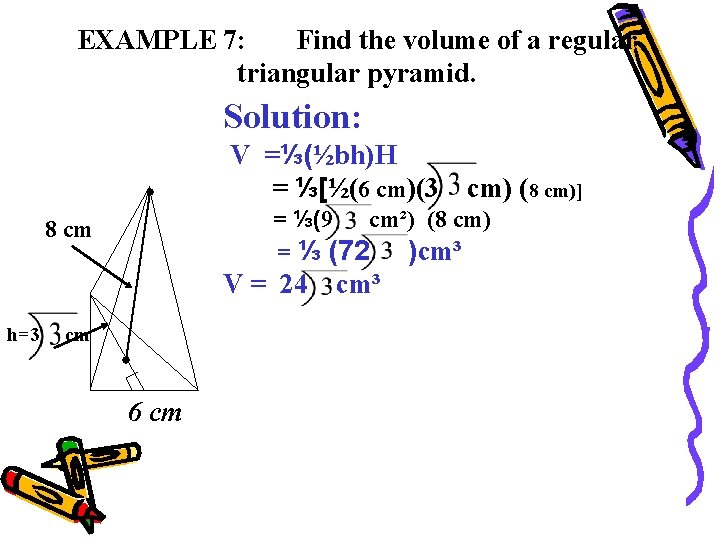
EXAMPLE 7: Find the volume of a regular triangular pyramid. Solution: V =⅓(½bh)H = ⅓[½(6 cm)(3 = ⅓(9 cm²) (8 cm) = ⅓ (72 )cm³ 8 cm V = 24 h=3 cm) (8 cm)] cm 6 cm cm³

CYLINDERS COMMON SOLIDS

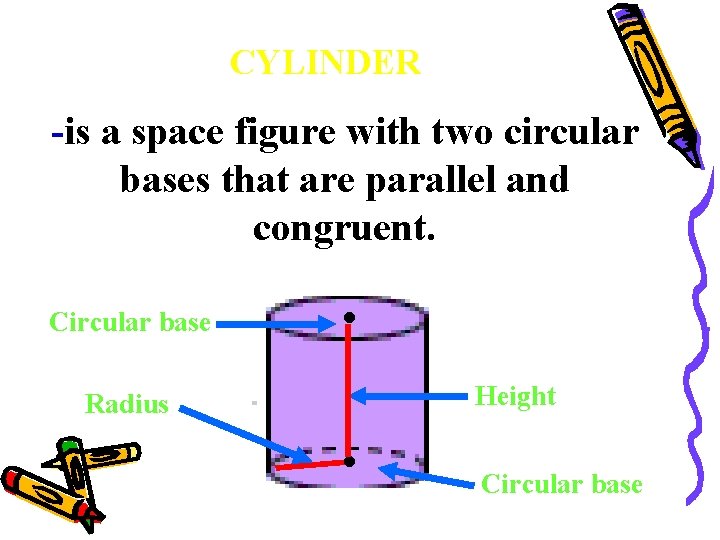
CYLINDER -is a space figure with two circular bases that are parallel and congruent. Circular base Radius . . Height Circular base

What is the CYLINDERS geometric figure represented by the bases of the cylinder? How do you compute its area?

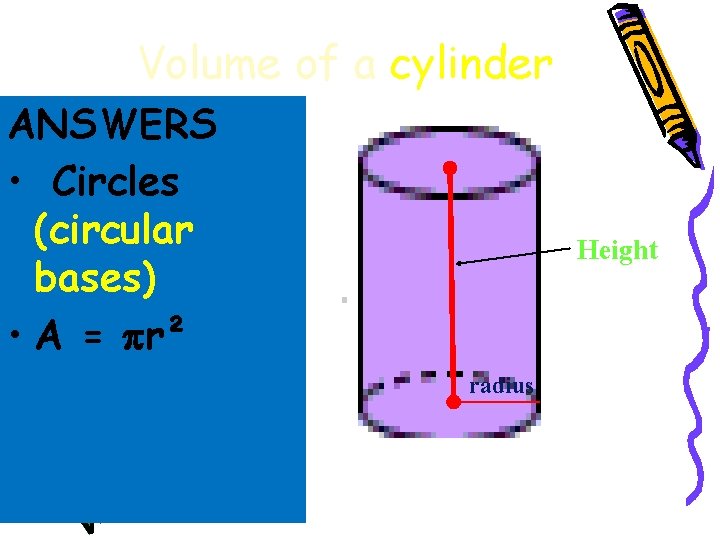
Volume of a cylinder ANSWERS • Circles (circular bases) • A = r² Height radius

Volume of a cylinder • How can the volume of a cylinder be computed? • V = Bh, where B is the area of the base and h is the height of the cylinder. • by substitution, • V= πr²h

EXAMPLE 8: Find the volume of a cylinder. Use π = 3. 14 Solution: • V = πr²h • =(3. 14)(5 cm)² 10 cm • = 3. 14( 25 cm²) (10 cm) • = 3. 14( 250 cm³) • V = 785 cm³ 10 cm 5 cm

VOLUME OF A CONE REFLECTIVE TRAFFIC CONE

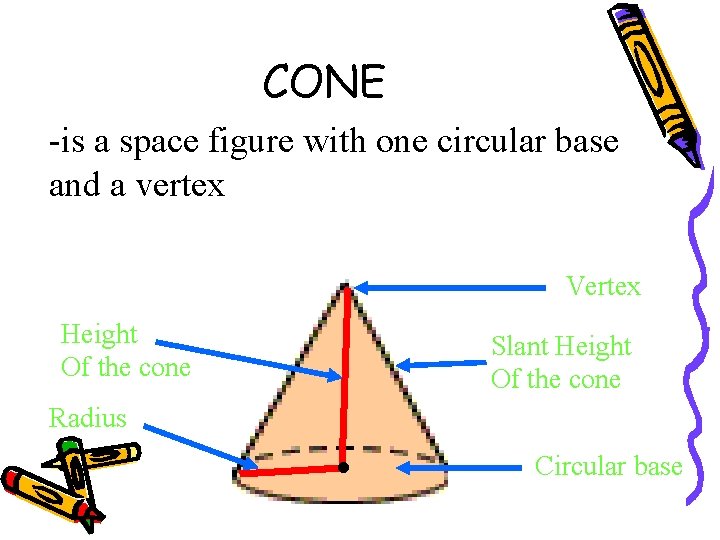
CONE -is a space figure with one circular base and a vertex Vertex Height Of the cone Radius . Slant Height Of the cone Circular base

VOLUME of a CONE • Consider a CONE and a CYLINDER having equal altitudes and bases with equal areas. • If the CONE is filled with water or sand its contents poured into a CYLIDER, only one- third of the CYLINDER will be filled. Thus the volume of a CONE is ⅓ the volume of the CYLINDER. h r

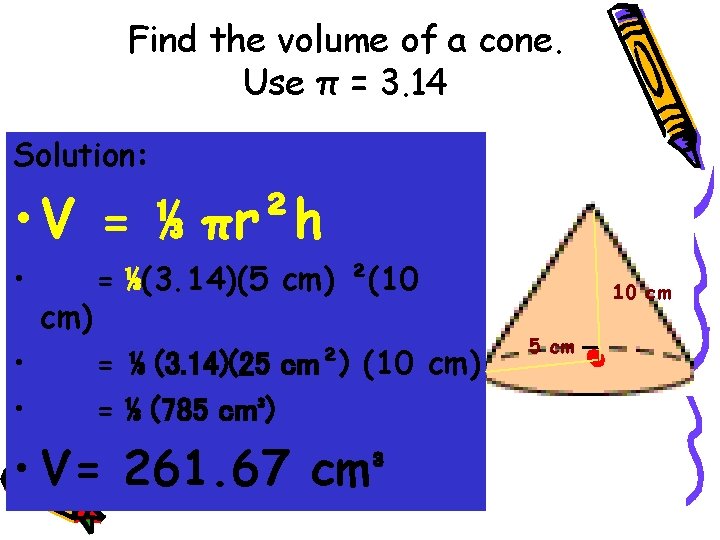
Volume of a cone • How can the volume of a cone be computed? • V = ⅓Bh, where B is the area of the base and h is the height of the cone. • by substitution, • V= ⅓ πr²h

Find the volume of a cone. Use π = 3. 14 Solution: • V = ⅓ πr²h • • • cm) = ⅓(3. 14)(5 cm) ²(10 = ⅓ (3. 14)(25 cm²) (10 cm) = ⅓ (785 cm³) • V= 261. 67 cm³ 10 cm 5 cm

Find the volume of a cone. Use π = 3. 14 Solution: • Step 1. find h. n. V = ⅓ πr²h • Using Pythagorean n = ⅓(3. 14)(3 cm) ²(4 cm) theorem, n = ⅓ (3. 14)(9 ²) (4 cm) • h²= 5² -cm 3² n = ⅓ (113. 04 cm³) • =25 -9 n V= • h² 37. 68 = 16 • h = 4 cm cm³ 5 cm 4 cm 3 cm

VOLUME OF A SPHERE THE EARTH BALLS

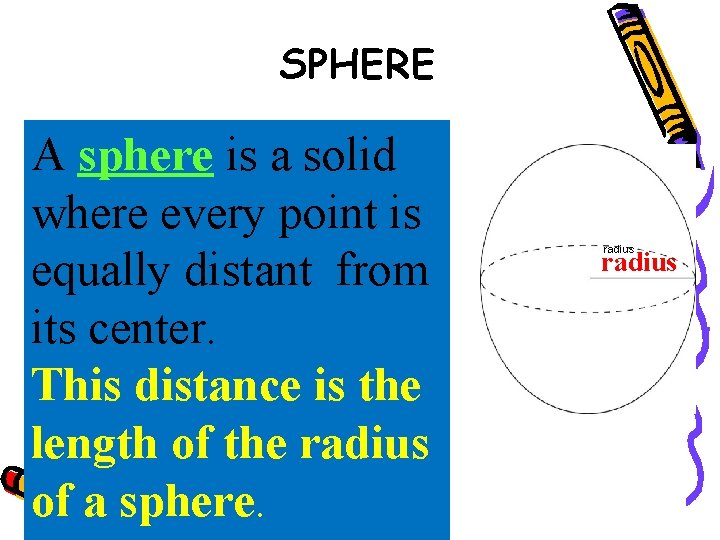
SPHERE A sphere is a solid where every point is equally distant from its center. This distance is the length of the radius of a sphere. radius

VOLUME OF A SPHERE BALL The formula to find the VOLUMEof a sphere is V = πr³, where r is the length of its radius. How can the volume of a sphere be computed?

Archimedes of Syracuse (287 -212 BC) • is regarded as the greatest of Greek mathematicians, and was also an inventor of many mechanical devices (including the screw, the pulley, and the lever). • He perfected integration using Eudoxus' method of exhaustion, and found the areas and volumes of many

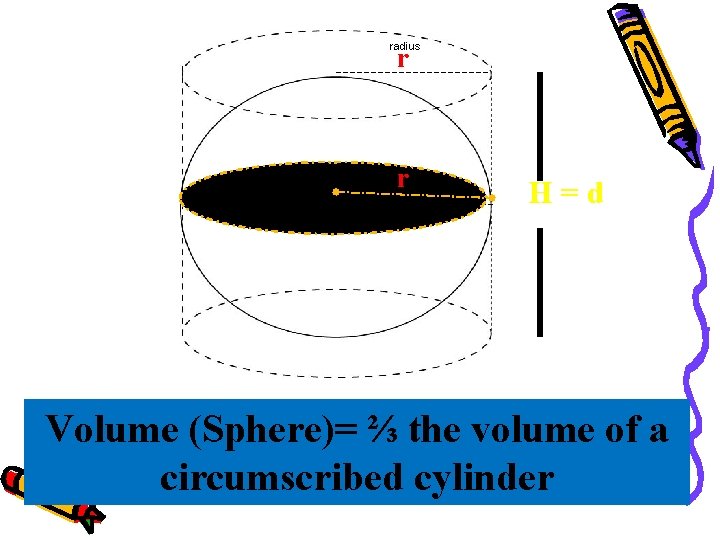
Archimedes of Syracuse (287 -212 BC) • A famous result of his is that the volume of a sphere is two-thirds the volume of its circumscribed cylinder, a picture of which was inscribed on his tomb.

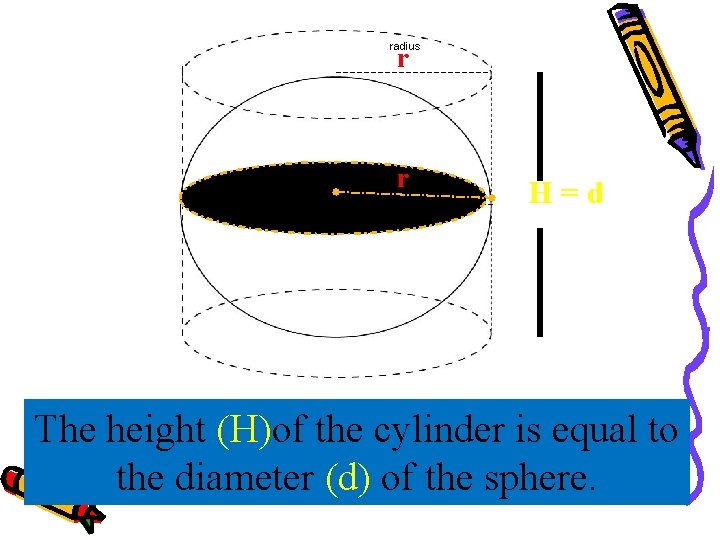
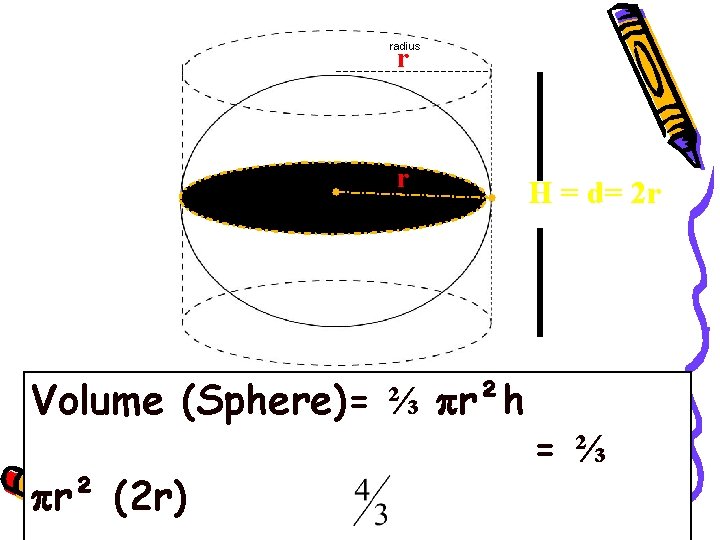
radius r r radius H=d The height (H)of the cylinder is equal to the diameter (d) of the sphere.

radius r r radius H=d Volume (Sphere)= ⅔ the volume of a circumscribed cylinder

radius r r radius Volume (Sphere)= ⅔ r²h r² (2 r) H = d= 2 r = ⅔

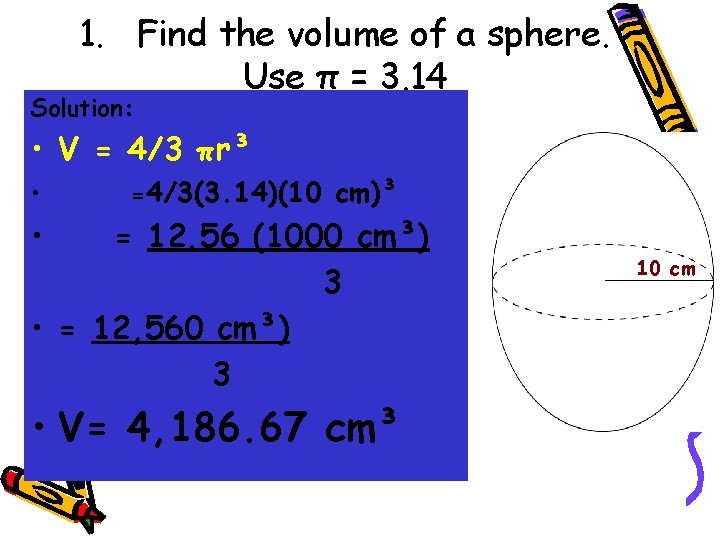
1. Find the volume of a sphere. Use π = 3. 14 Solution: • V = 4/3 πr³ • =4/3(3. 14)(10 cm)³ • = 12. 56 (1000 cm³) 3 • = 12, 560 cm³) 3 • V= 4, 186. 67 cm³ 10 cm

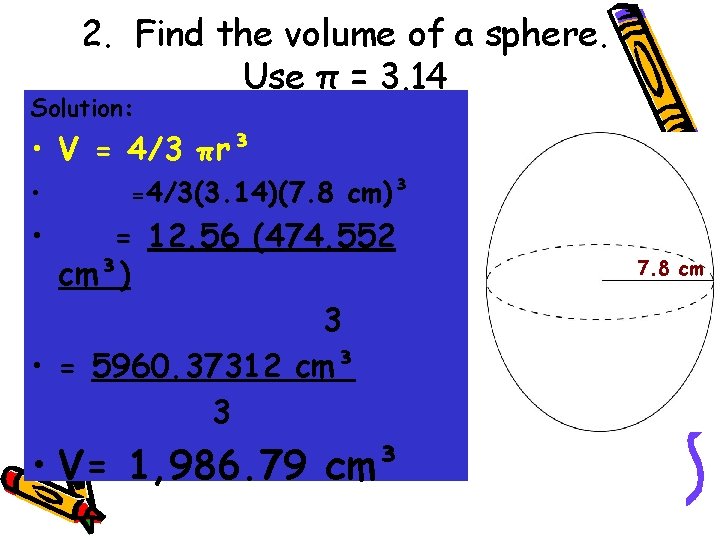
2. Find the volume of a sphere. Use π = 3. 14 Solution: • V = 4/3 πr³ • =4/3(3. 14)(7. 8 cm)³ • = 12. 56 (474. 552 cm³) 3 • = 5960. 37312 cm³ 3 • V= 1, 986. 79 cm³ 7. 8 cm