Do Now A spring has a length of

Oscillations and Waves Review Be sure to review the voter questions that we previously

A. B. C. D. 1. An SHO goes through 8 cycles in 4 seconds.

A. B. C. D. E. 2. An SHO goes through 8 cycles in 4

3. A mass on a spring oscillates SHM. At which location shown is in

4. A mass on a spring oscillates SHM. At which location shown is in

5. A pulse is sent along a string The is attached to a second,

5. A pulse is sent along a string is attached to a second, thicker

5. Concep. Test 11. 1 a. Harmonic Motion I A mass on a spring

6. A pendulum oscillates in SHM. At which location shown is the kinetic energy

7. Concep. Test 11. 1 b. Harmonic Motion II A mass on a spring

8. Period of a Spring I A glider with a spring attached to each

9. Period of a Spring Ia A glider with a spring attached to each

10. Spring on the Moon A mass oscillates on a vertical spring with period

11. Period of a Pendulum I Two pendula have the same length, but different

12. Period of a Pendulum I Two pendula have the same length and same

13. Damped Pendulum After a pendulum starts swinging, its amplitude gradually decreases with time

14. Swinging in the Rain You are sitting on a swing. A friend gives

15. Sound It Out Does a longitudinal wave, 1) yes such as a sound

16. The Wave At a football game, the “wave” might circulate through the stands

17. Wave Motion I 1) Consider a wave on a string moving to the

18. Wave Motion Ia 1) Consider a wave on a string moving to the

19. Wave Motion II 1) Consider a wave on a string moving to the

20. Wave Motion IIa 1) Consider a wave on a string moving to the

21. Out to Sea A boat is moored in a fixed location, and 1)

21. Out to Sea 1) 1 second A boat is moored in a fixed

22. Out to Sea A boat is moored in a fixed location, and 1)

23. A pulse approaches a fixed end as shown. When it returns the pulse

24. A pulse approaches an open end as shown. When it returns the pulse

25. Two pulses are moving to the right. The one closest to the wall

26. The amplitude of the wave below is A. B. C. D. E. 0

27. The wavelength of the wave below is A. B. C. D. E. 0

28. The wave below has a frequency of 10 Hz. Its speed is A.

29. The wave below has a frequency of 10 Hz. Its period is A.

30. A standing wave is shown below. When the string at position a is

31. Standing Waves I A string is clamped at both ends and plucked so

32. Standing Waves II A string is clamped at both ends and plucked so

33. Concep. Test 11. 1 c. Harmonic Motion III A mass on a spring

34. Concep. Test 11. 8 b. Period of a Pendulum II Two pendula have

Slides: 72

Download presentation

Do Now A spring has a length of 3 m. It has a mass of 20 kg and a spring constant of 5 N/m. The spring is pulled 1 m from its equilibrium position and then released. What is the period of oscillation? m 20 6. 28 4 12. 6 s T 2 k 5

Oscillations and Waves Review Be sure to review the voter questions that we previously went over in class. (The material on the mathematics of sines and cosines will not be covered. )

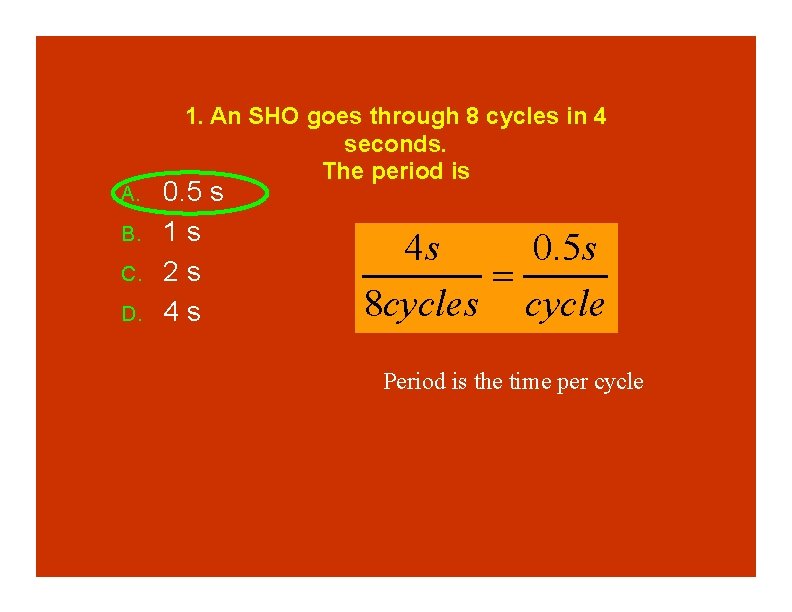
A. B. C. D. 1. An SHO goes through 8 cycles in 4 seconds. The period is 0. 5 s 1 s 2 s 4 s

A. B. C. D. 1. An SHO goes through 8 cycles in 4 seconds. The period is 0. 5 s 1 s 2 s 4 s 4 s 0. 5 s 8 cycles cycle Period is the time per cycle

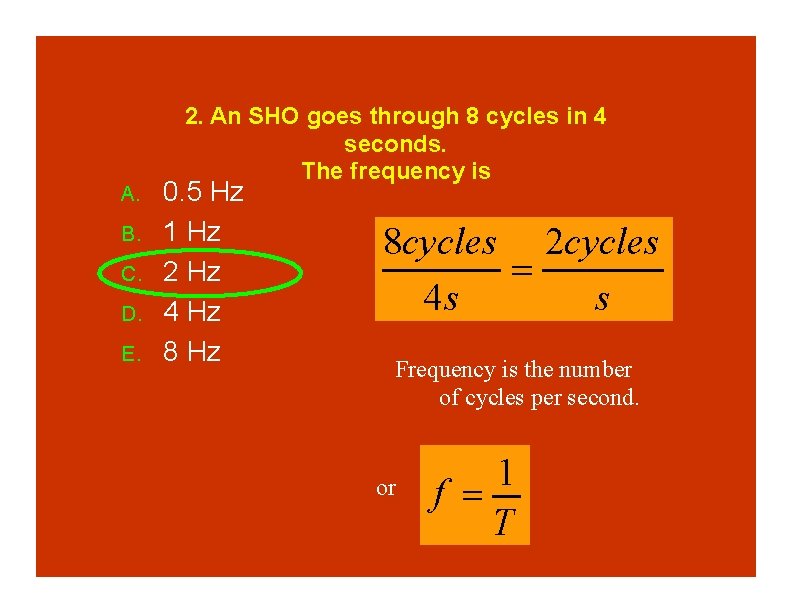
A. B. C. D. E. 2. An SHO goes through 8 cycles in 4 seconds. The frequency is 0. 5 Hz 1 Hz 2 Hz 4 Hz 8 Hz

A. B. C. D. E. 2. An SHO goes through 8 cycles in 4 seconds. The frequency is 0. 5 Hz 1 Hz 2 Hz 4 Hz 8 cycles 2 cycles 4 s s Frequency is the number of cycles per second. or 1 f T

3. A mass on a spring oscillates SHM. At which location shown is in the velocity the greatest magnitude? A. B. C. D. x=-A x=0 x=B x=+A B

3. A mass on a spring oscillates SHM. At which location shown is in the velocity the greatest magnitude? A. B. C. D. x=-A x=0 x=B x=+A In SHM, velocity is maximum at the center. B

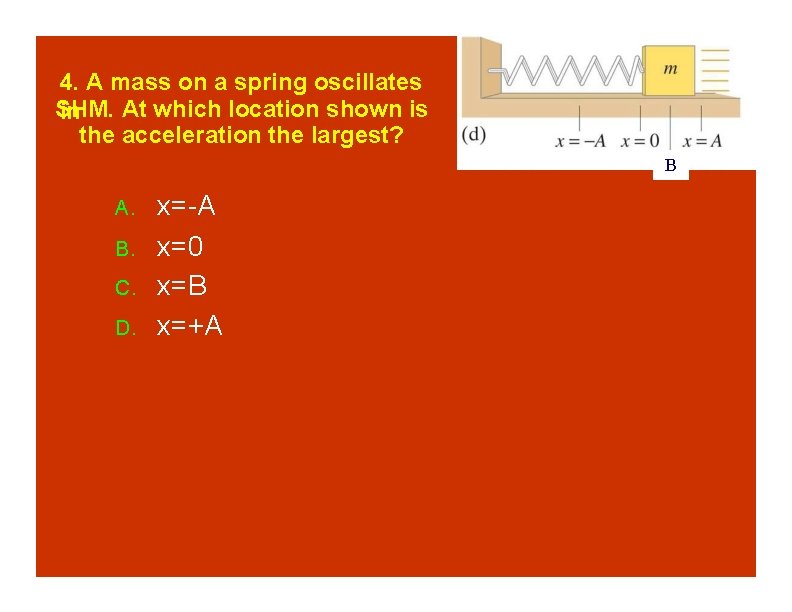
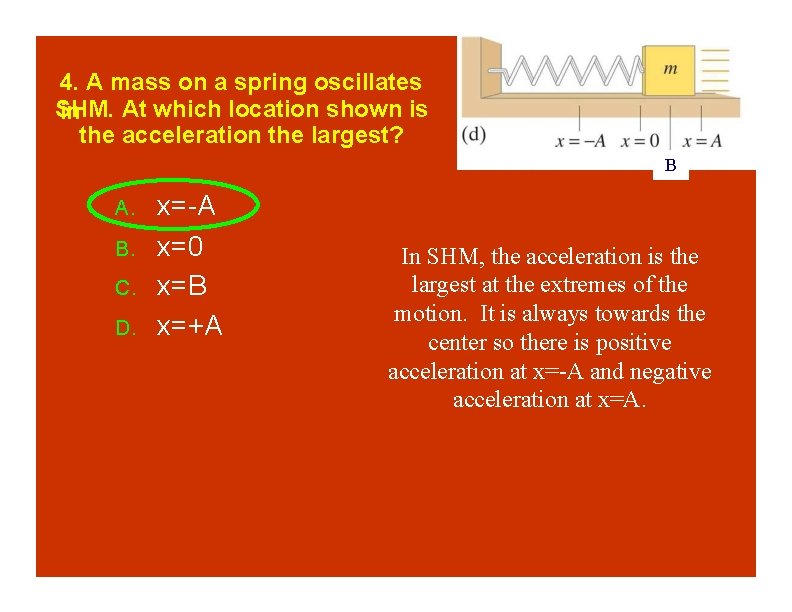
4. A mass on a spring oscillates SHM. At which location shown is in the acceleration the largest? B A. B. C. D. x=-A x=0 x=B x=+A

4. A mass on a spring oscillates SHM. At which location shown is in the acceleration the largest? B A. B. C. D. x=-A x=0 x=B x=+A In SHM, the acceleration is the largest at the extremes of the motion. It is always towards the center so there is positive acceleration at x=-A and negative acceleration at x=A.

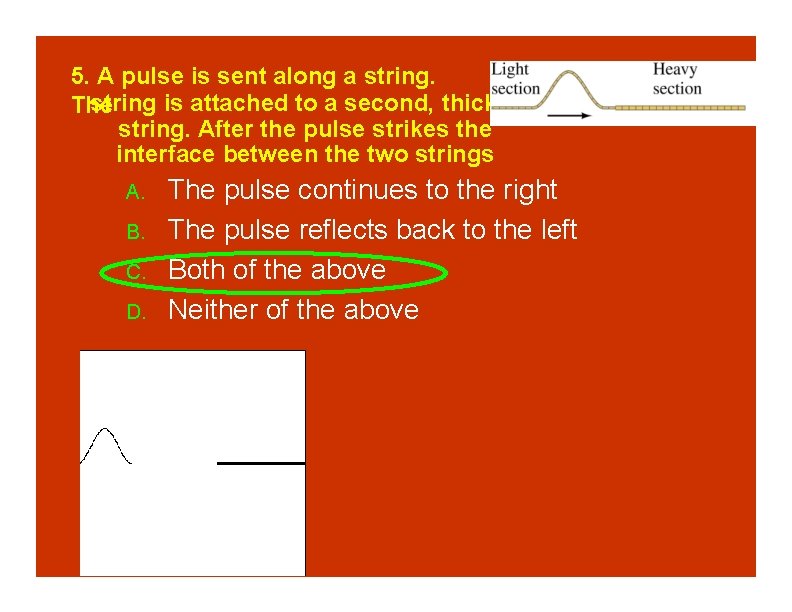
5. A pulse is sent along a string The is attached to a second, thicker string. After the pulse strikes the interface between the two strings A. B. C. D. The pulse continues to the right The pulse reflects back to the left Both of the above Neither of the above

5. A pulse is sent along a string is attached to a second, thicker The string. After the pulse strikes the interface between the two strings A. B. C. D. The pulse continues to the right The pulse reflects back to the left Both of the above Neither of the above

5. Concep. Test 11. 1 a. Harmonic Motion I A mass on a spring in SHM has amplitude A and period T. What is the total distance traveled by the mass after a time interval T? 1) 0 2) A/2 3) A 4) 2 A 5) 4 A In the time interval T (the period), the mass goes through one complete oscillation back to the starting point. The distance it covers is: A + A + A (4 A).

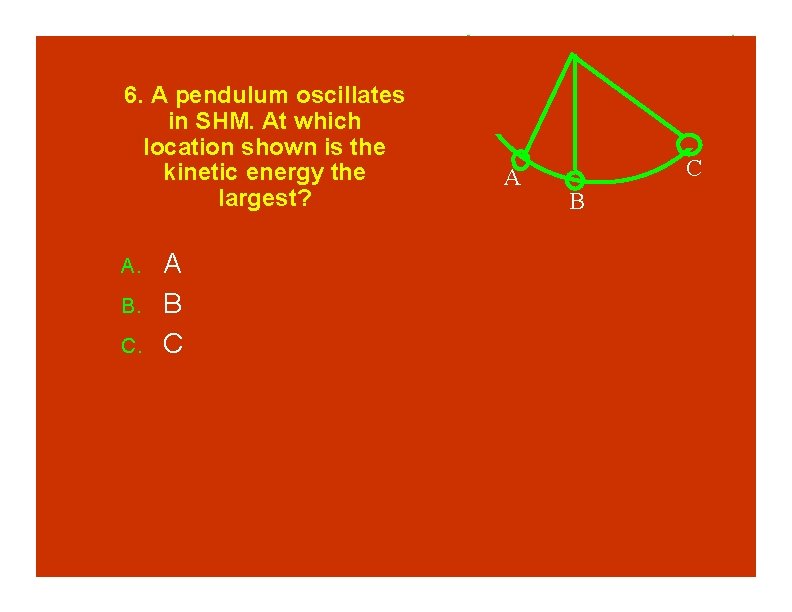
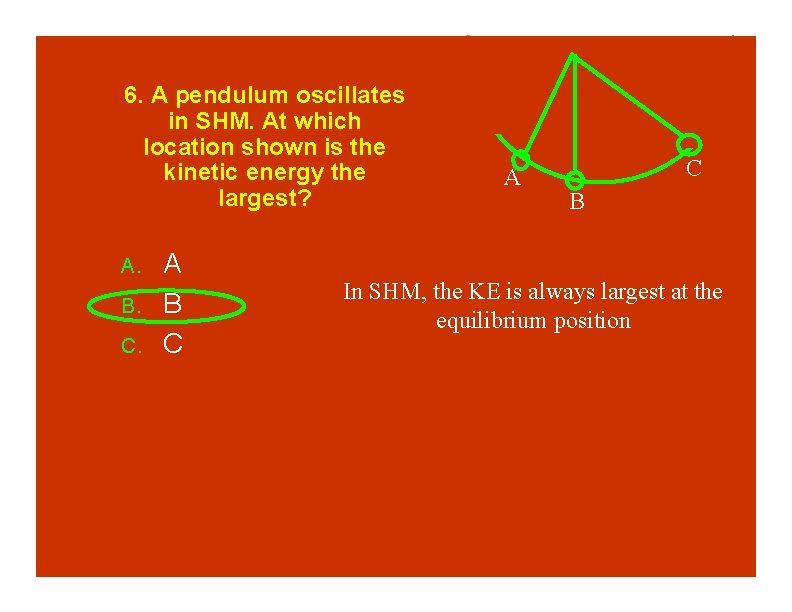
6. A pendulum oscillates in SHM. At which location shown is the kinetic energy the largest? A. B. C. A B C A C B

6. A pendulum oscillates in SHM. At which location shown is the kinetic energy the largest? A. B. C. A B C A C B In SHM, the KE is always largest at the equilibrium position

7. Concep. Test 11. 1 b. Harmonic Motion II A mass on a spring in SHM has amplitude A and period T. What is the net displacement of the mass after a time interval T? 1) 0 2) A/2 3) A 4) 2 A 5) 4 A

7. Concep. Test 11. 1 b. Harmonic Motion II A mass on a spring in SHM has amplitude A and period T. What is the net displacement of the mass after a time interval T? 1) 0 2) A/2 3) A 4) 2 A 5) 4 A The displacement is x = x 2–x 1. Since the initial and final positions of the mass are the same (it ends up back at its original position), then the displacement is zero. Follow-up: What is the net displacement after a half of a period?

8. Period of a Spring I A glider with a spring attached to each end oscillates with a certain period. If the mass of the glider is doubled, what will happen to the period? 1) period will increase 2) period will not change 3) period will decrease The period is proportional to the square root of the mass. So an increase in mass will lead to an increase in the period of motion. T T == 22 ((mm//kk))

9. Period of a Spring Ia A glider with a spring attached to each end oscillates with a certain period. If the amplitude of the motion is doubled, what will happen to the period? 1) period will increase 2) period will not change 3) period will decrease

10. Spring on the Moon A mass oscillates on a vertical spring with period T. If the whole setup is taken to the Moon, how does the period change? 1) period will increase 2) period will not change 3) period will decrease The period of simple harmonic motion only depends on the mass and the spring constant and does not depend on the acceleration due to gravity. By going to the Moon, the value of g has been reduced, but that does not affect the period of the oscillating mass-spring system. Follow-up: Will the period be the same on any planet?

11. Period of a Pendulum I Two pendula have the same length, but different masses attached to the string. How do their periods compare? 1) period is greater for the greater mass 2) period is the same for both cases 3) period is greater for the smaller mass The period of a pendulum depends on the length and the acceleration due to gravity, but it does not depend on the mass of the bob. T T == 22 ((LL//gg))

12. Period of a Pendulum I Two pendula have the same length and same mass, but different amplitudes. How do their periods compare? 1) period is greater for the greater mass 2) period is the same for both cases 3) period is greater for the smaller mass

13. Damped Pendulum After a pendulum starts swinging, its amplitude gradually decreases with time because of friction. 1) period increases What happens to the period of the 3) period decreases pendulum during this time? 2) period does not change

13. Damped Pendulum After a pendulum starts swinging, its amplitude gradually decreases with time because of friction. 1) period increases 2) period does not change 3) period decreases What happens to the period of the pendulum during this time? The period of a pendulum does not depend on its amplitude, but only on its length and the acceleration due to gravity. T 2 L g

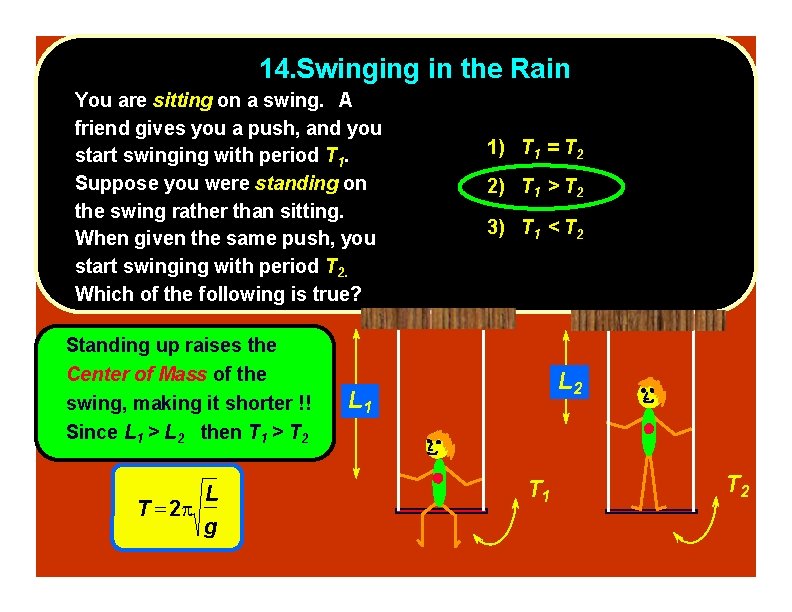
14. Swinging in the Rain You are sitting on a swing. A friend gives you a push, and you start swinging with period T 1. Suppose you were standing on the swing rather than sitting. When given the same push, you start swinging with period T 2. Which of the following is true? 1) T 1 = T 2 2) T 1 > T 2 3) T 1 < T 2 T 1

15. Sound It Out Does a longitudinal wave, 1) yes such as a sound wave, 2) no have an amplitude ? 3) it depends on the medium the wave is in air pressure high normal low A x

15. Sound It Out Does a longitudinal wave, 1) yes such as a sound wave, 2) no have an amplitude ? 3) it depends on the medium the wave is in All wave types — transverse, longitudinal, surface — have all of these properties: wavelength, frequency, amplitude, velocity, period air pressure high normal low A x

16. The Wave At a football game, the “wave” might circulate through the stands and move around the stadium. In this wave motion, people stand up and sit down as the wave passes. What type of wave would this be characterized as? 1) polarized wave 2) longitudinal wave 3) lateral wave 4) transverse wave 5) soliton wave The people are moving up and down, and the wave is traveling around the stadium. Thus, the motion of the wave is perpendicular to the oscillation direction of the people, and so this is a transverse wave. Follow-up: What type of wave occurs when you toss a pebble in a pond?

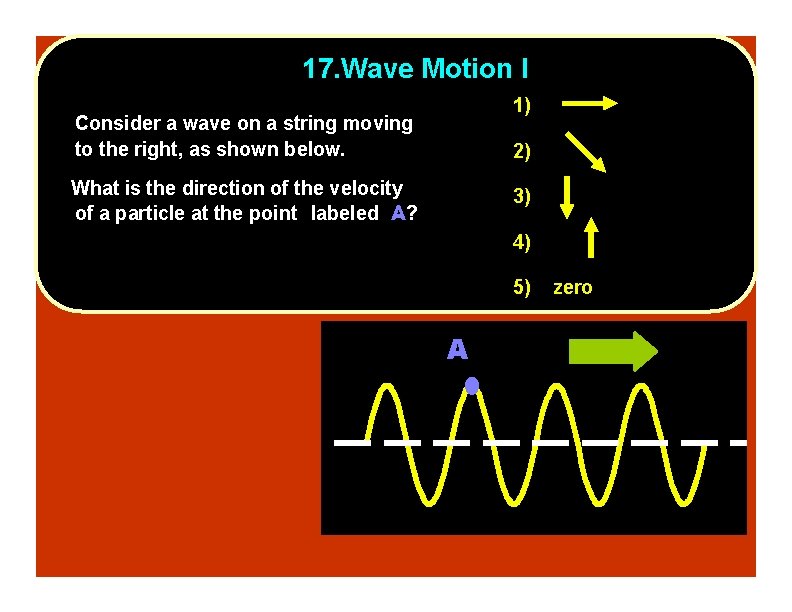
17. Wave Motion I 1) Consider a wave on a string moving to the right, as shown below. 2) What is the direction of the velocity of a particle at the point labeled A? 3) 4) 5) A zero

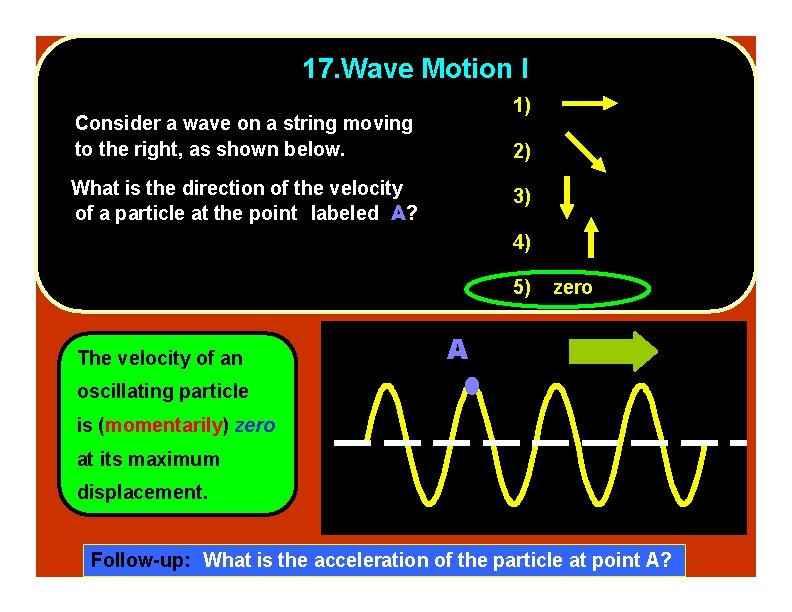
17. Wave Motion I 1) Consider a wave on a string moving to the right, as shown below. 2) What is the direction of the velocity of a particle at the point labeled A? 3) 4) 5) The velocity of an zero A oscillating particle is (momentarily) zero at its maximum displacement. Follow-up: What is the acceleration of the particle at point A?

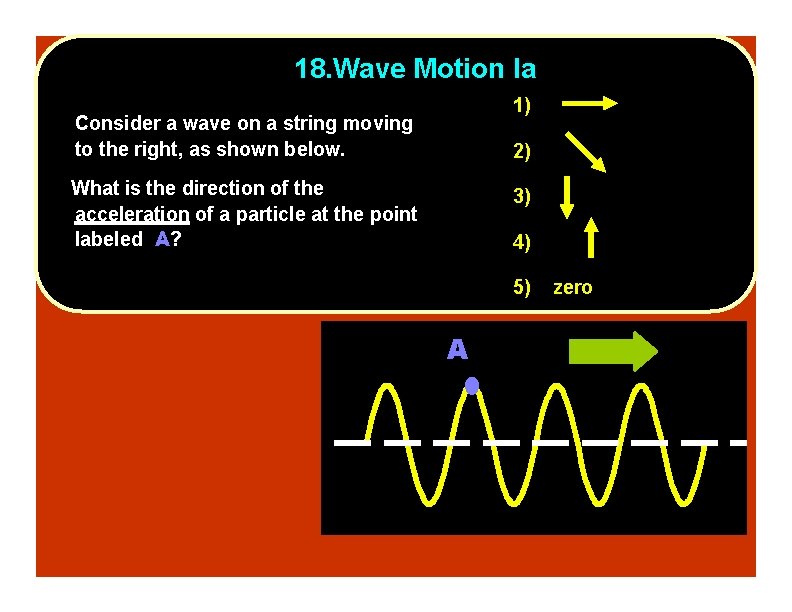
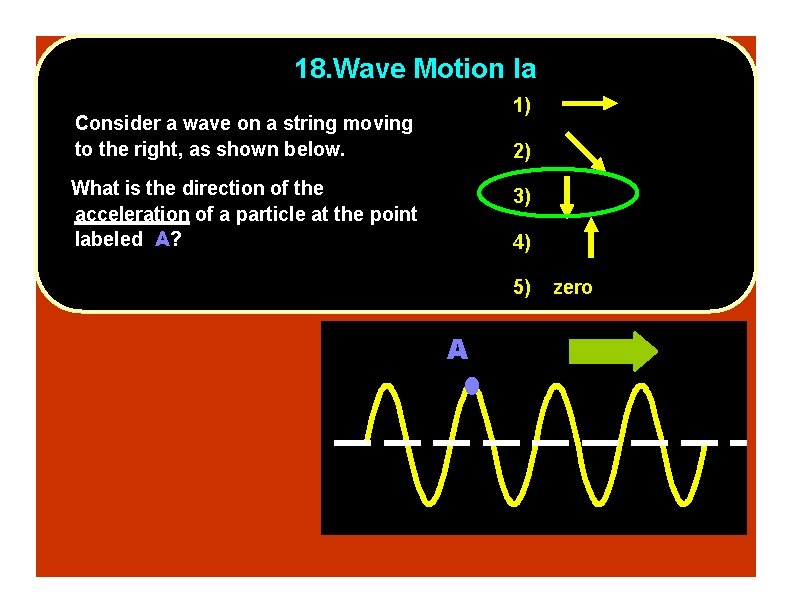
18. Wave Motion Ia 1) Consider a wave on a string moving to the right, as shown below. 2) What is the direction of the acceleration of a particle at the point labeled A? 3) 4) 5) A zero

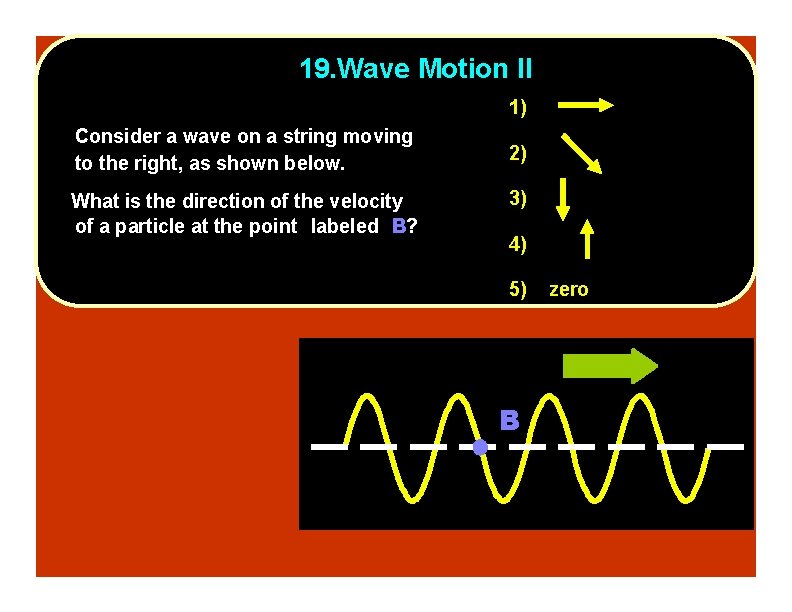
19. Wave Motion II 1) Consider a wave on a string moving to the right, as shown below. What is the direction of the velocity of a particle at the point labeled B? 2) 3) 4) 5) B zero

19. Wave Motion II 1) Consider a wave on a string moving to the right, as shown below. What is the direction of the velocity of a particle at the point labeled B? 2) 3) 4) 5) zero The wave is moving to the right, so the particle at B has to start moving upwards B in the next instant of time. Follow-up: What is the acceleration of the particle at point B?

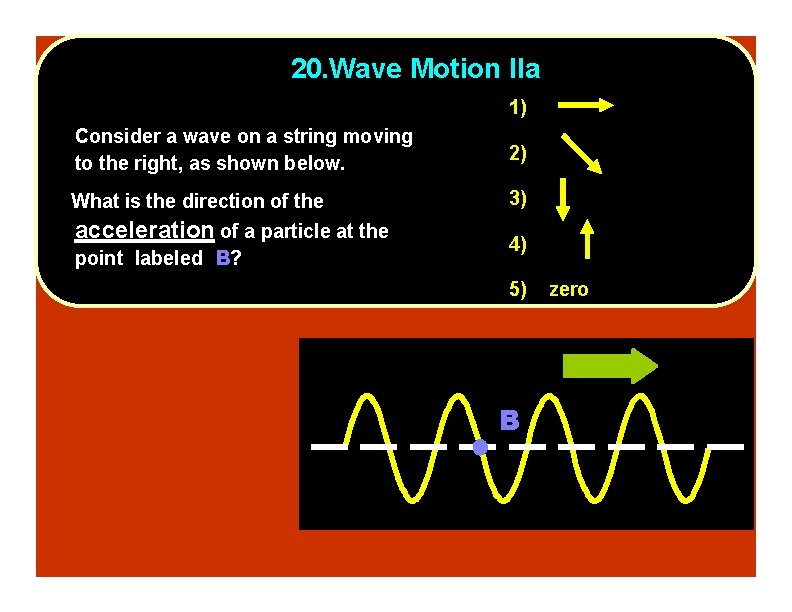
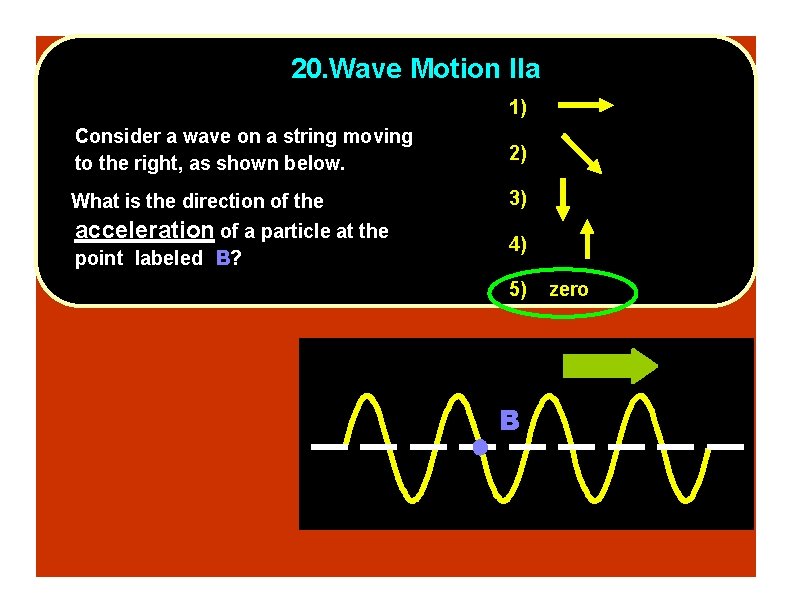
20. Wave Motion IIa 1) Consider a wave on a string moving to the right, as shown below. 2) What is the direction of the 3) acceleration of a particle at the point labeled B? 4) 5) B zero

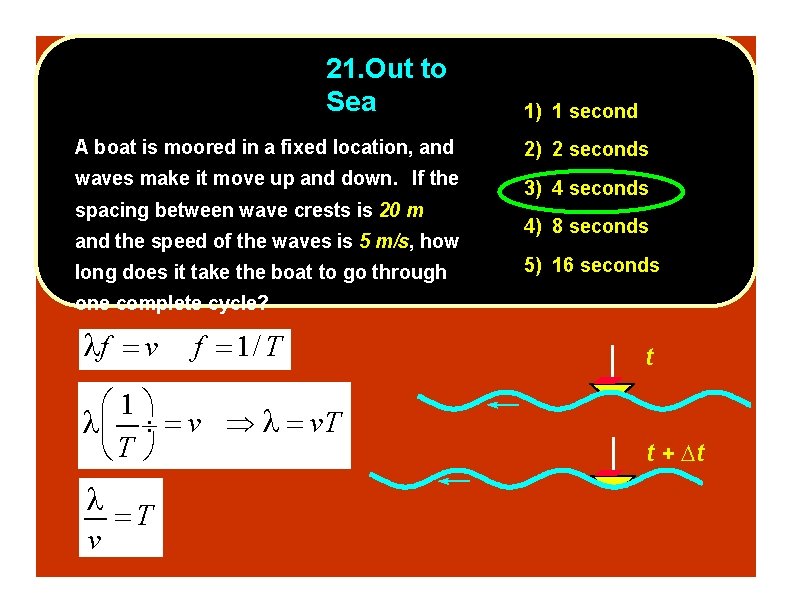
21. Out to Sea A boat is moored in a fixed location, and 1) 1 second waves make it move up and down. If the 2) 2 seconds spacing between wave crests is 20 m and the speed of the waves is 5 m/s, how long does it take the boat to go through one complete cycle? 3) 4 seconds 4) 8 seconds 5) 16 seconds t t + t

21. Out to Sea 1) 1 second A boat is moored in a fixed location, and 2) 2 seconds waves make it move up and down. If the 3) 4 seconds spacing between wave crests is 20 m and the speed of the waves is 5 m/s, how long does it take the boat to go through 4) 8 seconds 5) 16 seconds one complete cycle? f v f 1/ T 1 v v. T T T v t t + t

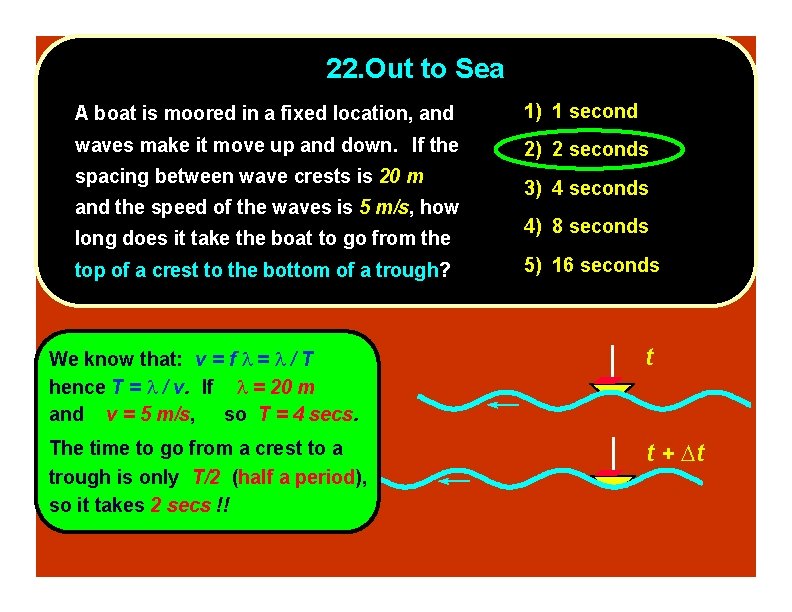
22. Out to Sea A boat is moored in a fixed location, and 1) 1 second waves make it move up and down. If the 2) 2 seconds spacing between wave crests is 20 m and the speed of the waves is 5 m/s, how long does it take the boat to go from the top of a crest to the bottom of a trough? 3) 4 seconds 4) 8 seconds 5) 16 seconds We know that: v = f = / T hence T = / v. If = 20 m and v = 5 m/s, so T = 4 secs. t The time to go from a crest to a trough is only T/2 (half a period), so it takes 2 secs !! t + t

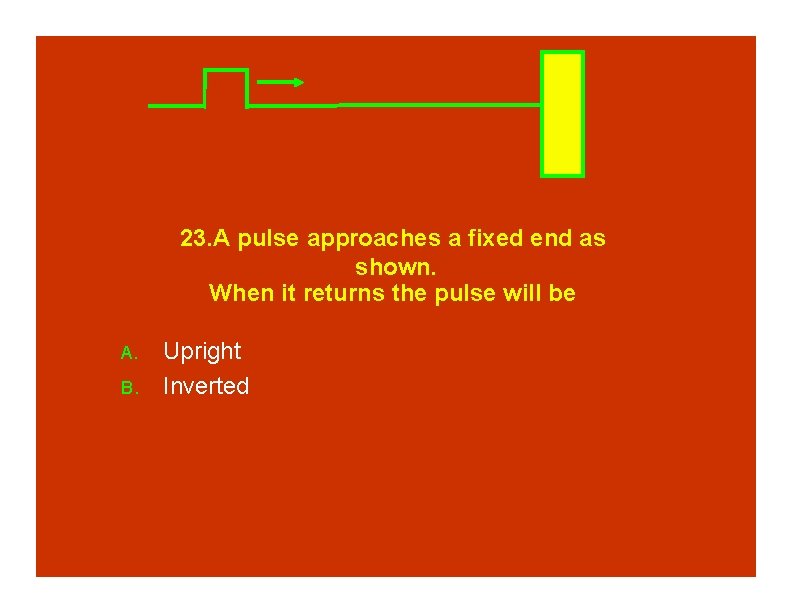
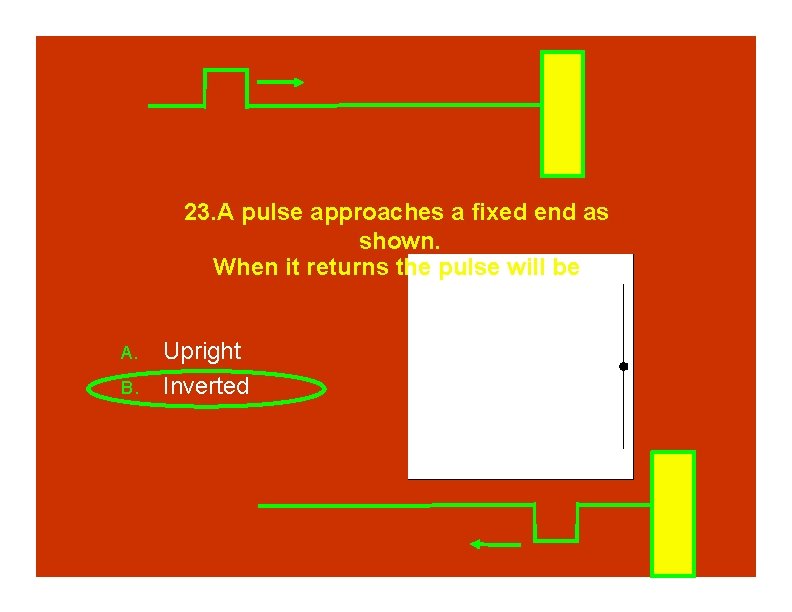
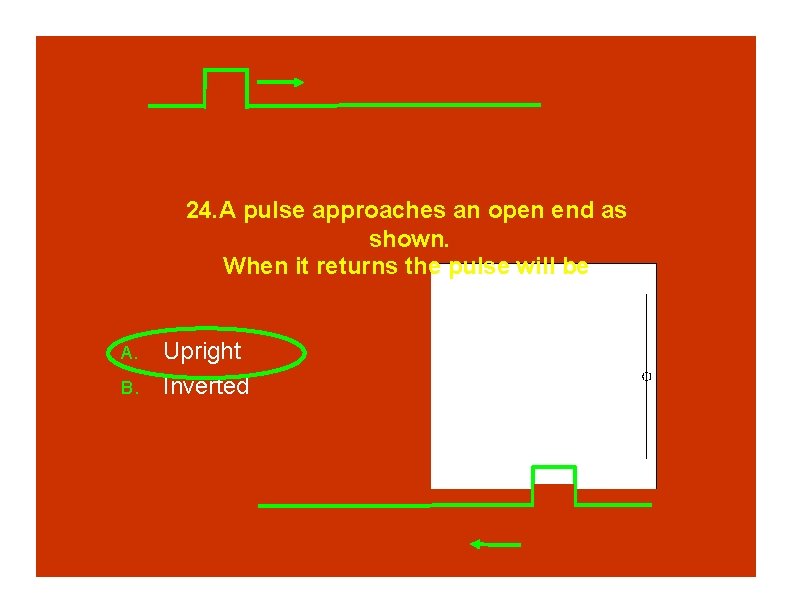
23. A pulse approaches a fixed end as shown. When it returns the pulse will be A. B. Upright Inverted

24. A pulse approaches an open end as shown. When it returns the pulse will be A. B. Upright Inverted

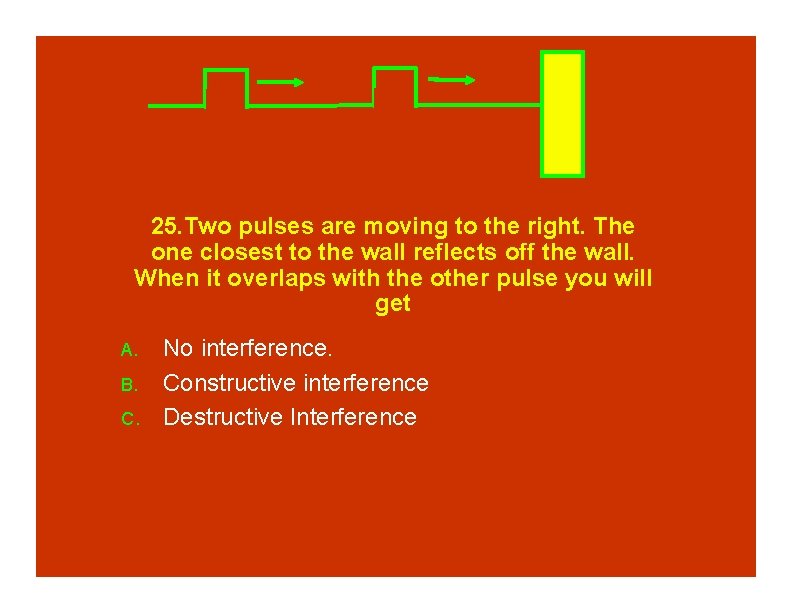
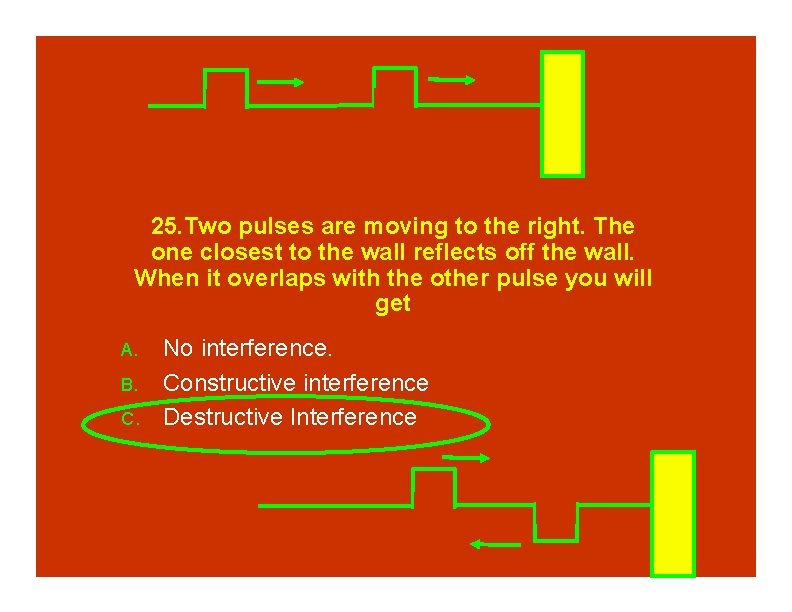
25. Two pulses are moving to the right. The one closest to the wall reflects off the wall. When it overlaps with the other pulse you will get A. B. C. No interference. Constructive interference Destructive Interference

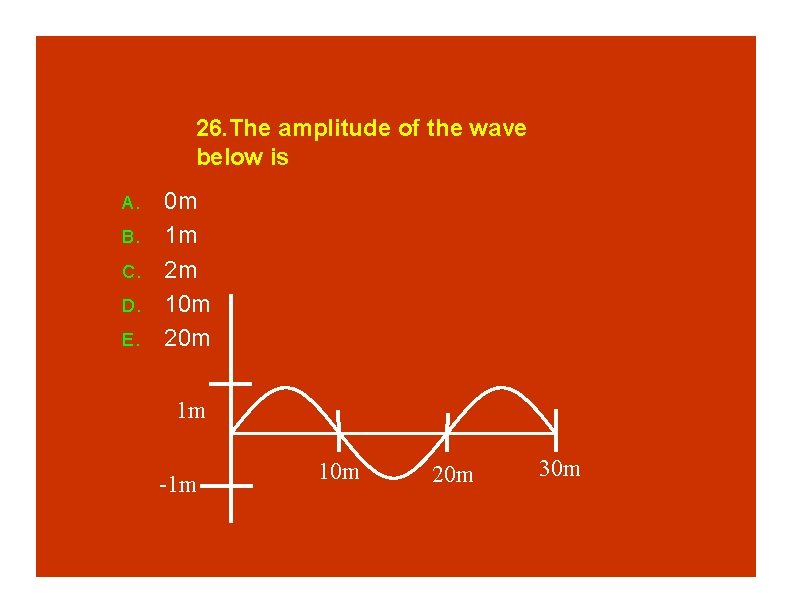
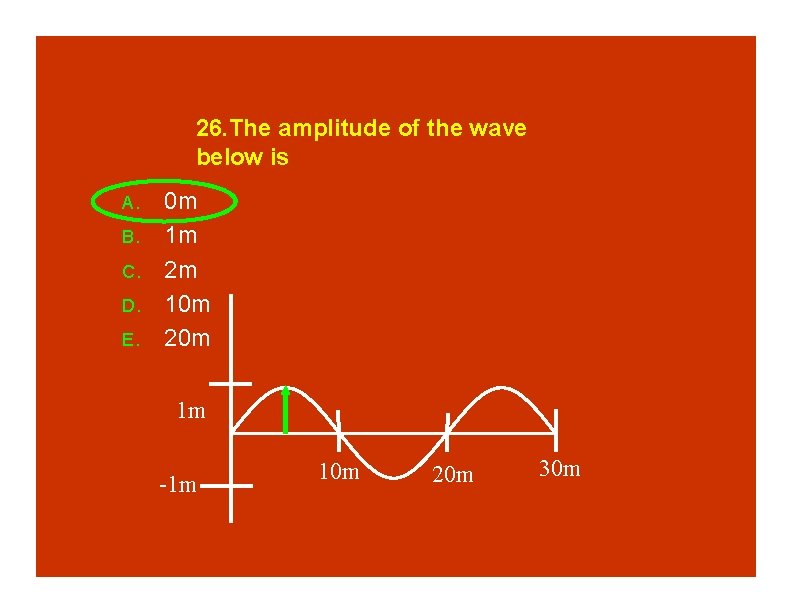
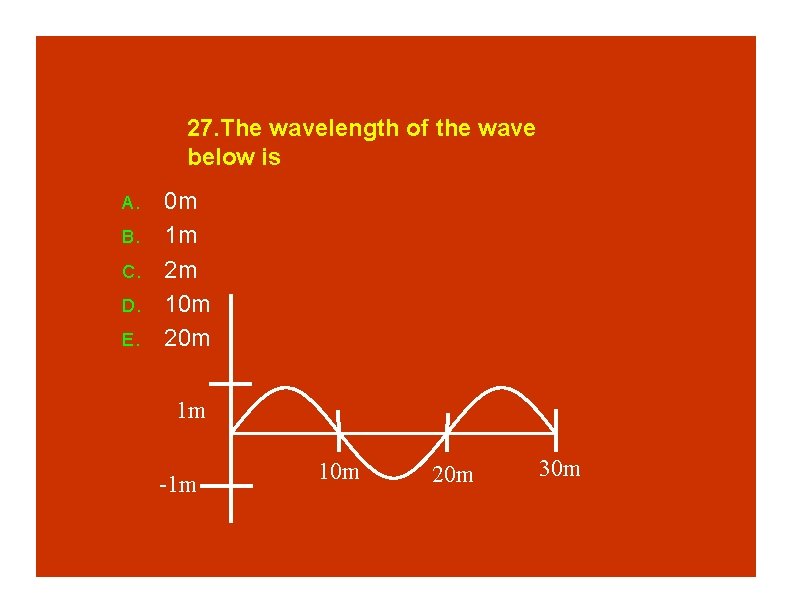
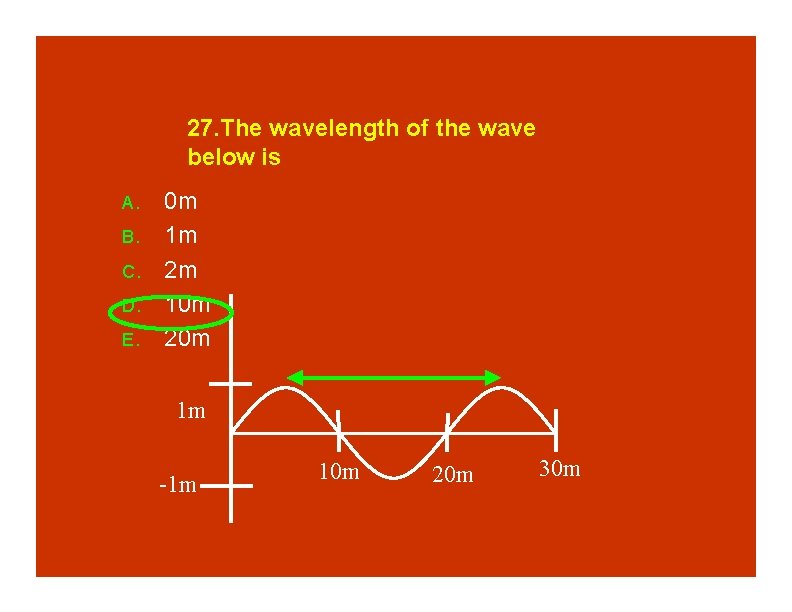
26. The amplitude of the wave below is A. B. C. D. E. 0 m 1 m 2 m 10 m 20 m 1 m -1 m 10 m 20 m 30 m

27. The wavelength of the wave below is A. B. C. D. E. 0 m 1 m 2 m 10 m 20 m 1 m -1 m 10 m 20 m 30 m

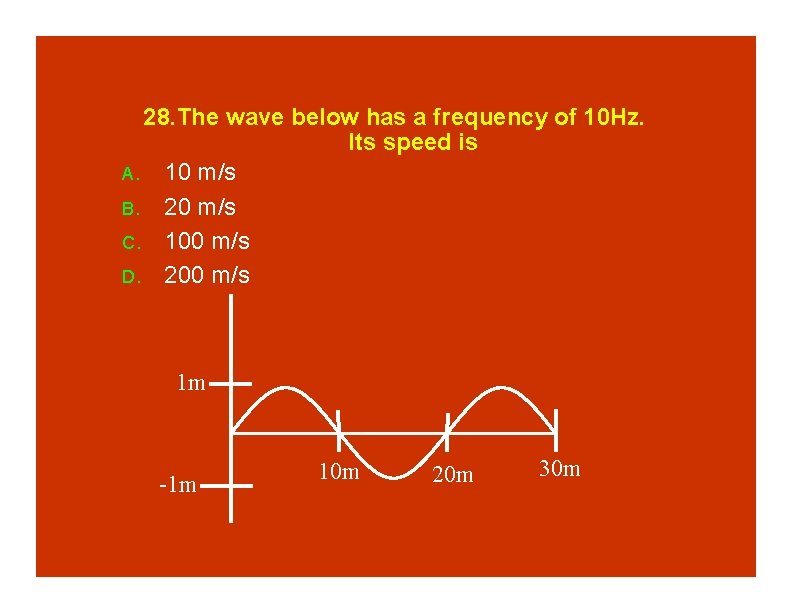
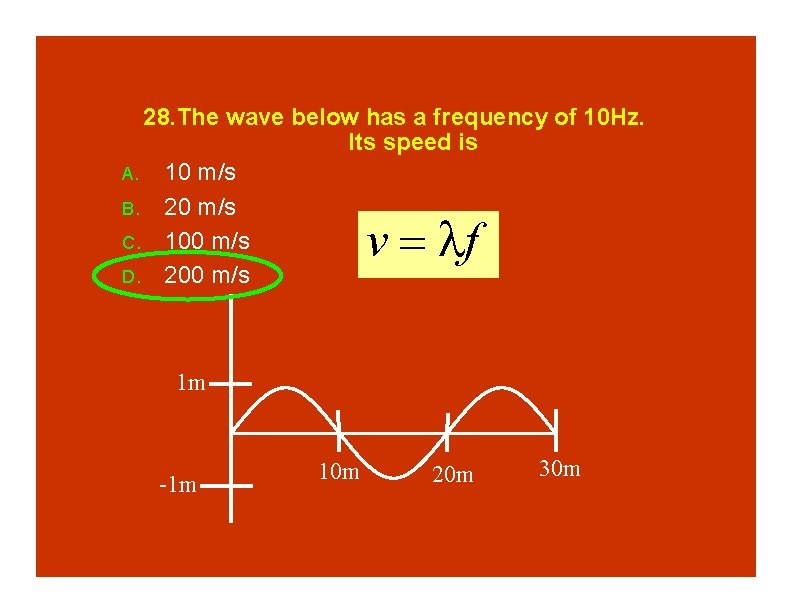
28. The wave below has a frequency of 10 Hz. Its speed is A. 10 m/s B. 20 m/s C. 100 m/s D. 200 m/s 1 m -1 m 10 m 20 m 30 m

28. The wave below has a frequency of 10 Hz. Its speed is A. 10 m/s B. 20 m/s C. 100 m/s D. 200 m/s v f 1 m -1 m 10 m 20 m 30 m

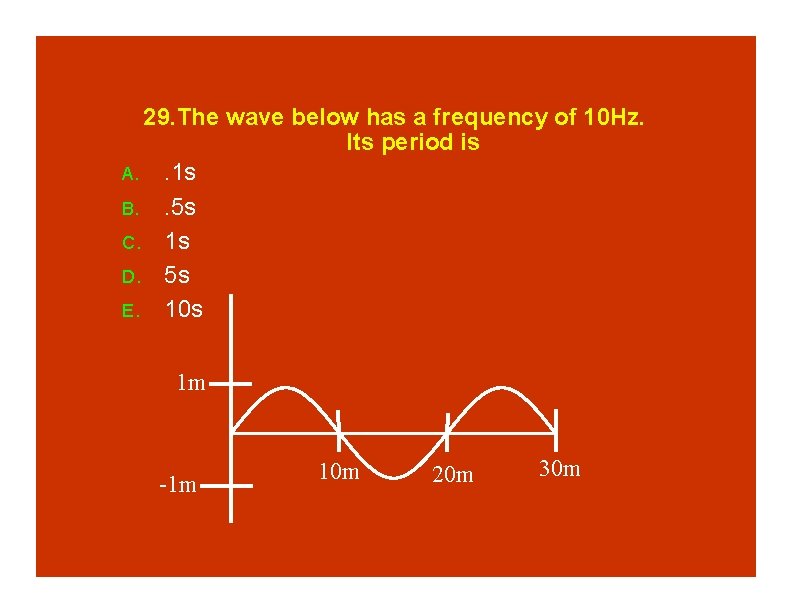
29. The wave below has a frequency of 10 Hz. Its period is A. . 1 s B. . 5 s C. 1 s D. 5 s E. 10 s 1 m -1 m 10 m 20 m 30 m

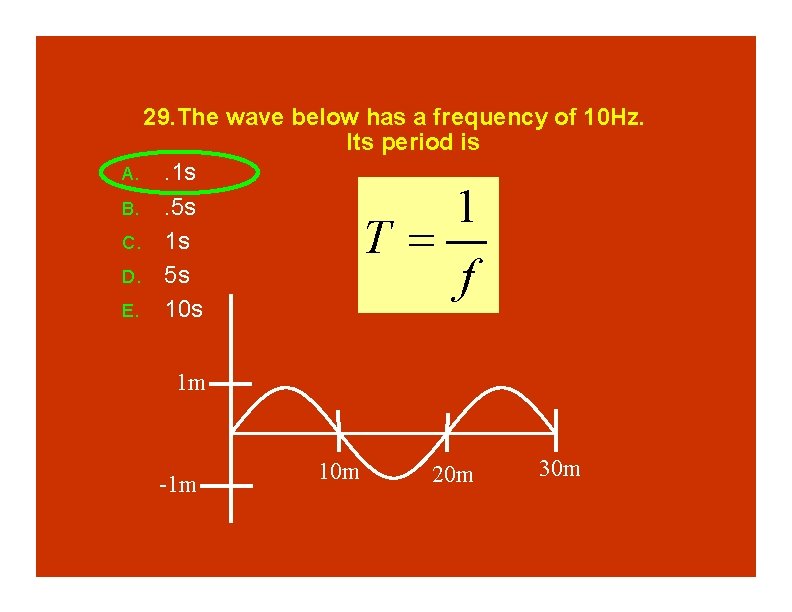
29. The wave below has a frequency of 10 Hz. Its period is A. . 1 s B. . 5 s C. 1 s D. 5 s E. 10 s 1 T f 1 m -1 m 10 m 20 m 30 m

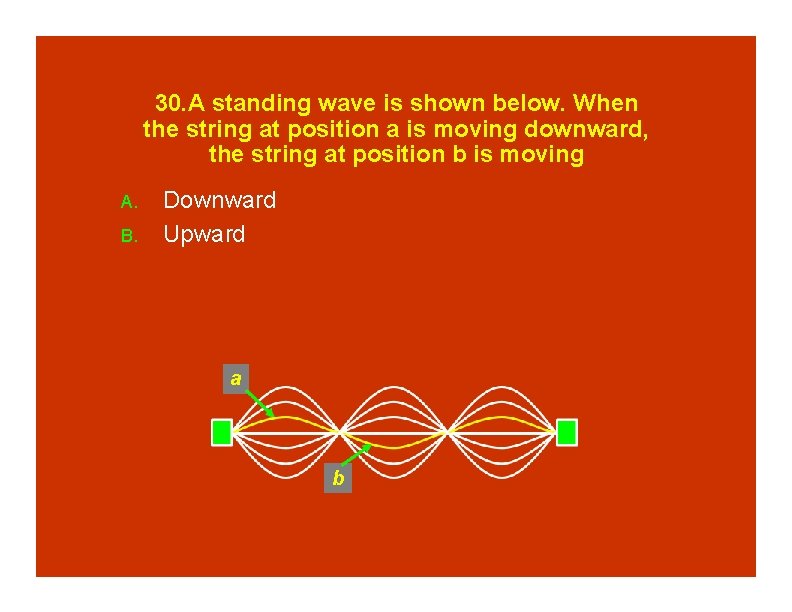
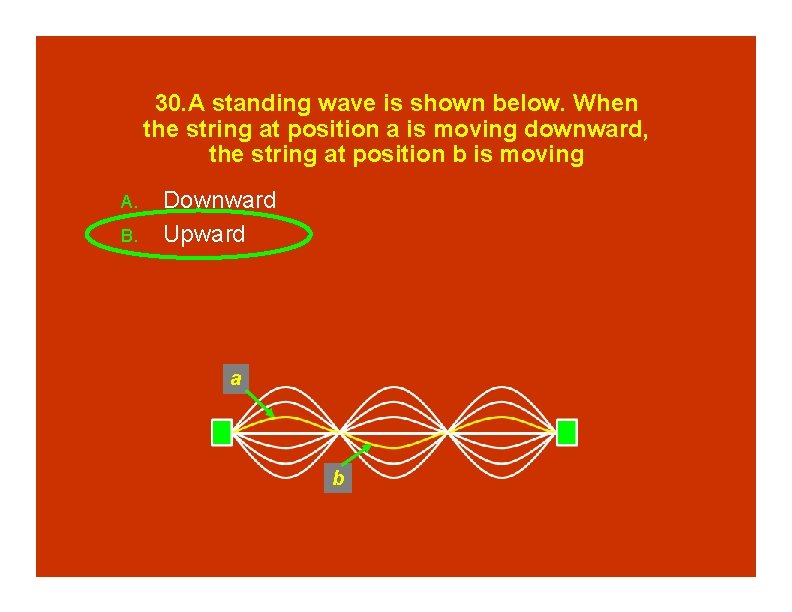
30. A standing wave is shown below. When the string at position a is moving downward, the string at position b is moving A. B. Downward Upward a b

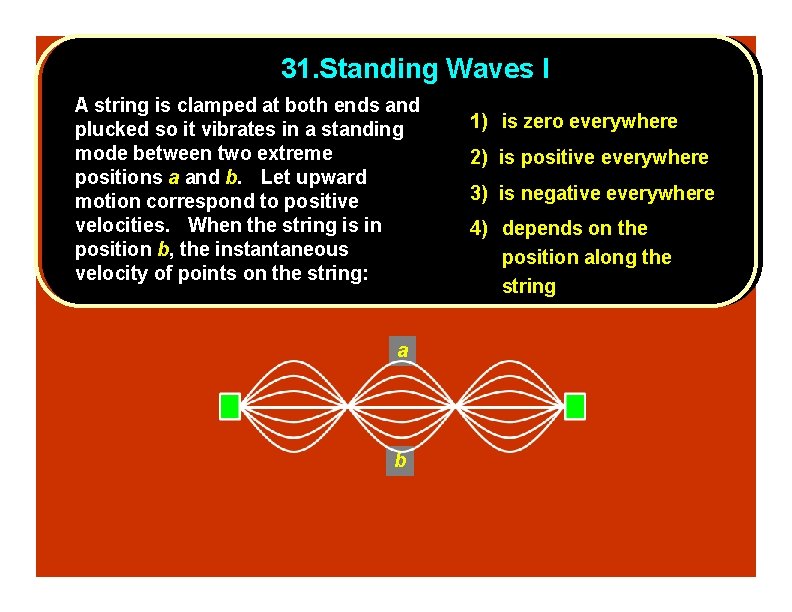
31. Standing Waves I A string is clamped at both ends and plucked so it vibrates in a standing mode between two extreme positions a and b. Let upward motion correspond to positive velocities. When the string is in position b, the instantaneous velocity of points on the string: a b 1) is zero everywhere 2) is positive everywhere 3) is negative everywhere 4) depends on the position along the string

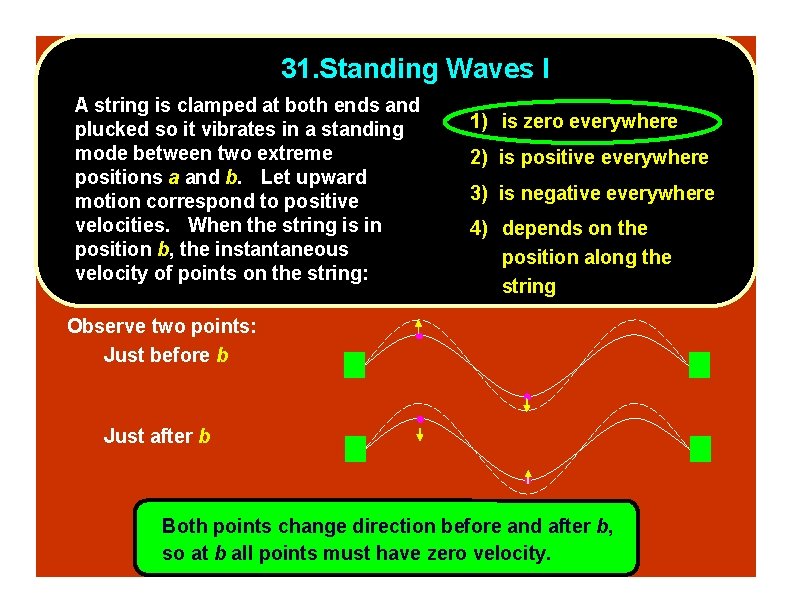
31. Standing Waves I A string is clamped at both ends and plucked so it vibrates in a standing mode between two extreme positions a and b. Let upward motion correspond to positive velocities. When the string is in position b, the instantaneous velocity of points on the string: 1) is zero everywhere 2) is positive everywhere 3) is negative everywhere 4) depends on the position along the string Observe two points: Just before b Just after b Both points change direction before and after b, so at b all points must have zero velocity.

32. Standing Waves II A string is clamped at both ends and plucked so it vibrates in a standing mode between two extreme positions a and b. Let upward motion correspond to positive velocities. When the string is in position c, the instantaneous velocity of points on the string: When the string is flat, all points are moving through the equilibrium position and are therefore at their maximum velocity. However, the direction depends on the location of the point. Some points are moving upwards rapidly, and some points are moving downwards rapidly. 1) is zero everywhere 2) is positive everywhere 3) is negative everywhere 4) depends on the position along the string a c b

33. Concep. Test 11. 1 c. Harmonic Motion III A mass on a spring in SHM has amplitude A and period T. How long does it take for the mass to travel a total distance of 6 A? 1) 1/2 T 2) 3/4 T 3) 1 1/4 T 4) 1 1/2 T 5) 2 T We have already seen that it takes one period T to travel a total distance of 4 A. An additional 2 A requires half a period, so the total time needed for a total distance of 6 A is 1 1/2 T. Follow-up: What is the net displacement at this particular time?

34. Concep. Test 11. 8 b. Period of a Pendulum II Two pendula have different lengths: one has length L and the other has length 4 L. How do their periods compare? 1) period of 4 L is four times that of L 2) period of 4 L is two times that of L 3) period of 4 L is the same as that of L 4) period of 4 L is one-half that of L 5) period of 4 L is one-quarter that of L The period of a pendulum depends on the length and the acceleration due to gravity. The length dependence goes as the square root of L, so a pendulum 4 times longer will have a period that is 2 times larger. T T == 22 ((LL//gg))