Do Now A car accelerates from a stop

Mean Value Theorem, Antiderivatives Section 4. 2 b

Mean Value Theorem If is continuous at every point of the closed interval and

Let me put it another way… The MVT says that somewhere between points A

More Practice with the MVT For each of the following, (a) show that the

A corollary of the MVT Functions with are Constant If at each point of

Which leads to another corollary Functions with Same Derivative Differ by a Constant If

Applying this new tool Find the function whose derivative is whose graph passes through

Definition: Antiderivative A function is an antiderivative of a function if for all in

More Practice Problems Find all possible functions with the given derivative.

More Practice Problems Find the function with the given derivative whose graph passes through

Slides: 15

Download presentation

Do Now A car accelerates from a stop to 45 m/sec in 4 sec. Explain why the car must have been accelerating at exactly 11. 25 m/sec 2 at some moment.

Mean Value Theorem, Antiderivatives Section 4. 2 b

Mean Value Theorem If is continuous at every point of the closed interval and differentiable at every point of its interior , then there is at least one point c in at which There is at least one point where the instantaneous slope is equal to the average slope…

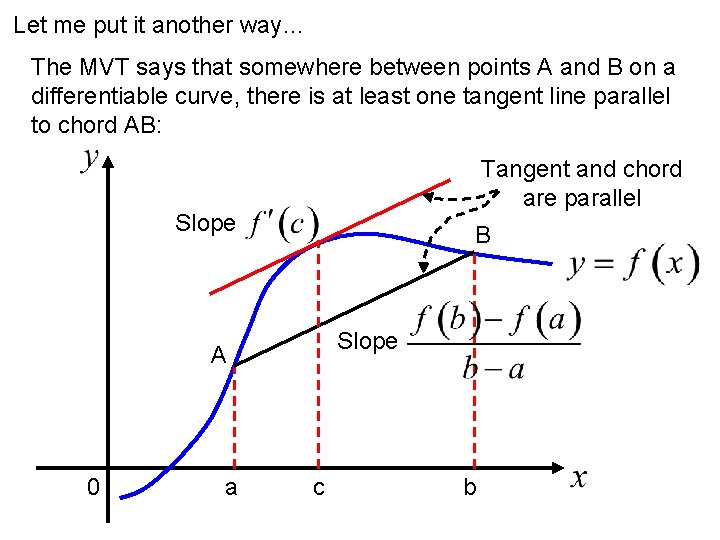
Let me put it another way… The MVT says that somewhere between points A and B on a differentiable curve, there is at least one tangent line parallel to chord AB: Tangent and chord are parallel Slope B Slope A 0 a c b

Do Now A car accelerates from a stop to 45 m/sec in 4 sec. Explain why the car must have been accelerating at exactly 11. 25 m/sec 2 at some moment. The average acceleration of the car over the interval is 45/4 = 11. 25 m/sec 2. By the MVT, the instantaneous acceleration of the car must have been that same value at least once during the interval…

More Practice with the MVT For each of the following, (a) show that the given function satisfies the hypotheses of the MVT on the given interval. (b) Find each value of c as a solution of the MVT. à The function is continuous on [0, 2] and differentiable on (0, 2) Can we interpret this result with a graph? ? ?

A corollary of the MVT Functions with are Constant If at each point of an interval I, then there is a constant for which for all in I.

Which leads to another corollary Functions with Same Derivative Differ by a Constant If at each point of an interval I, then there is a constant that for all in I. Let’s see this one graphically… à What if the derivative of two functions is 2 x? ? ? such

Applying this new tool Find the function whose derivative is whose graph passes through the point. and has the same derivative as So must equal Use the given point to identify C: (C a constant)

Definition: Antiderivative A function is an antiderivative of a function if for all in the domain of. The process of finding an antiderivative is called antidifferentiation.

More Practice Problems Find all possible functions with the given derivative.

More Practice Problems Find the function with the given derivative whose graph passes through the point P. All possible functions with this derivative: Solve for C: Final answer: