DNT 242 MACHINE MECHANISM ELEMENTS Chapter 6 LINKAGES

















- Slides: 20

DNT 242 – MACHINE MECHANISM ELEMENTS Chapter 6 LINKAGES AND MECHANISM

Chapter 6: LINKAGES AND MECHANISM What is a linkage?

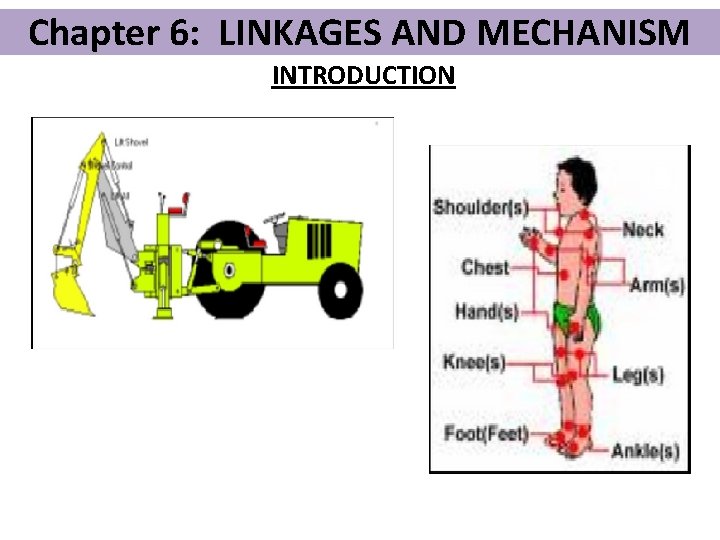
Chapter 6: LINKAGES AND MECHANISM INTRODUCTION q A mechanical linkage is a series of rigid links connected with joints to form a closed chain, or a series of closed chains. q Each link has two or more joints, and the joints have various degrees of freedom to allow motion between the links.

Chapter 6: LINKAGES AND MECHANISM INTRODUCTION q A linkage is called a mechanism if two or more links are movable with respect to a fixed link. q Mechanical linkages are usually designed to take an input and produce a different output, altering the motion, velocity, acceleration, and applying mechanical advantage. q A linkage designed to be stationary is called a structure.

Chapter 6: LINKAGES AND MECHANISM INTRODUCTION

Chapter 6: LINKAGES AND MECHANISM INTRODUCTION

Chapter 6: LINKAGES AND MECHANISM INTRODUCTION

Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM The minimum number of independent coordinates that define the displacement and deformation of the body.

Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM The minimum number of independent coordinates that define the displacement and deformation of the body

Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM THEORY • The most common linkages have one degree of freedom, meaning that there is one input motion that produces one output motion. • Most linkages are also planar, meaning all the motion takes place in one plane.

Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM THEORY • Spatial linkages (non-planar) are more difficult to design and therefore not as common. • Kutzbach-Gruebler's equation is used to calculate the degrees of freedom of linkages. The number of degrees of freedom of a linkage is also called its mobility.

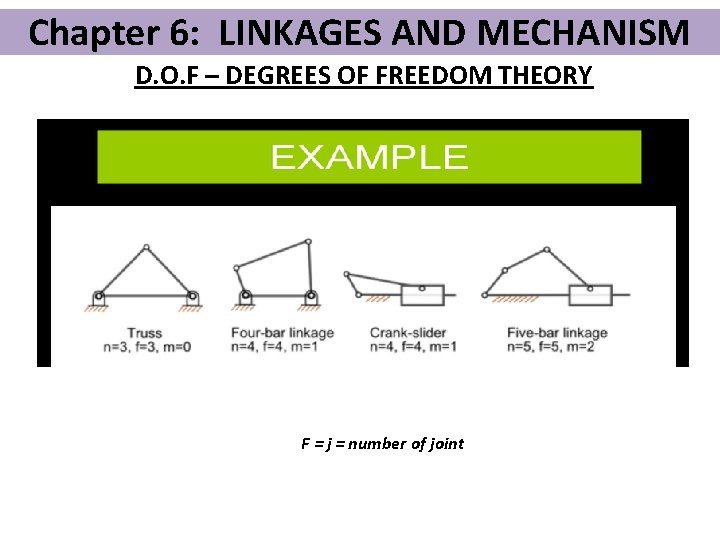
Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM THEORY v A simplified version of the Kutzbach-Gruebler's equation for planar linkages : m = mobility = degrees of freedom n = number of links (including a single ground link) j = number of one-degree-of-freedom kinematic pairs (pin or slider joints)

Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM THEORY When; m = 0; structure m = 1; mechanism with 1 DOF m = 2; mechanism with 2 DOF m < 0; redundant structure

Chapter 6: LINKAGES AND MECHANISM D. O. F – DEGREES OF FREEDOM THEORY F = j = number of joint

Chapter 6: LINKAGES AND MECHANISM Types of common joints: • Revolute or pin, one DOF rotation. Examples are; bushings, bearings, bolted joints, rivets and hinges. • Prismatic or slider, one or two DOF linear motion. Examples are; linear bearings, hydraulic cylinders, rollers and pistons. • Spherical or ball and socket, three DOF rotation, usually restricted to one DOF by other joints in the mechanism.

Chapter 6: LINKAGES AND MECHANISM Types of common joints: • Designers will synthesize a linkage by starting with the required output motion, mechanical advantage, velocity and acceleration. • A type of linkage is chosen and modified to deliver the required performance. • Each link is treated as a vector and the vectors can be combined into a system of equations because they form a loop. • The matrix is solved to create a closed form equation that relates input motion to output motion.

Chapter 6: LINKAGES AND MECHANISM Four Bar Linkage • A four bar linkage or simply a 4 -bar or four-bar is the simplest movable linkage. It consists of 4 rigid bodies (called bars or links), each attached to two others by single joints is the simplest movable linkage. • It consists of 4 rigid bodies (called bars or links), each attached to two others by single joints or pivots to form a closed loop. • Four-bars are simple mechanisms common in mechanical engineering machine design and fall under the study of kinematics.

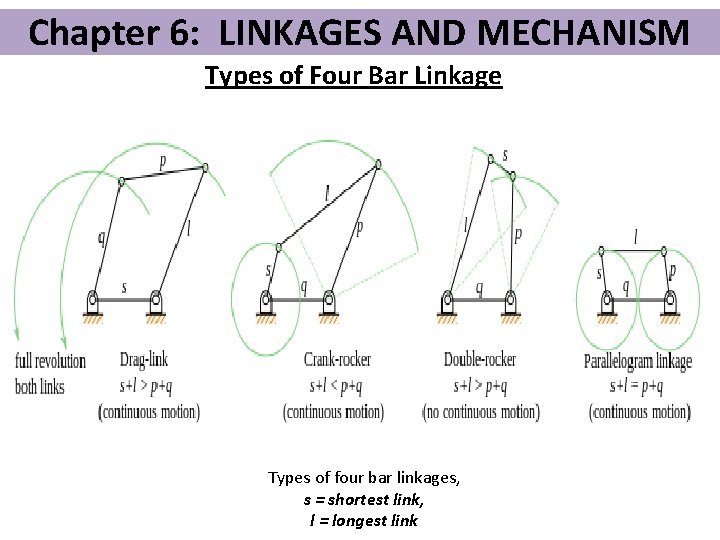
Chapter 6: LINKAGES AND MECHANISM Types of Four Bar Linkage Types of four bar linkages, s = shortest link, l = longest link

Chapter 6: LINKAGES AND MECHANISM Types of Four Bar Linkage Crank: A side link which rotates relative to the frame is called a crank. Rocker: Any link which does not rotate is called a rocker. Crank-rocker mechanism: In a four bar linkage, if the shorter side link rotates and the other one rocks (i. e. , oscillates), it is called a crank-rocker mechanism. Double-crank mechanism: In a four bar linkage, if both of the side links rotate, it is called a double-crank mechanism. Double-rocker mechanism: In a four bar linkage, if both of the side links rock, it is called a double-rocker mechanism.

THANK YOU