DNEM DEV Konu MATRSLER ve DETERMNANTLAR m ve

DÖNEM ÖDEVİ Konu : MATRİSLER ve DETERMİNANTLAR

m ve n pozitif tam sayılar olsun. İ=1, 2, 3. . . , m ve j=1, 2, 3. . , n için aij sayılarının meydana getirdiği ; şeklindeki dikdörtgensel tabloya m x n tipinde bir matris denir ve A=[ aij]m x n şeklinde gösterilebilir. Burada i ’ye satır indisi, j ’ye sütun indisi denir. aij ye de matrisin i inci satır , j inci sütundaki elemanı denir.

ÖRNEK : matrisi R de tanımlanmış 2 x 3 tipinde bir matristir. A= ÖRNEK A= : matrisi Z de tanımlanmış 3 x 4 tipinde bir matristir. Burada , ikinci satır dördüncü sütundaki eleman a 24 = -1 , üçüncü satır tür.

Bir matriste satır sayısı , sütun sayısına eşitse bu matrise kare matris denir. ÖRNEK A= : matrisi 3 x 3 tipinde karesel bir matristir.

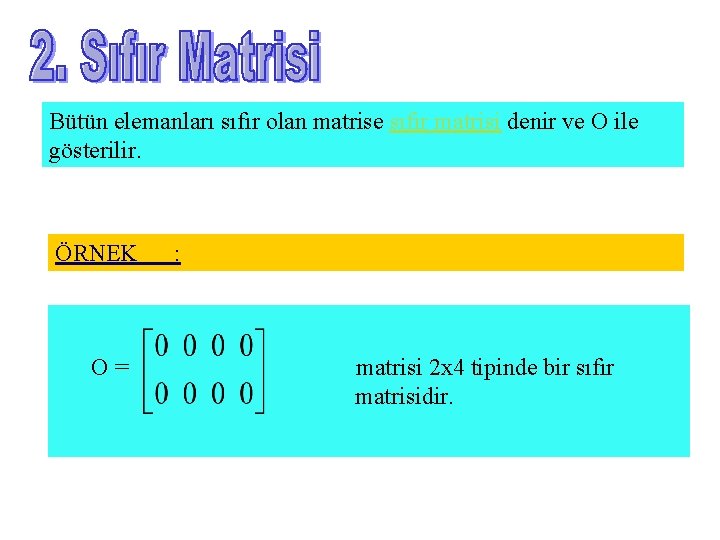
Bütün elemanları sıfır olan matrise sıfır matrisi denir ve O ile gösterilir. ÖRNEK O= : matrisi 2 x 4 tipinde bir sıfır matrisidir.

Birinci köşegen üzerindeki elemanlar 1 , bunların dışındaki elemanların tümü sıfır olan matrise birim matris denir. ile gösterilir. ÖRNEK = : matrisi 3 x 3 tipinde birim matristir.

Bir kare matriste, birinci köşegen üzerindeki elemanlardan en az birisi sıfırdan farklı olmak üzere diğer bütün elemanları sıfır ise bu matrise köşegen matrisi denir. ÖRNEK A= : matrisi 2 x 2 tipinde bir köşegen matristir.

Bir kare matriste , birinci köşegen üzerindeki elemanlar birbirinin aynısı olmak üzere diğer bütün elemanlar sıfır ise bu matrise skaler matris denir. ÖRNEK A= : matrisi 3 x 3 tipinde bir skaler matristir.

Satır sayısı bir olan matrise satır matrisi , sütun sayısı bir olan matrise de sütun matrisi denir. ÖRNEK A= B= : matrisi 1 x 4 tipinde bir satır matrisi , matrisi 3 x 1 tipinde bir sütun matrisidir.

A=[aij ]m x n , B=[ bij ]mxn iki matris olsun. A(i, j) için aij =bij ise A ve B matrisleri eşittir denir. A=B şeklinde gösterilir. Yani iki matrisin eşit olması için aynı tipten olmaları ve karşılıklı olarak aynı indisli elemanları birbirine eşit olmalıdır. ÖRNEK :

A = [aij] mxn , B = [ bij]mxn aynı tipten iki matris olsun. A+B = [aij]mxn + [ bij ]mxn = [aij + bij ]mxn olarak tanımlanır. Yani aynı tipten matrisler toplanabilir ve karşılıklı olarak aynı indisli elemanlar toplanıp aynı indisli yere yazılır. ÖRNEK :

1. Değişme özelliği vardır. A +B = B+A ‘dır. 2. Birleşme özelliği vardır. A + B + C = A +(B+C) = (A+B)+C ‘ dir. 3. Aynı tipten bir matrisle sıfır matrisinin toplamı bu matrise eşittir. Yani sıfır matrisi toplamaya göre etkisiz elemandır. A+O = O + A = A ‘dır.

Bir k skaları ile A = [aij ]mxn matrisinin çarpımı kx. A = kx[aij ]mxn = [ k. aij]mxn olarak tanımlanır. Yani bir matrisi k ile çarpmak demek matrisin bütün elemanlarını k ile çarpmak demektir. ÖRNEK :

A=[aij]mxn ve B=[bij]mxn iki matris olsun. A ile B nin çarpımı C olmak üzere , A x B = C [aij]mxn. [bij]nxp =[cij]mxp olur. Yani A matrisinin i inci satırı ile B matrisinin k ıncı sütununun karşılıklı elemanlarının çarpımlarının toplamı C matrisinin (i , k) ıncı elemanını verecektir. Bu yüzden iki matrisin çarpılabilmesi için birincinin sütun sayısının , ikincinin satır sayısına eşit olması gerekir. Çarpım matrisinin satır sayısı birinci matrisin satır sayısına , sütun sayısı ise ikinci matrisin sütun sayısına eşit olur.

ÖRNEK :

k bir skaler ve A , B , C matrisleri aşağıdaki işlemlerin her biri için tanımlı olsun. 1. Çarpma işleminin birleşme özelliği vardır. A. (B. C) = (A. B). C =A. B. C 2. Çarpma işleminin toplama işlemi üzerine dağılma özelliği vardır. A. (B+C) = A. B + A. C (B+C). A = B. A + C. A 3. k. (A. B) = (k. A). B = A. (k. B) dir.

4. In , nxn tipinde birim matris olmak üzere , A. In =In. A dır. 5. A , mxm tipinde bir kare matris olsun. A 0 = Im , A 1 = A , A 2 = A. A , . . An = A. An-1 dir. 6. Birim matrisin tüm kuvvetleri kendisine eşittir. In = I dır. 7. Çarpma işleminin değişme özelliği yoktur.

Determinant fonksiyonu , elemanları reel sayılar olan karesel matrisleri reel sayılara dönüştüren bir fonksiyondur. A = [ aij ]nxn ise determinant fonksiyonunun bu matristeki değeri A veya ‘det A’ ile gösterilir. A matrisi nxn tipinde ise A determinantı n inci mertebedendir denir. 1 x 1 tipinde A = [ aij ] matrisinin determinantı, A = a 11 ,

2 x 2 tipindeki bir matrisin determinantı , A = (a 11. a 22 – a 12. a 21) dir. ÖRNEK :

Üçüncü mertebeden bir determinantın değerini bulmak için ilk iki satır en alta yazılır , sağ köşegen üzerindeki elemanlar çarpılır ve toplanır. bundan sol köşegen üzerindeki elemanların çarpımlarının toplamı çıkartılır. = 1. 5. 9+2. 6. 7+3. 4. 8 -(3. 5. 7+1. 6. 8+2. 4. 9) =225 -225=0 dır.

Bir A = [aij]nxn matrisinde bir aij elemanın bulunduğu satır ve sütun atıldıktan sonra kalan matrisin determinantına aij nin minörü denir ve Mij ile gösterilir. (-1)i+j x Mij sayısına da aij nin kofaktörü ( eş çarpanı ) denir ve Aij ile gösterilir. 2 x 2 tipindeki bir matris A = [aij]2 x 2 olsun. A = a 11. A 11 + a 12. A 12 3 x 3 tipindeki bir matris A =[aij]3 x 3 olsun. A =a 11. A 11+ a 12. A 12+a 13. A 13

ÖRNEK :

nxn tipindeki bir matris A =[aij ]nxn olsun. A = a 11. A 11+a 12. A 12+a 13. A 13+. . +a 1 n. A 1 n Bu ifadelere bir determinantın 1 inci satıra göre açılımı denir. (2 inci , 3 üncü , . . . n inci satıra veya sütuna göre açılımda benzer şekilde tanımlanarak determinantın değeri hesaplanabilir. ) Determinant hesaplamak için determinant özellikleri kullanılarak bir satır veya sütunun elemanlarının bir kısmı sıfır yapıldıktan sonra bu satır veya sütuna göre açılım yapılabilir.

1. Karesel bir A matrisinin herhangi bir satır veya sütundaki bütün elemanları sıfır ise A = 0 dır. ÖRNEK :

2. Karesel bir matrisin iki satır veya sütunu kendi aralarında yer değiştirirse determinantın işareti değişir. Buna göre bir A matrisinin i inci satırı ile k ıncı satırı veya i inci sütunu ile k ıncı sütunu aralarında yer değiştirdiğinde elde edilen matris B ise B = - A dır. ÖRNEK :

3. Bir determinantı k sayısı ile çarpmak için bu determinantın sadece bir satırını veya sütununu k ile çarpmak gerekir. Buna göre bir A matrisi nxn tipinde ise k. A = kn. A olur. ÖRNEK :

4. Bir determinantın iki satırındaki veya sütunundaki elemanlar karşılıklı olarak orantılı ise bu determinantın değeri sıfırdır. ÖRNEK :

5. İki matrisin çarpımının determinantı , her iki matrisin determinantları çarpımına eşittir. nxn tipinde iki matris A ve B olsun. A. B = A. B olur. ÖRNEK :

6. bir determinantın bir satırındaki elemanların k katı başka bir satıra veya bir sütundaki elemanların k katı başka bir sütuna karşılıklı olarak eklenirse determinantın değeri değişmez. ÖRNEK : yukarıdaki işlemde 2 nci satırın 8 katı 1 nci satıra eklendi.

Bir A matrisinin satırlarının sütun , sütunlarının satır yapılması ile elde edilen matrise A matrisinin transpozu (devriği) denir ve AT ile gösterilir. ÖRNEK :

1. (A+B)T=AT+BT 2. (AT)T=A 3. (k. A)T=k. AT 4. (A. B)T=BT. AT 5. 6. (AT)-1 = (A-1)T 7. A karesel bir matris olmak üzere; AT = A ise A ya simetrik matris , AT = -A ise A ya anti simetrik matris , AT = A-1 ise A ya ortogonal matris denir.

ÖRNEK : matrisinin rankını bulalım.

ÇÖZÜM : A matrisi 3 x 2 tipinde olduğundan karesel matrisleri en çok 2 x 2 mertebesindedir.

ÖRNEK : matrisinin ek matrisini bulalım.

ÇÖZÜM : A 11=4, A 12 =-3 , A 13= 1 A 21=-8, A 22= 4 , A 23=-2 A 31= 6 , A 32= -3 , A 33=1 olduğundan

A, nxn tipinde bir matris olsun; A. B =B. A = In olacak şekilde bir B matrisi varsa , B ye A nın çarpmaya göre tersi denir ve A-1 ile gösterilir. nxn tipindeki bir matris için; A-1=1/ . Ek(A) dır.