DNA Sequence Alignment DISP Laboratory Graduate Institute of

DNA Sequence Alignment DISP Laboratory Graduate Institute of Communication Engineering National Taiwan University, Taipei, Taiwan (ROC) Speaker: Che-Ming Hu Adviser : Prof. Jian-Jiun Ding National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 1

Outline � Motivations � Introduction to DNA sequences � Sequence alignment algorithm ◦ ◦ Dynamic Programming Algorithm FASTA BLAST UDCR �CUDCR � Conclusion � Reference National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 2

Motivation � Huge amount of sequences � Too much computation time National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 3

Introduction to DNA sequence(1) � DNA ◦ ◦ Sequence Assembly Shotgun Sequencing Greedy algorithm Issues of shotgun sequencing Sequence alignment National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 4

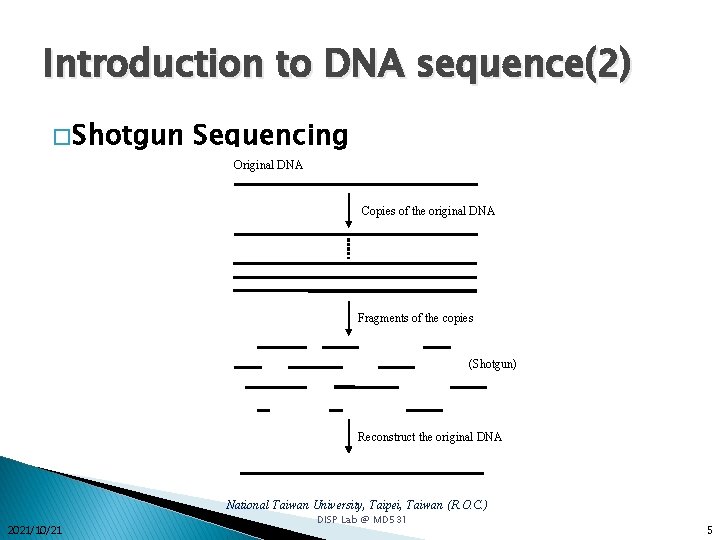
Introduction to DNA sequence(2) � Shotgun Sequencing Original DNA Copies of the original DNA Fragments of the copies (Shotgun) Reconstruct the original DNA National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 5

Introduction to DNA sequence(3) � Greedy ◦ ◦ algorithm Step 1. Calculate pair-wise alignments of all fragments. Step 2. Choose two fragments with the largest overlap. Step 3. Merge the chosen fragments. Step 4. Repeat step 2 and 3 until there is not any fragment which can be merged. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 6

Introduction to DNA sequence(4) � Issues ◦ ◦ of shotgun sequencing The errors in fragments. The unknown orientation of a fragment. Gaps in fragment coverage. Repeats in fragments. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 7

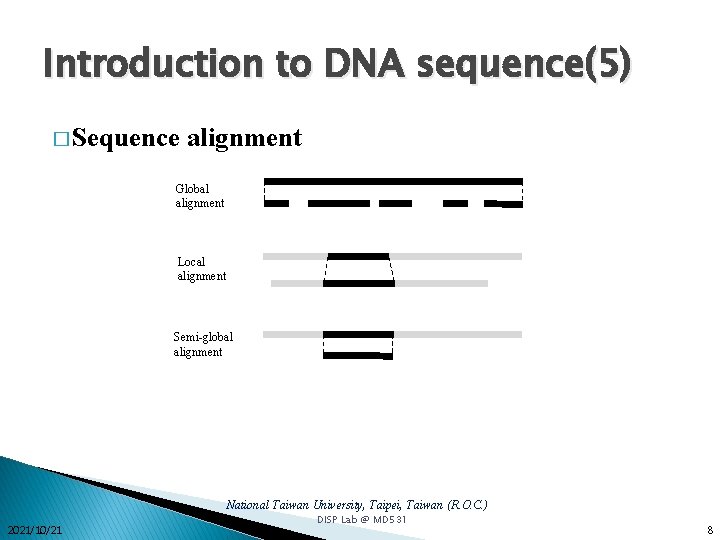
Introduction to DNA sequence(5) � Sequence alignment Global alignment Local alignment Semi-global alignment National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 8

Dynamic Programming(1) � The edit distance between two strings � String similarity method National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 9

Dynamic Programming(2) � The edit distance between two strings National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 10

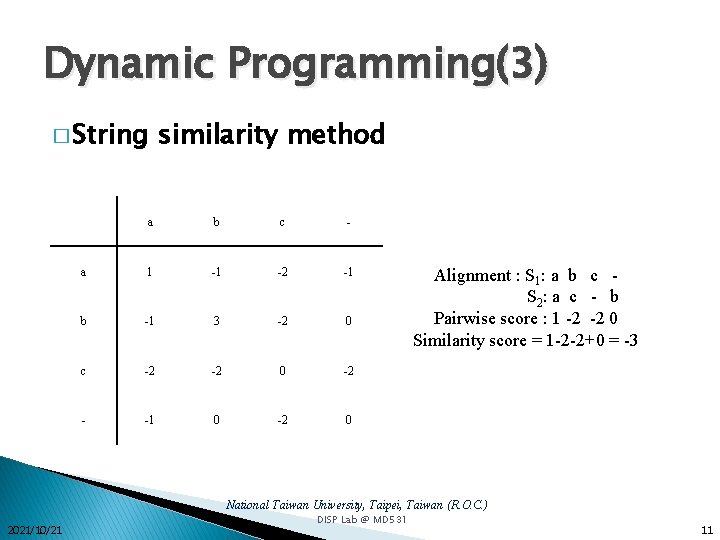
Dynamic Programming(3) � String similarity method a b c - a 1 -1 -2 -1 b -1 3 -2 0 c -2 -2 0 -2 - -1 0 -2 0 Alignment : S 1: a b c S 2 : a c - b Pairwise score : 1 -2 -2 0 Similarity score = 1 -2 -2+0 = -3 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 11

Dynamic Programming(4) � The recurrence relation � Tabular computation � The traceback National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 12

Dynamic Programming(5) � The recurrence relation ◦ Initial condition �D(i, 0)=i (the first column) �D(0, j)=j (the first row) ◦ recurrence relation �D(i, j)=min[D(i-1, j)+1, D(i, j-1)+1, D(i-1, j-1)+t(i, j)] �where � Here is a example: ◦ S 1=‘vintner’; S 2=‘writers’ National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 13

Dynamic Programming(6) � Initial condition �D(i, 0)=i �D(0, j)=j D(i, j) S 2 w r i t e r s S 1 0 1 2 3 4 5 6 7 v 1 i 2 n 3 t 4 n 5 e 6 r 7 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 14

Dynamic Programming(7) � Tabular computation ◦ D(i, j)=min[D(i-1, j)+1, D(i, j-1)+1, D(i-1, j-1)+t(i, j)] D(i, j) S 2 w r i t e r s S 1 0 1 2 3 4 5 6 7 v 1 1 2 3 4 5 6 7 i 2 2 3 4 5 6 n 3 3 3 4 5 6 t 4 4 3 4 5 6 n 5 5 4 4 5 6 e 6 6 5 4 5 6 r 7 7 6 5 4 5 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 15

Dynamic Programming(8) � The traceback ◦ Set a pointer from (i, j) to cell (i, j-1) , denoted by if D(i, j)= D(i, j-1)+1 ◦ Set a pointer from (i, j) to cell (i-1, j) , denoted by if D(i, j)= D(i-1, j)+1 ◦ Set a pointer from (i, j) to cell (i-1, j-1) , denoted by if D(i, j)= D(i-1, j-1)+t(i. j) ◦ Where, National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 16

Dynamic Programming(9) � Simulation(1) ◦ Number “ 1” in cell represent the route from right to left, denote by ◦ Number “ 2” in cell represent the route from down to up, denote by ◦ Number “ 3” in cell represent the route from rightdown to left-up, denote by National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 17

Dynamic Programming(13) � Simulation(2) The same similarity score !!! National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 18

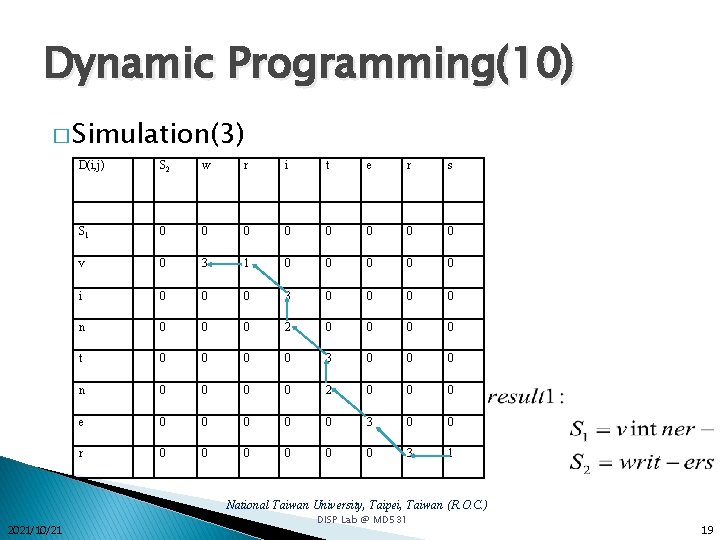
Dynamic Programming(10) � Simulation(3) D(i, j) S 2 w r i t e r s S 1 0 0 0 0 v 0 3 1 0 0 0 i 0 0 0 3 0 0 n 0 0 0 2 0 0 t 0 0 3 0 0 0 n 0 0 2 0 0 0 e 0 0 0 3 0 0 r 0 0 0 3 1 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 19

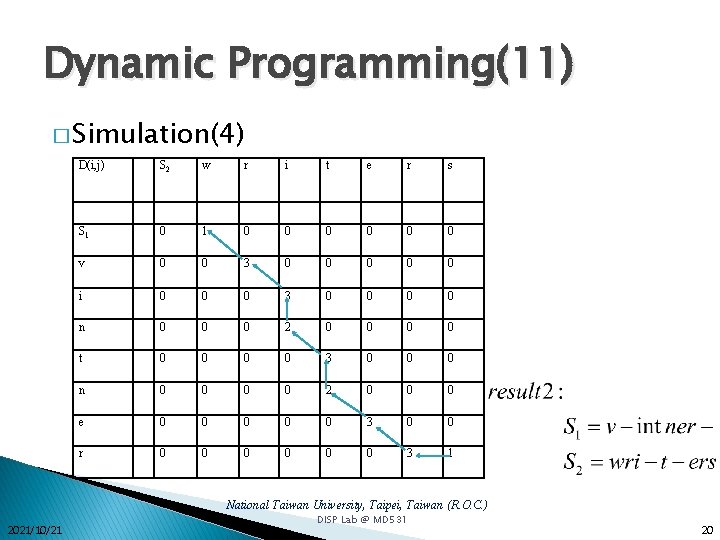
Dynamic Programming(11) � Simulation(4) D(i, j) S 2 w r i t e r s S 1 0 0 0 0 v 0 0 3 0 0 0 i 0 0 0 3 0 0 n 0 0 0 2 0 0 t 0 0 3 0 0 0 n 0 0 2 0 0 0 e 0 0 0 3 0 0 r 0 0 0 3 1 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 20

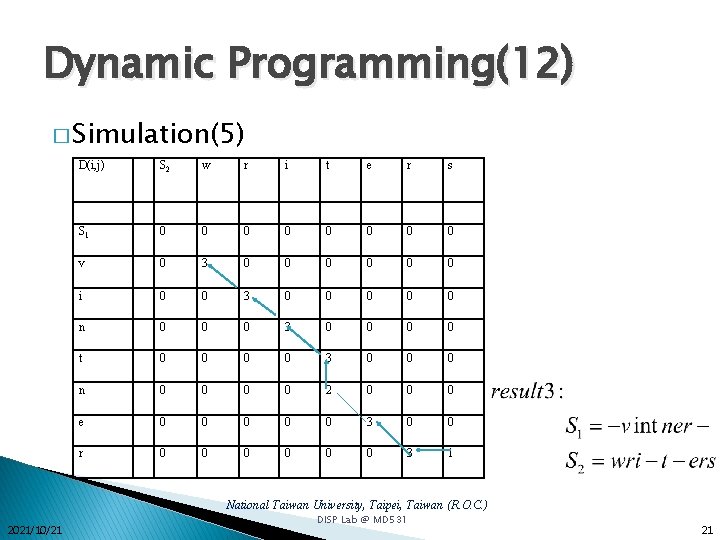
Dynamic Programming(12) � Simulation(5) D(i, j) S 2 w r i t e r s S 1 0 0 0 0 v 0 3 0 0 0 i 0 0 3 0 0 0 n 0 0 0 3 0 0 t 0 0 3 0 0 0 n 0 0 2 0 0 0 e 0 0 0 3 0 0 r 0 0 0 3 1 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 21

FASTA(1) � Only search for the consecutive identities of length k � More faster than dynamic program National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 22

FASTA(2) � � � STEP 1. Establish the lookup table (or Hash table) to show the positions of the k-tuple words in a sequence STEP 2. Use hashing to reveal a region of alignment between two sequences STEP 3. Find the 10 best diagonal regions. STEP 4. Keep only the most high-scoring diagonal regions. STEP 5. Try to join these remained diagonal regions into a longer alignment. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 23

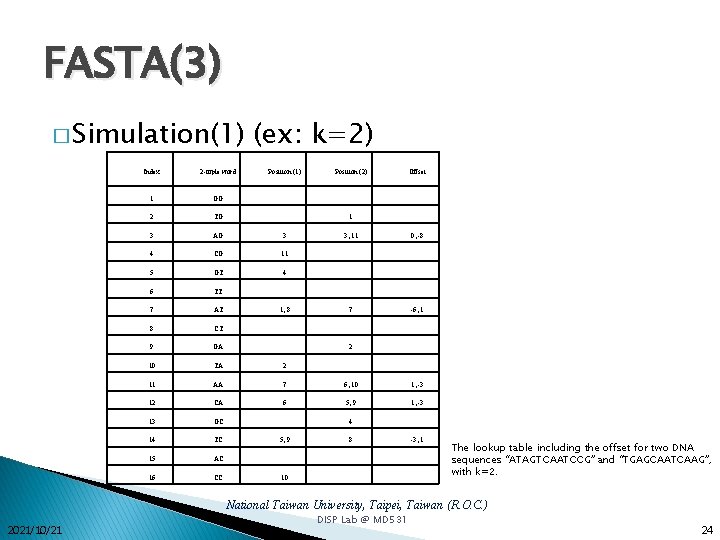
FASTA(3) � Simulation(1) (ex: k=2) Index 2 -tuple word Position (1) Position (2) Offset 1 GG 2 TG 3 AG 3 4 CG 11 5 GT 4 6 TT 7 AT 8 CT 9 GA 10 TA 2 11 AA 7 6, 10 1, -3 12 CA 6 5, 9 1, -3 13 GC 14 TC 15 AC 16 CC 1 1, 8 3, 11 0, -8 7 -6, 1 2 4 5, 9 8 10 -3, 1 The lookup table including the offset for two DNA sequences “ATAGTCAATCCG” and “TGAGCAATCAAG”, with k=2. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 24

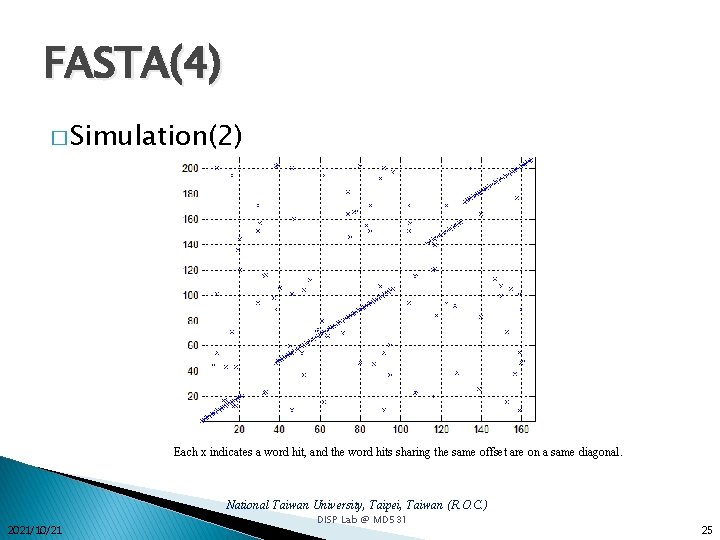
FASTA(4) � Simulation(2) Each x indicates a word hit, and the word hits sharing the same offset are on a same diagonal. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 25

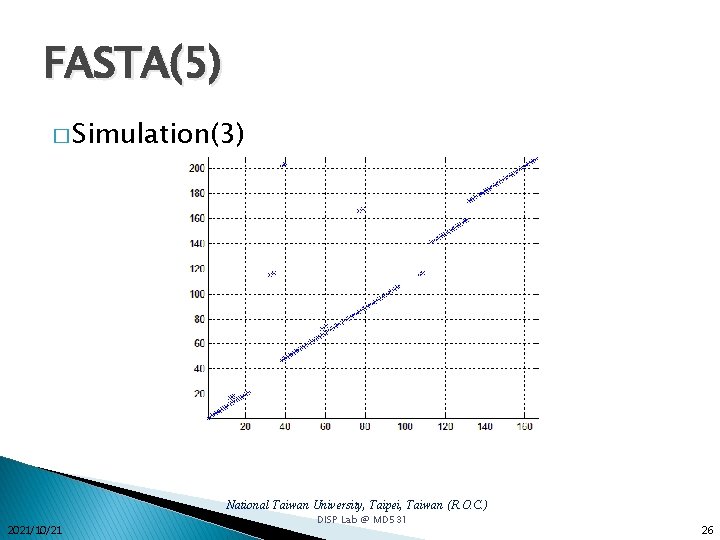
FASTA(5) � Simulation(3) National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 26

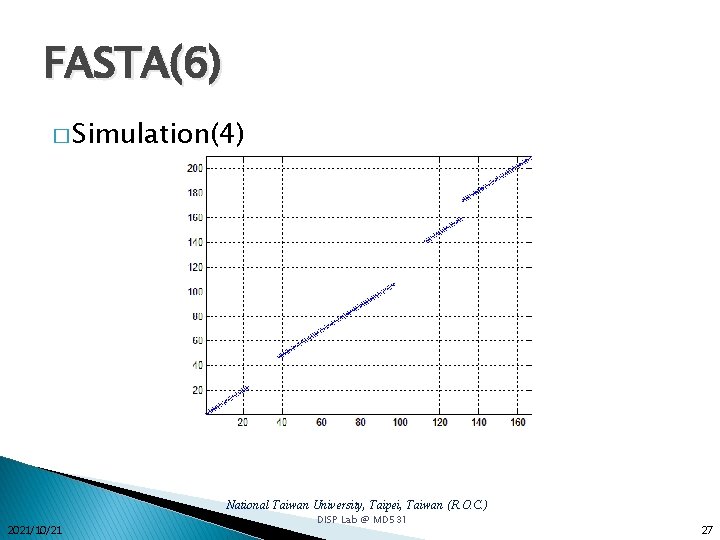
FASTA(6) � Simulation(4) National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 27

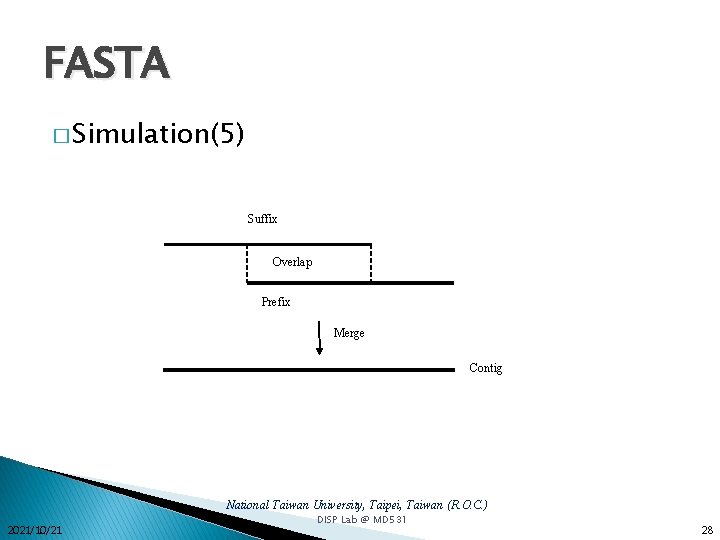
FASTA � Simulation(5) Suffix Overlap Prefix Merge Contig National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 28

BLAST(1) Similar to FASTA � Major difference with FASTA is: � ◦ choose the relative high-scoring word National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 29

BLAST(2) � Take 3 for example ◦ For example: ◦ the score obtained by comparing PQG with PEG and PQA is 15 and 12, respectively. ◦ While T is 13, PEG is kept and PQA is abandoned. Query sequence: PQGEFG Word 1: PQG Word 2: QGE Word 3: GEF Word 4: EFG National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 30

BLAST(3) Query sequence: R P P Q G L F Database sequence: D P P E G V V Exact match is scanned. Score: -2 7 7 2 6 1 -1 HSP Maximal aggregate score = 7+7+2+6+1 = 23 National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 31

BLAST(4) � Original BLAST � New BLAST (Gapped BLAST) ◦ more sensitive at augmented speed National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 32

UDCR(1) � Unitary Discrete Correlation (UDCR) Algorithm � A novel algorithm National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 33

UDCR(2) � Unitary Mapping � Discrete Correlation National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 34

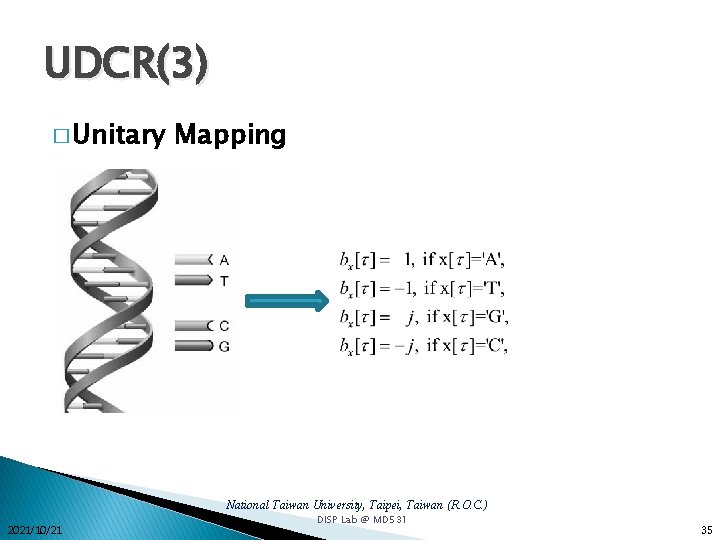
UDCR(3) � Unitary Mapping National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 35

UDCR(4) � Discrete Correlation ◦ Definition: �s [n] (similarity index): �s 1[n] (pair-similarity index): �s 2[n] (pair-different index): �x, y are two DNA sequence: National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 36

UDCR(5) � s[n] � (similarity index) ( xn[ ] = x[ + n], = 0, 1, …. . , M 1, n = -M+1, -M+2, …. . , N 1. ) ◦ the number of nucleotides of xn that satisfy xn[ ] = y[ ]. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 37

UDCR(6) � s 1[n] (pair-similarity index): ◦ the number of nucleotides of xn that satisfy bx, n[ ] = by[ ], ◦ where bx, n and by are the unitary value representations of xn and y, respectively ◦ In fact, bx, n[ ] = by[ ] means that x[n+ ] is different from y[ ] but they belong to the same pair (A-T pair or G-C pair). National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 38

UDCR(7) � s 2[n] (pair-different index): ◦ the number of nucleotides of xn that satisfy bx, n[ ] = j by[ ] ◦ (i. e. , x[n+ ] is quite different from y[ ]. Thus they do not belong to the same pair). National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 39

UDCR(8) National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 40

UDCR(9) � Simulation(1) ◦ x = ‘GTAGCTGAAC’; ◦ y = ‘AACTGAA’, ◦ Then, N = 15 and M = 7. �bx = [j, 1, 1, j, 1, 1, j, 1, j, 1, 1, j], �by = [1, 1, j, 1, j, 1, 1]. �z 1= [j, -1+j, 1, 1+j, -1 -j, -3+j 2, j 3, 6+j, 1 -j 4, -4 -j 3, -4+j 3, 2+j 5, 7, 2 -j 5, -3 -j 3, -3+j 2, 1+j 3, 3, 1 -j, -j], �z 2= [ 1, 0, 3, 2, 1, 0, 1, 1, 5, 1, 1, 3, 7, 3, 0, 1, 2, 3, 0, 1] ◦ Note that National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 41

UDCR(10) � Simulation(2) � Since s[7]=L 7=M=7, we can conclude that the 7 -length subsequence starting from s[7] ◦ (i. e. , {s[7], s[8], …. , s[13]}) ◦ x =‘GTAGCTGAAC’, y= ‘AACTGAA’. ◦ y 7: y shifted 7 entries rightward) National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 42

UDCR(11) � Simulation(3) � Since s[2]=L 2=M=7, we can conclude that the 7 -length subsequence starting from s[2] ◦ (i. e. , {s[2], s[3], …. , s[8]}) � x =‘GTAGCTGAAC’, y= ‘AACTGAA’. � y 2: y shifted 2 entries rightward) National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 43

UDCR(12) � Simulation(4) � � Since S[12]=L 12=N-n=15 -12=3, We can conclude that the 3 -length suffix of x matches the 3 length prefix of y ◦ x =‘GTAGCTGAAC’, y= ‘AACTGAA’. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 44

UDCR(13) � Simulation(5) � � Since S[-4]=L-4=M+n=7+(-4)=3, We can conclude that the 3 -length prefix of x matches the 3 length sufffix of y ◦ x= ‘GTAGCTGAAC’, y =‘AACTGAA’. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 45

Conclusion � By using UDCR, we can derive the result and this algorithm really saves us a lot of computation time. � In addition, we can combine UDCR and DP algorithm to a new algorithm called CUDCR. � The advantage of CUDCR is saving more time and as accurate as UDCR. � Use NTT instead of DFT due to less computation. National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 46

Reference � [1] Soo-Chang Pei, Jian-Jiun Ding “Sequence Comparison and Alignment by Discrete Correlations, Unitary Mapping, and Number Theoretic Transforms” � [2] Kang-Hua Hsu, ” Introduction to sequence comparison and alignment” � [3]Michael S. Waterman, ”Introduction to computational biology” � [4]Dan Dusfield, ”Algorithm on Strings, Trees, and Sequences” � [5]Setubal, Meidanis, “Introduction to Computational Molecular Biology” National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 47

Thank you National Taiwan University, Taipei, Taiwan (R. O. C. ) 2021/10/21 DISP Lab @ MD 531 48