DNA Sequence Alignment A dynamic programming algorithm Some

DNA Sequence Alignment A dynamic programming algorithm Some ideas stole from Winter 1996 offering of 590 BI at http: //www/education/courses/590 bi/98 wi/ See Lecture 2 by Prof. Ruzzo. Or try current quarter of CSE 527. Those slides are more detailed and biologically accurate.

DNA Sequence Alignment (aka “Longest Common Subsequence”) • The problem – What is a DNA sequence? – DNA similarity – What is DNA sequence alignment? – Using English words • The Naïve algorithm • The Dynamic Programming algorithm • Idea of Dynamic Programming

What is a DNA sequence • DNA: string using letters A, C, G, T – Letter = DNA “base” – e. g. AGATGGGCAAGATA • DNA makes up your “genetic code”

DNA similarity • DNA can mutate. – Change a letter • AACCGGTT ATCCGGTT – Insert a letter • AACCGGTT ATAACCGGTT – Delete a letter • AACCGGTT • A few mutations makes sequences different, but “similar”

Why is DNA similarity important • New sequences compared to existing sequences • Similar sequences often have similar function • Most widely used algorithm in computational biology tools – e. g. BLAST at http: //www. ncbi. nlm. nih. gov/BLAST/

What is DNA sequence alignment? • Match 2 sequences, with underscore ( _ ) wildcards. • Best Alignment minimum underscores (slight simplification, but okay for 326) ACCCGTTT • e. g. TCCCTTT Best alignment: (3 underscores) A_CCCGTTT _TCCC_TTT

Moving to English words zasha ashes zash__a _ashes_

Naïve algorithm • Try every way to put in underscores • If it works, and is best so far, record it. • At end, return best solution.

Naïve Algorithm – Running Time • Strings size M, N:

Dynamic Approach – A table • Table(x, y): best alignment for first x letters of string 1, and first y letters of string 2 • Decide what to do with the end of string, then look up best alignment of remainder in Table.

e. g. ‘a’ vs. ‘s’ • “zasha” vs. “ashes”. 2 possibilities for last letters: – (1) match ‘a’ with ‘_’: • best_alignment(“zash”, ”ashes”)+1 – (2) match ‘s’ with ‘_’: • best_alignment(“zasha”, ”ashe”)+1 • best_alignment(“zasha”, ”ashes”) =min(best_alignment(“zash”, ”ashes”)+1, best_alignment(“zasha”, ”ashe”)+1)

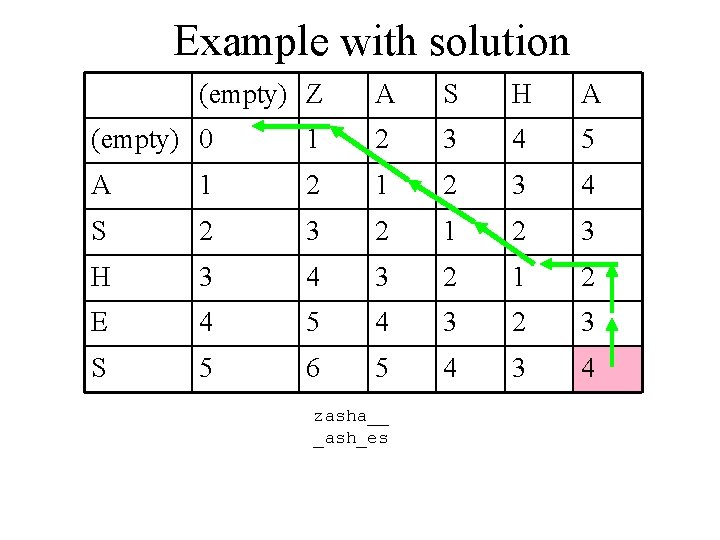
An example (empty) Z (empty) A S H E S A S H A

Example with solution (empty) Z A S H A (empty) 0 1 2 3 4 5 A 1 2 3 4 S 2 3 2 1 2 3 H 3 4 3 2 1 2 E 4 5 4 3 2 3 S 5 6 5 4 3 4 zasha__ _ash_es

Pseudocode (bottom-up) Given: Strings X, Y , Table[0. . x, 0. . y] For i=1 to x do Table[i, 0]=i For j=1 to y do Table[0, j]=i i=1, j=1 While i<=x and j<=y If X[x]=Y[y] Then // matches – no underscores Table[x, y]=Table[x-1, y-1] Else Table[x, y]=min(Table[x-1, y], Table[x, y-1])+1 End If i=i+1 If i>x Then i=1 j=j+1 End If

Pseudocode (top-down) Given: Strings X, Y , Table[0. . x, 0. . y] Best. Alignment (x, y) Compute Table[x-1, y] if necessary Compute Table[x, y-1] if necessary Compute Table[x-1, y-1] if necessary If X[x]=Y[y] Then // matches – no underscores Table[x, y]=Table[x-1, y-1] Else Table[x, y]=min(Table[x-1, y], Table[x, y-1])+1 End If

Running time • • Every square in table is filled in once Filling it in is constant time (n 2) squares alg is (n 2)

Idea of dynamic programming Albert Q. Dynamic at Whisler mountain Picture from Photo. Disc. com • Re-use expensive computations – Identify critical input to problem (e. g. best alignment of prefixes of strings) – Store results in table, indexed by critical input – Solve cells in table of other cells • Top-down often easier to program