DLD Lecture 18 Recap Recap Number SystemInterconversion Complements

DLD Lecture 18 Recap

Recap ° Number System/Inter-conversion, Complements ° Boolean Algebra ° More Logic Functions: NAND, NOR, XOR ° Minimization with Karnaugh Maps ° More Karnaugh Maps and Don’t Cares ° NAND and XOR Implementations ° Circuit Analysis and Design Procedures ° Binary Adders and Subtractors ° Magnitude Comparators and Multiplexers ° Encoders, Decoders and De. Multiplexers 2

Digital Signals ° Decimal values are difficult to represent in electrical systems. It is easier to use two voltage values than ten. ° Digital Signals have two basic states: 1 (logic “high”, or H, or “on”) 0 (logic “low”, or L, or “off”) ° Digital values are in a binary format. Binary means 2 states. ° A good example of binary is a light (only on or off) on off Power switches have labels “ 1” for on and “ 0” for off. 3

Number Systems ° Decimal is the number system that we use ° Binary is a number system that computers use ° Octal is a number system that represents groups of binary numbers (binary shorthand). It is used in digital displays, and in modern times in conjunction with file permissions under Unix systems. ° Hexadecimal (Hex) is a number system that represents groups of binary numbers (binary shorthand). Hex is primarily used in computing as the most common form of expressing a humanreadable string representation of a byte (group of 8 bits). 4
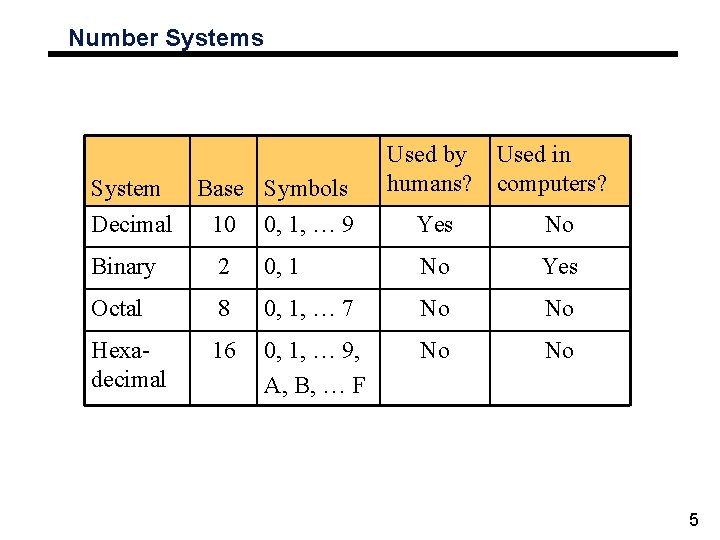
Number Systems System Base Symbols Used by humans? Used in computers? Decimal 10 0, 1, … 9 Yes No Binary 2 0, 1 No Yes Octal 8 0, 1, … 7 No No Hexadecimal 16 0, 1, … 9, A, B, … F No No 5
Conversion Among Bases The possibilities: Decimal Octal Binary Hexadecimal 6

Binary In Binary, there are only 0’s and 1’s. These numbers are called “Base-2” ( Example: 0102) Base 2 = Base 10 Binary to Decimal 000 = 0 001 = 1 010 = 2 011 = 3 100 = 4 101 = 5 110 = 6 111 = 7 We count in “Base-10” (0 to 9) ° Binary number has base 2 ° Each digit is one of two numbers: 0 and 1 ° Each digit is called a bit ° Eight binary bits make a byte ° All 256 possible values of a byte can be represented using 2 digits in hexadecimal notation. 7

Binary as a Voltage ° Voltages are used to represent logic values: ° A voltage present (called Vcc or Vdd) = 1 ° Zero Volts or ground (called gnd or Vss) = 0 A simple switch can provide a logic high or a logic low. 8
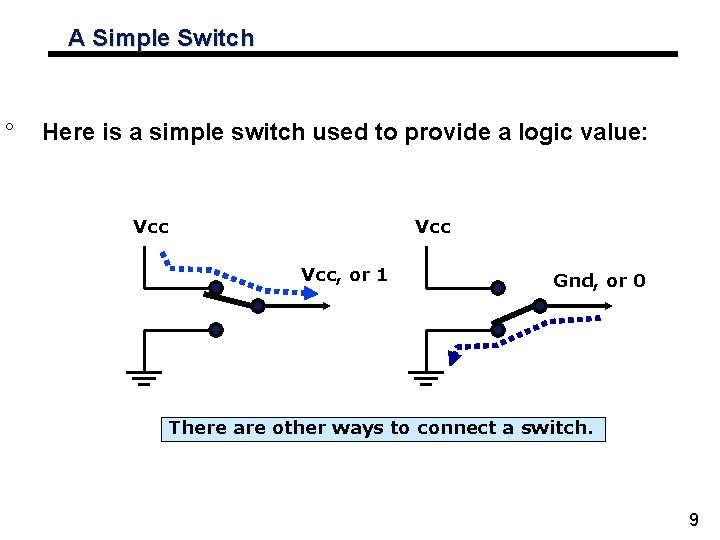
A Simple Switch ° Here is a simple switch used to provide a logic value: Vcc Vcc, or 1 Gnd, or 0 There are other ways to connect a switch. 9
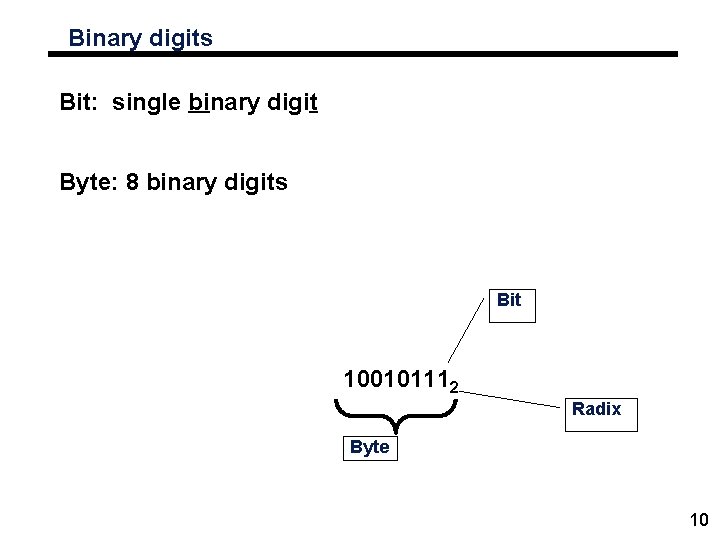
Binary digits Bit: single binary digit Byte: 8 binary digits Bit 100101112 Radix Byte 10
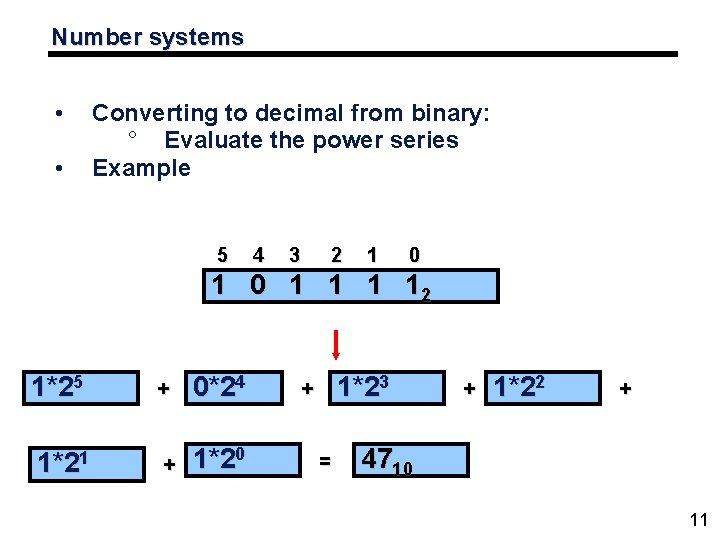
Number systems • • Converting to decimal from binary: ° Evaluate the power series Example 5 4 3 2 1 0 1 12 1*25 1*21 + 0*24 + 1*20 1*23 + = + 1*22 + 4710 11
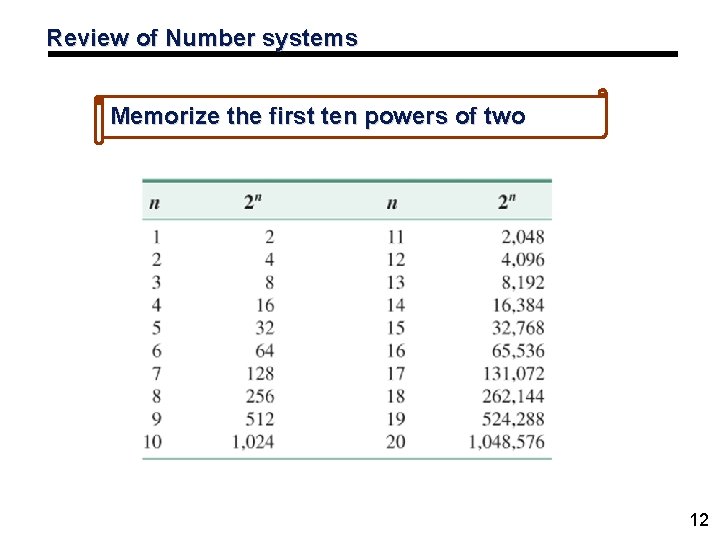
Review of Number systems Memorize the first ten powers of two 12
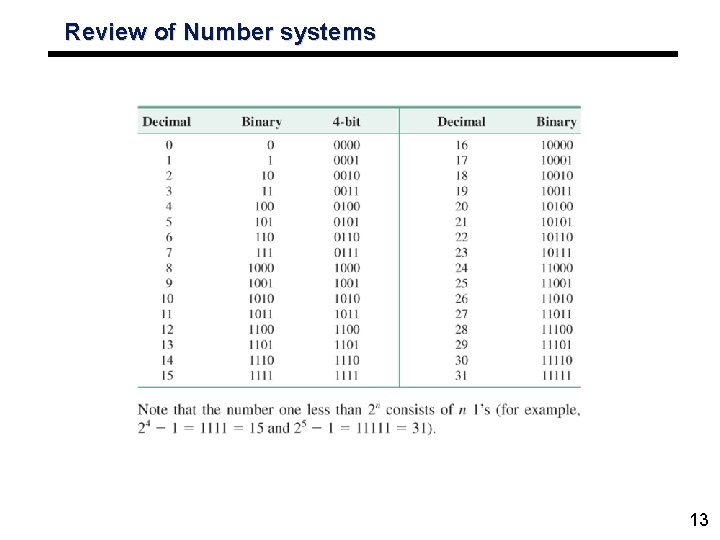
Review of Number systems 13

Number systems • Converting to binary from decimal: – Divide the decimal number by 2 repeatedly. – The remainder gives the digits of the binary number 2 2 2 2 2 746 373 R 186 R 93 R 0 1 0 46 R 23 R 11 R 1 0 1 5 R 2 R 1 R 1 1 0 10111010102 14
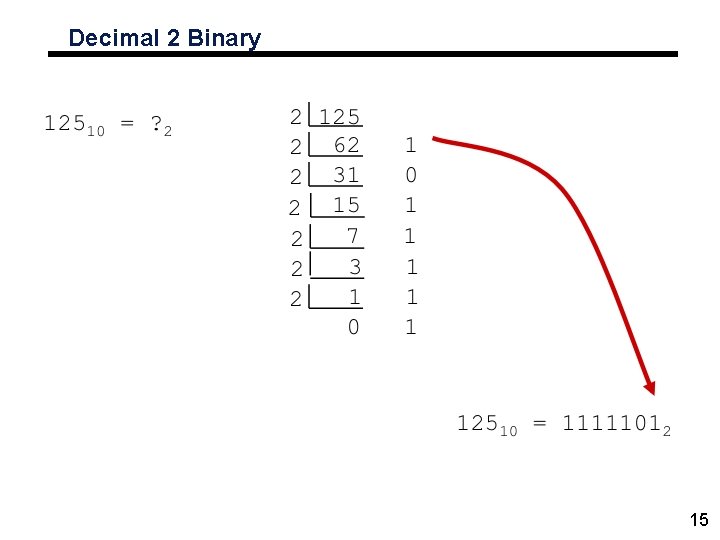
Decimal 2 Binary 15
![Number systems (Octal Numbers) ( Octal Numbers: [Base 8], [ 0, 1, 3, 4, Number systems (Octal Numbers) ( Octal Numbers: [Base 8], [ 0, 1, 3, 4,](http://slidetodoc.com/presentation_image_h2/270420fd14801fc5cca8479e6fba8942/image-16.jpg)
Number systems (Octal Numbers) ( Octal Numbers: [Base 8], [ 0, 1, 3, 4, 5, 6, 7] Octal to Decimal Conversion: Example: [2374]8 = [ ? ]10 =4× 80+7× 81+3× 82+2× 83 =[1276]10 °Octal number has base 8 °Each digit is a number from 0 to 7 °Each digit represents 3 binary bits °Was used in early computing, but was replaced by hexadecimal 16
![Number systems (Octal Numbers) ( Decimal to Octal Conversion: Quotient The Division: [359]10 = Number systems (Octal Numbers) ( Decimal to Octal Conversion: Quotient The Division: [359]10 =](http://slidetodoc.com/presentation_image_h2/270420fd14801fc5cca8479e6fba8942/image-17.jpg)
Number systems (Octal Numbers) ( Decimal to Octal Conversion: Quotient The Division: [359]10 = [ ? ]8 By using the division system: Reminder 7 4 5 5 4 7 17
![Number systems (Octal Numbers) ( Binary to Octal Conversion: Example: [110101]2 = [ ? Number systems (Octal Numbers) ( Binary to Octal Conversion: Example: [110101]2 = [ ?](http://slidetodoc.com/presentation_image_h2/270420fd14801fc5cca8479e6fba8942/image-18.jpg)
Number systems (Octal Numbers) ( Binary to Octal Conversion: Example: [110101]2 = [ ? ]8 Here we will take 3 bits and convert it from binary to decimal by using the decimal to binary truth table: Decimal 6 101 5 1 1 0 1 = (65)8 6 { 110 { Binary 5 18
![Number systems (Octal Numbers) ( Octal to Binary Conversion: Example: [13]8 = [ ? Number systems (Octal Numbers) ( Octal to Binary Conversion: Example: [13]8 = [ ?](http://slidetodoc.com/presentation_image_h2/270420fd14801fc5cca8479e6fba8942/image-19.jpg)
Number systems (Octal Numbers) ( Octal to Binary Conversion: Example: [13]8 = [ ? ]2 Here we will convert each decimal digit from decimal to binary (3 bits) using the decimal to binary truth table: Decimal Binary 1 001 3 011 (13)8 = (001011)2 19
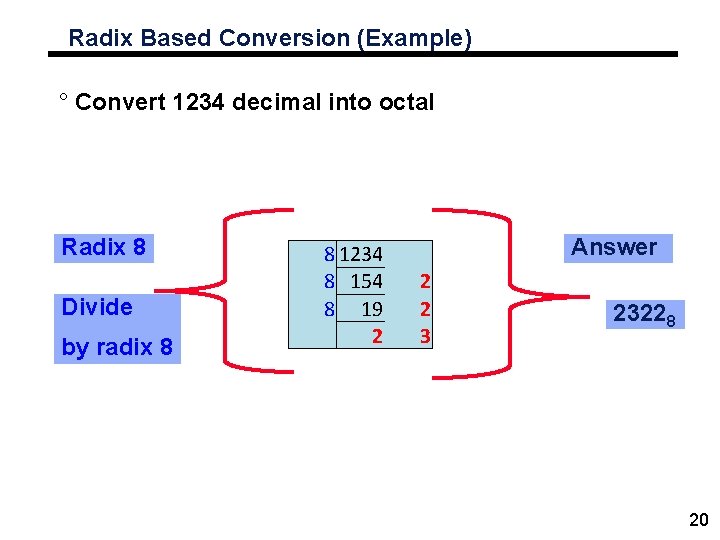
Radix Based Conversion (Example) ° Convert 1234 decimal into octal Radix 8 Divide by radix 8 8 1234 8 154 8 19 2 Answer 2 2 3 23228 20
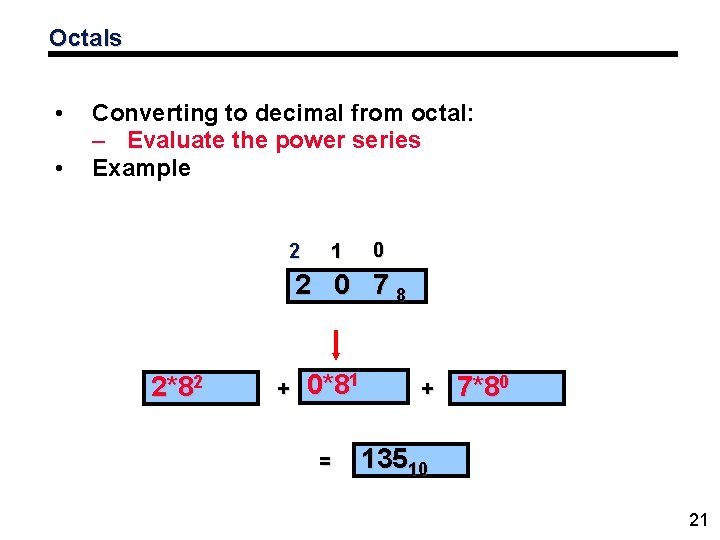
Octals • • Converting to decimal from octal: – Evaluate the power series Example 2 1 0 2 0 78 2*82 + 0*81 = + 7*80 13510 21

Hexadecimal ° Hexadecimal is used to simplify dealing with large binary values: • Base-16, or Hexadecimal, has 16 characters: 0 -9, A-F • Represent a 4 -bit binary value: 00002 (0) to 11112 (F) • Easier than using ones and zeros for large binary values • Commonly used in computer applications ° Examples: • 11002 = 1210 = C 16 • 1010 0110 1100 00102 = A 6 C 216 Hex values can be followed by an “H” to indicate base-16. Example: A 6 C 2 H 22
Hex Values in Computers 23
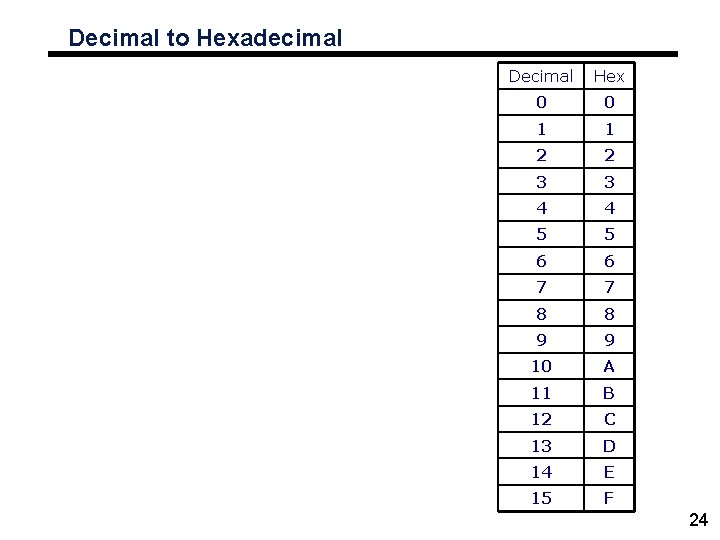
Decimal to Hexadecimal Decimal Hex 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 A 11 B 12 C 13 D 14 E 15 F 24
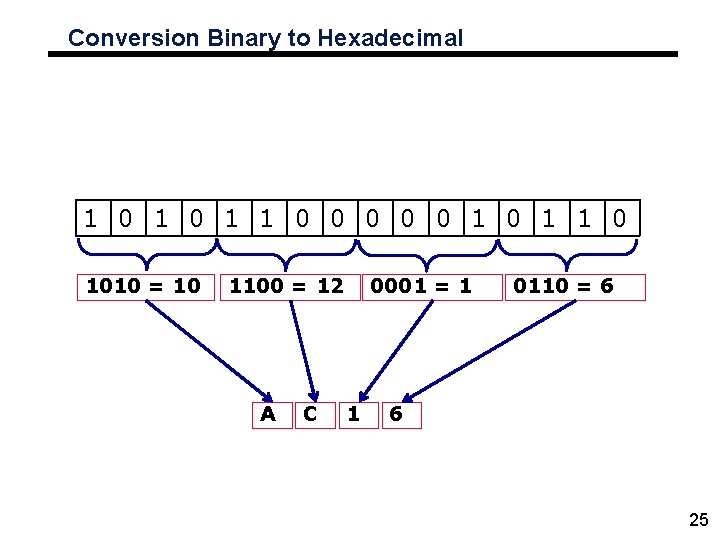
Conversion Binary to Hexadecimal 1 0 1 1 0 0 0 1 1 0 1010 = 10 1100 = 12 A C 0001 = 1 1 0110 = 6 6 25
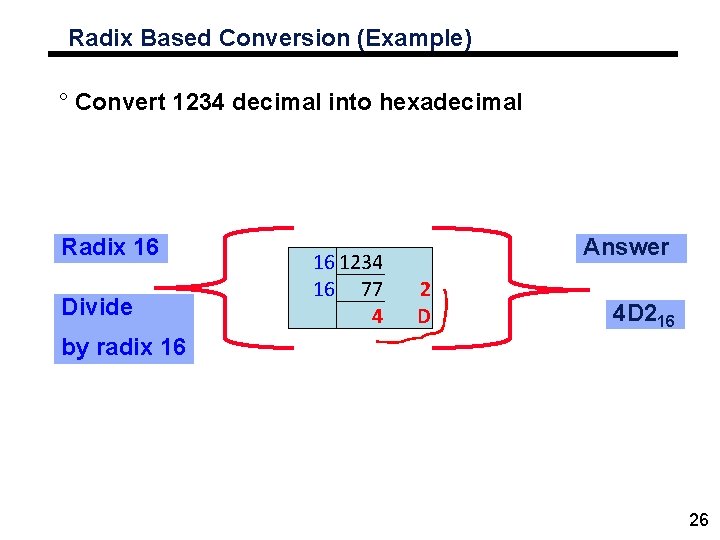
Radix Based Conversion (Example) ° Convert 1234 decimal into hexadecimal Radix 16 Divide 16 1234 16 77 4 Answer 2 D 4 D 216 by radix 16 26
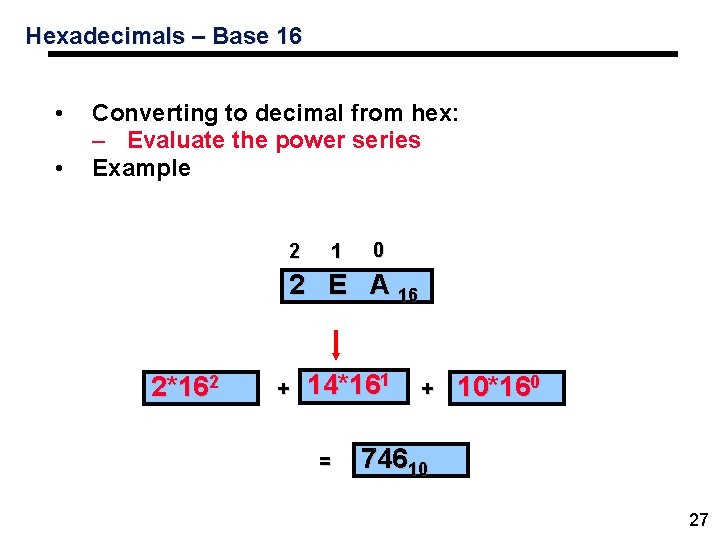
Hexadecimals – Base 16 • • Converting to decimal from hex: – Evaluate the power series Example 2 1 0 2 E A 16 2*162 + 14*161 = + 10*160 74610 27

Octal to Hex Conversion § To convert between the Octal and Hexadecimal numbering systems § Convert from one system to binary first § Then convert from binary to the new numbering system 28

Hex to Octal Conversion Ex : Convert E 8 A 16 to octal First convert the hex to binary: 1110 1000 10102 111 010 001 010 and re-group by 3 bits (starting on the right) Then convert the binary to octal: 7 2 1 2 So E 8 A 16 = 72128 29
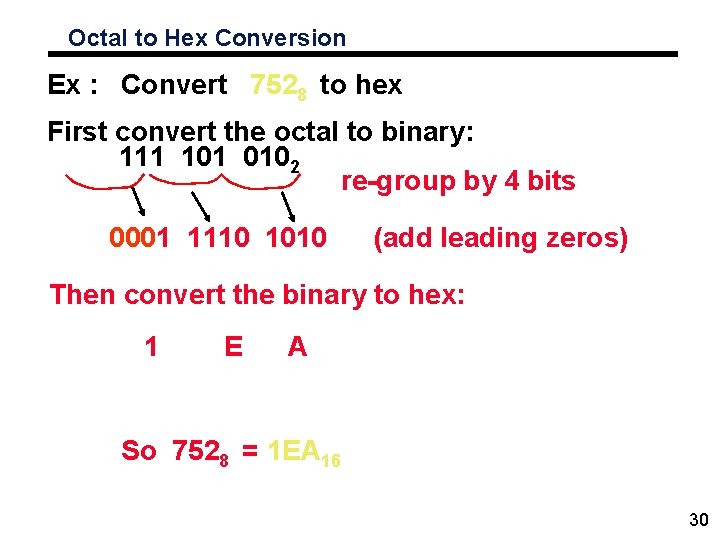
Octal to Hex Conversion Ex : Convert 7528 to hex First convert the octal to binary: 111 101 0102 re-group by 4 bits 0001 1110 1010 (add leading zeros) Then convert the binary to hex: 1 E A So 7528 = 1 EA 16 30
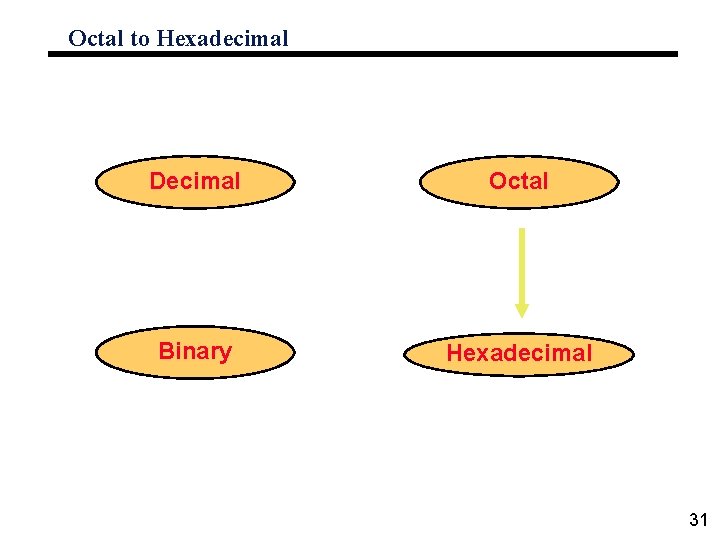
Octal to Hexadecimal Decimal Octal Binary Hexadecimal 31

Octal to Hexadecimal ° Technique • Use binary as an intermediary 32
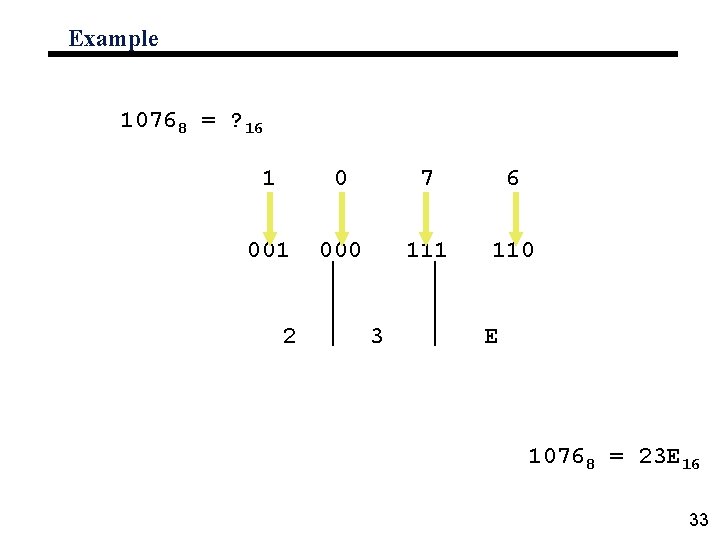
Example 10768 = ? 16 1 0 7 6 001 000 111 110 2 3 E 10768 = 23 E 16 33
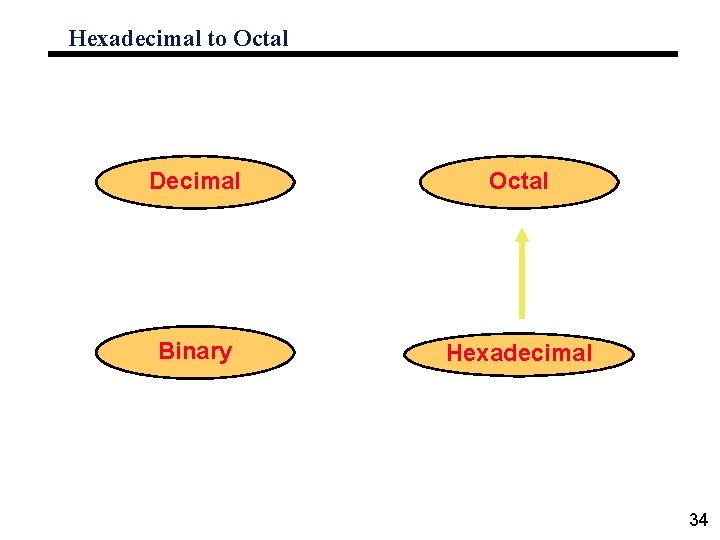
Hexadecimal to Octal Decimal Octal Binary Hexadecimal 34

Hexadecimal to Octal ° Technique • Use binary as an intermediary 35
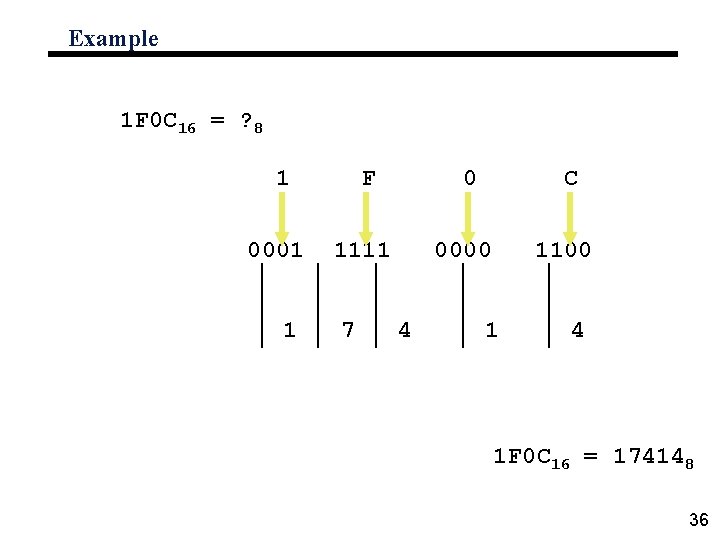
Example 1 F 0 C 16 = ? 8 1 0001 1 F 0 1111 7 C 0000 4 1100 1 4 1 F 0 C 16 = 174148 36

Example: Hex → Octal Example: ° Convert the hexadecimal number 5 AH into its octal equivalent. Solution: ° First convert the hexadecimal number into its decimal equivalent, then convert the decimal number into its octal equivalent. 5 A 161 160 16 1 80 + 10 = 9010 5 AH = 1328 37

Fractions (Example) 38

Fractions (Example) 39
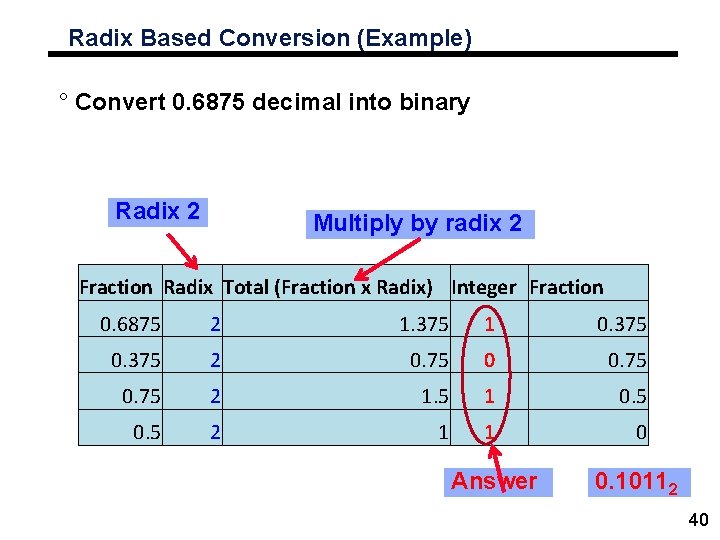
Radix Based Conversion (Example) ° Convert 0. 6875 decimal into binary Radix 2 Multiply by radix 2 Fraction Radix Total (Fraction x Radix) Integer Fraction 0. 6875 2 1. 375 1 0. 375 2 0. 75 2 1. 5 1 0. 5 2 1 1 0 Answer 0. 10112 40
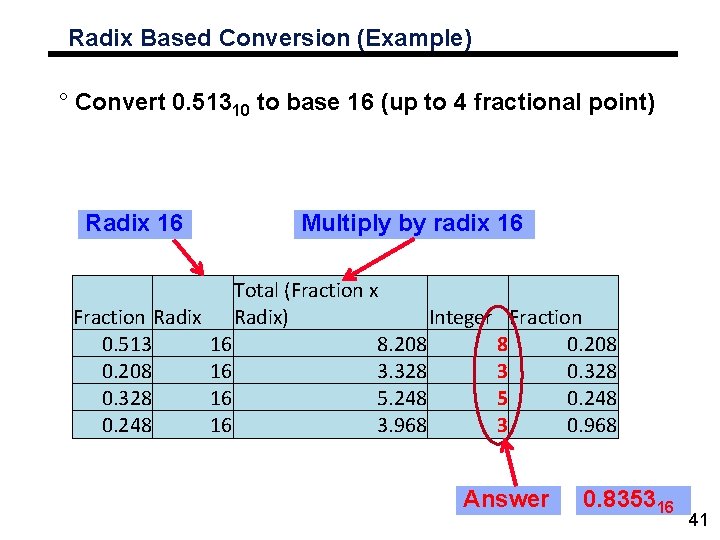
Radix Based Conversion (Example) ° Convert 0. 51310 to base 16 (up to 4 fractional point) Radix 16 Multiply by radix 16 Total (Fraction x Fraction Radix) Integer Fraction 0. 513 16 8. 208 8 0. 208 16 3. 328 3 0. 328 16 5. 248 5 0. 248 16 3. 968 3 0. 968 Answer 0. 835316 41

Any base to decimal conversion (110. 11)2 to decimal: (110. 11)2 = 6. 75. 42

43

Complement ° It has already been studied that ° subtracting one number from another is the same as making one number negative and just adding them. ° We know how to create negative numbers in the binary number system. ° How to perform 2’s complement process. ° How the 2’s complement process can be use to add (and subtract) binary numbers. ° Digital electronics requires frequent addition and subtraction of numbers. You know how to design an adder, but what about a subtracter? ° A subtracter is not needed with the 2’s complement process. The 2’s complement process allows you to easily convert a positive number into its negative equivalent. ° Since subtracting one number from another is the same as making one number negative and adding, the need for a 44 subtracter circuit has been eliminated.
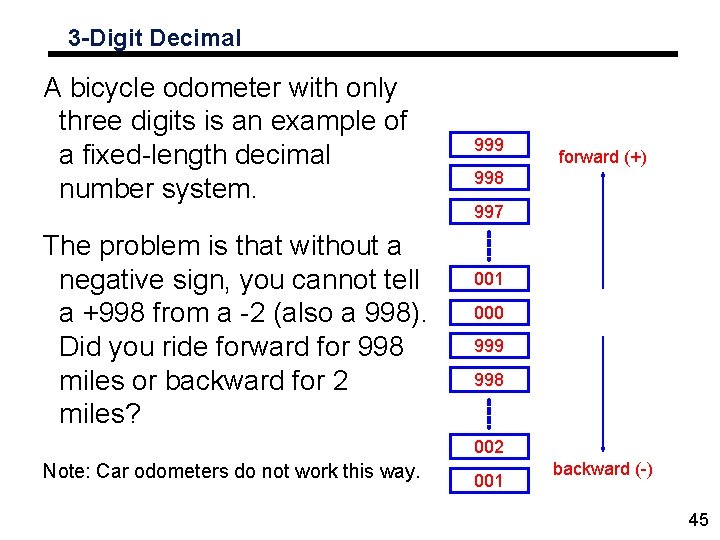
3 -Digit Decimal A bicycle odometer with only three digits is an example of a fixed-length decimal number system. The problem is that without a negative sign, you cannot tell a +998 from a -2 (also a 998). Did you ride forward for 998 miles or backward for 2 miles? 999 forward (+) 998 997 001 000 999 998 002 Note: Car odometers do not work this way. 001 backward (-) 45

Negative Decimal How do we represent negative numbers in this 3 digit decimal number system without using a sign? +499 +498 +497 Cut the number system in half. +001 Use 001 – 499 to indicate positive numbers. 000 -001 999 -002 998 -499 501 -500 Use 500 – 999 to indicate negative numbers. Notice that 000 is not positive or negative. pos(+) neg(-) 46

3 -Digit Decimal (Examples) 3 + 2 5 003 + 002 005 6 + (-3) 006 + 997 3 1 003 Disregard Overflow (-5) + 2 995 + 002 (-2) + (-3) 998 + 997 (-3) 997 (-5) 1 995 It Works! Disregard Overflow 47

Complex Problem ° The previous examples demonstrate that this process works, but how do we easily convert a number into its negative equivalent? ° In the examples, converting the negative numbers into the 3 -digit decimal number system was fairly easy. To convert the (-3), you simply counted backward from 1000 (i. e. , 999, 998, 997). ° This process is not as easy for large numbers (e. g. , -214 is 786). How did we determine this? ° To convert a large negative number, you can use the 10’s Complement Process. 48

The 10’s Complement process uses base-10 (decimal) numbers. Later, when we’re working with base-2 (binary) numbers, you will see that the 2’s Complement process works in the same way. First, complement all of the digits in a number. • A digit’s complement is the number you add to the digit to make it equal to the largest digit in the base (i. e. , 9 for decimal). The complement of 0 is 9, 1 is 8, 2 is 7, etc. Second, add 1. • Without this step, our number system would have two zeroes (+0 & -0), which no number system has. 49

10’s Complement Examples Example #1 -003 996 +1 997 Complement Digits Add 1 Example #2 -214 785 +1 786 Complement Digits Add 1 50

8 -Bit Binary Number System Apply what you have learned to the binary number systems. How do you represent negative numbers in this 8 bit binary system? Cut the number system in half. Use 00000001 – 01111111 to indicate positive numbers. Use 10000000 – 1111 to indicate negative numbers. Notice that 0000 is not positive or negative. +127 01111111 +126 01111110 +125 01111101 +1 00000001 0 0000 -1 1111 -2 11111110 -127 10000001 -128 10000000 51 51

Sign Bit • • • What did do you notice about the most significant bit of the binary numbers? The MSB is (0) for all positive numbers. +127 01111111 +126 01111110 +125 01111101 +1 00000001 The MSB is (1) for all negative numbers. 0 0000 -1 1111 • The MSB is called the sign bit. -2 11111110 • In a signed number system, this allows you to instantly determine whether a number is positive or negative. -127 10000001 -128 10000000 pos(+) neg(-) 52

2’S Complement Process The steps in the 2’s Complement process are similar to the 10’s Complement process. However, you will now use the base two. First, complement all of the digits in a number. • A digit’s complement is the number you add to the digit to make it equal to the largest digit in the base (i. e. , 1 for binary). In binary language, the complement of 0 is 1, and the complement of 1 is 0. Second, add 1. • Without this step, our number system would have two zeroes (+0 & -0), which no number system has. 53

2’s Complement Examples Example #1 5 = 00000101 11111010 +1 -5 = 11111011 Complement Digits Add 1 Example #2 -13 = 11110011 00001100 +1 13 = 00001101 Complement Digits Add 1 54

Using The 2’s Compliment Process Use the 2’s complement process to add together the following numbers. POS + POS 9 + 5 14 NEG + POS NEG POS + NEG POS 9 + (-5) 4 NEG + NEG (-9) + (-5) - 14 (-9) + 5 -4 55

POS + POS → POS Answer If no 2’s complement is needed, use regular binary addition. 9 + 5 14 00001001 + 00000101 00001110 56

POS + NEG → POS Answer Take the 2’s complement of the negative number and use regular binary addition. 9 + (-5) 4 00001001 + 11111011 1]00000100 8 th Bit = 0: Answer is Positive Disregard 9 th Bit 00000101 11111010 +1 11111011 2’s Complement Process 57

POS + NEG → NEG Answer Take the 2’s complement of the negative number and use regular binary addition. (-9) + 5 -4 11110111 + 00000101 11111100 8 th Bit = 1: Answer is Negative To Check: Perform 2’s Complement On Answer 11111100 00000011 +1 000001001 11110110 +1 11110111 2’s Complement Process 58

NEG + NEG → NEG Answer Take the 2’s complement of both negative numbers and use regular binary addition. (-9) + (-5) -14 11110111 + 11111011 1]11110010 2’s Complement Numbers, See Conversion Process In Previous Slides 8 th Bit = 1: Answer is Negative Disregard 9 th Bit To Check: Perform 2’s Complement On Answer 11110010 00001101 +1 00001110 59
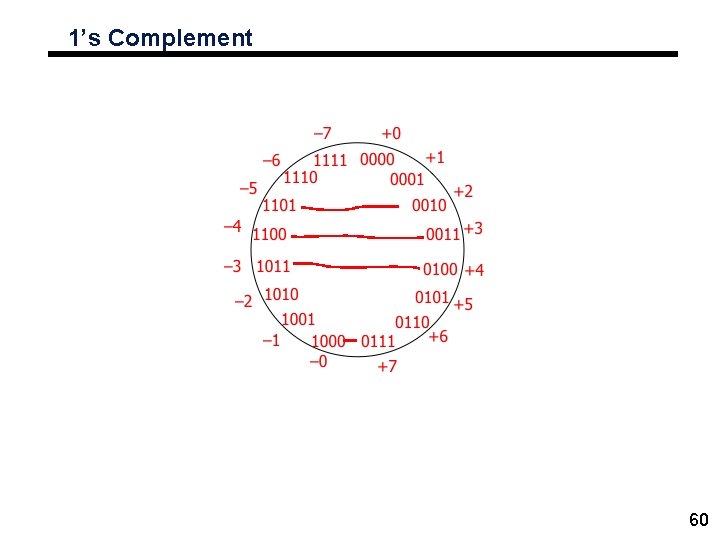
1’s Complement 60

2’s Complement • 1 s complement with negative numbers shifted one position clockwise • Only one representation for 0 • One more negative number than positive number • High-order bit can act as sign bit 61

Overflow ° Overflow conditions ° Add two positive numbers to get a negative number ° Add two negative numbers to get a positive number 62
- Slides: 62