Dividing Polynomials Lesson 6 3 Algebra 2 Additional

Dividing Polynomials Lesson 6 -3 Algebra 2 Additional Examples Divide x 2 + 2 x – 30 by x – 5. x x – 5 x 2 + 2 x – 30 x 2 – 5 x 7 x – 30 Bring down – 30. x 2 Divide = x. x Multiply: x(x – 5) = x 2 – 5 x Subtract: (x 2 + 2 x) – (x 2 – 5 x) = 7 x. Repeat the process of dividing, multiplying, and subtracting. x + 7 x – 5 x 2 + 2 x – 30 x 2 – 5 x 7 x – 30 7 x – 35 5 7 x x Divide = 7. Multiply: 7(x – 5) = 7 x – 35. Subtract: (7 x – 30) – (7 x – 35) = 5. The quotient is x + 7 with a remainder of 5, or simply x + 7, R 5.

Dividing Polynomials Lesson 6 -3 Algebra 2 Additional Examples Determine whether x + 2 is a factor of each polynomial. a. x 2 + 10 x + 16 x + 8 x + 2 x 2 + 10 x + 16 x 2 + 2 x 8 x + 16 0 Since the remainder is zero, x + 2 is a factor of x 2 + 10 x + 16. b. x 3 + 7 x 2 – 5 x – 6 x 2 + 5 x – 15 x + 2 x 3 + 7 x 2 – 5 x – 6 x 3 + 2 x 2 5 x 2 – 5 x 5 x 2 + 10 x – 15 x – 6 – 15 x – 30 24 Since the remainder = 0, x + 2 is / not a factor of x 3 + 7 x 2 – 5 x – 6.

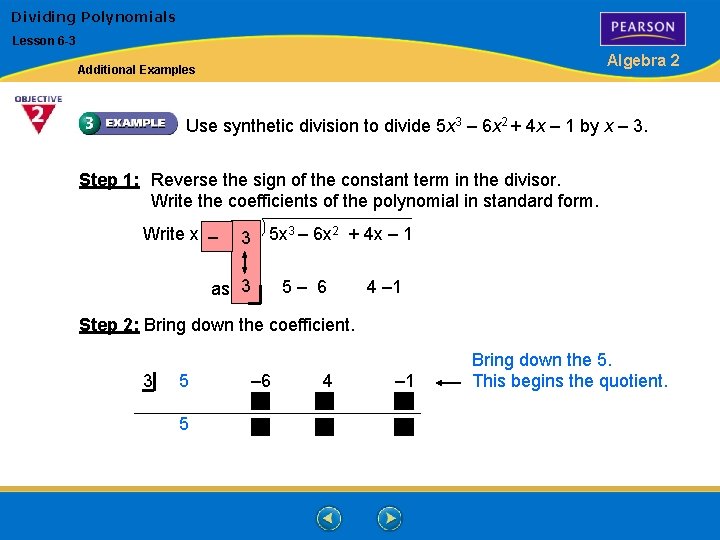
Dividing Polynomials Lesson 6 -3 Algebra 2 Additional Examples Use synthetic division to divide 5 x 3 – 6 x 2 + 4 x – 1 by x – 3. Step 1: Reverse the sign of the constant term in the divisor. Write the coefficients of the polynomial in standard form. 3 – 6 x 2 + 4 x – 1 Write x 5 x – 3 as 3 5 – 6 4 – 1 Step 2: Bring down the coefficient. 3 5 5 – 6 4 – 1 Bring down the 5. This begins the quotient.

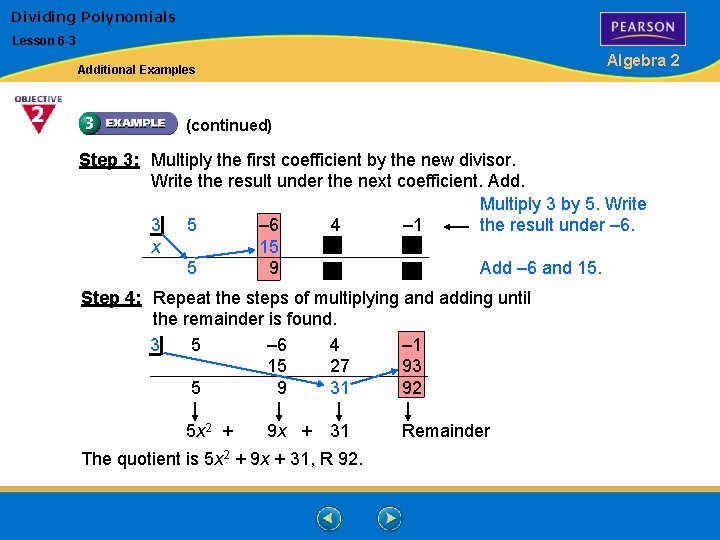
Dividing Polynomials Lesson 6 -3 Algebra 2 Additional Examples (continued) Step 3: Multiply the first coefficient by the new divisor. Write the result under the next coefficient. Add. Multiply 3 by 5. Write 3 5 – 6 4 – 1 the result under – 6. x 15 5 9 Add – 6 and 15. Step 4: Repeat the steps of multiplying and adding until the remainder is found. 3 5 – 6 4 – 1 15 27 93 5 9 31 92 5 x 2 + 9 x + 31 The quotient is 5 x 2 + 9 x + 31, R 92. Remainder

Dividing Polynomials Lesson 6 -3 Additional Examples Algebra 2 The volume in cubic feet of a shipping carton is V(x) = x 3 – 6 x 2 + 3 x + 10. The height is x – 5 feet. a. Find linear expressions for the other dimensions. Assume that the length is greater than the width. 5 1 – 6 3 10 Divide. 5 – 10 1 – 2 0 x 2 – x – 2 Remainder x 2 – x – 2 = (x – 2)(x + 1) Factor the quotient. The length and the width are x + 1 and x – 2, respectively. b. If the width of the carton is 4 feet, what are the other two dimensions? x – 2 = 4 Substitute 4 into the expression for width. Find x. x = 6 Since the height equals x – 5 and the length equals x + 1, the height is 1 ft. and the length is 7 ft.

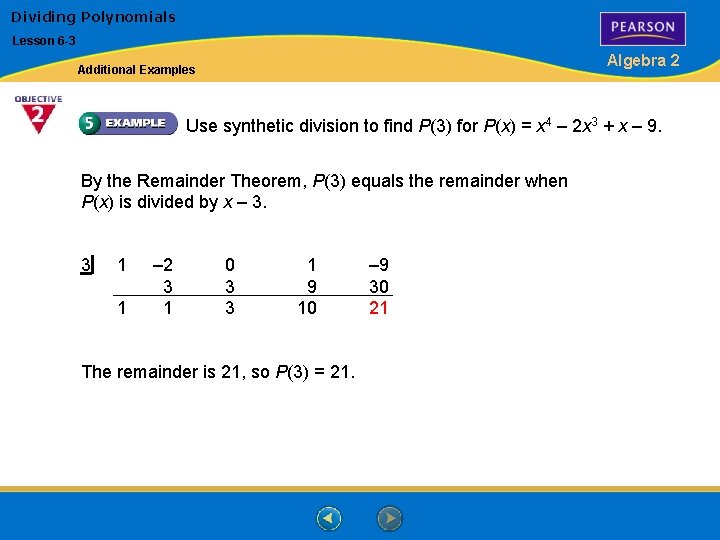
Dividing Polynomials Lesson 6 -3 Algebra 2 Additional Examples Use synthetic division to find P(3) for P(x) = x 4 – 2 x 3 + x – 9. By the Remainder Theorem, P(3) equals the remainder when P(x) is divided by x – 3. 3 1 1 – 2 3 1 0 3 3 1 9 10 The remainder is 21, so P(3) = 21. – 9 30 21