Dividend Policy and Dividend Payment Behavior Theory and

Dividend Policy and Dividend Payment Behavior: Theory and Evidence* Cheng-Few Lee (lee@business. rutgers. edu) Distinguished Professor of Finance, Rutgers University Visiting Chair Professor, NCTU, Taiwan Editor of RQFA and RPBFMP *Keynote Speech delivered at International Academy of Information Technology and Quantitative Management (IAITQM), Suzhou, China, May 16 May 18, 2013

Outline I. Flow Chart of Dividend Policy and Dividend Behavior a) b) c) d) Theory Dividend Behavior Models Price dividend Multiplier Model Integration of Dividend Policy and CAPM II. Optimal Payout Ratio Under Uncertainty and The Flexibility Hypothesis: Theory and Empirical Evidence (Lee et al. 2011, JCF) a) b) c) d) e) f) g) I. Introduction Review of the literature The model Optimum dividend policy Relationship between the optimal payout ratio and the growth rate Relationship between optional payout ratio and risks Empirical evidence Sustainable growth rate, optimal growth rate, and optimal payout ratio: A joint optimization approach (Chen et al. 2013, JBF) a) b) c) I. Introduction The model Stochastic growth rate and specification error on expected dividend Empirical evidence 2

Outline IV. Current vs. Permanent Earnings for Estimating Alternative Dividend Payment Behavioral Model: Theory, Methods and Applications(Lee et al. 2013) a) Introduction b) Theoretical determination of firm’s permanent and transitory earnings c) d) and dividends Alternative methods for decomposing current EPS into permanent and transitory EPS components 1. 2. 3. 4. Darby’s (1974) method Lee and Primeaux’s (1991) method Garrett and Priestley’s (2000) Kalman filter method Lambrecht and Myer’s (2012) method 1. 2. 3. Darby’s method and Lee and Primeaux’s method Lambrecht and Myer’s method Combined model Empirical results in estimating two alternative dividend behavior models V. Concluding Remarks and Future Research IV. V. VI. a) Conclusion for paper 1 Conclusion for paper 2 Conclusion for paper 3 Dividend policy, dividend payment behavior, and price dividend multiplier are interrelated. 3
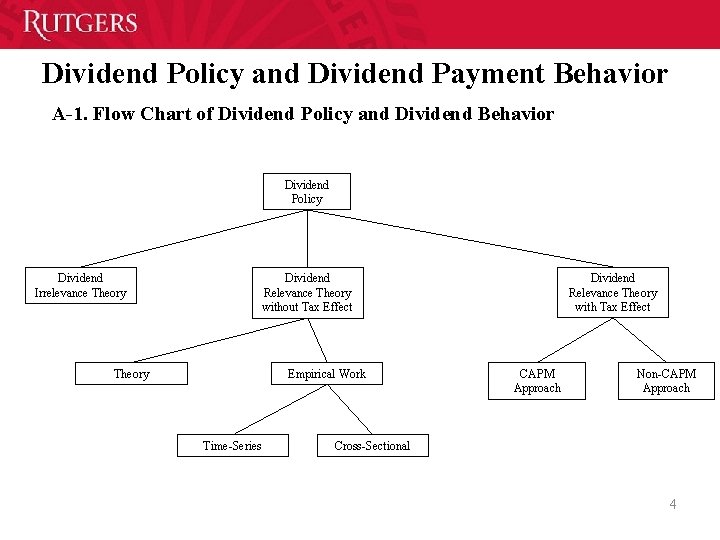
Dividend Policy and Dividend Payment Behavior A-1. Flow Chart of Dividend Policy and Dividend Behavior Dividend Policy Dividend Irrelevance Theory Dividend Relevance Theory without Tax Effect Empirical Work Theory Time Series Dividend Relevance Theory with Tax Effect CAPM Approach Non CAPM Approach Cross Sectional 4
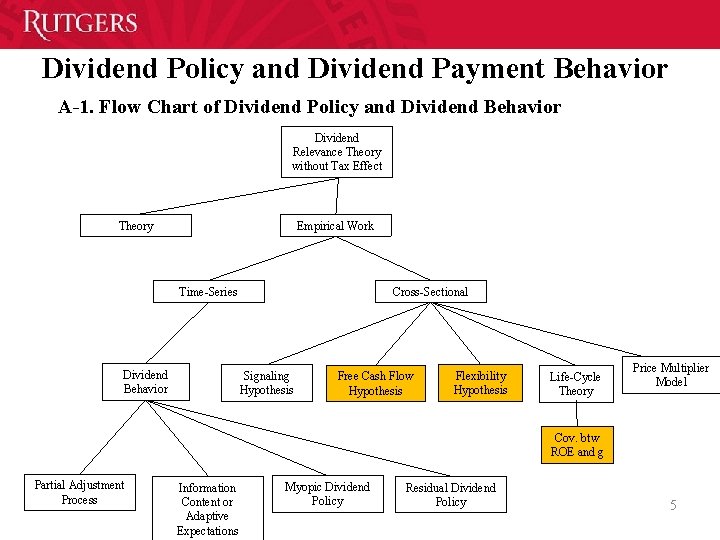
Dividend Policy and Dividend Payment Behavior A-1. Flow Chart of Dividend Policy and Dividend Behavior Dividend Relevance Theory without Tax Effect Theory Empirical Work Time Series Dividend Behavior Cross Sectional Signaling Hypothesis Free Cash Flow Hypothesis Flexibility Hypothesis Life Cycle Theory Price Multiplier Model Cov. btw ROE and g Partial Adjustment Process Information Content or Adaptive Expectations Myopic Dividend Policy Residual Dividend Policy 5
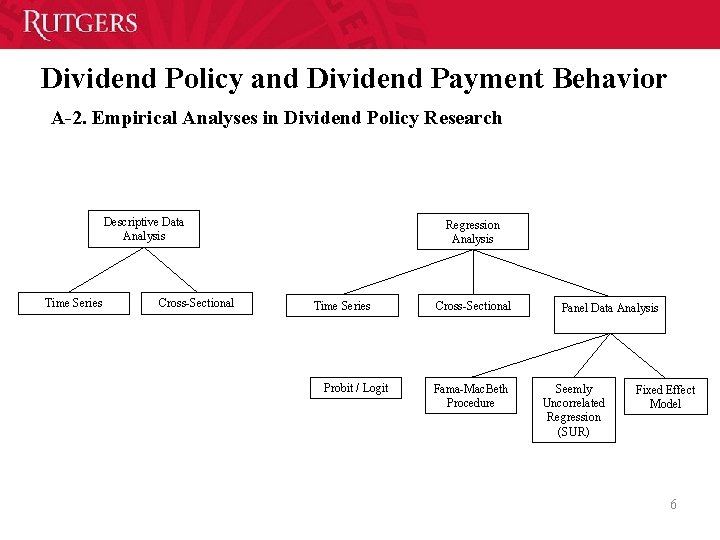
Dividend Policy and Dividend Payment Behavior A-2. Empirical Analyses in Dividend Policy Research Descriptive Data Analysis Time Series Cross Sectional Regression Analysis Time Series Probit / Logit Cross Sectional Fama Mac. Beth Procedure Panel Data Analysis Seemly Uncorrelated Regression (SUR) Fixed Effect Model 6
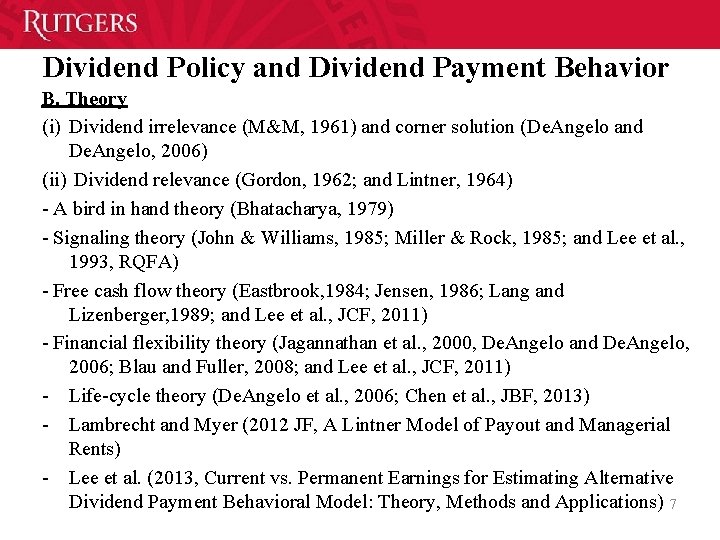
Dividend Policy and Dividend Payment Behavior B. Theory (i) Dividend irrelevance (M&M, 1961) and corner solution (De. Angelo and De. Angelo, 2006) (ii) Dividend relevance (Gordon, 1962; and Lintner, 1964) A bird in hand theory (Bhatacharya, 1979) Signaling theory (John & Williams, 1985; Miller & Rock, 1985; and Lee et al. , 1993, RQFA) Free cash flow theory (Eastbrook, 1984; Jensen, 1986; Lang and Lizenberger, 1989; and Lee et al. , JCF, 2011) Financial flexibility theory (Jagannathan et al. , 2000, De. Angelo and De. Angelo, 2006; Blau and Fuller, 2008; and Lee et al. , JCF, 2011) Life cycle theory (De. Angelo et al. , 2006; Chen et al. , JBF, 2013) Lambrecht and Myer (2012 JF, A Lintner Model of Payout and Managerial Rents) Lee et al. (2013, Current vs. Permanent Earnings for Estimating Alternative Dividend Payment Behavioral Model: Theory, Methods and Applications) 7

Dividend Policy and Dividend Payment Behavior C. Dividend Behavior Models (i) Partial Adjustment Model (Lintner, 1956 AER) Current earnings => Lintner’s model Permanent earnings => Lee and Primeaux (1991) and Lambrecht and Myers (2012) (ii) Mixed Partial Adjustment and Adapted Expectation (Fama & Babiak, 1968 JASA) (iii) Generalized Dividend Forecasting Model (Lee et al. , 1987, Journal of Econometrics) 8

Dividend Policy and Dividend Payment Behavior D. Price-Dividend Multiplier Model (i) Friend and Puckett (1964, AER) have proposed the relationship between stock prices, dividends, and retained earnings as follows: where Based upon Eq. (1) and discount cash flow model in terms of optimal forecasting, Granger (1975 JF) has shown that B and C can be written in terms of discount rate, , and of Eq. (1). Therefore, it can be concluded that Eq. (3) is a theoretical derived model instead of an ad hoc model. (ii) Lee (1976, JF), Chang and Lee (1977, JFQA), and Gilmore and Lee (1986, RES) have done empirical studies on price multiplier model. 9

Dividend Policy and Dividend Payment Behavior E. Integration of Dividend Policy and CAPM (Litzenberger and Ramaswamy, 1982) A is the excess return on a zero beta portfolio with a dividend yield equal to the riskless rate of interest, relative to the market portfolio. B is similar to the market risk premium concept in the original CAPM. C represents a balancing of risks. The further discussion of Eq. (4) can be found in Litzenberger and Ramaswamy (1982) or Lee et al. (2009). 10

Optimal Payout Ratio Under Uncertainty and The Flexibility Hypothesis: Theory and Empirical Evidence (Lee et al. 2011, JCF) Introduction Dividend Policy Miller and Modigliani (1961) Firm Value is independent of dividend policy. Assumptions of M&M theory 1) no tax. 2) no capital market frictions (i. e. , no transaction cost, asset trade restriction, or bankruptcy cost) 3) firms and investors can borrow or lend at the same rate. 4) firm financial policy reveals no information. 5) only consider no payout and payout all free cash flow. De. Angelo and De. Angelo (2006) > M&M (1961) irrelevance result is “irrelevant” because it only considers payout policies that pay out all free cash flow. > Payout policy matters when partial payouts are allowed. 11

Introduction • • • Signaling Hypothesis The signaling hypothesis suggests managers with better information than the market will signal this private information using dividends. A company announcements of an increase in dividend payouts act as an indicator of the firm possessing strong future prospects. [Bhatacharya (1979), John and Williams (1985), Miller and Rock (1985), and Nissam and Ziv (2001)] Free Cash Flow Hypothesis (Agency Cost) Dividend payment can reduce potential agency problem. [Eastbrook (1984), Jensen (1986), Lang and Lizenberger(1989), Lie (2000), and Grullon et al. (2002)] Financial Flexibility Management trades off two aspects of Dividends. One is financial flexibility by not paying dividends. Another is deterioration on stock price if not paying dividends. 12 [Blau and Fuller (2008)]

Introduction 1. Based on the De. Angelo & De. Angelo (2006) static analysis, we derive a theoratical dynamic model and show that there exists an optimal payout ratio under perfect market. 2. We derive the relationship between firm’s optimal payout ratio and its risks. 3. We derive the relationship between firm’s optimal payout ratio and its growth. 4. We further develop a fully dynamic model for determining the time optimal growth and dividend policy under the imperfect market, the uncertainty of the investment, and the dynamic growth rate. 5. We study the effects of the time varying horizons, the degree of market perfection, and stochastic initial conditions in determining an optimal growth and dividend policy for the firm. 6. When the stochastic growth rate is introduced, the expected return may suffer a model specification. 7. Empirical evidence of the determination of the optimal payout policy. 13

The Model for Optimal Dividend Policy Let represent the initial assets of the firm and represent the growth rate. Then, the earnings of this firm are given by Eq. (1), which is The retained earnings of the firm, where , can be expressed as is the number of shares outstanding, and is dividend per share at time t. 14

The Model for Optimal Dividend Policy The new equity raised by the firm at time t can be defined as where = degree of market perfection, 0 < 1. Therefore, the investment in period t can be written as: Rearranging the equation above, we can get 15

The Model for Optimal Dividend Policy The stock price should equal the present value of this certainty equivalent dividend stream discounted at the cost of capital (k) of the firm. A differential equation can be formulated: where 16

Optimal Dividend Policy Optimal Payout Ratio when : 17

Relationship between the Optimal Payout Ratio and the Growth Rate The sign is not only affected by the growth rate (h), but is also affected by the expected rate of return on assets ( ), the duration of future dividend payments (T-t), and the cost of capital (k). Sensitivity analysis shows that the relationship between the optimal payout ratio and the growth rate is generally negative. =>a firm with a higher rate of return on assets tends to payout less when its growth opportunities increase. 18

19

Relationship between the Optimal Payout Ratio and the Growth Rate When , there is a negative relationship between the optimal payout ratio and the growth rate. =>when a firm with a high growth rate or a low rate of return on assets faces a growth opportunity, it will decrease its dividend payout to generate more cash to meet such a new investment. 20

Implications Hypothesis 1: firms generally reduce their dividend payouts when their growth rates increase. The negative relationship between the payout ratio and the growth ratio in our theoretical model implies that high growth firms need to reduce the payout ratio and retain more earnings to build up “precautionary reserves, ” while low growth firms are likely to be more mature and already build up their reserves for flexibility concerns. [Rozeff (1982), Fama and French (2001), Blau and Fuller (2008), etc. ] 21

Optimal Payout Ratio vs. Total Risk Þ High growth firms : negative relationship between optimal payout ratio and total risk. Þ Low growth firms : positive relationship between optimal payout ratio and total risk 22

Optimal Payout Ratio vs. Systematic Risk Þ High growth firms : negative relationship between optimal payout ratio and systematic risk. Þ Low growth firms : positive relationship between optimal payout ratio and systematic risk 23

Implications • Hypothesis 2: the relationship between the firms’ dividend payouts and their risks is negative when their growth rates are higher than their rates of return on asset. Flexibility Hypothesis High growth firms need to reduce the payout ratio and retain more earnings to build up “precautionary reserves. ” These reserves become more important for a firm with volatile earnings over time. => For flexibility concerns, high growth firms tend to retain more earnings when they face higher risk. 24

Implications • Hypothesis 3: the relationship between the firms’ dividend payouts and their risks is positive when their growth rates are lower than their rates of return on asset. Free Cash Flow Hypothesis 1. Low growth firms are likely to be more mature and most likely already built such reserves over time. 2. They probably do not need more earnings to maintain their low growth perspective and can afford to increase the payout [see Grullon et al. (2002)]. 3. The higher risk may involve higher cost of capital and make free cash flow problem worse for low growth firms. => For free cash flow concerns, low growth firms tend to pay more dividends when they face higher risk 25

Optimal Payout Ratio vs. Total Risk and Systematic Risk where • Relative effect on the optimal dividend payout ratio 26

Optimal Payout Ratio when No Change in Risk When there is no change in risk, the optimal payout ratio is identical to the optimal payout ratio of Wallingford (1972). 27

Joint Optimization of Growth Rate and Payout Ratio (Chen et al. 2013 JBF) • The new investment at time t is Retained Earnings New Equity New Debt where 28

Joint Optimization of Growth Rate and Payout Ratio • The model defined in previous slide is for the convenience purpose. If we want the company’s leverage ratio unchanged after the expansion of assets then we need to modify the equation as we can obtain the growth rate as Our Model Higgins’ sustainable g which is the generalized version of Higgins’ (1977) sustainable growth rate model. Our model shows that Higgins’ (1977) sustainable growth rate is under estimated due to the omission of the source of the growth related to new equity issue which is the second term of our model. 29

Joint Optimization of Growth Rate and Payout Ratio Discount cash flow The price per share can be expressed as PV of future dividends with a risk adjustment. Future Dividends Risk Adj. => maximize p(o) by jointly determine g(t) and n(t). 30

Optimal Growth Rate Logistic Equation – Verhulst (1845) => a convergence process 31

Case I: Optimal Growth Rate v. s. Time Horizon 32
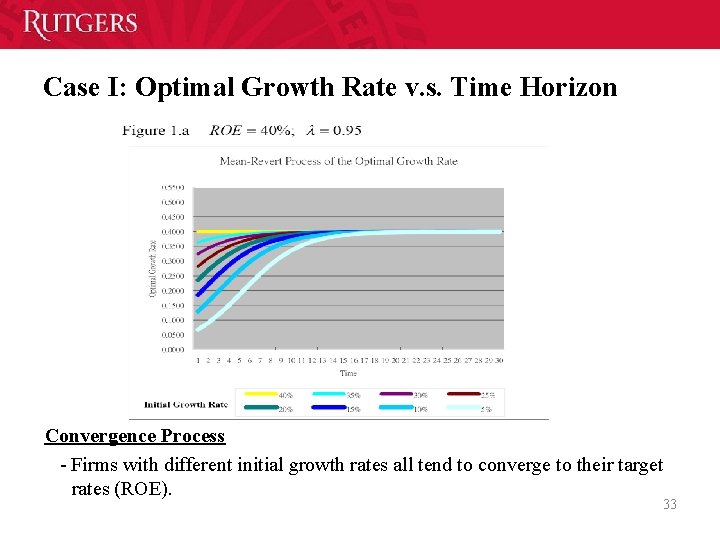
Case I: Optimal Growth Rate v. s. Time Horizon Convergence Process Firms with different initial growth rates all tend to converge to their target rates (ROE). 33

Case II: Optimal Growth Rate v. s. Degree of Market Perfection 34
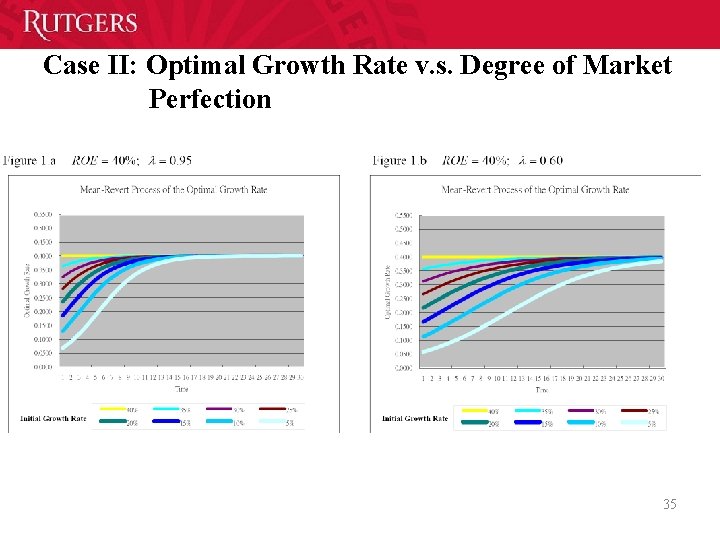
Case II: Optimal Growth Rate v. s. Degree of Market Perfection 35

Case III: Optimal Growth Rate v. s. ROE When initial growth rate is lower than the target rate (ROE), positive. is => If the target rate (ROE) is higher, the adjustment process will be faster. 36

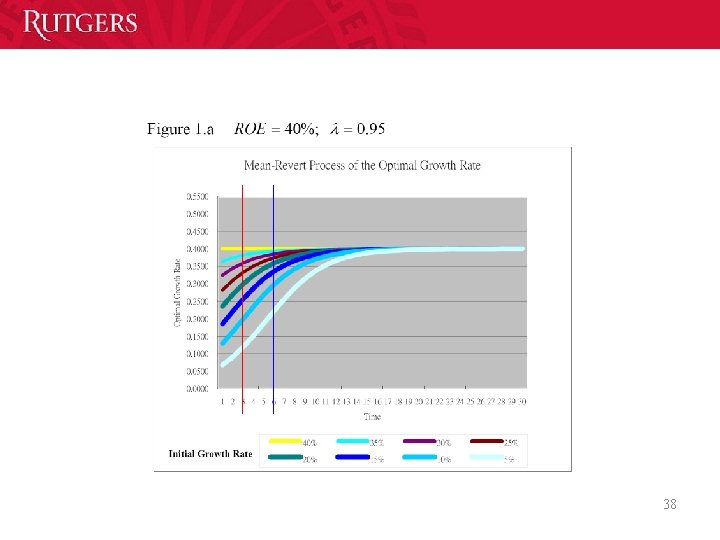
Case IV: Optimal Growth Rate v. s. Initial Growth Rate is always positive. => The higher initial growth rate is, the higher optimal growth rate at each time. 37
38

Optimal Dividend Payout Ratio where • Assuming , Wallingford (1972), Lee et al. (2010) 39

Optimal Dividend Payout Ratio v. s. Growth Rate The relationship between optimal dividend payout and growth rate is negative in general cases. 40

Stochastic Growth Rate and Specification Error Retained Earnings New Equity New Debt When a stochastic growth rate is introduced, 41

Stochastic Growth Rate and Specification Error 42

Hypotheses Development • Hypothesis 1: The firm’s growth rate follows a mean-reverting process. H 1 a: There exists a target rate of the firm’s growth rate, and the target rate is the firm’s return on equity. H 1 b: The firm partially adjusts its growth rate to the target rate. H 1 c: The partial adjustment is fast in the early stage of the mean-reverting process. • Hypothesis 2: The firm’s dividend payout is negatively associated with the covariance between the firm’s rate of return on equity and the firm’s growth rate. H 2 a: The covariance between the firm’s rate of return on equity and the firm’s growth rate is one of the key determinants of the dividend payout policy. 43

Hypotheses Development • Hypothesis 3: The firm tends to pay a dividend if its covariance between the firm’s rate of return on equity and the firm’s growth rate is lower. H 3 a: The firm tends to stop paying a dividend if its covariance between the firm’s rate of return on equity and the firm’s growth rate is higher. H 3 b: The firm tends to start paying a dividend if its covariance between the firm’s rate of return on equity and the firm’s growth rate is lower. 44

Sample • Stock price, stock returns, share codes, and exchange codes are CRPS. Firm information, such as total asset, sales, net income, and dividends payout , etc. , is collected from COMPUSTAT. • The sample period is from 1969 to 2008. • Only common stocks (SHRCD = 10, 11) and firms listed in NYSE, AMEX, or NASDAQ (EXCE = 1, 2, 3, 31, 32, 33) are included. • Utility firms and financial institutions (SICCD = 4900 4999, 6000 6999) are excluded. • For the purpose of estimating their betas to obtain systematic risks, firm years in our sample should have at least 60 consecutively previous monthly returns. 45
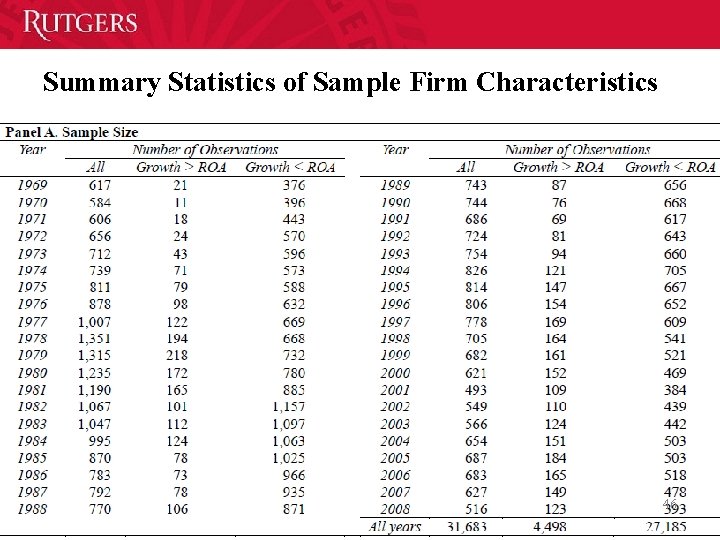
Summary Statistics of Sample Firm Characteristics 46
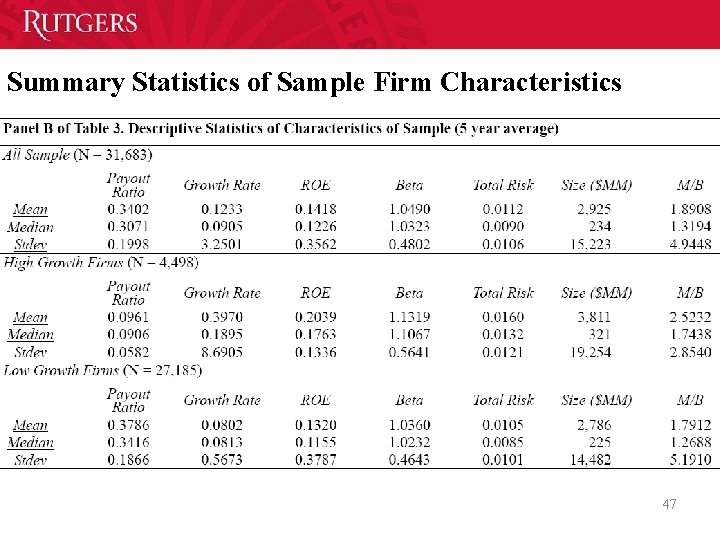
Summary Statistics of Sample Firm Characteristics 47
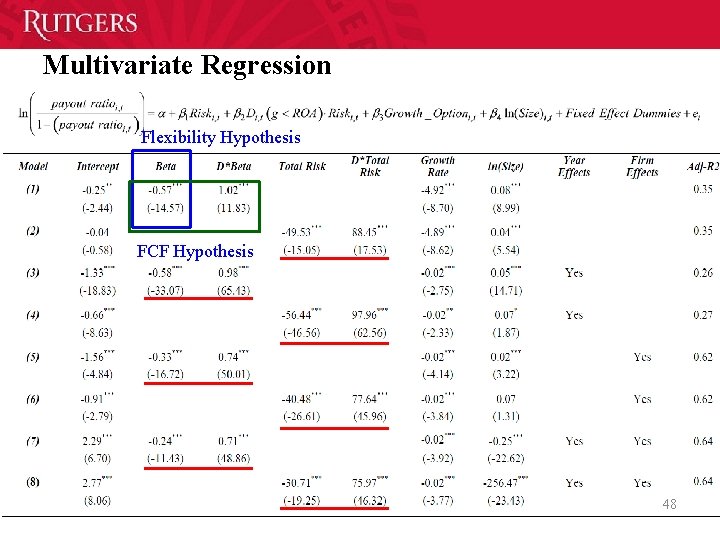
Multivariate Regression Flexibility Hypothesis FCF Hypothesis 48 48
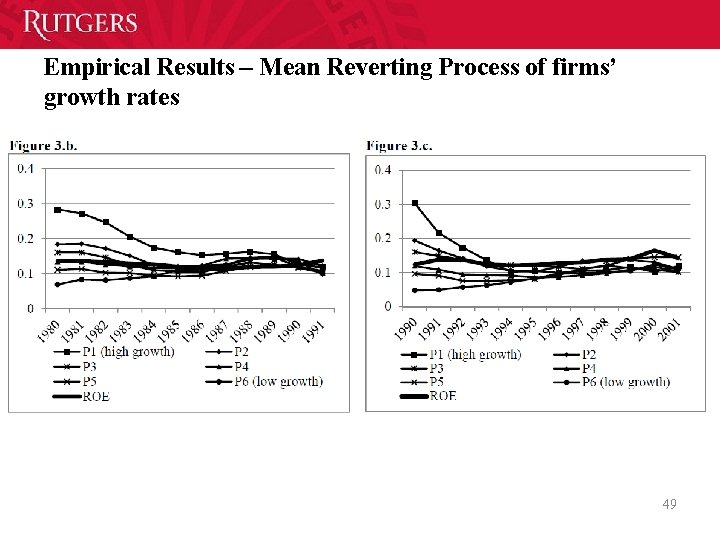
Empirical Results – Mean Reverting Process of firms’ growth rates 49
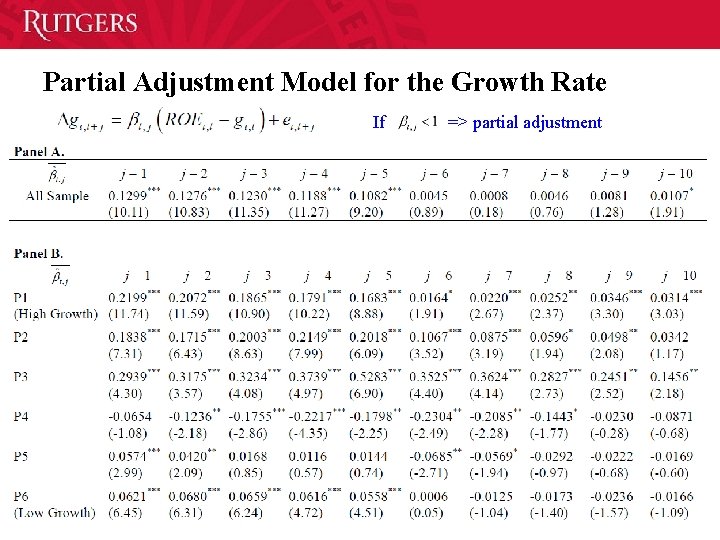
Partial Adjustment Model for the Growth Rate If => partial adjustment 50

Cov. is negatively related to the dividend payouts 51

The higher of the Cov. , the higher possibility to stop the cash dividends. 52

Current vs. Permanent Earnings for Estimating Alternative Dividend Payment Behavioral Model: Theory, Methods and Applications (Lee et al. 2013) The main purposes of this paper are… 1. To theoretically explain why firms generally allocate permanent earnings and transitory earnings between dividends payments and retained earnings 2. To develop alternative methods for decomposing current earnings and dividends into permanent and transitory components 3. To empirically estimate alternative dividend payment behavior models by using two alternative permanent EPS estimates for both individual firms and pooled data 4. To test Lambrecht and Myer’s theoretically results related to alternative dividend payment behavior models. 53

Introduction 1. Earnings of a firm are allocated to retained earnings or dividend payments by a financial decision. 2. The earnings of a firm can be classified into either permanent or transitory components; permanent earning power creates the permanent component, and the transitory component is composed of income of a temporary nature. 3. Forecasts of dividends are important to both security analysts and financial managers, and either conditional or unconditional methods are generally used to forecast dividend payments. 4. Lintner (1956) developed his well known dividend payment behavior model to describe how managers determine their dividend payment. This model has been widely used in finance research (see Marsh and Merton, 1987; Lee and Primeaux, 1991; Garrett and Priestley, 2000; Lambrecht and Myer, 2012). 5. However, using current EPS to estimate Lintner’s dividend behavior model might be also subject to measurement error problem (see Miller and Modigliani, 1966)). 54

Theoretical determination of firm’s permanent and transitory earnings and dividends • The permanent-income hypothesis explains that consumption is not a function of current income but a function of permanent income (Milton Friedman, 1957). Current income is divided into two components: E = EP + ET (1) where E is the current income per share of the firm, EP is the permanent income per share of the firm, and ET is the transitory income per share of the firm. • Dividends can also be divided into two similar components: D = D P + DT (2) where D is the current dividends per share paid by the firm, DP is the permanent dividends per share paid by the firm, and DT is the transitory dividends per share paid by the firm. 55

Theoretical determination of firm’s permanent and transitory earnings and dividends • Permanent dividends are dividends that the business firm systematically pays based on its permanent earnings, dividends paid out of transitory earnings would constitute extra dividends. • All income is either paid out in dividends or retained by the business in the form of retained earnings: E =EP+ ET, E − (DP + DT) − R = 0 (3) where R is the retained earnings per share of the firm, the other terms are as defined in Equations (1) and (2), and ET and DT are ‘‘random” or “chance” variations in income and dividends per share. 56

Theoretical determination of firm’s permanent and transitory earnings and dividends • Different sources of dividend payment (i. e. , permanent or current income) may have different implications in determining a firm’s dividend payment behavior. • This condition provides the motivation for examining both per manent and current earnings per share for describing a firm’s dividend payment behavior in the empirical section of this work. • In the next section, we will discuss alternative methods for decomposing current EPS into permanent and transitory EPS components. 57

Alternative methods for decomposing current EPS into permanent- and transitory-EPS components • Darby’s (1974) method • The relationship between current dividend and permanent earning can be defined as (4) where and are current DPS and permanent EPS for ith firm in period t respectively. • Since permanent earnings are not directly observable, we use Eq. (5) to estimate as: (5) where λi represents the weight used to calculate the permanent earnings per share and C represents the trend rate of EPS growth. • Initial value of permanent EPS EPi, 0 and trend rate C can be derived from Eqs. (6) and (7): Log Ei, t = a 1 + a 2 t + ut (6) (7) 58

Alternative methods for decomposing current EPS into permanent- and transitory-EPS components • Lee and Primeaux’s (1991) method By using the adaptive expectation model, the permanent EPS, EPi, t, can be determined as (9) By Koyck transformation, we can use Eq. (10) to obtain λi for firm i: (10) where • Then, by using estimated λi , current EPS, and initial permanent EPS which was described in Darby’s method, we can estimate permanent EPS in period t. 59

Alternative methods for decomposing current EPS into permanent- and transitory-EPS components • 60

Alternative methods for decomposing current EPS into permanent- and transitory-EPS components • 3. 4 Lambrecht and Myer’s (2012) method • Using the joint determination of manager’s rent and cash dividend payment to equity holders, Lambrecht and Myer (2012) derive a Lintner dividend payment behavior in terms of permanent income as: (14) where and are total dividend payout at time t and t-1 respectively; is the firm’s permanent income at time t. • If the profit margin follows the autoregressive process , then permanent income can be simplified as: (15) where is total operating income without corporate tax for ith firm in period t; is the total debt for ith firm in period t 1; is interest rate; and is the autoregression coefficient for operating income of the firm i. 61

Alternative methods for decomposing current EPS into permanent- and transitory-EPS components • 3. 4 Lambrecht and Myer’s (2012) method • Lambrecht and Myer (2012) claim that Lintner model as traditionally estimated can be defined as: (16) • Their true model is: (17) where ; the current reported earnings is ; and are permanent and transitory components respectively. is the component neither permanent nor transitory component of earnings. SOA is the speed of adjustment; is the constant term of dividend behavior model, it generally used to measure the degree of reluctance to cut dividend, defined as percentage of earnings paid as cash dividend, =1/(1+ ). 62

Alternative methods for decomposing current EPS into permanent- and transitory-EPS components • 3. 4 Lambrecht and Myer’s (2012) method • If does not approach to 1, then equation (17) can be modified as (18) where is the estimated permanent earnings. • Equation (18) is obtained by combining Lambrecht and Myer’s (2012) theory and estimating permanent earnings estimated by either Darby’s or Lee and Primeaux’s method. • This specification takes care both specification errors and the transitory components of earnings. This new specification is most important contribution of this research. 63

Empirical results in estimating three alternative dividend behavior models • Sample • EPS and DPS data of 608 firms from Compustat which has at least 30 years data ended in 2011 to perform the empirical studies (see Appendix C). • The methods used to do the empirical studies include (1) Darby’s method and Lee and Primeaux’s method (2) Lambrecht and Myer’s method (3) combined model as defined in Equation (18) 64

Darby’s and Lee and Primeaux’s methods • We use current and permanent EPS measures to estimate following two alternative dividend payment behavior models as: (19 a) (19 b) (20 a) (20 b) • Following Lee and Chen (2013), we now analyze the biased associated with estimated c 1 and c 2 as follows: Case 1: when (21 a) Case 2: when (21 a) where is the variance of regressing on , and , is the auxiliary regression coefficient of a is the correlation coefficient between and. 65

Darby’s and Lee and Primeaux’s methods • Equations (21 a) and (21 b) imply that the estimated c 1 and c 2 are downward biased. Hence, the estimated intercept as defined in Equation (21 c) is upward biased. (21 c) • Therefore, we need to deal with this kind of errors in variable problem. • First, we use Darby’s and Lee and Primeaux’s methods to estimate permanent EPS. Then we will use DPS and both current EPS and permanent EPS to estimate equations (19 a), (19 b), (20 a), and (20 b) for individual firms and pooled data. 66
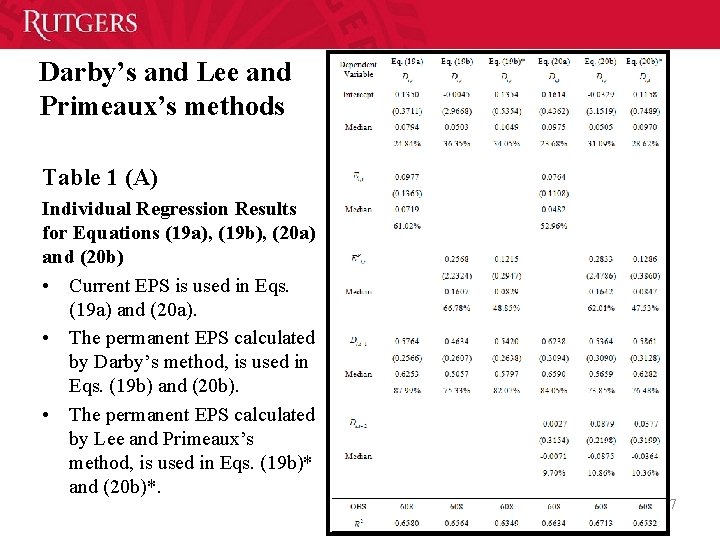
Darby’s and Lee and Primeaux’s methods Table 1 (A) Individual Regression Results for Equations (19 a), (19 b), (20 a) and (20 b) • Current EPS is used in Eqs. (19 a) and (20 a). • The permanent EPS calculated by Darby’s method, is used in Eqs. (19 b) and (20 b). • The permanent EPS calculated by Lee and Primeaux’s method, is used in Eqs. (19 b)* and (20 b)*. 67
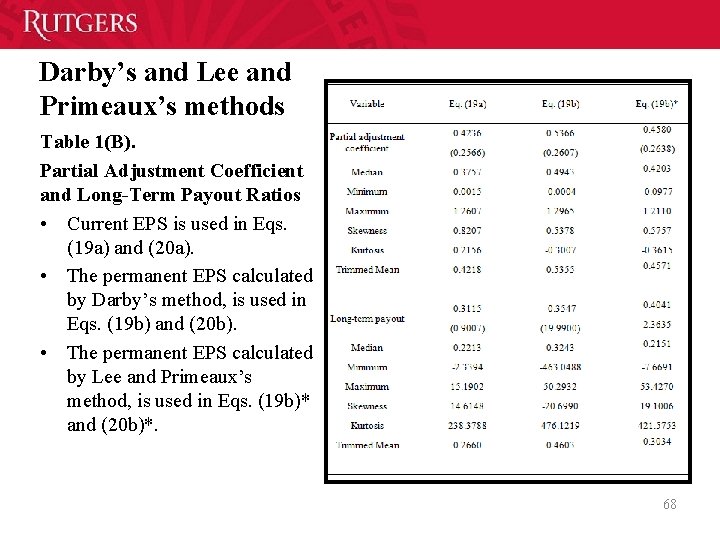
Darby’s and Lee and Primeaux’s methods Table 1(B). Partial Adjustment Coefficient and Long-Term Payout Ratios • Current EPS is used in Eqs. (19 a) and (20 a). • The permanent EPS calculated by Darby’s method, is used in Eqs. (19 b) and (20 b). • The permanent EPS calculated by Lee and Primeaux’s method, is used in Eqs. (19 b)* and (20 b)*. 68
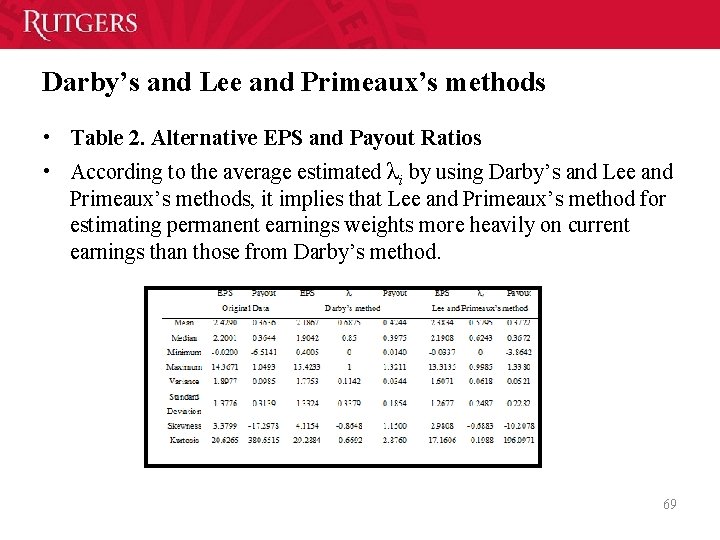
Darby’s and Lee and Primeaux’s methods • Table 2. Alternative EPS and Payout Ratios • According to the average estimated λi by using Darby’s and Lee and Primeaux’s methods, it implies that Lee and Primeaux’s method for estimating permanent earnings weights more heavily on current earnings than those from Darby’s method. 69
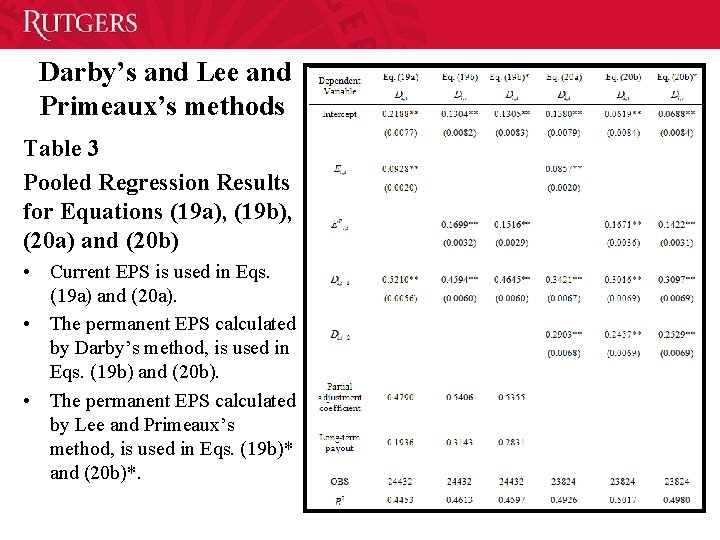
Darby’s and Lee and Primeaux’s methods Table 3 Pooled Regression Results for Equations (19 a), (19 b), (20 a) and (20 b) • Current EPS is used in Eqs. (19 a) and (20 a). • The permanent EPS calculated by Darby’s method, is used in Eqs. (19 b) and (20 b). • The permanent EPS calculated by Lee and Primeaux’s method, is used in Eqs. (19 b)* and (20 b)*. 70

Lambrecht and Myer’s method • Since is not available for individual firm, therefore, we use limiting definition of Lambrecht and Myers’ (2012) method (see equation (15)) to estimate permanent income and apply permanent income to test dividend payment behavior models: (22 a) (22 b) (23 a) (23 b) • In addition, Lambrecht and Myers (2012) show that the Lintner model may be subject to the model misspecification. We therefore test the model misspecification by using Equation (24): (24) 71

Lambrecht and Myer’s method Table 4 Individual Regression Results for Equations (22 a), (22 b), (23 a), (23 b) and (24) • There are 25. 45% of firms whose dividend payouts can be determined by their interest expenses. • It indicates that there exists specification error in Lintner’s model in terms of current earnings. 72

Combined model • We will modify Equation (18) in terms of EPS and DPS as follows: (25 a) (25 b) where Di, t and Di, t-1 are dividend per share for firm i at time t and t-1, respectively; Ei, t and EPi, t are current and permanent EPS for firm i at time t ; Ii, t 1 is the interest expense per share firm i at time t-1. • Eqs. (25 a) and (25 b) can be used to test whether the companies’ annual EPS is following the random walk or not and also to test whether Lambrecht and Myers’s budget constraint in Eq. (26) is held for individual firm or not. (26) where is total dividend payout at time t , and is the total debt in period t and t 1, respectively; is interest rate; is managerial rents at time t; is gross profit at time t. 73
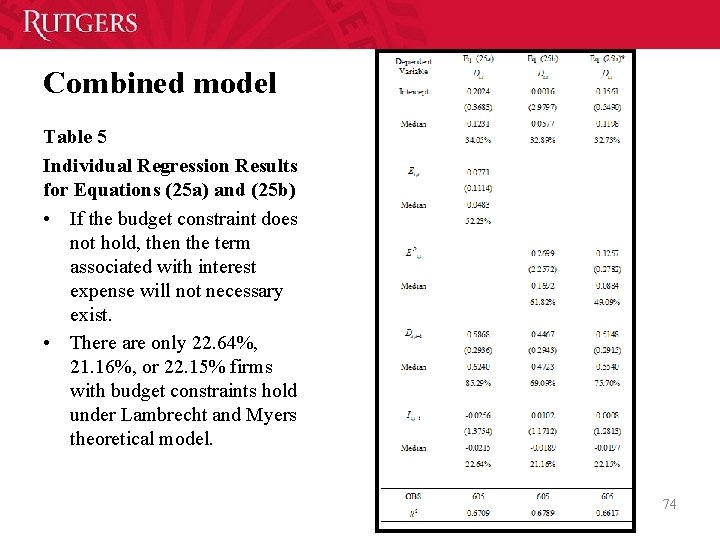
Combined model Table 5 Individual Regression Results for Equations (25 a) and (25 b) • If the budget constraint does not hold, then the term associated with interest expense will not necessary exist. • There are only 22. 64%, 21. 16%, or 22. 15% firms with budget constraints hold under Lambrecht and Myers theoretical model. 74
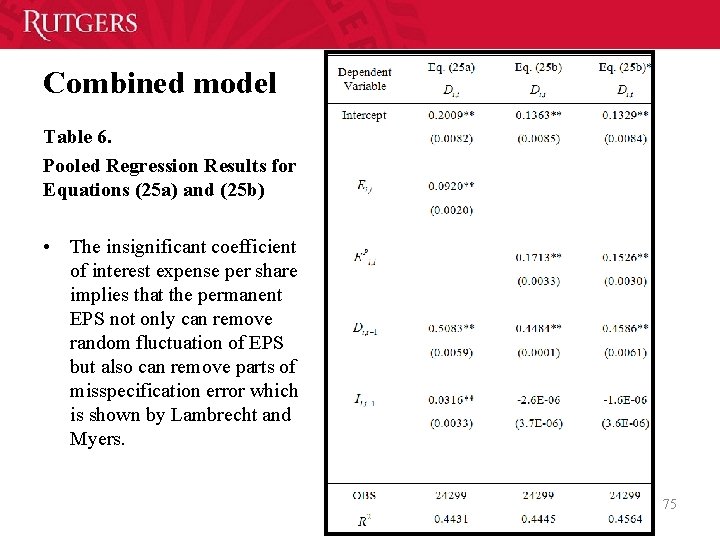
Combined model Table 6. Pooled Regression Results for Equations (25 a) and (25 b) • The insignificant coefficient of interest expense per share implies that the permanent EPS not only can remove random fluctuation of EPS but also can remove parts of misspecification error which is shown by Lambrecht and Myers. 75

Conclusion - 1 • We derive an optimal payout ratio using an exponential utility function to derive the stochastic dynamic dividend policy model. Different from M&M model, our model considers 1) partial payout; 2)uncertainty (risks); 3) stochastic earnings. • A negative relationship between the optimal dividend payout ratio and the growth rate. • The relationship between firm’s optimal payout ratio and its risks depends on its growth rate relative to its ROA. high growth firms pay dividends due to the consideration of flexibility and low growth firms pay dividends due to the 76 consideration of free cash flow problem.

Conclusion - 2 • We derive a dynamic model of optimal growth rate and payout ratio which allows a firm to finance its new assets by retained earnings, new debt, and new equity. • The optimal growth rate follows a convergence processes, and the target rate is firm’s expected ROE. • The firm’s dividend payout is negatively associated with the covariance between the firm’s rate of return on equity and the firm’s growth rate. • The firm tends to pay a dividend if its covariance between the firm’s rate of return on equity and the firm’s growth rate is lower. 77

Potential Future Research 1. Time series v. s. cross sectional research 2. Relationship among discount cash flow, dividend partial adjustment model, and price multiplier model 3. Tax effect on dividend policy in terms of CAPM with dividend Effect 4. Limitations of cross sectional approach to investigate dividend policy 5. We need to use dividend behavior model to supplement cross sectional approach to obtain more meaningful conclusion for decision making. 6. The impacts of Integrated Tax System can be further explored. 78

Conclusion - 3 • Based upon theories and methods developed by Marsh and Merton (1987), Lee and Pri meaux (1991), Garrett and Priestley (2000), and Lambrecht and Myers (2012), we perform both theoretically analyses and empirical studies in this paper. The major findings are: • The average long term payout ratio is downward biased and the average estimated intercept is upward biased when current instead of permanent EPS are used in dividend behavioral model. • We also empirically investigate Lambrecht and Myers’ misspecification issue and find that interest expense per share might be important for estimating dividend behavior model for some firms Future research: • Revise Lambrecht and Myers’ permanent earnings measurement • Extend aggregate dividend behavior model to individual dividend behavior model to test either signaling theory hypothesis or free cash flow 79 hypothesis for individual firms.

Reference • • • • Ang, J. S. (1975). “Dividend Policy: Informational Content or Partial Adjustment? ” Review of Economics and Statistics 57: 65 -70. Ando, A. , and Modigliani. F. (l 963). “The ‘Life Cycle’ Hypothesis of Saving. ” American Economic Review 53: 55 -84. Almeida, H. , M. Campello, and A. F. Galvao Jr. (2010). Measurement errors in investment equations, Review of Financial Studies, 23, 3279 -3328. Bhattacharya, S. , 1979. Imperfect information, dividend policy, and “the bird in the hand” fallacy. Bell J. Econ. 10, 259– 270. Black, F. (1976). “The Dividend Puzzle. ” Journal of Portfolio Management II (Winter): 5 -8. Blau, B. M. , and K. P. Fuller, 2008, Flexibility and dividends, Journal of Corporate Finance 14, 133 -152. Cochran, W. G. (1970). “Some Effects of Errors of Measurement on Multiple Correlation. ” Journal of American Statistical Association 65: 22 -34. Chang H. S. and Lee, c. F. (1977) “Using Pooled Time-Series and Cross Section Data to Test the Firm and Time Effects in Financial Analysis, ” Journal of Financial and Quantitative Analysis Chen, H. Y. , Gupta, M. C. , Lee, A. C. , and Lee, C. F. (2013). “Sustainable Growth Rate, Optimal Growth Rate, and Optimal Payout Ratio: A Joint Optimization Approach. ” Journal of Banking & Finance 37, 1205 -1222. Darby, M. R. (1972). “The Allocation of Transitory Income Among Consumers’ Assets. ” American Economic Review (September): 928 -41. Darby, M. R. (1974), “The Permanent Income Theory of Consumption—A Restatement. ” Quarterly Journal of Economic, (May): 228 -50. De. Angelo, H. , and L. De. Angelo, 2006, The irrelevance of the MM dividend irrelevance theorem, Journal of Financial Economics 79, 293 -315. Dichev, I. D. , and Tang, V. W. (2009) “Earnings volatility and earnings predictability. ” Journal of Accounting and Economics 47, 160– 181. Duesenberry, J. S. (1949). Income, Savings, and the Theory of Consumption Behavior. Cambridge MA: Harvard University Press. Easterbrook, F. H. , 1984. Two agency-cost explanations of dividends. Am. Econ. Rev. 74, 650– 659 80 Eisner, R. (1967). “A Permanent Income Theory of Investment. ” American Economic Review 57: 363 -90. .

Reference • • • • • Eisner, R. (1978). Factors in Business Investment. General Series No. 102. Washington. D. C. : National Bureau of Economic Research Fama, E. F. , and Babiak, H. (1968). “Dividend Policy: An Empirical Analysis. ” Journal of American Statistical Association 63: 1132 -61. Fama, E. F. , and K. R. French, 2001, Disappearing dividends: Changing firm characteristics or lower propensity to pay? Journal of Financial Economics 60, 3 -43. Frankel, R. , and Litov, L. (2009) “Earnings persistence. ” Journal of Accounting and Economics 47, 182– 190. Friedman, M. (1957). A Theory of the Consumption Function. Princeton. NJ: Princeton University Press. Friend, I. and Puckett, M. (1964) “Dividend and Stock Prices” American Economic Review, 54, 656 -682. Garrett, I. and Priestley, R. (2000). “Dividend Behavior and Dividend Signaling. ” The Journal of Financial and Quantitative Analysis (June) 35: 173 -189. Gilmore R. H. and Lee, C. F. (1986) “Empirical Tests of Granger Proposition on Dividend Controversy, ” Review of Economics and Statistics Gordon, M. J. , 1962, The savings investment and valuation of a corporation, Review of Economics and Statistics 44, 37 -51. Granger, C. W. J. (1975) “Some Consequences of The Valuation Model When Expectations Are Taken to Be Optimum Forecasts”. Journal of Finance, 30, 135 -145. Grullon, G. , R. Michaely, and B. Swaminathan, 2002, Are dividend changes a sign of firm maturity? Journal of Business 75, 387 -424. Higgins, R. (1977). “How Much Growth Can a Firm Afford? ” Financial Management 6, 7 -16. Higgins R. C. (1981) “Sustainable growth under Inflation. ” Financial Management 10, 36 -40. Higgins R. C. (2008) Analysis for financial management, 9 th ed. (Mc. Graw-Hill, Inc, New York, NY). Jagannathan, M. , Stephens, C. P. , Weisbach, M. S. , 2000. Financial flexibility and the choice between dividends and stock repurchases. J. Financ. Econ. 57, 355– 384. Jensen, M. C. , 1986. Agency costs of free cash flow, corporate finance, and takeovers. Am. Econ. Rev. 76, 323– 81 329.

Reference • • • • John, K. , Williams, J. , 1985. Dividends, dilution, and taxes: a signaling equilibrium. J. Finance 40, 1053– 1070. Johnston. J. (1972). Econometric Methods, 2 nd ed. New York; Mc. Graw-Hill. Kmenta, J. (1986). Elements of Econometrics, second edition. New York: Macmillan. Lambrecht, B. M. and Myers, S. C. (2012). “A Lintner Model of Payout and Managerial Rents. ” Journal of Finance (October) 67: 1761 -1810 Lang, L. H. P. , Litzenberger, R. H. , 1989. Dividend announcements: cash flow signaling vs. free cash flow hypothesis? J. Financ. Econ. 24, 181– 191 Latane, H. A. , and Jones, C. P. (1979). “Standardized Unexpected Earnings-1971 -77. ” Journal of Finance 34: 71724, Lee, A. C. , J. C. Lee and Lee, C. F. (2009) Financial Analysis, Planning, and Forecasting: Theory and Application, 2 ed. World Scientific Publishing Co. . Lee, C. F. , and Chen, H. Y. (2013). “Alternative Errors-in-Variables Models and Their Applications in Finance Research, ” working paper. Lee, C. F. , M. C. Gupta, H. Y. Chen, and Lee, A. C. (2011) “Optimal payout ratio under uncertainty and the flexibility hypothesis: Theory and empirical evidence. ” Journal of Corporate Finance, 17: 483 -501. Lee, Cheng F. , Shi, J. , 2010. Application of alternative ODE in finance and econometric research. In: Lee, Cheng F. , Lee, Alice C. , John, Lee (Eds. ), Handbook of Quantitative Finance and Risk Management. Springer, pp. 1293– 1300. Lee, C. F. and Han, Dong. (1993). “Dividend Policy under Conditions of Capital Markets and Signaling Equilibrium, ” Review of Quantitative Finance and Accounting. Lee, C. F. , and Primeaux, W. J. (1991). “ Current- Versus Permanent- Dividend Payments Behavioral Model: Methods and Applications, ” Advances in Quantitative Analysis of Finance and Accounting. Vol 1 (Part A) 109 - 130. Lee, C. F. , M. Djarraya, and C. Wu. (1987) “A further empirical investigation of the dividend adjustment process. ” Journal of Econometrics, 267 -285. Lee, C. F. (1976) “Functional Form and the Dividend Effect of the Electric Utility Industry, ” Journal of Finance Leibenstein, H. (1950). “Bandwagon, Snob, and Veblen Effects in the Theory of Consumers’ Demand, ” Quarterly 82 Journal of Economics (May): 183 -207.

• • • • • Lie, E. , 2000. Excess funds and agency problems: an empirical study of incremental cash disbursements. Rev. Financ. Stud. 13, 219– 248. Lintner, J. (1956). “Distribution of Income of Corporations Among Dividends, Retained Earnings, and Taxes. ” American Economic Review (May): 97 -113. Lintner, J. , 1964, Optimal dividends and corporate growth under uncertainty, Quarterly Journal of Economics 78, 49 -95. Litzenberger, R. H, and Ramaswamy, K. , 1982. The Effects of Dividends on Common Stock Prices Tax Effects of Information Effects? J. Finance 37, 429 -443. Marsh, T. A. and Merton, R. C. (1987). “Dividend Behavior for the Aggregate Stock Market. ” The Journal of Business (Jan) 60: 1 -40. Miller, M. H. , and Modigliani, F. (1961). “Dividend Policy, Growth and Valuation of Shares. ” Journal of Business 34 (October): 411 -33. Miller, M. H. , and Modigliani, F. (1966). “Some Estimates of the Coast of Capital to the Electric Utility Industry. ” American Economic Review 56: 334 -91. Miller, M. H. , Rock, K. , 1985. Dividend policy under asymmetric information. J. Finance 40, 1031– 1051. Miller, M. H. , and Scholes, M. S. (1982). “Dividends and Taxes: Some Empirical Evidence. ” Journal of Political Economy. Modigliani, F. , and Miller, M. H. (1958). “The Cost of Capital, Corporation Finance and Theory of Investment. ” American Economic Review 4 B: 261 -97. Modigliani, F. , and Miller, M. H. (1963). “Corporate Income Tax and the Cost of Capital: A Correction. ” American Economic Review 53: 433 -43. Nissim, D. , Ziv, A. , 2001. Dividend changes and future profitability. J. Finance 56, 2111– 2133. Peterson, W. C. (1978). Income. Employment and Growth. 4 th ed. New York: W. W. Norton. Rozeff, M. S. , 1982, Growth, beta and agency costs as determinants of dividend payout ratios, Journal of Financial Research 5, 249 -259. Wallingford, II, B. A. , 1972 a, An inter-temporal approach to the optimization of dividend policy with predetermined investments, Journal of Finance 27, 627 -635. Wang, N. , (2003). “Caballero Meets Bewley: The Permanent-Income Hypothesis in General Equilibrium. ” 83 American Economic Review 93, 927 -936. Weston, F. J. , Brigham, E. , and Besley, S. , (2004) “Essentials of Managerial Finance, ” Cengage South-Western
- Slides: 83