DivideandConquer l Recursive in structure Divide the problem

Divide-and-Conquer l Recursive in structure – Divide the problem into several smaller sub-problems that are similar to the original but smaller in size – Conquer the sub-problems by solving them recursively. If they are small enough, just solve them in a straightforward manner. – Combine the solutions to create a solution to the original problem

An Example: Merge Sort l Divide: Divide the n-element sequence to be sorted into two subsequences of n/2 elements each l Conquer: Sort the two subsequences recursively using merge sort. l Combine: Merge the two sorted subsequences to produce the sorted answer.

Merge-Sort (A, p, r) INPUT: a sequence of n numbers stored in array A OUTPUT: an ordered sequence of n numbers 1. if p < r 2. then q [(p+r)/2] 3. Merge-Sort (A, p, q) 4. Merge-Sort (A, q+1, r) 5. Merge (A, p, q, r)

Analysis of Merge Sort Divide: computing the middle takes (1) l Conquer: solving 2 sub-problem takes 2 T(n/2) l Combine: merging n-element takes (n) l l Total: T(n) = (1) T(n) = 2 T(n/2) + (n) if n = 1 if n > 1 T(n) = (n lg n) (CLRS/Chapter 4)

Recurrence Relations l Recurrences (Chapter 4) – Substitution Method – Iteration Method – Master Method l Arising from Divide and Conquer (e. g. MERGE-SORT) T(n) = (1) T(n) = a T(n/b) + D(n) + C(n) if n c otherwise

Substitution Method l Guessing the form of the solutions, then using mathematical induction to find the constants and show the solution works. l It works well when it is easy to guess. But, there is no general way to guess the correct solution.

An Example l Solve: T(n) = 3 T( n/3 ) + n T(n) 3 c n/3 lg n/3 + n c n lg (n/3) + n = c n lg n - c n lg 3 + n = c n lg n - n (c lg 3 - 1) c n lg n * The last step is true for c 1 / lg 3.

Making a Good Guess l Guessing a similar solution to the one that you have seen before – T(n) = 3 T( n/3 + 5) + n similar to T(n) = 3 T( n/3 ) + n when n is large, the difference between n/3 and (n/3 + 5) is insignificant l Another way is to prove loose upper and lower bounds on recurrence and then reduce the range of uncertainty. – Start with T(n) = (n) & T(n) = O(n 2) T(n) = (n log n)

Subtleties l When the math doesn’t quite work out in the induction, try to adjust your guess with a lower-order term. For example: – We guess T(n) O(n) for T(n) = 3 T( n/3 )+ 4, but we have T(n) 3 c n/3 + 4 = c n + 4 – New guess is T(n) c n - b, where b 0 T(n) 3(c n/3 - b)+4 = c n - 3 b + 4 = c n - b - (2 b-4) Therefore, T(n) c n - b, if 2 b - 4 0 or if b 2

Changing Variables l Use algebraic manipulation to turn an unknown recurrence similar to what you have seen before. – Consider T(n) = 2 T( n 1/2 ) + lg n – Rename m = lg n and we have T(2 m) = 2 T(2 m/2) + m – Set S(m) = T(2 m) and we have S(m) = 2 S(m/2) + m S(m) = O(m lg m) – Changing back from S(m) to T(n), we have T(n) = T(2 m) = S(m) = O(m lg m) = O(lg n lg lg n)

Avoiding Pitfalls l Be careful not to misuse asymptotic notation. For example: – We can falsely prove T(n) = O(n) by guessing T(n) c n for T(n) = 2 T( n/2 ) + n T(n) 2 c n/2 + n cn+n = O(n) Wrong! – The err is that we haven’t proved T(n) c n

Exercises l Solution of T(n) = T( n/2 ) + 1 is O(lg n) l Solution of T(n) = 2 T( n/2 + 17) + n is O(n lg n) l Solve T(n) = 2 T(n 1/2) + 1 by making a change of variables. Don’t worry whether values are integral.

Iteration Method l Expand (iterate) the recurrence and express it as a summation of terms dependent only on n and the initial conditions l The key is to focus on 2 parameters – the number of times the recurrence needs to be iterated to reach the boundary condition – the sum of terms arising from each level of the iteration process l Techniques for evaluating summations can then be used to provide bounds on solution.

An Example l Solve: T(n) = 3 T(n/4) + n T(n) = n + 3 T(n/4) = n + 3[ n/4 + 3 T(n/16) ] = n + 3[n/4] + 9 T(n/16) = n + 3[n/4] + 9 [n/16] + 27 T(n/64) T(n) n + 3 n/4 + 9 n/16 + 27 n/64 + … + 3 log 4 n (1) n (3/4)i + (nlog 43) = 4 n+ o(n) = O(n)

Recursion Trees Keep track of the time spent on the subproblems of a divide and conquer algorithm l A convenient way to visualize what happens when a recursion is iterated l Help organize the algebraic bookkeeping necessary to solve the recurrence l

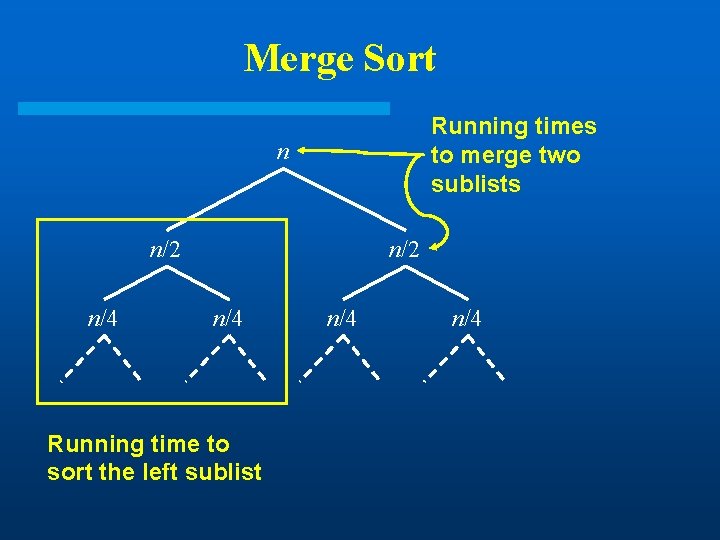
Merge Sort Running times to merge two sublists n n/2 n/4 Running time to sort the left sublist n/4

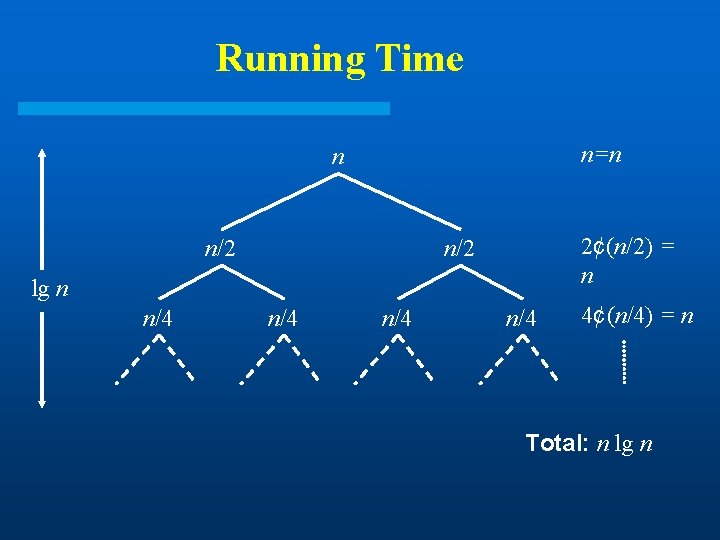
Running Time n=n n n/2 2¢(n/2) = n n/2 lg n n/4 n/4 4¢(n/4) = n Total: n lg n

Recursion Trees and Recurrences l Useful even when a specific algorithm is not specified – For T(n) = 2 T(n/2) + n 2, we have

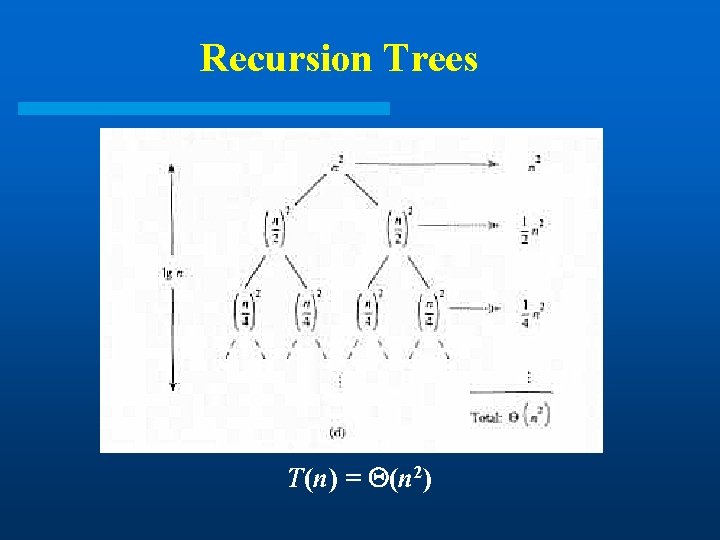
Recursion Trees T(n) = (n 2)

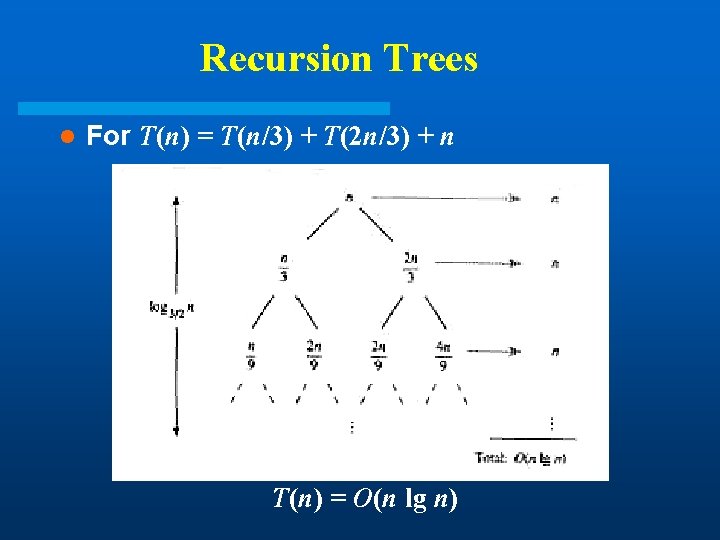
Recursion Trees l For T(n) = T(n/3) + T(2 n/3) + n T(n) = O(n lg n)

Master Method l Provides a “cookbook” method for solving recurrences of the form T(n) = a T(n/b) + f(n) l Assumptions: – a 1 and b 1 are constants – f(n) is an asymptotically positive function – T(n) is defined for nonnegative integers – We interpret n/b to mean either n/b or n/b

The Master Theorem With the recurrence T(n) = a T(n/b) + f(n) as in the previous slide, T(n) can be bounded asymptotically as follows: 1. If f(n)=O(nlogba- ) for some constant > 0, then T(n)= (nlogba). 2. If f(n) = (nlogba), then T(n) = (nlogba lg n). 3. If f(n) = ( nlogba+ ) for some constant > 0, and if a f(n/b) c f(n) for some constant c < 1 and all sufficiently large n, then T(n)= (f(n)).

Simplified Master Theorem Let a 1 and b > 1 be constants and let T(n) be the recurrence T(n) = a T(n/b) + c nk defined for n 0. 1. If a > bk, then T(n) = ( nlogba ). 2. If a = bk, then T(n) = ( nk lg n ). 3. If a < bk, then T(n) = ( nk ).

Examples l T(n) = 16 T(n/4) + n – a = 16, b = 4, thus nlogba = nlog 416 = (n 2) – f(n) = n = O(nlog 416 - ) where = 1 case 1. – Therefore, T(n) = (nlogba ) = (n 2) l T(n) = T(3 n/7) + 1 – a = 1, b=7/3, and nlogba = nlog 7/3 1 = n 0 = 1 – f(n) = 1 = (nlogba) case 2. – Therefore, T(n) = (nlogba lg n) = (lg n)

Examples (Cont. ) l T(n) = 3 T(n/4) + n lg n – a = 3, b=4, thus nlogba = nlog 43 = O(n 0. 793) – f(n) = n lg n = (nlog 43 + ) where 0. 2 case 3. – Therefore, T(n) = (f(n)) = (n lg n) l T(n) = 2 T(n/2) + n lg n – a = 2, b=2, f(n) = n lg n, and nlogba = nlog 22 = n – f(n) is asymptotically larger than nlogba, but not polynomially larger. The ratio lg n is asymptotically less than n for any positive . Thus, the Master Theorem doesn’t apply here.

Exercises l Use the Master Method to solve the following: 1 T(n) = 4 T(n/2) + n 2 3 T(n) = 4 T(n/2) + n 3