Diversification and Portfolio Risk Asset Allocation With Two

Diversification and Portfolio Risk Asset Allocation With Two Risky Assets 6 -1

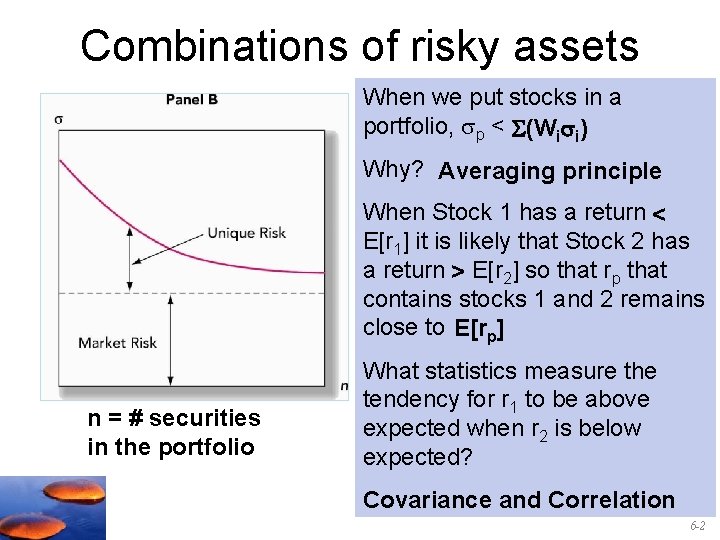
Combinations of risky assets When we put stocks in a portfolio, p < (Wi i) Why? Averaging principle When Stock 1 has a return < E[r 1] it is likely that Stock 2 has a return > E[r 2] so that rp that contains stocks 1 and 2 remains close to E[rp] n = # securities in the portfolio What statistics measure the tendency for r 1 to be above expected when r 2 is below expected? Covariance and Correlation 6 -2

Portfolio Variance and Standard Deviation Variance of a Two Stock Portfolio: 6 -3

Covariance Calculation • Ex ante. Using scenario analysis with probabilities the covariance can be calculated with the following formula: • Ex post. Using a time series of returns, the covariance can be calculated with the following formula: 6 -4

Covariance and correlation • The problem with covariance § § Covariance does not tell us the intensity of the comovement of the stock returns, only the direction. We can standardize the covariance however and calculate the correlation coefficient which will tell us not only the direction but provides a scale to estimate the degree to which the stocks move together. 6 -5

Measuring the correlation coefficient • Standardized covariance is called the correlation coefficient or ___________ For Stock 1 and Stock 2 6 -6

Correlation Coefficients: Possible Values Range of values for correlation coefficients: -1. 0 < < 1. 0 If = 1. 0, the securities would be perfectly positively correlated. If = - 1. 0, the securities would be perfectly negatively correlated. The closer is to -1, the better diversification. 7

and diversification in a 2 stock portfolio zero and less than 1. 0 • Typically is greater than __________ • (1, 2) = (2, 1) and the same is true for the COV • The covariance between any stock such as Stock 1 and itself is simply the variance of Stock 1, • (1, 1) = +1. 0 by definition • We have no measure for how three or more stocks move together. 6 -8

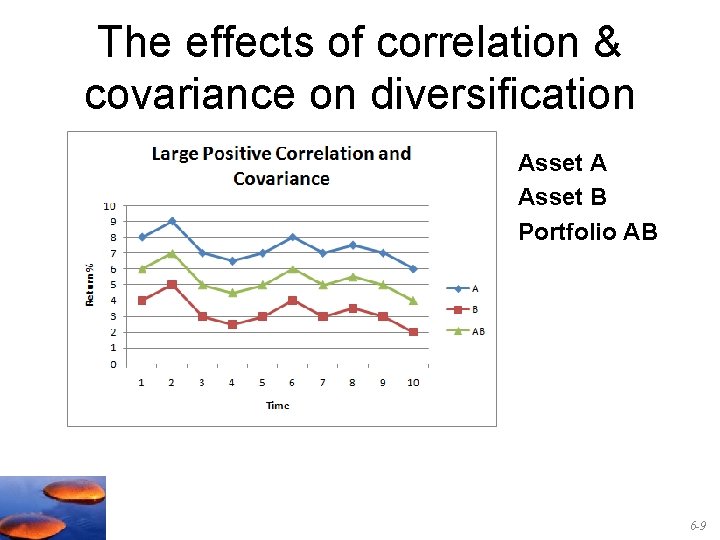
The effects of correlation & covariance on diversification Asset A Asset B Portfolio AB 6 -9

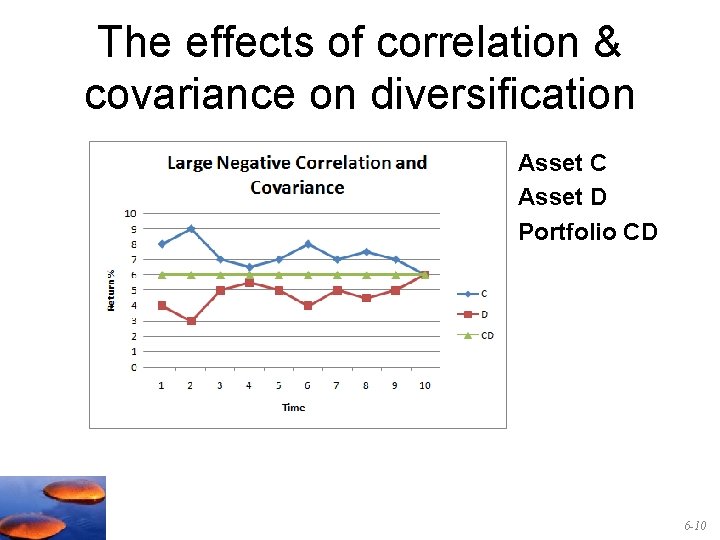
The effects of correlation & covariance on diversification Asset C Asset D Portfolio CD 6 -10

Two-Security Portfolio: Return E(rp )= W 1 r 1 + W 2 r 2 W 1 = Proportion of funds in Security 1 W 2 = Proportion of funds in Security 2 r 1 = Expected return on Security 1 r 2 = Expected return on Security 2 6 -11

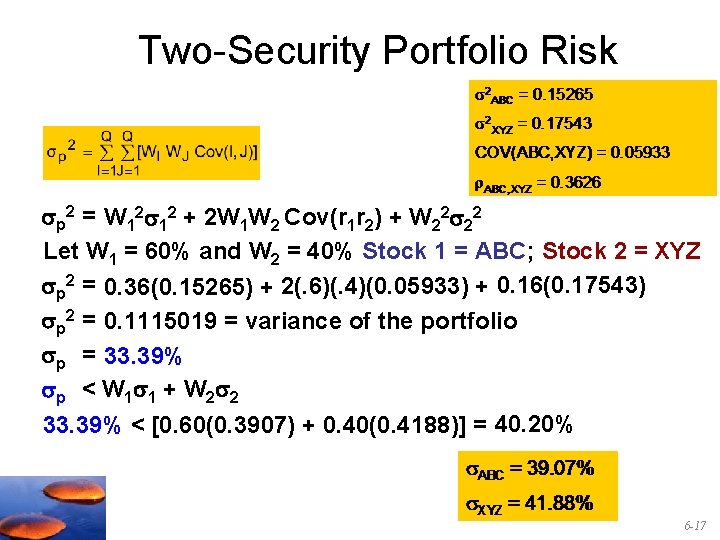
Two-Security Portfolio: Risk p 2 = W 12 12 + W 22 22 + 2 W 1 W 2 Cov(r 1 r 2) 12 = Variance of Security 1 22 = Variance of Security 2 Cov(r 1 r 2) = Covariance of returns for Security 1 and Security 2 6 -12

Example 1: Calculating portfolio risk using a time series of returns – next 4 slides

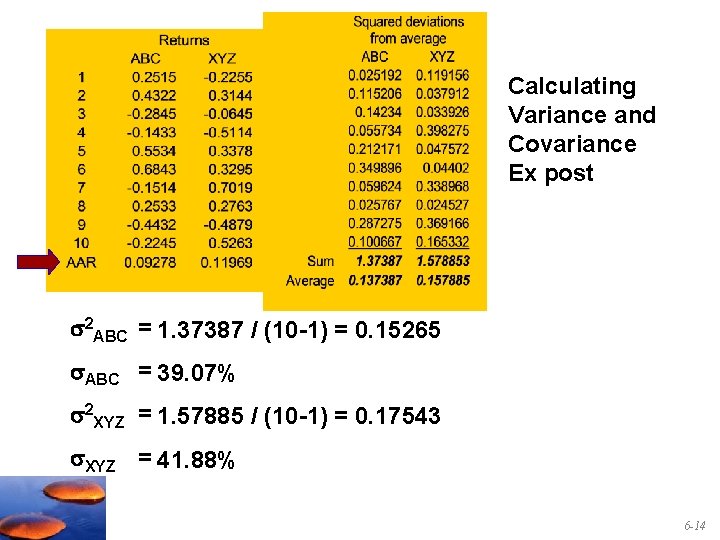
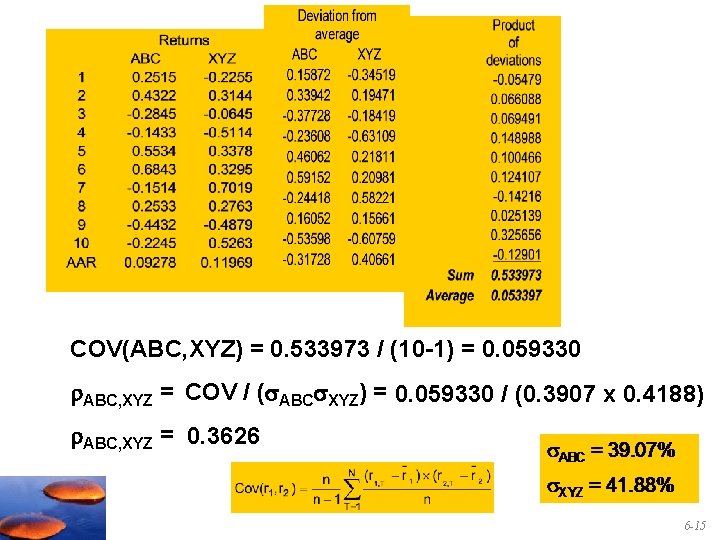
Calculating Variance and Covariance Ex post 2 ABC = 1. 37387 / (10 -1) = 0. 15265 ABC = 39. 07% 2 XYZ = 1. 57885 / (10 -1) = 0. 17543 XYZ = 41. 88% 6 -14

COV(ABC, XYZ) = 0. 533973 / (10 -1) = 0. 059330 ABC, XYZ = COV / ( ABC XYZ) = 0. 059330 / (0. 3907 x 0. 4188) ABC, XYZ = 0. 3626 6 -15

Two-Security Portfolio Return E(rp) = W 1 r 1 + W 2 r 2 W 1 = 0. 6 Wi = % of total money W 2 = 0. 4 invested in security i r 1 = 9. 28% r 2 = 11. 97% E(rp) = 0. 6(9. 28%) + 0. 4(11. 97%) = 10. 36% 6 -16

Two-Security Portfolio Risk p 2 = W 12 12 + 2 W 1 W 2 Cov(r 1 r 2) + W 22 22 Let W 1 = 60% and W 2 = 40% Stock 1 = ABC; Stock 2 = XYZ p 2 = 0. 36(0. 15265) + 2(. 6)(. 4)(0. 05933) + 0. 16(0. 17543) p 2 = 0. 1115019 = variance of the portfolio p = 33. 39% p < W 1 1 + W 2 2 33. 39% < [0. 60(0. 3907) + 0. 40(0. 4188)] = 40. 20% 6 -17

Example 2: Calculating portfolio risk using scenario analysis with probabilities – next 5 slides

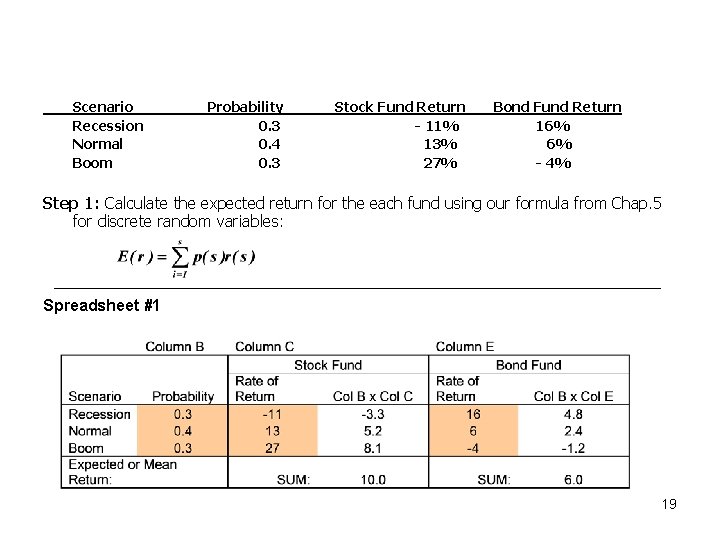
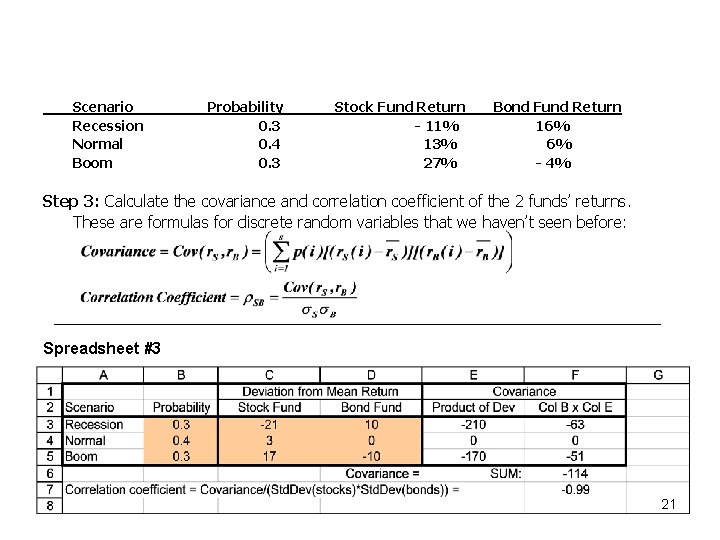
Scenario Recession Normal Boom Probability 0. 3 0. 4 0. 3 Stock Fund Return - 11% 13% 27% Bond Fund Return 16% 6% - 4% Step 1: Calculate the expected return for the each fund using our formula from Chap. 5 for discrete random variables: Spreadsheet #1 19

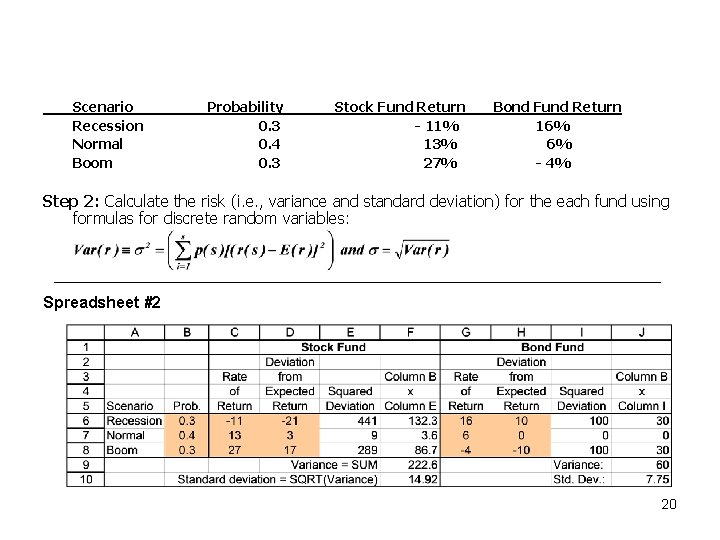
Scenario Recession Normal Boom Probability 0. 3 0. 4 0. 3 Stock Fund Return - 11% 13% 27% Bond Fund Return 16% 6% - 4% Step 2: Calculate the risk (i. e. , variance and standard deviation) for the each fund using formulas for discrete random variables: Spreadsheet #2 20

Scenario Recession Normal Boom Probability 0. 3 0. 4 0. 3 Stock Fund Return - 11% 13% 27% Bond Fund Return 16% 6% - 4% Step 3: Calculate the covariance and correlation coefficient of the 2 funds’ returns. These are formulas for discrete random variables that we haven’t seen before: Spreadsheet #3 21

Step 4: Calculate the expected return of a PORTFOLIO that invests in the stock and bond funds: rp = w B r B + w S r S For example, let’s calculate the return for a portfolio that has 60% of its money invested in the stock fund and 40% of the portfolio invested in the bond fund: rp = w B r B + w S r S = (0. 4)(6. 0%) + (0. 6)(10. 0%) = (2. 4%) = 8. 4% + (6. 0%) 22

Step 5: Calculate the portfolio the risk (i. e. , variance and standard deviation) of a PORTFOLIO that invests in the stock and bond funds: For a portfolio that has 60% of its money invested in the stock fund and 40% of the portfolio invested in the bond fund: s 2 P = (0. 4) 2(0. 0775) 2 + (0. 6) 2(0. 1492) 2 + (2)(0. 4)(0. 6)(0. 0775)(0. 1492) (-0. 99) = 0. 008014 = + 0. 00348, 0. 000961 - 0. 00549 or 0. 348% Standard deviation ( s P ) = √ 0. 00348 = 0. 059, or 5. 9% 23

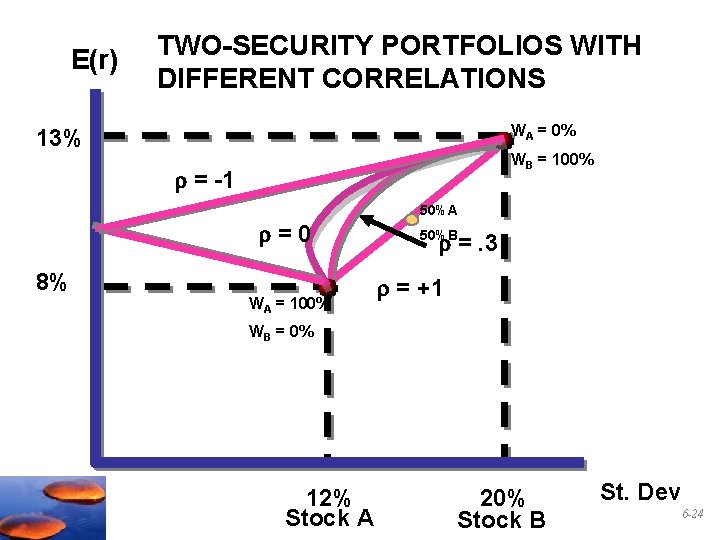
E(r) TWO-SECURITY PORTFOLIOS WITH DIFFERENT CORRELATIONS WA = 0% 13% WB = 100% = -1 =0 8% WA = 100% 50%A =. 3 50%B = +1 WB = 0% 12% Stock A 20% Stock B St. Dev 6 -24

Summary: Portfolio Risk/Return Two Security Portfolio • Amount of risk reduction depends critically or covariances on correlations _____________. <1 • Adding securities with correlations _____ will result in risk reduction. • If risk is reduced by more than expected return, what happens to the return per unit of risk (the Sharpe ratio)? 6 -25

Three-Security Portfolio n or Q = 3 2 p = W 12 12 + W 22 22 + W 32 32 For an n security portfolio there would be _ n variances and n(n-1) covariance terms. _____ The ______ covariances are the dominant effect on 2 p + 2 W 1 W 2 Cov(r 1 r 2) + 2 W 1 W 3 Cov(r 1 r 3) + 2 W 2 W 3 Cov(r 2 r 3) 6 -26

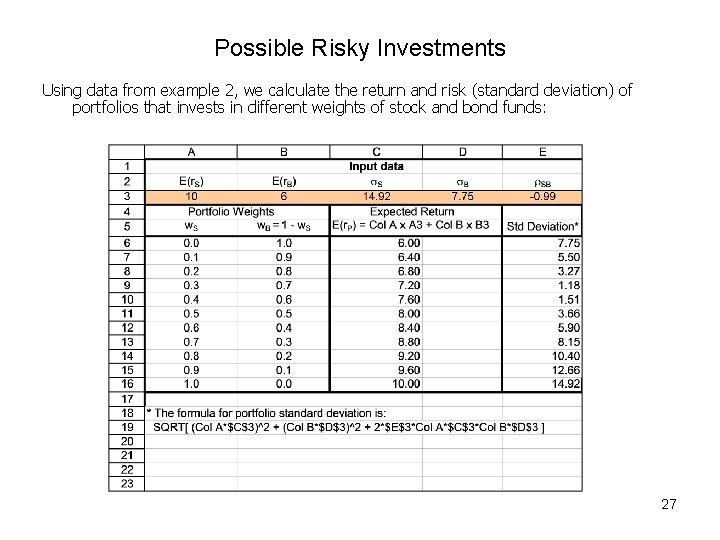
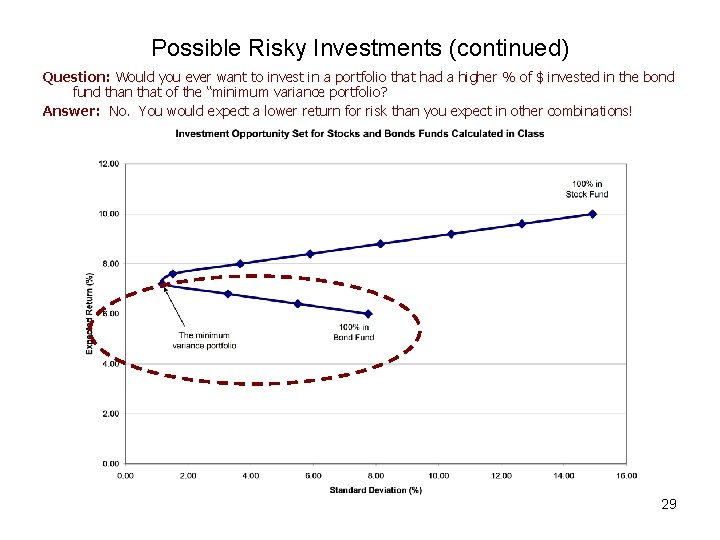
Possible Risky Investments Using data from example 2, we calculate the return and risk (standard deviation) of portfolios that invests in different weights of stock and bond funds: 27

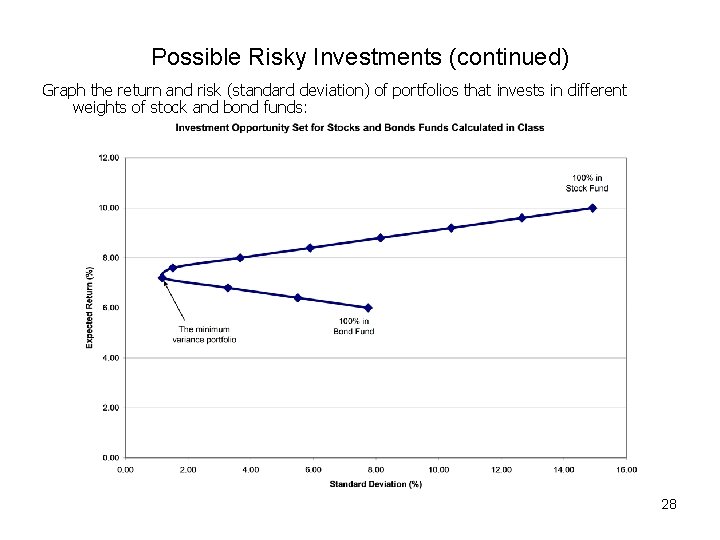
Possible Risky Investments (continued) Graph the return and risk (standard deviation) of portfolios that invests in different weights of stock and bond funds: 28

Possible Risky Investments (continued) Question: Would you ever want to invest in a portfolio that had a higher % of $ invested in the bond fund than that of the “minimum variance portfolio? Answer: No. You would expect a lower return for risk than you expect in other combinations! 29

Minimum Variance Combinations -1< < +1 Choosing weights to minimize the portfolio variance 2 - Cov(r 1 r 2) 2 W 1 = 12 + 22 - 2 Cov(r 1 r 2) W 2 = (1 - W 1) 6 -30

Minimum Variance Combinations -1< < +1 Stk 1 E(r 1) =. 10 Stk 2 E(r 2) =. 14 1 =. 15 12 =. 2 2 =. 20 Cov(r 1 r 2) = 1, 2 1 2 6 -31

Minimum Variance: Return and Risk with r =. 2 1 E[rp] =. 6733(. 10) +. 3267(. 14) =. 1131 or 11. 31% p 2 = W 12 12 + W 22 22 + 2 W 1 W 2 1, 2 1 2 6 -32

Minimum Variance Combination with r = -. 3 1 -. 3 Cov(r 1 r 2) = 1, 2 1 2 6 -33

Minimum Variance Combination with r = -. 3 1 -. 3 E[rp] = 0. 6087(. 10) + 0. 3913(. 14) =. 1157 = 11. 57% p 2 = W 12 12 + W 22 22 + 2 W 1 W 2 1, 2 1 2 Notice lower portfolio standard deviation but higher expected return with smaller 12 =. 2 E(rp) = 11. 31% p = 13. 08% 6 -34

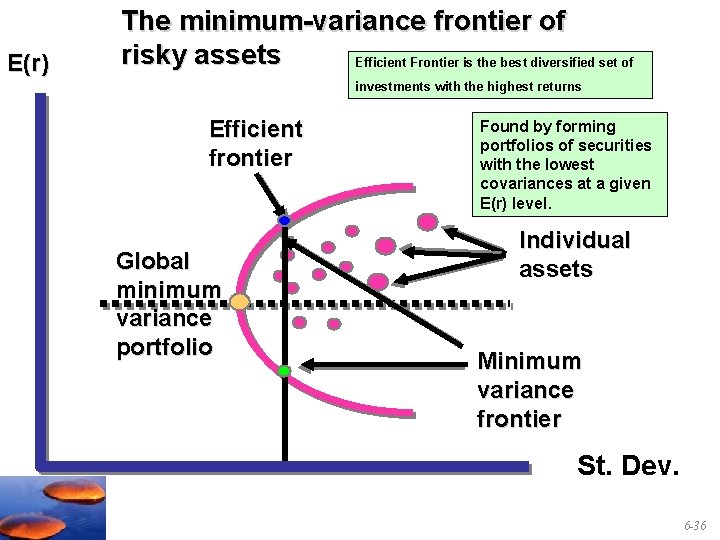
Extending Concepts to All Securities • Consider all possible combinations of securities, with all possible different weightings and keep track of combinations that provide more return for less risk or the least risk for a given level of return and graph the result. • The set of portfolios that provide the optimal trade-offs are described as the efficient frontier. • The efficient frontier portfolios are dominant or the best diversified possible combinations. All investors should want a portfolio on the efficient frontier. … Until we add the riskless asset 6 -35

E(r) The minimum-variance frontier of risky assets Efficient Frontier is the best diversified set of investments with the highest returns Efficient frontier Global minimum variance portfolio Found by forming portfolios of securities with the lowest covariances at a given E(r) level. Individual assets Minimum variance frontier St. Dev. 6 -36

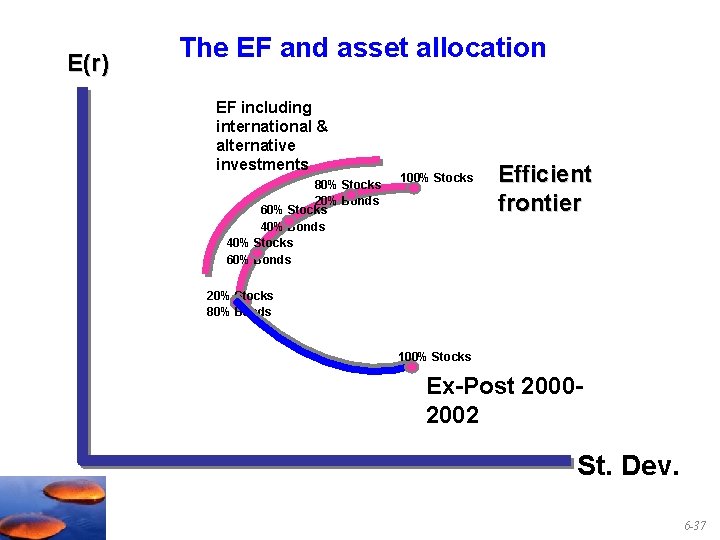
E(r) The EF and asset allocation EF including international & alternative investments 80% Stocks 20% Bonds 60% Stocks 40% Bonds 40% Stocks 60% Bonds 100% Stocks Efficient frontier 20% Stocks 80% Bonds 100% Stocks Ex-Post 20002002 St. Dev. 6 -37