Divergence measures and message passing Tom Minka Microsoft

Divergence measures and message passing Tom Minka Microsoft Research Cambridge, UK with thanks to the Machine Learning and Perception Group 1

Message-Passing Algorithms Mean-field MF [Peterson, Anderson 87] Loopy belief propagation BP [Frey, Mac. Kay 97] Expectation propagation EP [Minka 01] Tree-reweighted message passing TRW [Wainwright, Jaakkola, Willsky 03] Fractional belief propagation FBP [Wiegerinck, Heskes 02] Power EP PEP [Minka 04] 2

Outline • • Example of message passing Interpreting message passing Divergence measures Message passing from a divergence measure • Big picture 3

Outline • • Example of message passing Interpreting message passing Divergence measures Message passing from a divergence measure • Big picture 4

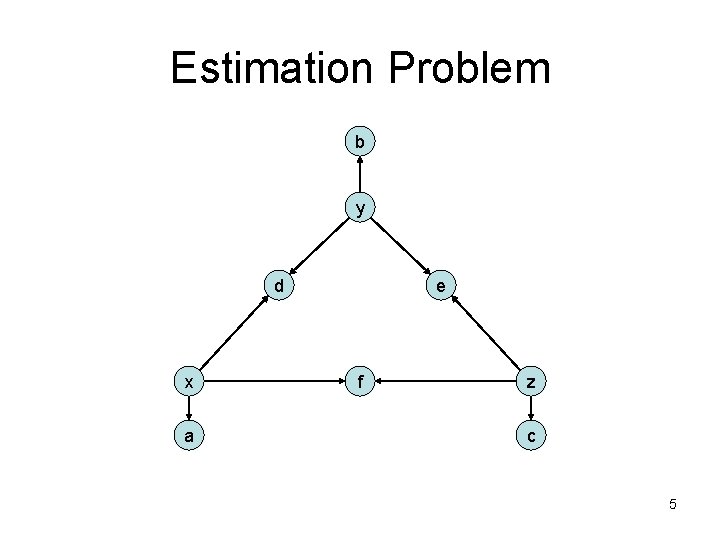
Estimation Problem b y d x a e f z c 5

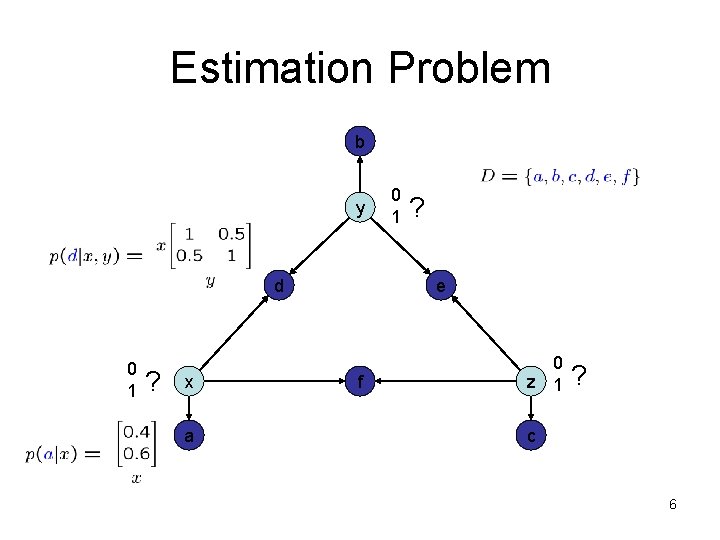
Estimation Problem b y d 0 1 ? x a 0 1 ? e f 0 z 1 ? c 6

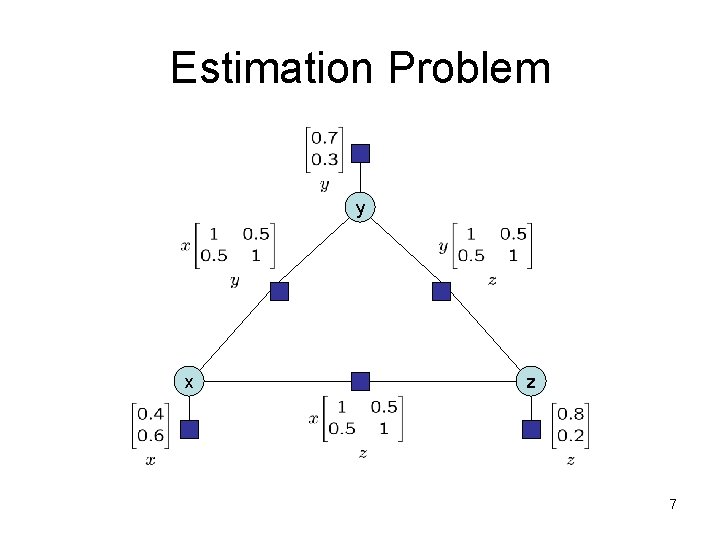
Estimation Problem y x z 7

Estimation Problem Queries: Want to do these quickly 8

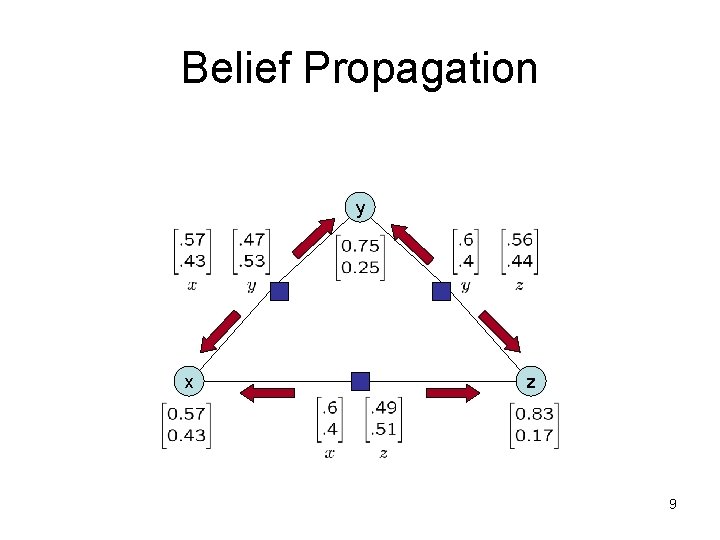
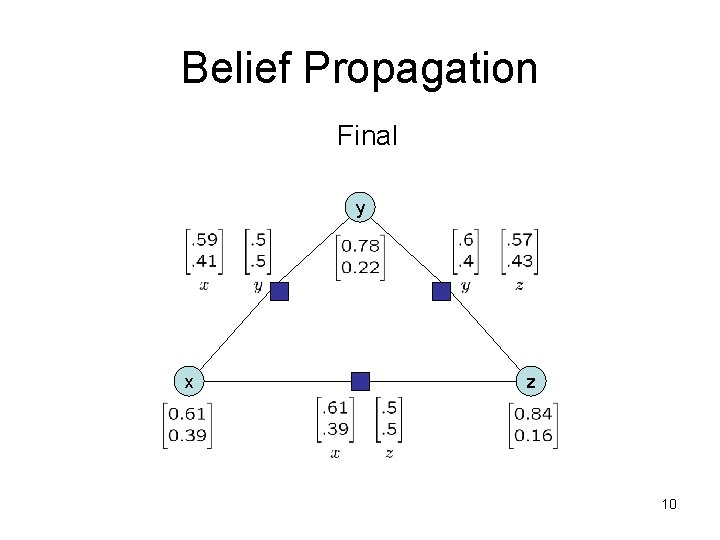
Belief Propagation y x z 9

Belief Propagation Final y x z 10

Belief Propagation Marginals: (Exact) (BP) Normalizing constant: Argmax: 0. 45 (Exact) 0. 44 (BP) (0, 0, 0) (Exact) (0, 0, 0) (BP) 11

Outline • • Example of message passing Interpreting message passing Divergence measures Message passing from a divergence measure • Big picture 12

Message Passing = Distributed Optimization • Messages represent a simpler distribution q(x) that approximates p(x) – A distributed representation • Message passing = optimizing q to fit p – q stands in for p when answering queries • Parameters: – What type of distribution to construct (approximating family) – What cost to minimize (divergence measure) 13

How to make a message-passing algorithm 1. Pick an approximating family • fully-factorized, Gaussian, etc. 2. Pick a divergence measure 3. Construct an optimizer for that measure • usually fixed-point iteration 4. Distribute the optimization across factors 14

Outline • • Example of message passing Interpreting message passing Divergence measures Message passing from a divergence measure • Big picture 15

Let p, q be unnormalized distributions Kullback-Leibler (KL) divergence Alpha-divergence ( is any real number) Asymmetric, convex 16

Examples of alpha-divergence 17

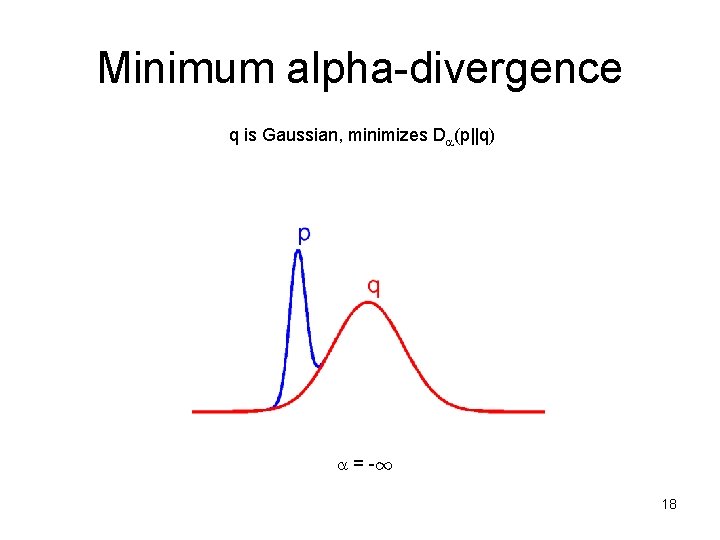
Minimum alpha-divergence q is Gaussian, minimizes D (p||q) = -1 18

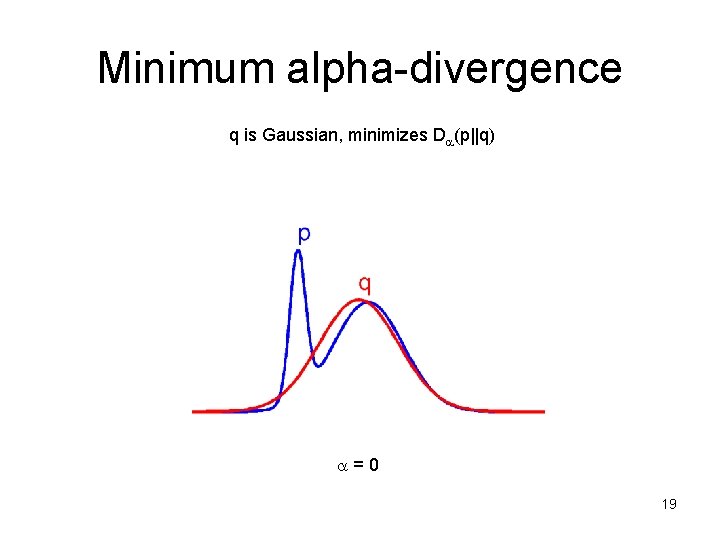
Minimum alpha-divergence q is Gaussian, minimizes D (p||q) =0 19

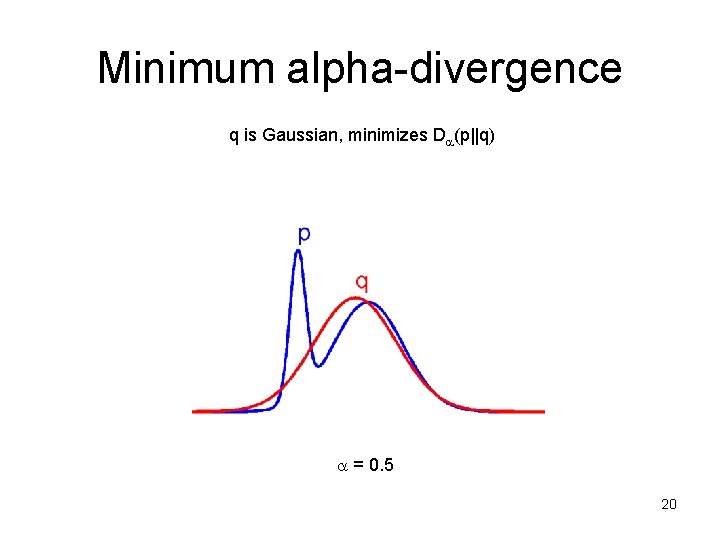
Minimum alpha-divergence q is Gaussian, minimizes D (p||q) = 0. 5 20

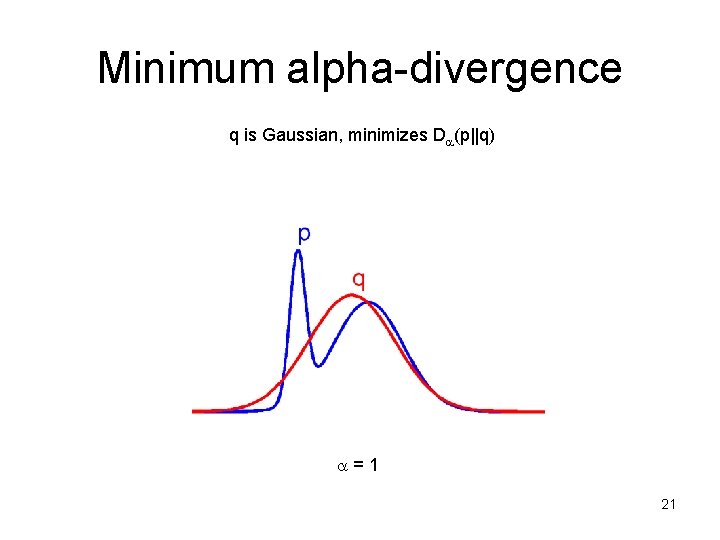
Minimum alpha-divergence q is Gaussian, minimizes D (p||q) =1 21

Minimum alpha-divergence q is Gaussian, minimizes D (p||q) =1 22

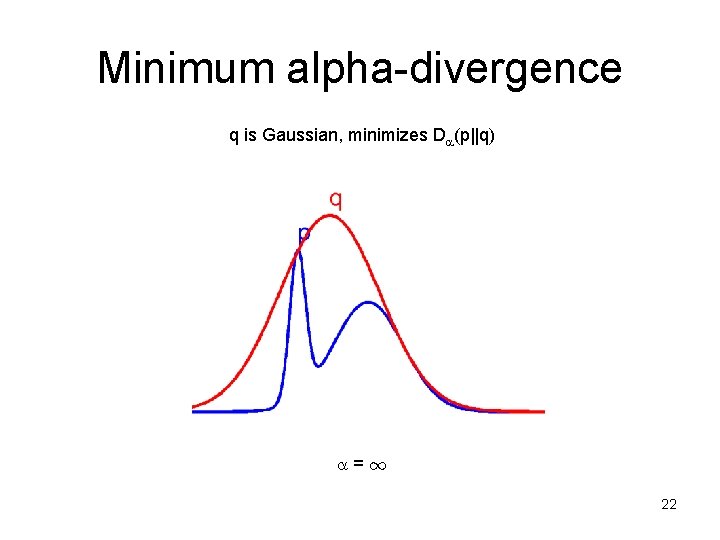
Properties of alpha-divergence • 0 seeks the mode with largest mass (not tallest) – zero-forcing: p(x)=0 forces q(x)=0 – underestimates the support of p • ¸ 1 stretches to cover everything – inclusive: p(x)>0 forces q(x)>0 – overestimates the support of p [Frey, Patrascu, Jaakkola, Moran 00] 23

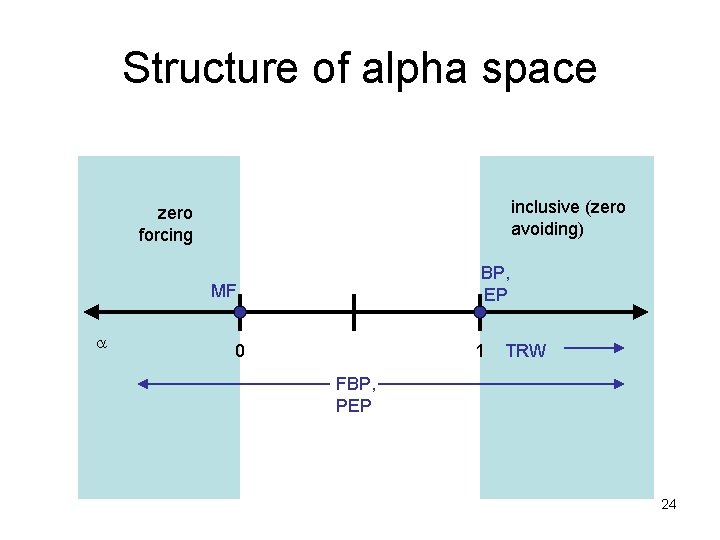
Structure of alpha space inclusive (zero avoiding) zero forcing BP, EP MF 0 1 TRW FBP, PEP 24

Other properties • If q is an exact minimum of alpha-divergence: • Normalizing constant: • If =1: Gaussian q matches mean, variance of p – Fully factorized q matches marginals of p 25

Two-node example x y • q is fully-factorized, minimizes divergence to p • q has correct marginals only for = 1 (BP) 26

Two-node example Bimodal distribution Good Bad • Marginals • Mass • Zeros • Peak heights = 1 (BP) = 0 (MF) 0. 5 • Zeros • Marginals • One peak • Mass 27

Two-node example Bimodal distribution Good Bad • Peak heights • Zeros • Marginals =1 28

Lessons • Neither method is inherently superior – depends on what you care about • A factorized approx does not imply matching marginals (only for =1) • Adding y to the problem can change the estimated marginal for x (though true marginal is unchanged) 29

Outline • • Example of message passing Interpreting message passing Divergence measures Message passing from a divergence measure • Big picture 30

Distributed divergence minimization 31

Distributed divergence minimization • Write p as product of factors: • Approximate factors one by one: • Multiply to get the approximation: 32

Global divergence to local divergence • Global divergence: • Local divergence: 33

Message passing • Messages are passed between factors • Messages are factor approximations: • Factor a receives – Minimize local divergence to get – Send to other factors – Repeat until convergence • Produces all 6 algs 34

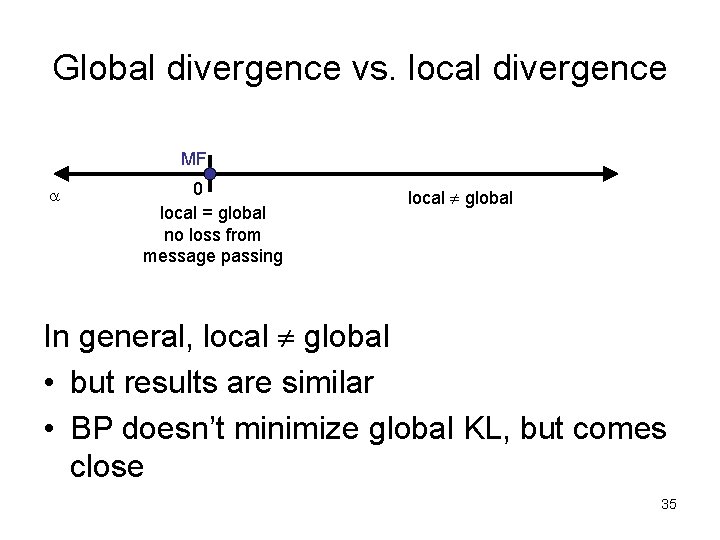
Global divergence vs. local divergence MF 0 local = global no loss from message passing local ¹ global In general, local ¹ global • but results are similar • BP doesn’t minimize global KL, but comes close 35

Experiment • Which message passing algorithm is best at minimizing global D (p||q)? • Procedure: 1. Run FBP with various L 2. Compute global divergence for various G 3. Find best L (best alg) for each G 36

Results • Average over 20 graphs, random singleton and pairwise potentials: exp(wijxixj) • Mixed potentials (w ~ U(-1, 1)): – best L = G (local should match global) – FBP with same is best at minimizing D • BP is best at minimizing KL 37

Outline • • Example of message passing Interpreting message passing Divergence measures Message passing from a divergence measure • Big picture 38

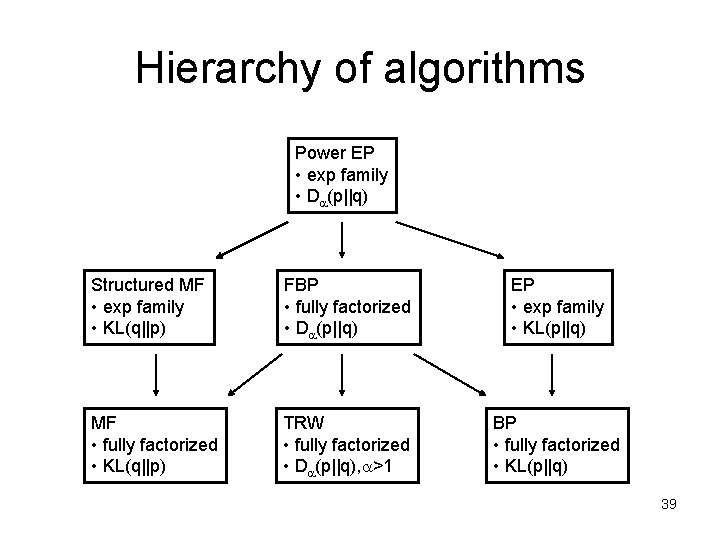
Hierarchy of algorithms Power EP • exp family • D (p||q) Structured MF • exp family • KL(q||p) FBP • fully factorized • D (p||q) EP • exp family • KL(p||q) MF • fully factorized • KL(q||p) TRW • fully factorized • D (p||q), >1 BP • fully factorized • KL(p||q) 39

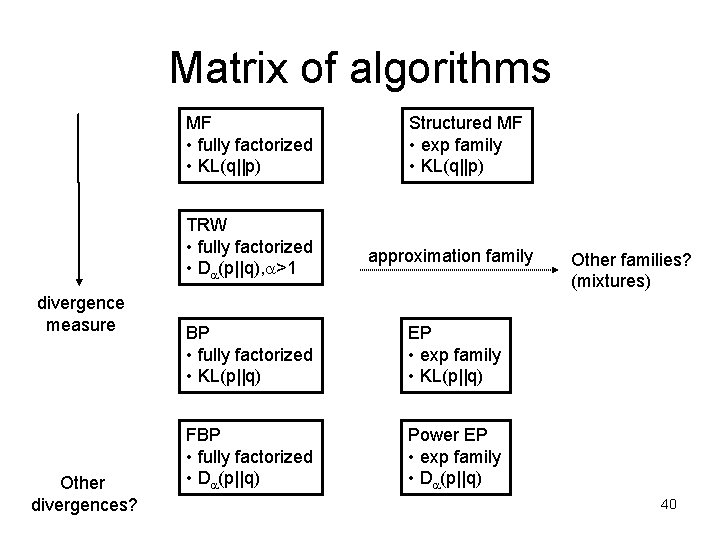
Matrix of algorithms MF • fully factorized • KL(q||p) divergence measure Other divergences? Structured MF • exp family • KL(q||p) TRW • fully factorized • D (p||q), >1 approximation family BP • fully factorized • KL(p||q) EP • exp family • KL(p||q) FBP • fully factorized • D (p||q) Power EP • exp family • D (p||q) Other families? (mixtures) 40

Other Message Passing Algorithms Do they correspond to divergence measures? • Generalized belief propagation [Yedidia, Freeman, Weiss 00] • • • Iterated conditional modes [Besag 86] Max-product belief revision TRW-max-product [Wainwright, Jaakkola, Willsky 02] Laplace propagation [Smola, Vishwanathan, Eskin 03] Penniless propagation [Cano, Moral, Salmerón 00] Bound propagation [Leisink, Kappen 03] 41

Future work • Understand existing message passing algorithms • Understand local vs. global divergence • New message passing algorithms: – Specialized divergence measures – Richer approximating families • Other ways to minimize divergence 42