Divergence Curl Divergence Theorem and Stokes Theorom Divergence

Divergence & Curl Divergence Theorem and Stoke’s Theorom

Divergence (Explanation) �“The divergence of A at a given point P is defined as the outward flux per unit volume as the volume shrinks about P” �It gives the magnitude of a vector field’s source or sink at a particular point.

Divergence ( ) �Flux of vector field A from a closed surface, S: �+ve at source. –ve at sink and 0 where the point is between source and sink

Divergence ( ) �Evaluating divergence of a vector field, A at P(x 0, y 0, z 0) �Step 1: Let the point be enclosed by a differential volume x

Divergence ( ) � �Step 2: Taylor series expansion of A at P gives, �Step 3: Find flux values at front, back etc. Individually and sum them up.

Divergence ( � � )

Divergence ( ) �Add up the individual flux in front and back direction � � Similarly, � �

Divergence ( ) �Summing up everything. = � �Substituting… ( (B) ) � � ( )

Divergence ( � � � )

Divergence ( ) Theorem This is the Divergence Theorem or Gauss. Ostrogradsky Theorem. Things to Remember

Divergence ( ) Theorem Proof: * Subdivide volume, v to large number of small cells * Consider that the outward flux of some cells will be inward flux in some other cells. • So sum of surface integrals over all Sk is same as the surface integral over S • =>

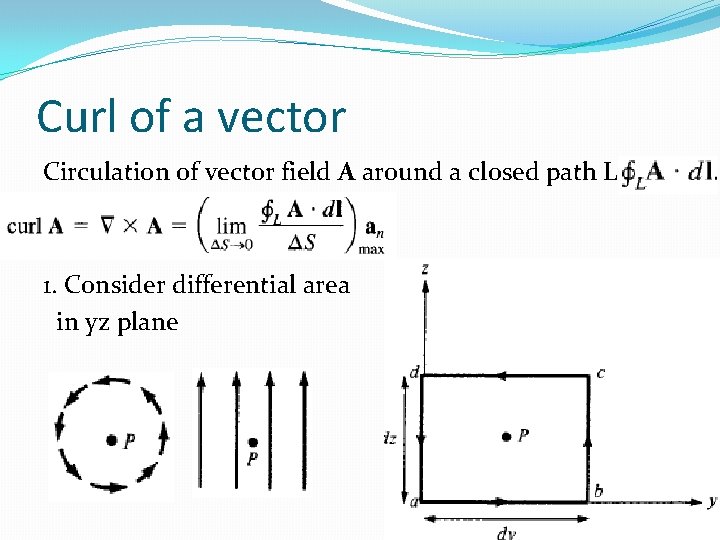
Curl of a vector (Explanation) �“The curl of A is an axial(rotational) vector whose magnitude is the maximum circulation of A per unit area as the area tends to zero and whose direction is the normal direction of the area when the area is oriented to make the circulation maximum. ” �Deals with vector rotations �Direction is found out by Right hand rule. �Magnitude is given by the distance of rotation �If curl is 0, field is static

Curl of a vector Circulation of vector field A around a closed path L 1. Consider differential area in yz plane

Curl of a vector � �Apply taylor series about a center point, P(x 0, y 0, z 0) � � 2. Evaluate components at each sides separately and sum them up. (Length of side and distance to sides)

Curl of a vector �On side ab, �On side bc, �On side cd, �On side da, � � , -

Curl of a vector � � OR

Curl of a vector (Final eqns)

Curl of a vector (Cylindrical)

Curl of a vector (Spherical)

Properties of curl

Stoke’s Theorem � �Stokes's theorem states that the circulation of a vector Field A around a (closed) path L is equal to the surface integral of the curl of A over the open surface S bounded by L provided that A and are continuous on S

Stoke’s Theorem (Proof) �Surface, S is divided into ‘k’ number of sub cells. �If the kth cell has surface area, and is bounded by path Lk

Additional Info �A vector field is said to be solenoidal or divergenceless if �A vector field, A is said to be irrotational or potential if =0