Disusun oleh kelompok 8 Zulkifli Mahardhika adalah metode

adalah metode perhitungan yang didasarkan trapezional rule dan error calcultion sehingga dapat menghasilan nilai

1. Cari nilai A 0, A 2…. . Ak berdasar n dimana n=2^k =

3. Tentukan nilai BK…. . Berdasar nilai Ak…. Dengan Rumus 4. Tentukan nilai CK….

5. Tentukan nilai DK…. . Berdasar nilai Ck…. Dengan Rumus 6. Tentukan nilai EK….

7. Tentukan nilai FK…. . Berdasar nilai Ck…. Dengan Rumus 6. Tentukan nilai GK….

Jika k/pias = 6 maka n = 2^6 =64 64 kali iterasi Rumus untuk

Jika k/pias = 5 maka n = 2^5 =32 32 kali iterasi Rumus untuk

Jika k/pias = 4 maka n = 2^4 =16 16 kali iterasi Rumus untuk

Jika k/pias = 3 maka n = 2^3= 8 8 kali iterasi Rumus untuk

Jika k/pias = 2 maka n = 2^2= 4 4 kali iterasi Rumus untuk

Jika k/pias = 1 maka n = 2^2= 1 2 kali iterasi Rumus untuk

Jika k/pias = 0 maka n = 2^0= 1 1 kali iterasi Rumus untuk

Hitunglah Itegral Dengan Metode Romberg denga 3 pias Dimana diketahui a= 0 b=r Xr

� � a 0=h 0/2[f 0+f 8]=0/2(1+0. 5)=0. 000 a 1=h 1/2[f 0+2 f

Hitunglah Itegral Dengan Metode Romberg denga 4 pias Dimana diketahui a= 0 b=r Xr

a 0= h 0/2[f 0+f 16] = 0/2 *[1+0. 5] =0. 000 a 1=

C 2= B 2+(B 2 -1)/(2^4 -1)= 3. 19121 +(3. 191211. 88889)/15 = 3.

Slides: 23

Download presentation

Disusun oleh kelompok 8 Zulkifli Mahardhika

adalah metode perhitungan yang didasarkan trapezional rule dan error calcultion sehingga dapat menghasilan nilai integral dengan tingkat presisi yang tinggi. Metode integrasi Romberg didasarkan pada perluasan ekstrapolasi Richardson untuk memperoleh nilai integrasi yang semakin baik.

1. Cari nilai A 0, A 2…. . Ak berdasar n dimana n=2^k = jumlah interasi di mana k /pias =(0, 1, 2, 3, 4, 5, 6) 2. Tentukan nilai tabel iterasi diamana r = iterasi ke. Xr = h = ( b-a ) / n fr = Xr yang telah dimasukan ke dalam fungsi/ integral

3. Tentukan nilai BK…. . Berdasar nilai Ak…. Dengan Rumus 4. Tentukan nilai CK…. . Berdasar nilai Bk…. Dengan Rumus

5. Tentukan nilai DK…. . Berdasar nilai Ck…. Dengan Rumus 6. Tentukan nilai EK…. . Berdasar nilai Dk…. Dengan Rumus

7. Tentukan nilai FK…. . Berdasar nilai Ck…. Dengan Rumus 6. Tentukan nilai GK…. . Berdasar nilai DFk…. Dengan Rumus

� Masukan ke dalam tabel Romberg

Jika k/pias = 6 maka n = 2^6 =64 64 kali iterasi Rumus untuk Mencari A dengan 6 pias

Jika k/pias = 5 maka n = 2^5 =32 32 kali iterasi Rumus untuk Mencari A dengan 5 pias Tabel

Jika k/pias = 4 maka n = 2^4 =16 16 kali iterasi Rumus untuk Mencari A dengan 4 pias >>

Jika k/pias = 3 maka n = 2^3= 8 8 kali iterasi Rumus untuk Mencari A dengan 3 pias

Jika k/pias = 2 maka n = 2^2= 4 4 kali iterasi Rumus untuk Mencari A dengan 2 pias

Jika k/pias = 1 maka n = 2^2= 1 2 kali iterasi Rumus untuk Mencari A dengan 1 pias

Jika k/pias = 0 maka n = 2^0= 1 1 kali iterasi Rumus untuk Mencari A dengan 0 pias

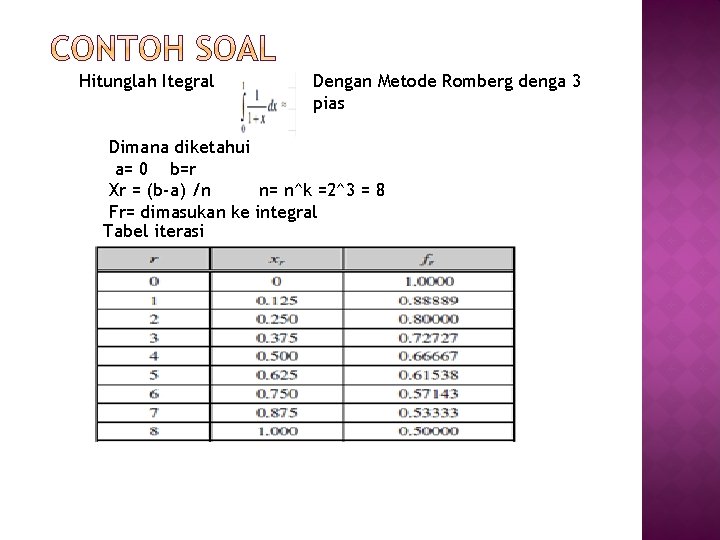
Hitunglah Itegral Dengan Metode Romberg denga 3 pias Dimana diketahui a= 0 b=r Xr = (b-a) /n n= n^k =2^3 = 8 Fr= dimasukan ke integral Tabel iterasi

� � a 0=h 0/2[f 0+f 8]=0/2(1+0. 5)=0. 000 a 1=h 1/2[f 0+2 f 4+f 8]=0. 125/2(1+2(0. 66667)+0. 50000)=0. 17708 a 2=h 2/2[f 0+2 f 2+2 f 4+2 f 6+f 8]=0. 250/2[1+2(0. 80000)+2(0. 66667)+2(0. 5 7143)+0. 50000)=0. 69702 a 3=h 3/2[f 0+2 f 1+2 f 2+2 f 3+2 f 4+2 f 5+2 f 6+f 8]=0. 375/2(1+2*(0. 88889)+2*(0. 80000)+2*(0. 727272)+2*(0. 66667)+2*(0. 61538)+2* � (0. 57143)+2*(0. 53333)+0. 5)=1. 98862 � b 1=a 1+(a 1 -a 0)/(2^2 -1)=0. 17708+(0. 17708 -0. 00)/3=-0. 01389 b 2=a 2+(a 2 -a 1)/(2^2 -1)=0. 69702+(0. 69702 -0. 17708)/3=0. 87033 b 3=a 3+(a 3 -a 2)/(2^2 -1)=1. 98862+(1. 98862 -0. 69702)/3=0. 929278 � � � c 2=b 2+(b 2 -b 1)/(2^4 -1)=0. 87033+(0. 87033 -(-0. 01389))/15=0. 92927 c 3=b 3+(b 3 -b 2)/(2^4 -1)=0. 929278+(0. 929278 -0. 87033)/15=0. 93320 � d 3=c 3+(c 3 -c 2)/(2^6 -1)=0. 93320(0. 93320 -0. 92927)/63=0. 93326 �

Sekian…

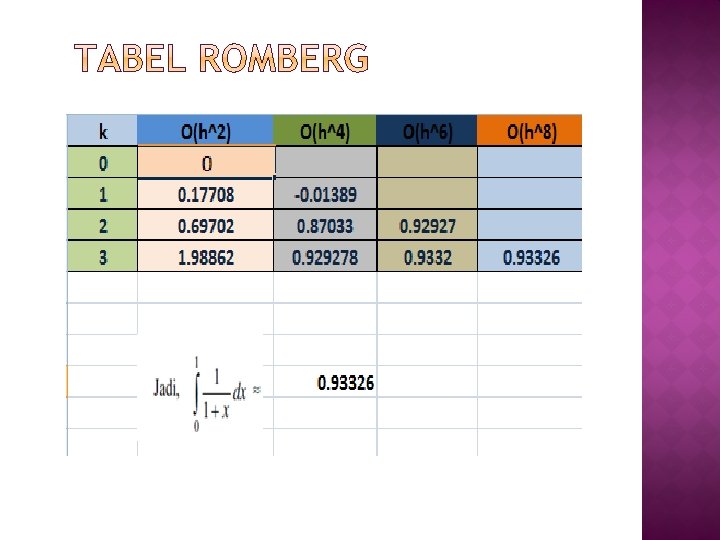
Hitunglah Itegral Dengan Metode Romberg denga 4 pias Dimana diketahui a= 0 b=r Xr = (b-a) /n n= n^k =2^3 = 16 Fr= dimasukan ke integral >>

a 0= h 0/2[f 0+f 16] = 0/2 *[1+0. 5] =0. 000 a 1= h 1/2[f 0+2 f 8+f 16]= 1/2 *(1+2*(0. 66667)+0. 5)= 1. 41667 A 2=h 2/2[f 0+2 f 4+2 f 8+2 f 12+f 16] = 2/2*(1+2*(0. 8)+2*(0. 66667)+*2(0. 57142)+0. 5)= 2. 74758 A 3=h 3/2[f 0+2 f 2+2 f 4+2 f 6+2 f 8. . . . +2 f 14+f 16] = 3/2*[1+2*(0. 8889)+2*(0. 8)+2*(0. 7272)+2*(0. 66667)+2*(0. 61538)+2* (0. 57142)+2* (0. 5333)+0. 5] = 16. 65861 A 4=h 4/2[f 0+2 f 1+2 f 2+2 f 3+2 f 4+2 f 5+2 f 6+2 f 7+2 f 8. . . . +2 f 15+f 16]= 4/2*[1+2*(0. 9411)+2*(0. 8889)+2*(0. 8421)+2*(0. 8)+2*(0. 7619)+2* (0. 7272)+2*(0. 6956)+2*(0. 66667)+2*(0. 64)+2*(0. 61538)+2*(0. 59259)+ 2*(0. 57142)+2*(0. 55172)+2*(0. 5333)+2*(0. 51612)+0. 5] = 44. 376 B 1= B 2= B 3= B 4= a 1+(a 1 -1)/(2^2 -1)= a 2+(a 2 -1)/(2^2 -1)= a 3+(a 3 -1)/(2^2 -1)= a 4+(a 4 -1)/(2^2 -1)= 1. 41667 +(1. 41667 -0. 000)/3 = 1. 88889 2. 74758 +(2. 74758 -1. 41667)/3 = 3. 19121 16. 65861 +(16. 65861 -2. 74758)/3 = 21. 295 44. 376 +(44. 376 -16. 65861)/3 = 53. 61513

C 2= B 2+(B 2 -1)/(2^4 -1)= 3. 19121 +(3. 191211. 88889)/15 = 3. 278031 C 3= B 3+(B 3 -1)/(2^4 -1)= 21. 295 +(21. 2953. 19121)/15 = 22. 50191 C 4= B 3+(B 3 -1)/(2^4 -1)= 53. 61513 +(53. 6151321. 295)/15 = 55. 76980 D 3= C 3+(C 3 -1)/(2^6 -1)= 22. 50191 +(22. 501913. 278031)/63 = 22. 80705 D 4= C 4+(C 4 -1)/(2^6 -1)= 55. 76980 +(55. 7698022. 50191)/63 = 56. 29786 E 4= D 4+(D 4 -1)/(2^8 -1)= 56. 29786 +(56. 2978622. 80705)/255 = 56. 42919

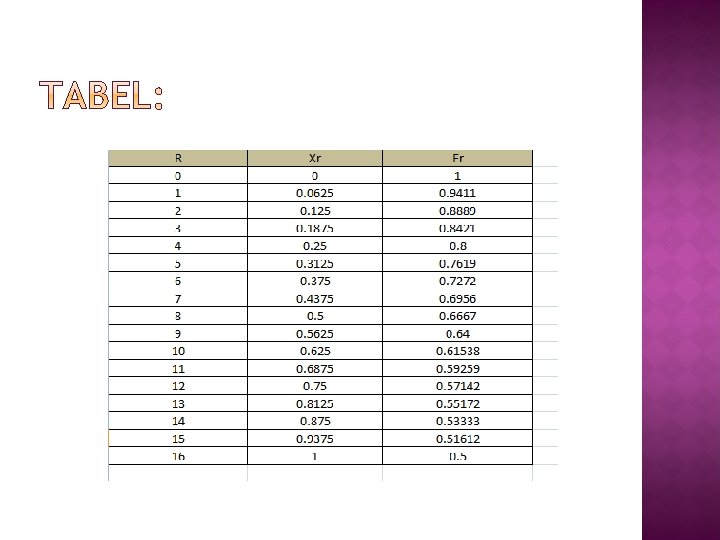
Dengan 4 pias = 56. 42919