Distributive Property 1 Warm Up Objective Students will

Distributive Property 1

Warm Up Objective: Students will be able to apply the distributive property to write equivalent expressions. Language Objective: Students will be able explain how to use the distributive property verbally and in writing. Ronisha and Kalyn are arguing whether the answer to can be found by doing the following work. Do you think this is correct? Explain. 2

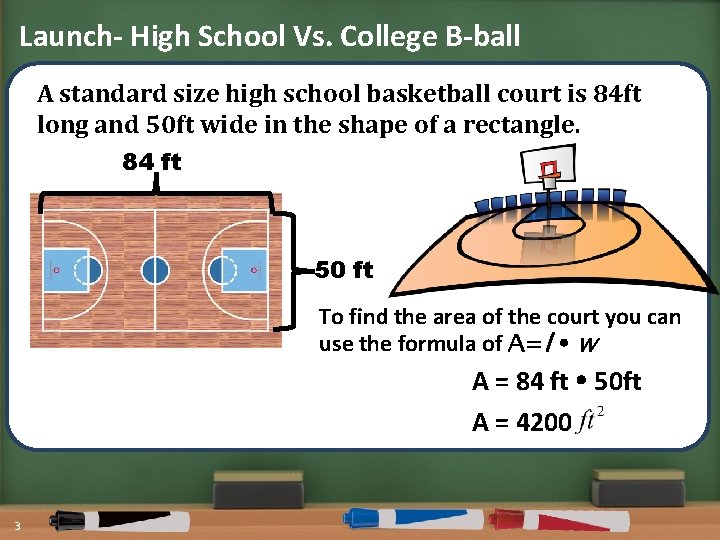
Launch- High School Vs. College B-ball A standard size high school basketball court is 84 ft long and 50 ft wide in the shape of a rectangle. 84 ft 50 ft To find the area of the court you can use the formula of A=l w A = 84 ft 50 ft A = 4200 3

Launch- High School Vs. College B-ball Did you know that a college basketball court is usually 10 ft longer than a high school basketball court? 84 ft 10 ft 50 ft College Basketball Court Can you think of a method to find the area of the college basketball court? 4

Launch- High School Vs. College B-ball 84 ft 10 ft 50 ft Why parenthesis? Method 1 50(84+10) 84+10 94 50 A = 4700 Can you think of a method to find the area of the college basketball court? Method 2 84 50 + 10 50 4200 + 500 A = 4700 What can we say about these two expressions? 55

Explore- Splitting Athletic Fields Ambria lives in a neighborhood with three rectangular fields that all have the same area. The fields are split into different sections for different sports. 20 yds 50 yds 30 yds 120 yds 50 yds 80 yds 6 40 yds

Explore- Splitting Athletic Fields 1. Find the area of this field near Ambria’s house. 50 yds 120 yds 2. This field is divided into two parts. 20 yds 30 yds 120 yds a. Find the area of each part and record your steps as you go. Prove the area is the same as in the first field? 20 120=240 30 120=360 7 +

Explore- Splitting Athletic Fields 20 yds 30 yds 20 120 30 120 yds 20 120=240 30 120=360 b. Write one numerical expression that will calculate the area based on the work you did in part a. c. Find a different way to calculate the area of the entire field and write it as one numerical expression. 20 yds + 30 yds 120 yds 8

Explore- Splitting Athletic Fields 3. The field is divided into two parts. 50 yds 80 yds 40 yds a. Write 2 different numerical expressions that will calculate the area of the entire field. 4. The field below is split into two parts but are missing the dimensions. 50 ______ 100 20 ______ a. Fill in the missing dimensions of the rectangular field whose area can be calculated using the expression. b. Write a different numerical expression to calculate the area of the field. 9

Summary- The Distributive Property 20 yds 50 yds 30 yds 80 yds 40 yds 120 yds Let’s look at the two equivalent ways of finding the area and connect it to an important property in math. The Distributive Property 10

Summary- The Distributive Property 50 yds 80 yds 40 yds 50 600 80 120+ 40 11 50 400 600200 80 40

Summary- The Distributive Property is a property in mathematics which helps to multiply a single term and two or more terms inside parenthesis. Check it out! Lets use the distributive property to write an equal expression. 2 3 + 5 Examples Formal definition 12

Explore- Splitting Athletic Fields 5. An algebraic expression to represent the area of the rectangle below is. 8 x a. Write two different expressions to represent the area of each rectangle below. 5 2 3 x 13 x 4

Explore- Splitting Athletic Fields 6. Use the distributive property to re-write each expression. You may want to draw a rectangle to represent the area. a) 10( a + 7) = ______ b) 7(x + 3)=________ c) x( 3 + 10)= ______ d) a(10 + 9)= ________ e) -2(x + 10)=_______ 14 f) 3 x(x + 10)= _______

Assessment- Exit Slip Who correctly used the distributive property to write an equivalent expression? Provide evidence to support your answer. Riley Michael did because he correctly distributed the 7 to all terms inside the parenthesis. 15