Distributed Systems Part 2 Resource Distributed Computing Principles

Distributed Systems Part 2 • Resource: Distributed Computing, Principles, Algorithms and Systems, Ajay D. Kshemkalyani and Mukesh Singhal, Cambridge University Press, 2008 1

Topology abstraction • Physical topology : The nodes of this topology represent all the network nodes, including switching elements (also called routers), in the WAN and all the end hosts. – In Figure 5. 1(a), the physical topology is not shown explicitly to keep the figure simple. • Logical topology: This is usually defined in the context of a particular application. – The nodes represent all the end hosts where the application executes. – The edges in this topology are logical channels (or logical links) among these nodes. – This view is at a higher level of abstraction that of the physical topology. – Figure 5. 1(b) shows each pair of nodes in the logical topology is connected to give a fully connected network. 2

Terminology and basic algorithms • The topology of a distributed system can be typically viewed as an undirected graph in which the nodes represent the processors and the edges represent the links connecting the processors. – Weights on the edges can represent some cost function we need to model in the application. • There are usually three(not necessarily distinct) levels of topology abstraction that are useful in analyzing the distributed system or a distributed application. These are described using Figure 5. 1. 3

Application Execution and Control Algorithm • The distributed application execution is comprised of the execution of instructions, including the communication instructions, within the distributed application. • A control algorithm also needs to be executed in order to monitor the application execution or to perform various auxiliary functions such as: – creating a spanning tree, creating a connected dominating set, achieving consensus among the nodes, distributed transaction commit, distributed deadlock detection, global predicate detection, termination detection, global state recording, checkpointing, memory consistency enforcement in distributed shared memory systems, etc. • The distributed control algorithm is also termed as a protocol. 4

Spanning Tree • A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. • Hence, a spanning tree does not have cycles and it cannot be disconnected. • By this definition, a conclusion is that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices. • A complete undirected graph can have maximum nn-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 33− 2 = 3 spanning trees are possible (see Figure 5. 2) https: //www. tutorialspoint. com/data_structures_algorithms/spanning_tree. htm 5

Spanning Tree https: //www. tutorialspoint. com/data_structures_algorithms/spanning_tree. htm 6

Centralized and Distributed Algorithms • A centralized algorithm is one in which a predominant amount of work is performed by one control processor, whereas other processors play a relatively smaller role in accomplishing the joint task. – A typical system configuration suited for centralized algorithms is the client–server configuration. • A distributed algorithm is one in which each processor plays an equal role in sharing the message overhead, time overhead, and space overhead. – Difficult to design perfectly distributed algorithms (e. g. , snapshot algorithms, tree-based algorithms) • A snapshot algorithm is used to create a consistent snapshot of the global state of a distributed system 7

Symmetric and Asymmetric Algorithms • A symmetric algorithm (in a distributed environment) is an algorithm in which all the processors execute the same logical functions. • An asymmetric algorithm is an algorithm in which different processors execute logically different (but perhaps partly overlapping) functions. • A centralized algorithm is always asymmetric (depends on the central processor). • An algorithm that is not fully distributed is also asymmetric. • In the client-server configuration, the clients and the server execute asymmetric algorithms. 8

Anonymous Algorithms • In a distributed computation, an anonymous algorithm is an algorithm that neither use process identifiers or processor identifiers to make any execution decision – Anonymous algorithm: process ids or processor ids are not used to make any execution (run-time) decisions • Anonymous algorithms are structurally elegant but hard to design or impossible. 9

Uniform Algorithms • A uniform algorithm (in terms of distributed computation) is an algorithm that does not use n, the number of processes in the system, as a parameter in its code. – A uniform algorithm is desirable because it allows scalability, and processes can join or leave the distributed execution without intruding on the other processes, – except its immediate neighbors that need to be aware of any changes in their immediate topology. 10

Adaptive Algorithms • An adaptive algorithm is an algorithm that changes its behavior at the time it is run based on information available. – Let k (≤ n) be the number of processes participating in the context of a problem X when X is being executed. • Where n is the total number of processes of X. – Computation complexity should be expressible as a function of k, not n (therefore the algorithm is adaptive). • For example, if the complexity of a mutual exclusion algorithm can be expressed in terms of the nodes that are contending for the critical section, then the algorithm would be adaptive. 11

Deterministic vs. Non-deterministic Executions • A deterministic receive primitive specifies the source from which it wants to receive a message – source is explicitly specified. • A non-deterministic receive primitive can receive a message from any source • A distributed program that contains no nondeterministic receives has a deterministic execution; • A distributed program that contains at least one nondeterministic receive primitive, it is said to have a nondeterministic execution. 12

Distributed System Model: Message Ordering • Model the distributed system as a graph. • The following notation is used to refer to messages and events: – When referring to a message mi (without regarding the identity of its sender and receiver processes), its send and receive events are denoted as si and ri, respectively. – send and receive events are denoted simply as s and r. – The transmission of message M causes the following primitives: • send(M), and • receive(M). 13

Distributed System Model: Message Ordering – For any two events a and b (either a send event or a receive event) of a message, the notation a ∼ b denotes that a and b occur at the same process, i. e. , a ∈ Ei and b ∈ Ei for some process i ( where E is the event set). The events a and b are called as corresponding events. – For a given execution E, let the set of all send-receive event pairs (of processes i and j) be denoted as: T = {(s, r) ∈ Ei × Ej |s corresponds to r} • Only send and receive events are considered when dealing with message ordering of a system – because the definition is based on communication events rather than internal events. 14

Message Ordering Paradigms • The order of delivery of messages in a distributed system is an important because it determines the messaging behavior of a distributed program. – Distributed program logic greatly depends on the order of message delivery of the system. • There are four orderings on messages have been defined: – – non-FIFO Causal order Synchronous order 15

Asynchronous Execution • An asynchronous execution (or Aexecution) is an execution for which the causality relation is a partial order: – On any logical link between two nodes in the system, messages delivered in any order, not necessarily FIFO. Such executions are also known as non-FIFO executions. – No causality cycles. – the mode of ordering at the Network Layer in connectionless networks such as IPv 4 is non-FIFO. – Figure 6. 1(a) illustrates an A-execution under non-FIFO ordering. 16

FIFO Execution • A FIFO execution is an A-execution in which, for all (s, r) and (s’, r’) ∈ T, ((s ∼ s’) (r ∼ r’) (s ≺ s’)) ⇒ r ≺ r’. – Messages are delivered in the order in which they are sent (see Figure 6. 1(b)) • Although the logical link is inherently non-FIFO, most network protocols provide a connection-oriented service at the transport layer. – To implement a FIFO logical channel over a non-FIFO channel the following parameters are important: • Source processes, messages sending order, message buffering at receiver, destination processes, message receiving order, channel delay information, etc. 17

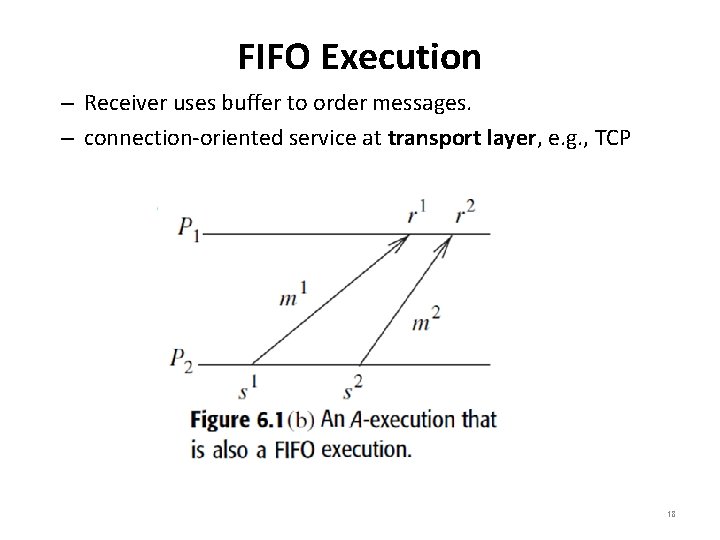
FIFO Execution – Receiver uses buffer to order messages. – connection-oriented service at transport layer, e. g. , TCP 18

Causally Ordered (CO) Executions • A CO execution is an A-execution in which, for all (s, r) and (s’, r’) ∈ T, ((r ∼ r’) (s ≺ s’)) ⇒ (r ≺ r’) • If two send events s and s’ are related by causality ordering, then a causally ordered execution requires that their corresponding receive events r and r’ occur in the same order at destinations. – Figure 6. 2(a) shows an execution that violates CO because s 1 ≺ s 3 and at the common destination P 1, we have r 3 ≺ r 1 (m 1 overtaken by chain <m 2, m 3>). – Figure 6. 2(b) shows an execution that violates CO because s 3 ≺ s 2 at common destination P 2, we have r 2 ≺ r 3 – Figure 6. 2(c) shows an execution that satisfies CO. No send events are related by causality. – Figure 6. 2(d) shows an execution that satisfies CO. s 2 and s 1 are related by causality but the destinations of the corresponding messages are different. Similarly for s 2 and s 3. 19

Causally ordered (CO) executions 20

Causally ordered (CO) executions • CO is useful for applications requiring updates to shared data, implementing distributed shared memory, and fair resource allocation such as granting of requests for distributed mutual exclusion: – Need to distinguish between the arrival of a message and its delivery to implement CO. A message m that arrives in the local OS buffer at Pi may have to be delayed until the messages that were sent to Pi causally before m was sent. The delayed message m is then given to the application for processing. – The event of an application processing an arrived message is referred to as a delivery event. – Figure 6. 2(a) shows an execution that violates CO. To enforce CO, message m 3 should be kept pending in the local buffer after it arrives at P 1, until m 1 arrives and m 1 is delivered. 21

Causally ordered (CO) executions • Definition of causal order (CO): If {send(m 1) ≺ send(m 2)} then for each common destination d of messages m 1 m 2, {deliverd (m 1) ≺ deliverd (m 2)} must be satisfied. • In a FIFO execution, no message can be overtaken by another message between the same (sender, receiver) pair of processes. • The FIFO property which applies on a per-logical channel basis can be extended globally to give the CO property. • Figure 6. 2(a) shows an execution that violates CO. Message m 1 is overtaken by the messages in the chain < m 2, m 3>. 22

Causally ordered (CO) executions • The message m’ sent causally later than m is not received causally earlier at the common destination. This ordering is known as message ordering (MO). • Definition of Message order (MO): A MO execution is an Aexecution in which, for all (s, r) (s’, r’) ∈ T, (s ≺ s’) ⇒ (r’ ≺ r). • Consider any message pair, say m 1 and m 3 in Figure 6. 2(a). s 1 ≺ s 3 but ￢(r 3 ≺ r 1) is false. Hence, the execution does not satisfy MO. • Another characterization of a CO execution in terms of the partial order is known as the empty-interval (EI) property: – Consider the message m 2 in Figure 6. 2(b). There does not exist any event x such that s 2 ≺ x ≺ r 2. This holds for all messages in the execution. Hence, the execution is EI. 23

Synchronous Executions • If we require that the past of both the s and r events are identical we get a subclass of CO executions, called synchronous executions (see Figure 6. 3(b)) • When all the communication between pairs of processes uses synchronous send and receive primitives, the resulting order is the synchronous order. • As each synchronous communication involves a handshake between the receiver and the sender, – the corresponding send and receive events can be viewed as occurring instantaneously and atomically. 24

Synchronous Executions • Figure 6. 3(a) shows a synchronous execution on an asynchronous system. • The “instantaneous communication” property of synchronous executions requires a modified definition of the causality relation because for each (s, r) ∈ T, the send event is not causally ordered before the receive event. – The two events are viewed as being atomic and simultaneous, and neither event precedes the other. 25

Synchronous Executions 26

Synchronous Executions 27

Synchronous Executions 28

Asynchronous Execution with Synchronous Communication • When all the communication between pairs of processes is by using synchronous send and receive primitives, the resulting order is synchronous order. • The send and receive events of a message appear instantaneous, see the example in Figure 6. 3. • If a program is written for an asynchronous system, will it still execute correctly if the communication is done by synchronous primitives instead? – There is a possibility that the program may deadlock, as shown by the code in Figure 6. 4. Because the messages send by two processes each other never occurs at the same time! 29

Asynchronous Execution with Synchronous Communication • Charron-Bost et al. [7] observed that a distributed algorithm designed to run correctly on asynchronous systems (called Aexecutions) may not run correctly on synchronous systems. • An algorithm that runs on an asynchronous system may deadlock on a synchronous system. 30

Asynchronous Execution with Synchronous Communication • The asynchronous execution of Figure 6. 4, illustrated in Figure 6. 5(a) using a timing diagram, will deadlock if run with synchronous primitives. The executions in Figure 6. 5(b)–(c) will also deadlock when run on a synchronous system. 31

Executions Realizable with Synchronous Communication (RSC) • An execution can be modeled (using the interleaving model) as a feasible schedule of the events to give a total order that extends the partial order (E≺). • In an A-execution, the messages can be made to appear instantaneous if there exists a linear extension of the execution, such that each send event is immediately followed by its corresponding receive event in this linear extension. • Such an A-execution can be realized under synchronous communication and is called a realizable with synchronous communication (RSC) execution. 32

Executions realizable with synchronous communication (RSC) 33

Executions realizable with synchronous communication (RSC) 34

Executions realizable with synchronous communication (RSC) 35

Executions realizable with synchronous communication (RSC) 36

Distributed MUTEX Algorithm • Mutual exclusion (Mutex) is a fundamental problem in distributed computing systems. • Mutex ensures that concurrent access of processes to a shared resource or data is serialized, that is, executed in a mutually exclusive manner. • Mutex in a distributed system states that only one process is allowed to execute the critical section (CS) at any given time. • In a distributed system, message passing is the sole means for implementing distributed mutex. – The decision to which process is allowed access to the CS next is based on the state of all processes involved in the computation and it should deliver in some consistent way. 37

Distributed MUTEX Algorithm • The design of distributed mutual exclusion algorithms is complex due to unpredictable message delays and incomplete knowledge of the system state. • There are three basic approaches for implementing distributed mutex: 1. Token-based approach. 2. Non-token-based approach. 3. Quorum-based approach. 38

Approaches for Distributed Mutex • Token-based approach: – A unique token (a privilege message) is shared among the sites. – A site is allowed to enter its CS if it possesses the token. – Mutex is ensured because the token is unique. • Non-token based approach: – Two or more successive rounds of messages are exchanged among the sites to determine which site will enter the CS next. • A site enters its CS when an assertion, defined on its local variables becomes true. • Quorum based approach: – Each site requests permission to execute the CS from a subset of sites (called a quorum). Any two quorums contain a common site. • This common site is responsible to make sure that only one request executes the CS at any time. 39

System Model • The system consists of N sites, S 1, S 2, . . . , SN. • Assume that a single process is running on each site. The process at site Si is denoted by pi. – All these processes communicate asynchronously over an underlying communication network. • A site can be in one of the following three states: – requesting the CS, executing the CS, or neither requesting nor executing the CS (idle). • In the requesting the CS state, the site is blocked and can not make further requests for the CS. In the idle state, the site is executing outside the CS. • In token-based algorithms, a site can also be in a state where a site holding the token is executing outside the CS (called the idle token state). • At any instant, a site may have several pending requests for CS. A site queues up these requests and serves them one at a time. 40

System Model - Assumptions • At this moment, there are no assumptions regarding communication channels such as: – If they are FIFO or not. – This is algorithm specific. – We assume that channels reliably deliver all messages, sites do not crash, and the network does not get partitioned. • Many algorithms use Lamport style logical clocks to assign a timestamp to CS requests. • Timestamps are used to decide the priority of requests in case of a conflict. – The general rule followed is that the smaller the timestamp of a request, the higher its priority to execute the CS. 41

Requirements of Mutex Algorithms • Safety Property: – At any instant, only one process can execute the CS. • Liveness Property: – This property states the absence of deadlock and starvation. • Two or more sites should not endlessly wait for messages that will never arrive. • A site must not wait indefinitely to execute the CS while other sites are repeatedly executing the CS. • Every requesting site should get an opportunity to execute the CS in finite time. • Fairness: – Each waiting process gets a fair chance to execute its CS. • The CS execution requests are executed in the order of their arrival (time is determined by a logical clock) in the system. 42

Performance Matrix 43

Performance Matrix 44

Performance Matrix • Low and High Load Performance: – The performance of mutex algorithms under two special loading conditions, viz. , low load and high load. – The load is determined by the arrival rate of CS execution requests. – Under low load conditions, there is seldom more than one request for the CS present in the system simultaneously. – Under heavy load conditions, there is always a pending request for CS at a site. 45

Lamport’s Mutex Algorithm • Lamport developed a distributed mutual exclusion algorithm as an illustration of his clock synchronization scheme. • A request for CS are executed in the order of their timestamps and is determined by logical clocks. • When a site processes a request for the CS, it updates its local clock and assigns the request a timestamp. • The algorithm executes CS requests in the increasing order of timestamps. • Every site Si keeps a queue, request_queuei , which contains mutex requests ordered by their timestamps. • This algorithm requires communication channels to deliver messages the FIFO order. 46

Lamport’s Mutex Algorithm • Requesting the CS – When a site Si wants to enter the CS, it broadcasts a REQUEST(tsi , i) message to all other sites and places the request on its own request_queuei. • tsi denotes the timestamp of the request from i. – When a site Sj receives the REQUEST(tsi, i) message from site Si, it places site Si’s request on its request_queuej and returns a timestamped REPLY message to Si. • Executing the CS – Site Si enters the CS when the following two conditions hold: • L 1: Si has received a REPLY message with timestamp larger than (tsi , i) from all other sites. • L 2: Si’s request is at the top of request_queuei. (lower timestamp request has higher priority) 47

Lamport’s Mutex Algorithm • Releasing the CS – Site Si, upon exiting the CS, removes its request from the top of its request queue and broadcasts a timestamped RELEASE message to all other sites. – When a site Sj receives a RELEASE message from site Si, it removes Si’s request from its request queue (Sj ‘s request is the next) • When a site removes a request from its request queue, its own request may come at the top of the queue, enabling it to enter the CS. • When a site receives a REQUEST, REPLY, or RELEASE message, it updates its clock using the timestamp in the message. – The following figures illustrates the operation of Lamport’s mutex algorithm on three sites S 1, S 2, and S 3. 48

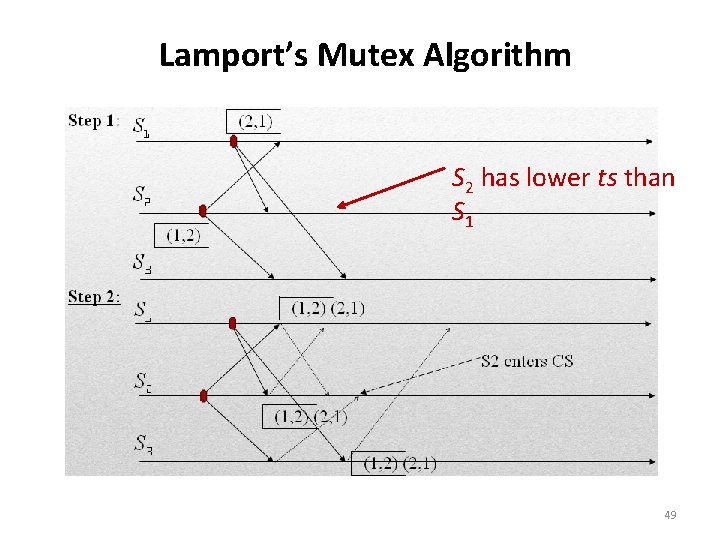
Lamport’s Mutex Algorithm S 2 has lower ts than S 1 49

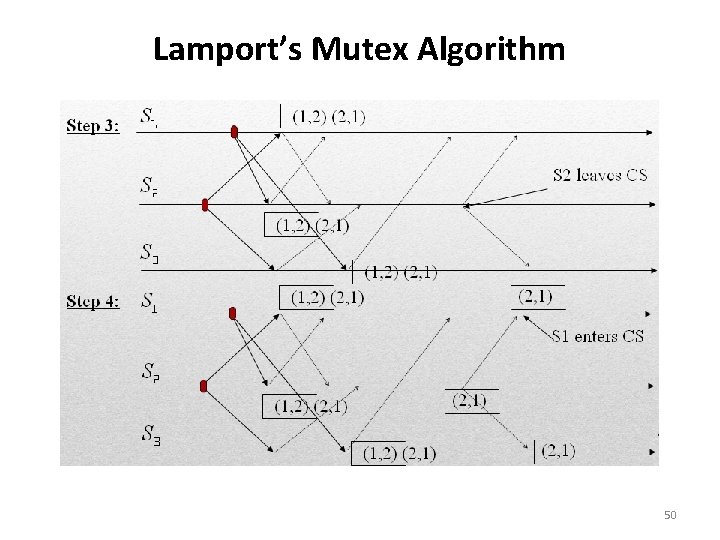
Lamport’s Mutex Algorithm 50

Correctness of Lamport’s Mutex Algorithm • Theorem 9. 1 Lamport’s algorithm achieves mutual exclusion. – Proof: • The proof is by contradiction. Suppose a site Si’s request has a smaller timestamp than the request of another site Sj and Sj is able to execute the CS before Si. • For Sj to execute the CS, it has to satisfy the conditions L 1 and L 2. This implies that at some instant in time say t, Sj has its own request at the top of its queue and it has also received a message with timestamp larger than the timestamp of its request from all other sites. • But request queue at a site is ordered by timestamp, and according to our assumption Si has lower timestamp. So Si ’s request must be placed ahead of the Sj ’s request in the request_queuej. This is a contradiction! 51

Performance of Lamport’s Mutex Algorithm • For each CS execution, Lamport’s algorithm requires (N − 1) REQUEST messages, (N − 1) REPLY messages, and (N − 1) RELEASE messages. • Thus, Lamport’s algorithm requires 3(N − 1) messages per CS invocation. • Synchronization delay in the algorithm is T. 52

Lamport’s Algorithm - Summary Nodal properties Every process maintains a queue of pending requests for entering CS ordered according Requesting process • • • Enters its request in its own queue Sends a request to every node Wait for replies from all other nodes If own request is at the head of the queue and all replies have been received, enter CS Upon exiting the CS, send a release message to every process Other processes • • • After receiving a request, send a reply and enter the request in the request queue After receiving release message, remove the corresponding request from the request queue If own request is at the head of the queue and all replies have been received, enter CS Message complexity • This algorithm creates 3(N − 1) messages per request Drawbacks • There exist multiple points of failure 53

Optimization of Lamport’s Mutex Algorithm • In Lamport’s algorithm, REPLY messages can be omitted in certain situations. – For example, if site Sj receives a REQUEST message from site Si after it has sent its own REQUEST message with timestamp higher than the timestamp of site Si ’s request, then site Sj need not send a REPLY message to site Si. – This is because when site Si receives site Sj ’s request with timestamp higher than its own, it can conclude that site Sj does not have any smaller timestamp request which is still pending. – With this optimization, Lamport’s algorithm requires between 3(N − 1) and 2(N − 1) messages per CS execution. 54

Ricart–Agrawala Mutex Algorithm • The Ricart-Agrawala algorithm assumes the communication channels are FIFO. • The algorithm uses two types of messages: REQUEST and REPLY. • A process sends a REQUEST message to all other processes to request their permission to enter the CS. • A process sends a REPLY message to a process to give its permission to that process. • Processes use Lamport-style logical clocks to assign a timestamp to CS requests and timestamps are used to decide the priority of requests. • Each process pi maintains the Request-Deferred array, RDi , the size of which is the same as the number of processes in the system. • Initially, ∀i ∀j : RDi [j]= 0. Whenever pi defer the request sent by pj, it sets RDi [j]=1 and after it has sent a REPLY message to pj, it sets RDi [j]= 0. 55

Ricart–Agrawala Mutex Algorithm 56

Ricart–Agrawala Mutex Algorithm – When a site receives a message, it updates its clock using the timestamp in the message. – When a site takes up a request for the CS for processing, it updates its local clock and assigns a timestamp to the request. – In this algorithm, a site’s REPLY messages are blocked only by sites that are requesting the CS with higher priority (i. e. , smaller timestamp). – When a site sends out deferred REPLY messages, the site with the next highest priority request receives the last needed REPLY message and enters the CS. • Execution of the CS requests in this algorithm is always in the order of their timestamps. 57

Ricart–Agrawala Mutex Algorithm • Figures 9. 7 to 9. 10 illustrate the operation of the Ricart– Agrawala algorithm. • In Figure 9. 7, sites S 1 and S 2 are each making requests for the CS and sending out REQUEST messages to other sites. The timestamps of the requests are (2, 1) and (1, 2), respectively. • In Figure 9. 8, S 2 has received REPLY messages from all other sites and, consequently, enters the CS. • In Figure 9. 9, S 2 exits the CS and sends a REPLY message to site S 1. • In Figure 9. 10, site S 1 has received REPLY from all other sites and enters the CS next. 58

Ricart–Agrawala Mutex Algorithm 59

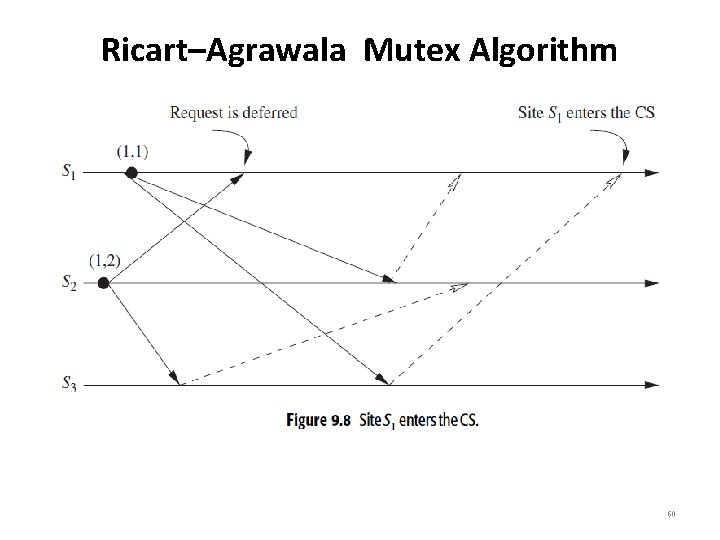
Ricart–Agrawala Mutex Algorithm 60

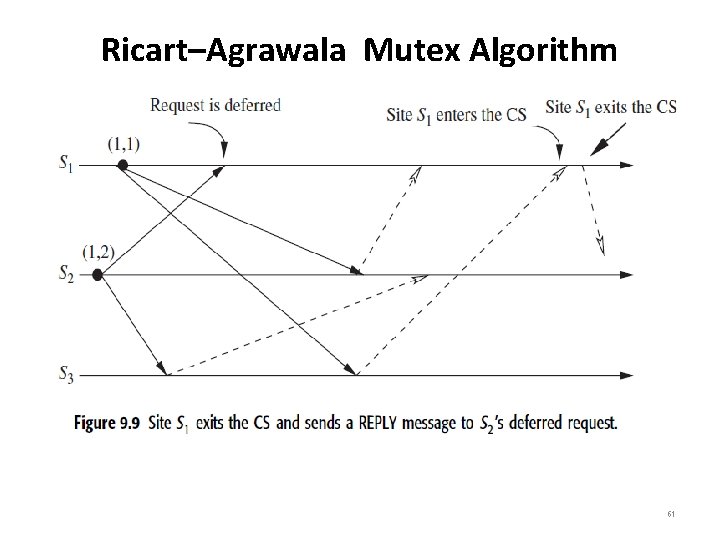
Ricart–Agrawala Mutex Algorithm 61

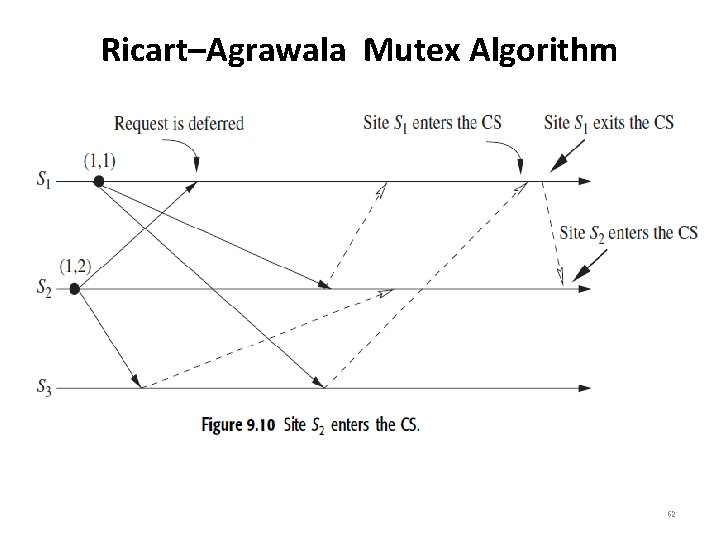
Ricart–Agrawala Mutex Algorithm 62

Ricart–Agrawala Mutex Algorithm Dr. K. G Anilkumar 63

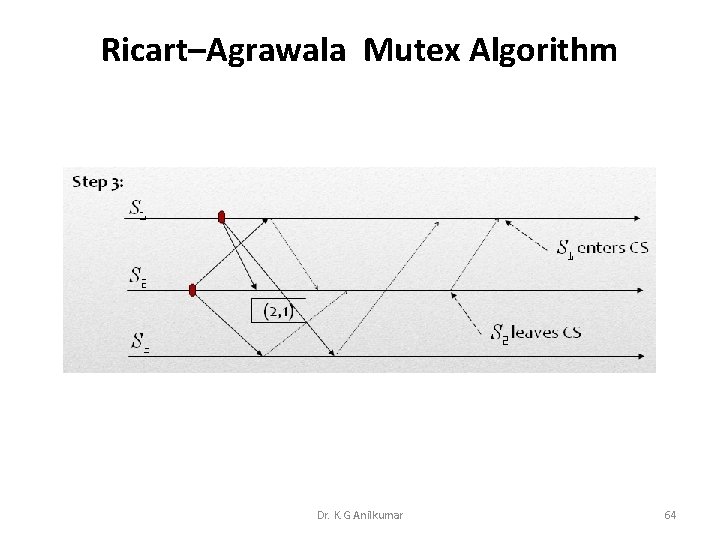
Ricart–Agrawala Mutex Algorithm Dr. K. G Anilkumar 64

Correctness of Ricart–Agrawala Mutex Algorithm 65

Performance of Ricart–Agrawala Mutex Algorithm 66

Summary - The Ricart-Agrawala Algorithm Terminology – The requesting site is the site which is requesting entry into the CS – The receiving site is every other site which is receiving the request from the requesting site. Requesting Site: Sends a message to all sites. This message includes the site's name, and the current timestamp of the system according to its logical clock Receiving Site: Upon reception of a request message, immediately send a timestamped reply message if and only if : – the receiving process is not currently interested in the CS OR – the receiving process has a lower priority Otherwise, the receiving process will defer the reply message. This means that a reply will be sent only after the receiving process has finished using the CS itself CS Execution: • Requesting site enters its CS only after receiving all reply messages • Upon exiting the CS, the site sends all deferred reply messages Performance • Number of network messages; 2*(N-1) • Synchronization Delays: One message propagation delay Problem: • One of the problems in this algorithm is failure of a node. In such a situation a process may starve forever 67

Token-based Mutex Algorithms • In token-based algorithms, a unique token is shared among the sites. • A site is allowed to enter its CS if it possesses the token. • A site holding the token can enter its CS repeatedly until it sends the token to some other site. – Depending upon the way a site carries out the search for the token, there are numerous token-based algorithms existing. • Token-based algorithms use sequence numbers instead of timestamps (used to distinguish between old and current token requests. ) 68

Suzuki–Kasami’s Broadcast Algorithm • If a site wants to enter the CS and it does not have the token, it broadcasts a REQUEST message for the token to all other sites. • A site which possesses the token sends it to the requesting site upon the receipt of its REQUEST message. • If a site receives a REQUEST message when it is executing the CS, it sends the token only after it has completed the execution of the CS. 69

Suzuki–Kasami’s Broadcast Algorithm • This algorithm efficiently addresses the following two design issues: – How to distinguish an outdated REQUEST token message from a current REQUEST message? • Due to message delays, a site may receive a token request message after the corresponding request has been satisfied. – How to determine which site has an outstanding request for the CS? • After a site has finished the execution of the CS, it must determine what sites have an outstanding request for the CS so that the token can be dispatched to one of them. 70

Suzuki–Kasami’s Broadcast Algorithm • The first issue is addressed in the following manner: – A REQUEST message of site Sj has the form REQUEST(j, n) where (n =1, 2, …) is a sequence number which indicates that site Sj is requesting its nth CS execution. – A site Si keeps an array of integers RNi[1. . N] where RNi [j] denotes the largest sequence number received in a REQUEST message so far from site Sj. – When site Si receives a REQUEST(j, n) message, it sets RNi [j] : = max(RNi [j], n). – When a site Si receives a REQUEST(j, n) message, the request is outdated if RNi [j] > n. 71

Suzuki–Kasami’s Broadcast Algorithm • The second issue is addressed in the following manner: – The token consists of a queue of requesting sites, Q, and an array of integers LN[1. . N], where LN[j] is the sequence number of the request which site Sj executed most recently. – After executing its CS, a site Si updates LN[i]: =RNi [i] to indicate that its request corresponding to sequence number RNi [i] has been executed. – At site Si if RNi [j] =LN[j]+1, then site Sj is currently requesting token. 72

Suzuki–Kasami’s Broadcast Algorithm 73

Suzuki–Kasami’s Broadcast Algorithm Correctness 74

Suzuki–Kasami’s Broadcast Algorithm Performance 75